Основой спектрального анализа сигналов является представление функции времени в виде ряда или интеграла Фурье. Любой периодический сигнал s(t), удовлетворяющий условию Дирихле, может быть представлен в виде ряда по тригонометрическим функциям

(2.63)

где ,

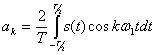(2.64)

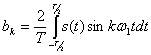(2.65)

Величина , выражающая среднее значение сигнала за период, называется постоянной составляющей. Она вычисляется по формуле

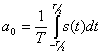(2.66)

Весьма удобной является комплексная форма записи ряда Фурье

(2.67)

где

,

Величина A есть комплексная амплитуда, она находится по формуле

A 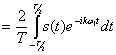(2.68)

Соотношения (2.67) и (2.68) составляют пару дискретных, преобразований Фурье. Необходимо отметить, что рядом Фурье можно представить не только периодический сигнал, но и любой сигнал конечной длительности. В последнем случае сигнал s(t) принимается периодически продолженным на всей оси времени. При этом равенство (2.63) или (2.67) представляет сигнал только на интервале его длительности (-T/2, T/2). Случайный сигнал (или помеха), заданный на интервале (-T/2, T/2), может быть также представлен рядом Фурье

(2.69)

где и являются случайными величинами (для флуктуационной помехой — независимыми случайными величинами с нормальным распределением). Тригонометрические функции

являются ортогональными на интервале (-T/2, T/2), но не являются нормированными. Ортонормированными будут следующие функции:

Учитывая это, обычный ряд Фурье (2.63) удобно записать в виде:

(2.70)

(2.71)

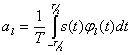
Коэффициенты в разложении (2.70) представляют собой эффективные значения составляющих спектра сигнала. Средняя мощность сигнала, выделяемая на сопротивлении 1 Ом,

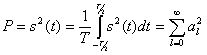(2.72)

Флуктуационную помеху ω(t) с постоянной интенсивностью также удобно представить рядом Фурье в форме, аналогичной (2.70):

(2.73)

где ξ — случайная величина, имеющая нормальное распределение вероятностей с нулевым средним значением и единичной дисперсией. Если сигнал ограничен полосой F, то ряд Фурье превращается в конечную тригонометрическую сумму

(2.74)

Число слагаемых, определяющих такой сигнал, равно его базе v=2TF, где — условная полоса частот, занимаемая сигналом.

Практически ширина спектра сигнала обычно определяется как область частот, в пределах которой сосредоточена основная энергия сигнала (например, 95%). Иногда эту полосу определяют также с учетом требования сохранения формы сигнала. Хотя условия одновременного ограничения длительности и полосы частот не могут быть выполнены в точности, однако можно ограничить спектр полосой F и иметь малые значения сигнала вне интервала Т.

Непериодический сигнал можно рассматривать как периодический с периодом . При этом разность частот между соседними гармониками стремится к нулю. Спектр становится сплошным, амплитуды — бесконечно малыми. Путем предельного перехода для представления непериодического сигнала получим интегральную пару преобразований Фурье:

(2.75)

,

Где S(iω)— спектральная плотность сигнала. Поскольку спектральная характеристика S(iω)— комплексная величина, то ее можно представить в виде

S(iω)=А(ω)+iВ(ω)=S(ω)е (2.76)

,

Модуль и фаза спектральной характеристики соответственно равны:

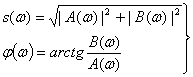(2.77)

Структура спектра непериодического сигнала полностью определяется функциями частоты S(ω) (спектром амплитуд) и φ(ω) (спектром фаз).

Для примера определим спектр колокольного импульса. Этот импульс выражается функцией

(2.78)

Замечательным свойством этой функции является ее инвариантность при преобразовании Фурье: спектр колокольного импульса представляет coбoй также колокольную кривую. Действительно, для спектра импульса (2.78) получаем

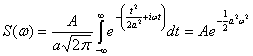(2.79)

Графики пары преобразований (2.78) и (2.79) приведены на рис. 2.7а и б.

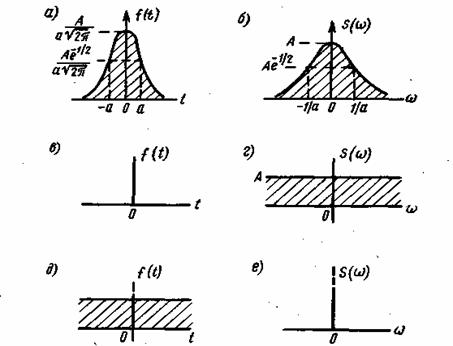
Рис. 2.7. Колокольный импульс и его предельные формы

Изменение параметра а на кривых этого рисунка показывает, что короткий импульс имеет широкий спектр, а длинный импульс — узкий спектр. Это свойство относится не только к данному примеру. Оно является общим положением, согласно которому ширина спектра любого процесса обратно пропорциональна его длительности. На рис. 2.7 в и г показаны предельные формы колокольных функций рис. 2.7а и б при малом параметре а. Здесь при а0 импульс вырождается в дельта-функцию, спектр которой является равномерным. При возрастании параметров А и а, когда их отношение остается постоянным, импульс превращается в постоянный сигнал — сигнал нулевой частоты (рис. 2.7 д и е).