3.1. Аналитическое представление модулированных колебаний
3.2. Основные виды аналоговой модуляции
3.3. Сигналы при дискретной модуляции
3.4. Сигналы при импульсной модуляции
3.5. Энергетический спектр модулированных сигналов
3.1. Аналитическое представление модулированных колебаний
Модулированные сигналы различаются по виду переносчика (несущей) и по его модулированным параметрам. В качестве переносчиков в настоящее время широко используются гармонические колебания, периодическая последовательность импульсов и узкополосный случайный процесс. Каждый из этих переносчиков характеризуется определенным числом параметров. Параметры, изменяющиеся во времени под действием передаваемого сообщения, называются информационными, так как в их изменениях заложена передаваемая информация. Параметры, которые остаются неизменными, являются постоянными признаками сигнала; они могут быть использованы на приеме для отличения сигнала от помех. Во многих случаях модулированный сигнал можно представить как произведение двух функций
(3.1)
где 
— функция, представляющая несущее колебание (переносчик), а 
— модуляционная функция, выражающая воздействие передаваемого сообщения u(t) на несущую f(t). Когда для представления несущей выбирается аналитический сигнал (2.98), то для каждой модуляционной функции M(t) существует комплексный модулированный сигнал s(t). При аналитическом представлении сигнала его действительная и мнимая части соответствуют реально существующему модулированному сигналу, а его модуль определяет огибающую. В случае, когда несущей является гармоническое колебание 
, модуляционная функция выражает воздействие видеосигнала u(t) на амплитуду (частоту или фазу) несущей.
Спектр модулированного колебания (3.1) согласно теореме о спектре произведения определяется сверткой
(3.2)
Отсюда следует, что процесс модуляции приводит к сложному преобразованию спектра сигнала. Если несущая представляет собой узкополосное колебание, то модуляция приводит к расширению спектра и переносу его в область около несущей частоты (рис. 3.1 а). Если несущая — чистая синусоида, то имеет место простое смещение спектра (рис. 3.1 б). Если несущая записывается в форме аналитического сигнала, спектр которого существует только для положительных частот, то частотное преобразование относится только к положительным частотам, как показано на рис. 3.1.
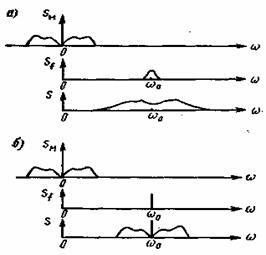
Рис. 3.1. Смещение спектра при модуляции: общий случай аналитической несущей (а), случай гармонической несущей (б)
3.2. Основные виды аналоговой модуляции
К основным видам аналоговой модуляции относятся амплитудная модуляция (AM), фазовая модуляция (ФМ) и частотная модуляция (ЧМ). Разновидностями AM являются балансная (БМ) и однополосная (ОМ) модуляции.
Непосредственная передача. Наиболее простым сигналом для передачи непрерывного сообщения u(t) является сигнал, пропорциональный u(t):
s(t)=Au(t), (3.3)
где А — некоторая постоянная. Такой сигнал соответствует форме (3.1), если в ней положить f(t)=A и М [u(t)]=u(t). Примером такой непосредственной передачи сообщений является обычная телефонная связь по проводам.
Амплитудная модуляция. Для этого вида модуляции: f(t)=,
где т — коэффициент модуляции.
Модулированный сигнал запишется
(3.4)
Это выражение даёт представление реального AM сигнала 
Спектр сигнала в общем случае определяется как преобразование Фурье от s(t):
Учитывая, что 
и 
получим
(3.5)
где 
— спектр передаваемого сообщения. Отсюда видно, что при AM происходит перенос спектра сообщения на частоту 
(рис. 3.16). Ширина спектра сигнала F при AM в два раза шире спектра сообщения Fm:
При модуляции одним тоном, когда
u(t)=
,
(3.6)
Из этого выражения следует, что амплитуда модулированного сигнала изменяется от 
до 
, а мощность сигнала соответственно от 
до 
Где 
мощность несущего колебания. Средняя мощность AM сигнала равна:
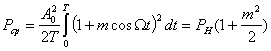
При m=l 
и Pcp=1,5PH; отношение средней мощности к максимальной равно 0,375. "Эти соотношения указывают на существенный недостаток амплитудной модуляции — плохое использование мощности передатчика.
Балансная модуляция (БМ). Кроме обычной AM применяется передача AM без несущей — балансная модуляция. Для этого вида модуляции:
f(t)=,
(3.7)
тогда
(3.8)
Спектр сигнала при БМ
(3.9)
Здесь имеются только две боковые полосы — несущая отсутствует.
При однополосной модуляции (ОМ) передается только одна боковая полоса. Для этого вида модуляции при передаче верхней боковой полосы:
f(t)=,
(3.10)
(3.11)
Спектр сигнала ОМ
(3.12)
Действительно, если разложить функции u(t) и 
(t) в ряд Фурье:
и учесть, что cosx; и sinx являются парой преобразования Гильберта, по получим
Такое представление является аналитическим для всех >0. Замена модуляционной функции [u(t)] на сопряженную ей *[u(t)]=u(t)-i
(t) дает форму сигнала s(t), соответствующую нижней боковой полосе.
Системы БМ и ОМ позволяют сократить бесполезный расход энергии на составляющую несущей частоты, а при ОМ дополнительно вдвое сократить ширину спектра передаваемого сигнала. Однако реализация указанных преимуществ требует более сложной аппаратуры.
Угловая модуляция. В случае угловой модуляции (ЧМ и ФМ) модуляционная функция имеет вид
(3.13)
При синусоидальной несущей f(t)=модулированный сигнал будет иметь следующее выражение:
(3.1 4)
Реальный сигнал
(3.15)
Это обычное представление сигнала с угловой модуляцией. Согласно (3.15) полная фаза высокочастотного колебания равна:
(3.16)
а мгновенная частота колебания изменяется по закону производной от 
, т. е.
(3.17)
Наоборот, при изменении частоты по закону ω(t) (3.17) фаза колебания ψ(t) будет изменяться по закону интеграла от ω(t):
(3.18)
В случае фазовой модуляции 
. Тогда на основании (3.15) и (3.16) имеем:
(З.19) 
(3.20)
При частотной модуляции по закону передаваемого сообщения изменяется частота несущего колебания
(3.21)
где
— амплитуда частотного отклонения (девиация частоты). Полная фаза колебания при этом будет равна:
(3.22)
Тогда выражение ЧМ сигнала запишется в виде
(3.23)
При модуляции одним тоном, когда и (t)=cosΩt, выражения сигнала при ФМ и ЧМ по форме имеют одинаковый вид:
(3.24)
где т — индекс модуляции: при ФМ 
при ЧМ 
Для определения спектра сигнала заменим в (3.24) косинус суммы двух углов по известным формулам из тригонометрии
(3.25)
Здесь для упрощения записи мы положим 
=0. Из теории бесселевых функций известны следующие соотношения:
(3.26)
(3.27)
где 
— бесселева функция первого рода k-гo порядка от аргумента т. После подстановки (3.26) и (3.27) в (3.25) получаем
(3.28)
Таким образом, оказывается, что даже при синусоидальных ЧМ и ФМ получается теоретически безграничный спектр. Он состоит из несущей ω0 и двух боковых полос 
. Амплитуда несущей А010(т) при ЧМ и ФМ. в отличие от AM, зависит от модулирующего колебания. При некоторых значениях т она может быть вообще равна нулю (т =2,3; 5,4). Амплитуда боковых частот равна 
. Однако практически ширина спектра ЧМ и ФМ сигналов ограничена.
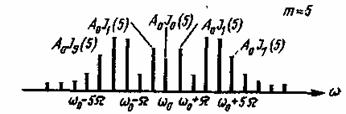
Рис. 3.2. Спектр сигнала с угловой модуляцией
На рис. 3.2 приведен спектр сигнала с угловой модуляцией одним тоном при m=5. Как видим, амплитуды боковых частот быстро убывают с увеличением номера гармоники k. При k>m составляющие спектра малы и ими можно пренебречь. Практически ширина спектра сигнала при угловой модуляции равна F=2(m+l)Fm, где Fт=
частота модулирующего колебания.
Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции Ω. При ЧМ т=
, поэтому при m>>1 полоса
практически не зависит от Fm. При ФМ b
при m>>1 ширина спектра будет равна F=2ΔφfmFm т. е. она зависит от модулирующей частоты Fm. В этом и состоит различие в спектрах ЧМ и ФМ.
В случае малого индекса модуляции спектр ЧМ и ФМ сигналов, так же как и в случае AM, имеет только три составляющие:
(3.29)
Это непосредственно следует из (3.28), если учесть, что при m<<l sin (msinΩt)
msinΩt, а cos (msinΩt)1.
Сравнение (3.6) и (3.29) показывает, что различие спектров сигналов при AM и угловой модуляции заключается только в сдвиге фазы колебания нижней боковой частоты на 180° относительно его положения при AM. Это различие существенно и иллюстрируется векторными диаграммами, изображенными на рис. 3.3.
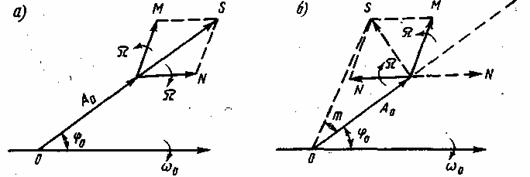
Рис. 3.3. Векторные диаграммы: AM сигнала (а), ЧМ сигнала (ш<1) (б)
Однополосная угловая модуляция. Если функция 
— аналитическая:
то сигнал
(3.30)
также является аналитической функцией при 
. Он не содержит отрицательных частот, хотя и имеет бесконечный спектр в области положительных частот:
(3.31)
Выражение (3.30) определяет новый модулированный сигнал. Этот сигнал представляет собой вариант сигнала однополосной угловой модуляции. Для доказательства этого рассмотрим случай частотной модуляции одним тоном u(t)=sinΩt. Для этого случая функция φ(t) и ее преобразование Гильберта принимают вид:
Где индекс модуляции. Модулирующая функция при этом преобразуется к виду
, а модулированный сигнал 
Отсюда видно, что спектр модулированного сигнала состоит из одной боковой полосы частот. Сигнал однополосной ЧМ можно получить из обычного ФМ сигнала путем преобразования Гильберта (например, посредством фазового сдвига на 
) и модуляции амплитуды по экспоненциальному закону. Тогда ограничение такого сигнала в приемнике восстановит нижнюю боковую полосу частот и позволит применить для детектирования обычный дискриминатор.
3.3. Сигналы при дискретной модуляции
При дискретной модуляции закодированное сообщение u(t), представляющее собой последовательность кодовых символов {
}, преобразовывается в последовательность элементов сигнала {
}. Последние отличаются от кодовых символов лишь электрическим представлением. В частном случае дискретная модуляция состоит в воздействии кодовых символов {аi} на переносчик f(t). Такая дискретная модуляция аналогична непрерывной.
Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление. Обычно же в качестве переносчика, как и при непрерывной модуляции, используется переменный ток (гармоническое колебание). В этом случае можно получить амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Дискретную модуляцию часто называют манипуляцией, а устройство, осуществляющее дискретную модуляцию (дискретный модулятор), называют манипулятором или генератором сигналов.
На рис. 3.4 приведены графики сигналов при различных видах манипуляции. При AM символу 1 соответствует передача несущего колебания в течение времени 
(посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой 
соответствует символу 1, а передача колебания 
соответствует 0. При ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1.
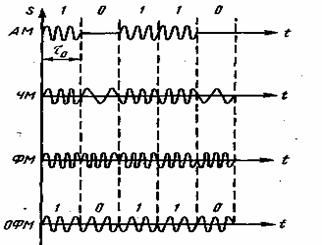
Рис. 3.4. Сигналы при различных видах дискретной модуляции
Наконец, в настоящее время применяется относительная фазовая модуляция (ОФМ). В отличие от ФМ, в системе ОФМ фаза несущего колебания изменяется на 180° при передаче символов 1 и остается неизменной при передаче символов 0.
При ОФМ манипуляция каждой данной посылки осуществляется относительно предыдущей. Очевидно, таким способом можно манипулировать (изменять) любой параметр несущего колебания: при изменении частоты получим относительную частотную манипуляцию (ОЧМ), при изменении амплитуды относительную амплитудную манипуляцию (ОАМ). Дельта-модуляция, о которой мы упоминали в § 1.6, также является одним из видов относительной манипуляции.
Рассмотрим спектры сигналов при некоторых видах дискретной модуляции. Будем полагать, что модуляция производится двоичным сообщением u(t), представляющим собой периодическую последовательность прямоугольных импульсов с периодом 
.
Амплитудная манипуляция. Сигнал AM можно записать в виде
(3.32)
где периодическая функция u(t) на интервале равна:
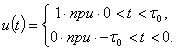(3.33)
Представим u(t) рядом Фурье
(3.34)
Тогда сигнал AM запишется в виде
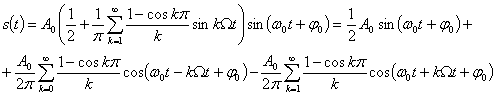(3.35)
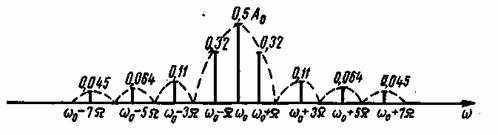
Рис. 3.5. Спектр сигнала при амплитудной манипуляции
Спектр сигнала AM, построенный по ф-лам (3.35), показан на рис. 3.5. Он состоит из несущего колебания с амплитудой 
и двух боковых полос, спектральные составляющие которых имеют амплитуды
(3.36)
Огибающая спектра дискретного сигнала AM выражается формулой
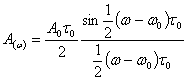(3.37)
т. е. представляет собой смещенный на частоту спектр одиночного импульсного сигнала u(t).
Фазовая манипуляция. Сигнал ФМ можно записать в виде
(3.38)
Периодическая функция, определяющая закон изменения фазы на интервале , выражается формулой
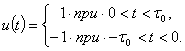(3.39)
Подстановка (3.39) в выражение (3.38) дает
Представим u(t) рядом Фурье
Тогда сигнал ФМ запишется в виде
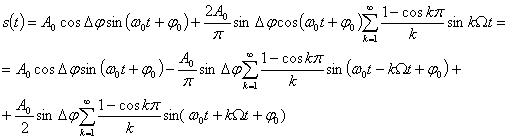(3.40)
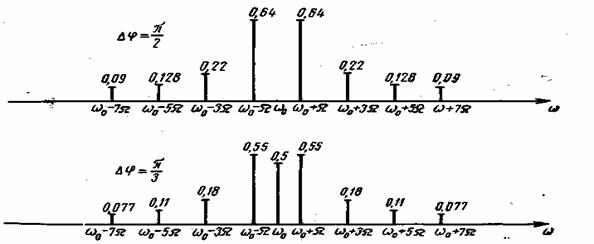
Рис. 3.6. Спектры сигналов при фазовой манипуляции
Спектр сигнала ФМ для различных значений девиаций фазы 
, построенной на основании ф-лы (3.40), показан на рис. 3.6. Он состоит из несущего колебания и двух боковых полос. Амплитуда несущего колебания зависит от : 
и при =
— обращается в 0. Амплитуды спектральных составляющих в боковых полосах также зависят от . При увеличении от 0 до , как видно из рис. 3.6, амплитуда несущего колебания убывает до нуля, а амплитуды боковых частот увеличиваются.
Когда =— вся энергия сигнала ФМ содержится только в боковых полосах. Так же, как и при AM, огибающая дискретного спектра боковых частот представляет собой смещенный на частоту спектр одиночного импульсного сигнала u(t), умноженный нa sin:
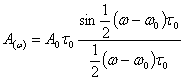(3.41)
Аналогично определяется спектр сигнала при частотной манипуляция.
3.4. Сигналы при импульсной модуляции
В системах связи с импульсной модуляцией переносчиком Информации служит периодическая последовательность импульсов одинаковой формы
(3.42)
где U(t) — нормированная функция, характеризующая форму импульса; A0 — амплитуда импульса; 
— начало переднего фронта k-го импульса 
;
— период следования импульсов; 
— начало отсчета последовательности; 
— длительность k-го импульса, отсчитываемая на некотором заданном уровне.
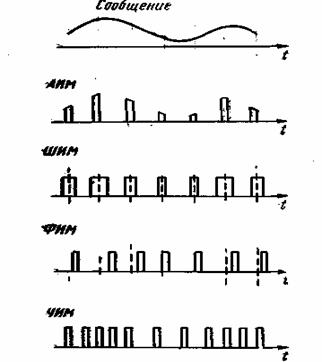
3.7. Сигналы при различных видах импульсной модуляции
При модуляции один из параметров последовательности изменяется в соответствии с передаваемым сообщением (рис. 3.7). Так, при амплитудно-импульсной модуляции (АИМ) изменяется амплитуда импульса А:
(3.43)
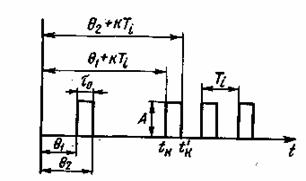
Рис. 3.8. Параметры периодической последовательности прямоугольных импульсов
При широтно-импульсной модуляции (ШИМ) изменяется длительность импульса
(3.44)
где 
— максимальное отклонение фронта импульсов в одну сторону.
При фазовой импульсной модуляции (ФИМ) изменяется сдвиг импульсов относительно тактовых точек 
.
(3.45)
При частотно-импульсной модуляции (ЧИМ) в соответствии с передаваемым сообщением изменяется частота следования импульсов.
Так же, как и при ФИМ, импульсы сдвигаются относительно тактовых точек, но в другой закономерности. Различие между ФИМ и ЧИМ аналогично различию между ФМ и ЧМ синусоидального переносчика.
Периодическую последовательность прямоугольных импульсов (рис. 3.8) можно записать в следующем виде:
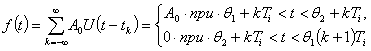(3.46)
Такую последовательность импульсов можно представить рядом Фурье. В соответствии с выражениями (2.67) и (2.68) имеем
,где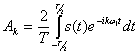 
,
В нашем случае
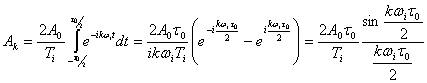(3.47)
тогда
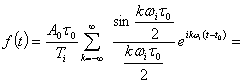
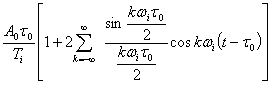(3.48)
где 
2я
Спектр амплитуд периодической последовательности прямоугольных импульсов приведен на рис. 3.9. Амплитуды спектральных компонент 
определяются значениями модуля спектральной плотности || (3.47) на гармониках частоты повторения 
.Форма огибающей частотного спектра периодической последовательности определяется формой отдельного импульса. С увеличением периода повторения интервал частот между соседними спектральными компонентами сокращается, их число растет, а амплитуда каждой компоненты уменьшается при сохранении постоянного соотношения между ними. При неограниченном увеличении периодическая последовательность вырождается в одиночный импульс, а линейчатый спектр становится сплошным.
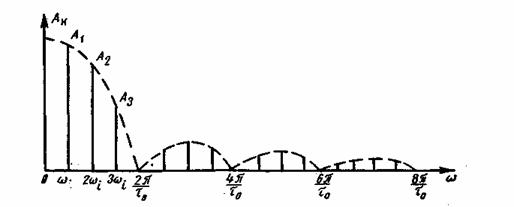
Рис. 3.9. Спектр периодической последовательности прямоугольных импульсов
Спектр периодической последовательности радиоимпульсов получается из спектра последовательности видеоимпульсов переносом шкалы частот на несущую частоту и дополнением полученного спектра его зеркальным отображением.
При модуляции параметры, входящие в выражения (3.46) и (3.48), являются функциями времени:
. Модулированная последовательность будет представлять теперь уже непериодическую функцию, деформированную относительно исходной:
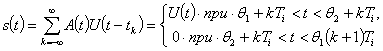(3.49)
или согласно (3.48)
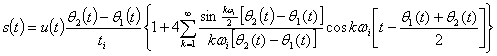(3.50)
Полученная формула определяет частотный спектр деформированной последовательности импульсов. Для получения спектров сигналов при различных видах модуляции в ф-лу (3.50) необходимо подставить соответствующее выражение модулированного параметра.
Для примера найдем спектр при АИМ. При модуляции одним тоном u(t)=sinΩ(t) и A=A0(1+msinΩt); остальные параметры последовательности неизменны: 
После подстановки этих значений в (3.50) и несложных тригонометрических преобразований для частотного спектра АИМ сигнала получаем
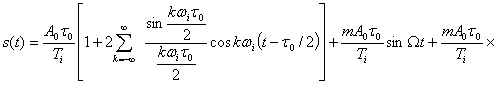
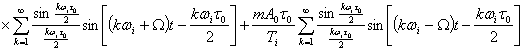(3.51)
На рис. 3.10 приведен график спектра АИМ сигнала. Сравнение его с рис. 3.9 показывает, что при АИМ модулируется по амплитуде каждая составляющая спектра немодулированной последовательности импульсов как изолированная «несущая». В спектре содержится низкочастотное модулирующее сообщение u(t) с частотой Ω, следовательно, демодуляция при АИМ может быть осуществлена с помощью фильтра нижних частот, пропускающего низкочастотное колебание u(t).
Аналогично определяется спектр и для других видов импульсной модуляции. Для вычисления спектра при ФИМ в (3.50) необходимо подставить выражение (3.45), определяющее изменение положения импульса в соответствии с передаваемым сообщением, а при ШИМ — выражение (3.44), определяющее изменение длительности импульса.
При импульсно-кодовой модуляции (ИКМ) передача отдельных значений сигнала сводится к передаче определенных групп импульсов. Эти группы передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов. Каждая кодовая группа импульсов представляет собой регулярный непериодический сигнал, спектр которого может быть вычислен на основании преобразований Фурье обычным образом.
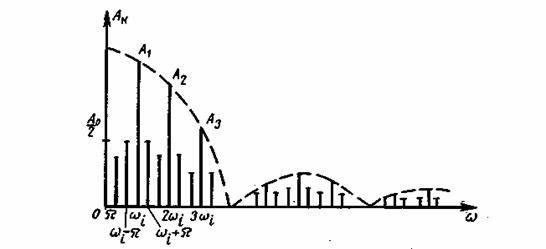
Рис. 3.10. Спектр АИМ сигнала
Ширина спектра последовательности импульсов практически не зависит от частоты повторения 
и определяется, главным образом, шириной спектра одного импульса. При наличии модуляции любого вида спектр расширяется незначительно за счет боковых частот крайних составляющих спектра немодулированных импульсов. Поэтому рабочая полоса частот, занимаемая импульсными сигналами, практически не зависит от вида модуляции и определяется длительностью и формой импульса.
3.5. Энергетический спектр модулированных сигналов
До сих пор мы рассматривали модуляцию несущего колебания детерминированным процессом u(t), который отображает определенное сообщение или отдельную его реализацию. Совокупность же возможных сообщений представляет собой некоторый случайный процесс. Так, при передаче речи или музыки статистические свойства передаваемых сообщений очень близки к свойствам нормального случайного процесса. Важнейшими характеристиками колебания, модулированного случайным процессом, являются функция корреляции и энергетический спектр.
Следует подчеркнуть, что модулированный сигнал является нестационарным случайным процессом даже тогда, когда модулирующие процессы (сообщения) стационарны. Энергетический спектр нестационарного случайного процесса определяется посредством двукратного усреднения — по множеству и по времени. Сначала определяется усредненная по времени корреляционная функция, а затем обратным преобразованием Фурье — искомый энергетический спектр.
Рассмотрим случай, когда передаваемое сообщение u(t) представляет собой стационарный процесс с u(t)=0, а переносчик — гармоническое колебание 
.
При амплитудной модуляции
s(t) = А0[1 + ти(t)]cos ω0t,
где m — среднеквадратическое значение коэффициента модуляции. Функция корреляции модулированного сигнала
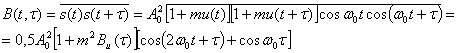
где Bu(t) — функция корреляции передаваемого сообщения u(t). Как видим, функция B(t, τ) зависит от времени, что указывает на нестационарность модулированного сигнала. После усреднения по времени получаем
(3.52)
Применяя к В (τ) преобразование Фурье (2.84), находим энергетический спектр сигнала при AM
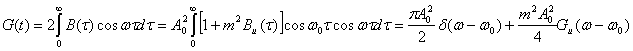
Таким образом, спектр модулированного по амплитуде гармонического колебания случайным процессом состоит из несущего колебания с частотой и смещенного на спектра передаваемого сообщения u(t).
Сигнал при угловой модуляции (ЧМ и ФМ) можно записать в общем виде
s(t) = А0cos 
,
При ФМ 
, а при ЧМ.
Здесь 
и 
— среднеквадратические значения девиации соответственно фазы и частоты.
Функция корреляции модулированного сигнала
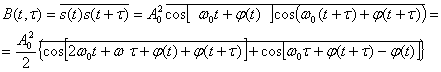
При усреднении по времени первое слагаемое обращается в нуль. Второе слагаемое не зависит от времени t поэтому
Обозначим разность 
и по известной формуле представим косинус суммы двух углов в виде
Средние по множеству значения косинуса и синуса 
можно найти, если известен закон распределения вероятностей сообщения u(t). Если u(t) подчиняется нормальному закону, то 
, являющееся линейным преобразованием от u(t), также будет иметь нормальное распределение с нулевым средним значением и дисперсией 
. Легко убедиться, что в этом случае:
Таким образом, усредненная по времени функция корреляции сигнала при угловой модуляции
(3.54)
Дисперсию процесса можно выразить через функцию корреляции или энергетический спектр сообщения u(t). Действительно.
(3.55)
где 
— функция корреляции процесса . При 
, поэтому 
; при ЧМ 
, где 
, поэтому 
. Далее можно определить энергетический спектр модулированного сигнала путем преобразования Фурье (2.81) от функции 
(3.54).
3.6. Модуляция шумовой несущей
В качестве переносчика можно использовать не только периодические колебания, но и узкополосный случайный процесс. Такие переносчики также находят практическое применение. Например, в оптических системах связи, в которых используется некогерентное излучение, сигнал, по существу, представляет собой узкополосный гауссов шум.
Согласно (2.36) узкополосный случайный процесс можно представить как квазигармоническое колебание
с медленно изменяющимися огибающей 
и фазой 
. При амплитудной модуляции в соответствии с передаваемым сообщением изменяется огибающая U(t), при фазовой модуляции — фаза и при частотной — мгновенная частота 
.
Рассмотрим амплитудную модуляцию шумовой несущей. Выражение для модулированной несущей в этом случае можно записать в виде
y(t) = [1 + ти(t)]f(t), (3.57)
где f(t) — переносчик, u(t) — модулирующая функция (видеосигнал), m — коэффициент модуляции.
Предполагается, что модулирующий процесс u(t) также представляет собой стационарный нормальный процесс со средним значением, равным нулю u(t) = 0. Процессы f(t) и u(t) независимы. При этих ограничениях функция корреляции модулированной по амплитуде шумовой несущей будет
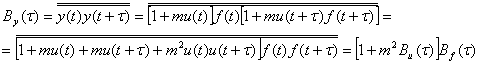(3.58)
Теперь находим энергетический спектр
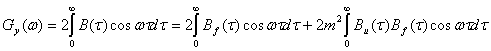
Первый интеграл дает энергетический спектр шумовой несущей 
. Для второго интеграла на основании теоремы о спектре произведения имеем
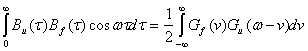
Окончательно спектр модулированной несущей будет равен:
(3.59)
Таким образом, спектр модулированной по амплитуде шумовой несущей получается суперпозицией спектра несущей и свертки этого спектра со спектром передаваемого сообщения, сдвинутого в область высоких частот на величину .Аналогично определяются функция корреляции и энергетический спектр при ФМ и ЧМ.
Применение «шумовых» сигналов позволяет ослабить влияние замираний в каналах с многолучевым распространением радиоволн. Поясним это на простейшем примере. Пусть на вход приемника поступают сигналы двух лучей 
и 
сдвигом на τ. время т. Мощность результирующего сигнала, определяемая за достаточно большое время Т,
где
— функция корреляции сигнала, Р0— его средняя мощность. Функция корреляции шума быстро убывает с увеличением т и тем быстрее, чем шире его спектр. Следовательно, при достаточно большой ширине спектра можно считать 0 и 
, т. е. средняя мощность принятого сигнала, несмотря на замирания, остается примерно постоянной.
3.7. Шумоподобные сигналы
Применение в качестве переносчика реализаций реального шума связано с определенными трудностями, которые возникают при формировании и приеме таких сигналов. Поэтому на практике нашли применение шумоподобные сигналы. Эти сигналы не являются случайными. Они формируются по определенному алгоритму. Однако их статистические свойства близки к свойствам шума: энергетический спектр почти равномерный, а функция корреляции имеет узкий основной пик и небольшие боковые выбросы. Шумоподобные и шумовые сигналы относятся к типу широкополосных сигналов (TF>>1).
В настоящее время известны методы формирования шумоподобных сигналов, которые при большой базе 2TF позволяют независимо воспроизводить их на приемном и передающем концах и отвечают требованиям синхронизации этих сигналов.
Широкое применение находят дискретные сигналы, которые строятся следующим образом. Информационная посылка длительностью Т разбивается на N бинарных элементов длительностью 
(рис. 3.11). Такое разбиение позволяет получить сигнал длительностью Т с полосой 
— и значением базы 2TF
. Последовательности бинарных элементов образуют коды, которые выбираются так, чтобы обеспечить заданные свойства сигнала. С помощью модуляции или гетеродинирования формируется высокочастотный сигнал, который передается по каналу. Часто при этом используется модуляция фазы на два положения: 0 и π
Функция корреляции дискретных сигналов при достаточно большом значении числа элементов N имеет главный максимум, сосредоточенный в области 
, и боковые лепестки, имеющие сравнительно малый уровень (рис. 3.11). Эта функция сильно напоминает функцию автокорреляции отрезка шума с полосой F. Отсюда и произошло название шумоподобные сигналы.
В системах связи, в которых используются шумоподобные (составные) сигналы, каждый элемент сообщения передается не одним, а несколькими элементами сигнала, несущими (повторяющими) одну и ту же информацию. Число N может достигать нескольких сотен и даже тысяч. Как будет показано в дальнейшем, это позволяет реализовать накопление сигнала, обеспечивающее высокую помехоустойчивость даже в том случае, когда уровень сигнала ниже уровня помех.
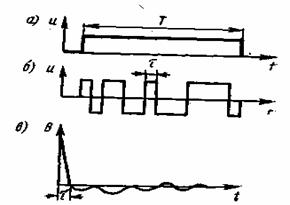
Рис. 3.11. Принцип построения сложного широкополосного сигнала
Обширный класс дискретных сигналов строится на основе линейных рекуррентных последовательностей. Эти сигналы имеют хорошие корреляционные свойства и сравнительно несложную практическую реализацию. Структура сигналов имеет случайный характер, хотя способ их формирования вполне регулярен. Непрерывные ФМ сигналы, построенные на основе рекуррентных последовательностей, могут иметь почти идеальную автокорреляционную функцию.
Среди линейных рекуррентных последовательностей особое место занимают псевдослучайные М-последовательности Хаффмена. Они представляют собой совокупность N периодически повторяющихся символов 
, каждый из которых может принимать одно из двух значений: +1 или -1. Это значение определяется взятым с противоположным знаком произведением значений двух или большего числа (но всегда четного) предыдущих сигналов
(3.60)
причем 
;.
Если выбрать исходную последовательность 
, то на основании (3.60) можно образовать неповторяющуюся элементарную последовательность {d
} из N символов, где
(3.61)
Она будет содержать все комбинации п символов из двух элементов: +1 и -1, кроме комбинаций, состоящих из одних отрицательных единиц. Вследствие этого каждая последовательность {d} coдержит 
положительных единиц и 
отрицательных единиц. Поэтому
(3.62)
При 
символы повторяются в том же порядке, т. е. при любом целом
di+pN = dl (3.63)
Рассмотрим простейший пример: n=2. В этом случае 
. Выберем исходную последовательность 
тогда 
и т. д. Отсюда искомая последовательность будет: ... -1, +1, +1, -1, +1, +1, -1, +1,+1,... Она содержит все возможные комбинации из двух символов: -1, +1; +1, +1; +1, -1, кроме запрещенной комбинации -1, -1. Полученная последовательность -1, +1, +1 повторяется через 
символа. При п=3 можно образовать две последовательности из 
символов по правилам 
и 
. Почти каждому целому числу п соответствует несколько чисел k, при которых по правилу (3.60) образуется последовательность.
Из выражения (3.63) следует, что число N является максимальным периодом бесконечной последовательности Хаффмена. Могут образоваться также последовательности меньшего периода. Максимальное число различных последовательностей максимального периода для любого п равно:
(3.64)
где 
— функция Эйлера.
Бинарные псевдослучайные последовательности Хаффмена обладают рядом замечательных свойств. Нормированная функция автокорреляции в непрерывном режиме работы имеет главный максимум, равный единице, и одинаковые по величине боковые лепестки, равные 
. Функция взаимной корреляции для различных последовательностей равна -1/М. В импульсном режиме работы уровень боковых лепестков не превышает величины 
. Различные последовательности при заданном п отличаются как порядком чередования символов +1 и -1, так и максимальным значением боковых лепестков. При этом можно указать последовательность, у которой максимальный уровень боковых лепестков будет наименьшим среди возможных последовательностей для заданного п. Генерирование псевдослучайных последовательностей Хаффмена сравнительно просто осуществляется с помощью регистров сдвига.
Кроме сигналов Хаффмена, практическое применение находят и другие виды дискретных сигналов. Можно указать сигналы ПэлиПлоткина, последовательность символов Лежандра, коды Баркера, многофазные коды Фрэнка [9]. Возможны, наконец, различные варианты составных сигналов.
В радиолокации широко применяются сигналы с линейным изменением частоты внутри импульса (ЛЧМ). Объясняется это тем, что сигналы ЛЧМ имеют хорошие корреляционные свойства и прием их легко может быть осуществлен с помощью согласованных фильтров.
Шумоподобный сигнал может подвергаться всем известным способам модуляции. При амплитудной модуляции изменяются амплитуды всех его элементов. При частотной модуляции варианты сигнала отличаются средней частотой, при фазовой — разностью фаз между элементами двух посылок.
Специфическим видом модуляции, свойственным только широкополосным системам связи, является структурная модуляция или модуляция по форме сигнала. В этом случае в качестве вариантов сигнала используются колебания, построенные из одинаковых элементов, но с разным взаимным расположением этих элементов. Например, двоичную передачу можно осуществить с помощью сигналов вида:
(3.65)
где 
и 
— функции, принимающие значения ±1 в соответствии с заданной кодовой последовательностью и удовлетворяющие условию
При выполнении последнего условия имеем систему почти ортогональных сигналов. В качестве функций и , удовлетворяющих условию (3.66), можно использовать рассмотренную выше двоичную псевдослучайную последовательность Хаффмена =
и эту же последовательность со сдвигом во времени =
Аналогично строятся многопозиционные широкополосные системы со структурной модуляцией. В этом случае используется ансамбль шумополобных сигналов 
. При этом, конечно, различие между этими сигналами должно быть достаточным для их разделения на приеме. С этой точки зрения большой интерес представляют противоположные и ортогональные сигналы.
Вопросы для повторения
1. Изобразите векторные диаграммы AM и ЧМ сигналов.
2. Определите среднюю мощность AM сигнала.
3. При каком виде модуляции ширина спектра сигнала минимальна? Чему она равна? Чему равна ширина спектра ЧМ сигнала?
4. Перечислите основные виды дискретной модуляции. Поясните принцип ОФМ.
5. Докажите, что при 
спектр сигнала при фазовой манипуляции ничем не отличается от спектра сигнала при балансной модуляции.
6. Назовите основные виды импульсной модуляций. Поясните их принцип.
7. Чем в основном определяется ширина спектра сигнала при импульсной модуляции?
8. Поясните принцип модуляции шумовой несущей.
9. Изобразите графически смещение спектра при шумовой и гармонической несущих.
10. Поясните принцип построения дискретных шумоподобных сигналов. Приведите примеры.
11. Является ли дискретная псевдослучайная последовательность случайным процессом? В чем ее сходство с шумом?
12. Как осуществляется модуляция шумоподобных сигналов?