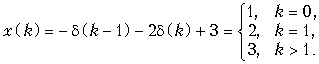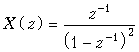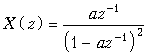При анализе и синтезе дискретных и цифровых цепей широко применяют так называемое z-преобразование. Это преобразование играет такую же основополагающую роль по отношению к дискретным сигналам, как преобразование Лапласа по отношению к аналоговым сигналам.

Z-преобразование дискретного сигнала. Заменим в уравнении (19.8) jw на комплексную переменную p:

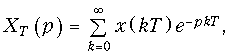(19.24)

таким образом, мы получим изображение по Лапласу дискретного сигнала. Оригинал, т. е. сам дискретный сигнал можно определить с помощью обратного преобразования Лапласа (7.4):

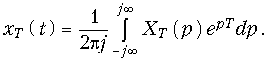(19.25)

Уравнение (19.25) определяет всю дискретную последовательность . Для определения одного, k-го отсчета формула (19.25) примет вид

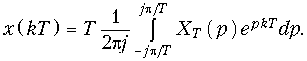(19.26)

Следует однако отметить, что X_T(p) является трансцендентной функцией переменной р вследствие наличия в (19.24) и (19.26) множителя e^±pkT.

Для перехода к рациональным функциям осуществим замену переменных:

(19.27)

Тогда формула (19.24) примет вид:

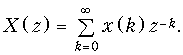(19.28)

Равенство (19.28) называют прямым односторонним z-преобразованием.

Обратное z-преобразование определяется формулой:

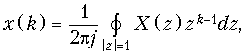(19.29)

где интегрирование осуществляется по окружности с радиусом |z| = 1.

Доказать справедливость (19.29) можно следующим образом. Пусть X(z) – функция комплексной переменной z, аналитическая в области |z| > r₀. Раскроем ряд (19.28):

(19.30)

Домножим левую и правую часть (19.30) на z^k–1:

(19.31)

Возьмем контурный интеграл от левой и правой части (19.31) вдоль кривой, лежащей целиком в области аналитичности и охватывающей все полюсы X(z) и учтем равенство Коши:

Тогда все слагаемые, кроме k-го обратятся в нуль:

Отсюда непосредственно следует (19.29), что и требовалось доказать.

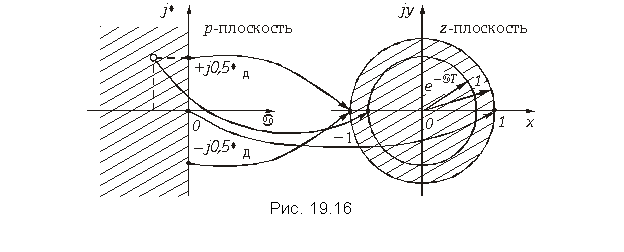
Установим связь между точками на комплексной плоскости p = = a + jw и z-плоскости z = x + jy (рис. 19.16).

Если положить a = 0, то мы будем перемещаться по оси jw в плоскости р. При переходе в z-плоскость точки мнимой оси jw будут располагаться на единичной окружности z = e^jwT. Причем, точка j0 на р-плоскости переходит в точку z = +1 на вещественной оси z-плоскости, а точки – в точку z = –1. Это означает, что точки отрезка () р-плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция e^±jwT периодическая, то последующие отрезки оси jw на p-плоскости такой же длины будут вновь проектироваться на единичную окружность.

Точкам левой р-полуплоскости соответствуют точки внутри единичной окружности z-плоскости, а точкам правой p-полуплоскости – точки вне этой окружности.

Пример. Рассчитаем z-преобразование дискретного сигнала x(k), имеющего вид

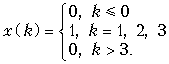
Воспользовавшись формулой (19.28), получим

.

Пример. Найдем z-преобразование X(z) дискретного экспоненциального сигнала x(k) = e^–akT.

Подставим значение x(k) в формулу (19.28), получим

.

Из теории рядов следует, что при выполнении условия |e^–aT×z^–1| < 1 сумма ряда X(z) равна 1/(1 – e^–aT×z^–1) или

.

Z-преобразование X(z) дискретного сигнала x(n) определено только для области z, в которой степенной ряд (19.28) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого называется радиусом сходимости (рис. 19.17), т. е. при r₀ < |z| < ¥ ряд сходится. В области сходимости существует взаимно однозначное соответствие между X(z) и x(k), т. е. каждому x(k) соответствует одно и только одно X(z), определенное для |z| > r₀ и наоборот.

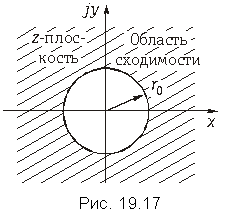
Пример. Определим радиус сходимости для z-преобразования сигнала, заданного в предыдущем примере.

Как уже было установлено, z-преобразование сигнала x(k) = e^–akT имеет вид

.

Нуль функции X(z) будет в точке z₀ = 0, полюс – в точке z_k = e^–aT. Следовательно, радиус сходимости r₀ = e^–aT, а функция X(z) сходится при |z| > e^–aT.

Окружность, имеющая радиус сходимости r₀ = e^–aT, приведена на рис. 19.16. Область сходимости находится за пределами этой окружности.

Пример. Найдем z-преобразование сигнала x(k) = Aa^k, k 0. Этот дискретный сигнал показан на рис. 19.18 для трех различных значений a: а = 0,8; а = 1; а = –0,8.

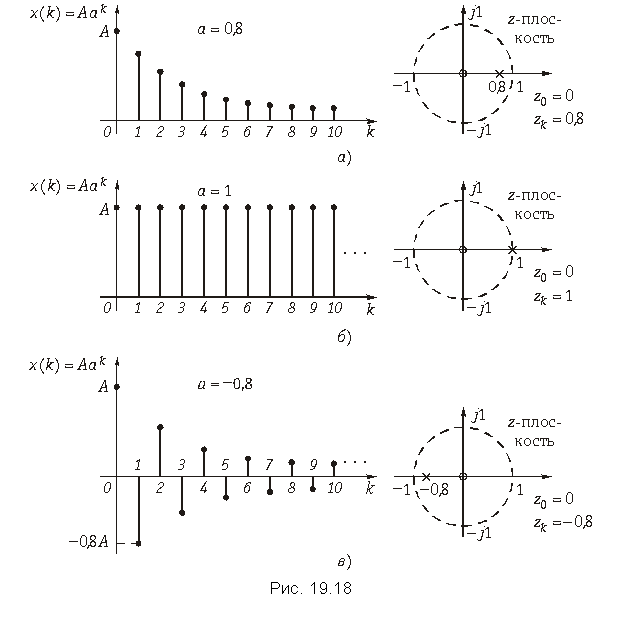
В соответствии с (19.28) z-преобразование такого дискретного сигнала равно

. (19.32)

Из математики известно, что этот ряд сходится к функции

, (19.33)

если |az^–1| < 1 или |z| > a.

Функция X(z) имеет нуль при z = 0, а ее полюс z_n = a лежит на окружности радиусом R₀ = a, ограничивающей область сходимости.

На рис. 19.18 показано расположение нуля и полюса функции X(z) в z-плоскости при различных а.

Нахождение дискретного сигнала по его z-изображению. Для этого можно воспользоваться обратным z-преобразованием (19.29).

Другой способ заключается в том, чтобы разложить функцию X(z) в степенной ряд по степеням z^–1. Тогда коэффициенты при степенях z^–1 будут, в соответствии с формулой (19.28), отсчетами дискретного сигнала x(k).

Пример. Найдем дискретный сигнал x(k), которому соответствует z-преобразование X(z) = 1/(1 – 0,5z^–1).

Воспользуемся разложением функции (1 – q)^–1 в ряд: 1 + q + q² + q³ + ....

Для заданного z-преобразования q = 0,5z^–1, поэтому запишем z-преобразование в виде

.

Сравнивая полученное выражение с общей формулой z-преобразования

, получим последовательность

x{k} = {1; 0,5; 0,25; 0,125; ...}.

Общий член этой последовательности x(k) = 0,5^k, k 0.

Пример. Найдем отсчеты дискретного сигнала по его z-преобразованию

.

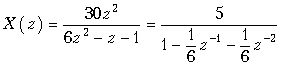Для разложения функции X(z) в степенной ряд по степеням z^–1 выполним деление числа 5 на многочлен . В результате получим частное . Отсчеты дискретного сигнала равны

и т. д.

Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе X(z), не слишком сложные.

Более эффективным способом нахождения x(k) по известному X(z) является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.

Пример. Найдем общий член x_k дискретного сигнала x(k), которому соответствует z-изображение, заданное в предыдущем примере

.

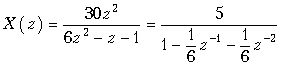Функция X(z) имеет полюсы в точках z₁ = 1/2 и z₂ = –1/3, или, что то же, в точках z₁^–1 = 2 и z₂^–1 = –3.

Разложим X(z) на сумму простых дробей:

.

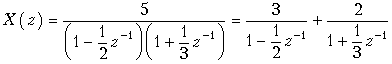Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления z(p) реактивных двухполюсников при синтезе их по схеме Фостера:

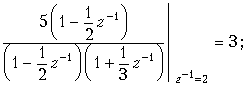
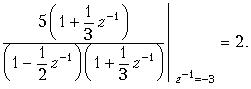
Подобно тому, как формула (19.33) представляет сумму ряда (19.32), простые дроби в (19.16) являются суммами рядов

и .

Поскольку z-преобразование – это линейная операция, то последовательность x(k) состоит из суммы двух последовательностей:

.

После выполнения операции возведения в степень k получим отсчеты дискретного сигнала

и т. д.

Свойства z-преобразования. Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z-преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.

Теорема линейности (суперпозиции). Сумме дискретных сигналов соответствует сумма их z-изображений. Если дискретным сигналам x(k) и y(k) соответствуют z-изображения X(z) и Y(z), то

,

где a и b – некоторые числа.

Доказательство теоремы выполните самостоятельно, используя выражение (19.28) для расчета z-изображения дискретного сигнала.

Теорема опережающего сдвига. Если дискретному сигналу x(k) соответствует одностороннее z-преобразование X(z), то сигналу, сдвинутому на один интервал дискретизации, x(k + 1) соответствует z-преобразование z(X(z) – x(0)).
Математическая запись теоремы имеет вид

,

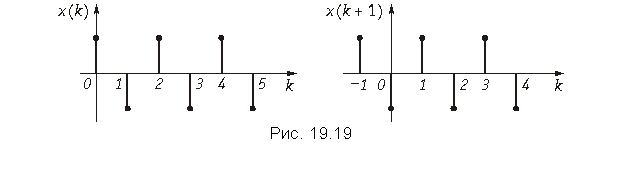
Чтобы доказать теорему, воспользуемся основным выражением (19.28) для расчета z-преобразования дискретных сигналов x(k) и x(k + 1), а также графиками, приведенными на рис. 19.19.

;

.

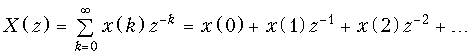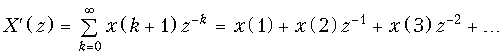Сравнивая X(z) и X¢(z), получаем X¢(z) = z(X(z) –x(0)), что и требовалось доказать.

Очевидно, что теорема опережающего сдвига выполняет ту же самую роль, что и теорема дифференцирования для преобразований Лапласа.

Теорема задержки. Математическая запись теоремы имеет вид

.

В теореме задержки u(k) – это дискретные отсчеты функции единичного скачка (рис. 19.20)

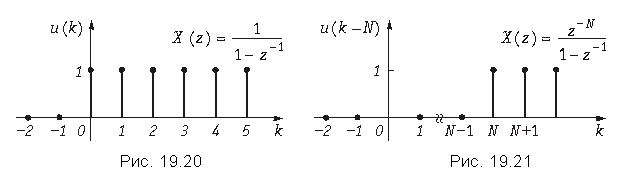
а u(k – N) – это дискретные отсчет функции u(k), задержанной на N интервалов дискретизации (рис. 19.25).

Доказательство вытекает из основного выражения (19.28) для z-преобразования.

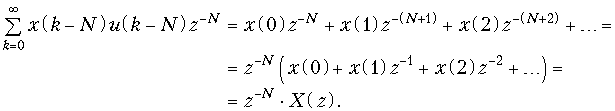
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т. е. при n < N. Из теоремы задержки в частности следует, что сдвиг дискретного сигнала на один интервал дискретизации T соответствует умножению z-преобразования на оператор z^–1, поэтому часто z^–1 называют оператором единичной задержки в z-области.

Теорема умножения на a^k. Математическая запись теоремы имеет вид

.

Теорема умножения на n.

.

Теоремы умножения дискретного сигнала x(k) на a^k и на k можно также доказать, используя формулу (19.28). Предлагаем проделать это самостоятельно.

Теорема свертки. Свертке дискретных сигналов x(k) и h(k) соответствует произведение их z-преобразований

.

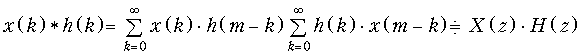Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в специальной литературе.

Пример. Найдем z-преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.

Найдем z-преобразование дискретного d-импульса d(k) (рис. 19.4), используя выражение (19.28)

.

Используя теорему задержки, найдем z-изображение сигнала d(k – N)

.

На рисунке 19.4 приведен также график задержанной функции единичного отсчета для частного случая N = 2.

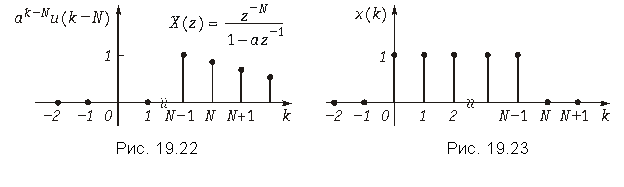
Пример. Найдем z-преобразование функции

.

В одном из примеров мы уже находили, что z-преобразование сигнала a^k имеет вид (19.33) X(z) = 1/(1 – az^–1).

Используя теорему задержки, получаем

.

При a = 1 имеем:

.

Графики дискретных сигналов u(k – N) и a^k–Nu(k – N) приведены на рис. 19.21 и 19.22.

Пример. Найдем z-преобразование дискретной последовательности x(k) = = ka^k, k 0.

Поскольку z-изображение последовательности a^k известно (19.15), то, используя теорему умножения на k, получим

.

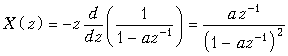Пример. Найдем z-преобразование дискретной последовательности из N отсчетов единичной амплитуды (рис. 19.23)

Сигнал x(k) можно представить как разность двух сигналов

.

Из теорем линейности и задержки легко получить z-преобразование

,

что совпадает с формулой для частичной суммы геометрической прогрессии

.

Табл. 19.1 – Краткая таблица односторонних z-преобразований

Пример. Вычислим z-преобразование свертки дискретных сигналов x{k} = = {1; 1; 1; 0; 0; 0; ...} и y{k} = {0; 0; 1; 1; 0; 0; ...}.

Найдем z-преобразование сигнала x(k), используя формулу (19.28)

.

Найдем z-преобразование сигнала y(k)

.

Вычислим z-преобразование свертки сигналов x(k) и y(k), используя теорему свертки

В табл. 19.1 дана сводка z-преобразований наиболее часто встречающихся дискретных последовательностей. Эти табличные сведения также могут быть использованы для расчета z-преобразований сигналов и перехода от z-преобразований к дискретным сигналам.

Пример. Найдем общий член дискретного сигнала x(k), которому соответствует z-изображение

.

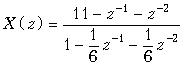Разложение функции X(z) на простые дроби приводит к выражению

.

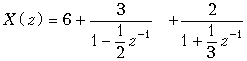Используя теорему линейности и находя в таблице 19.1 дискретные сигналы, соответствующие каждому из слагаемых в выражении X(z), получаем

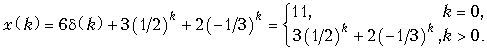
По этой формуле легко подсчитать значение x(k)для любого k. Аналогичным образом, разложение

приводит к последовательности