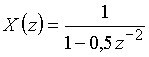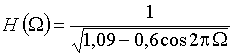Вопрос 1. Что такое дискретный сигнал?
Вопрос 2. Как часто следует брать отсчеты непрерывного сигнала?
Вопрос 3. Зачем переходить от непрерывного сигнала к дискретному?
Вопрос 4. В чем различие спектров непрерывного и дискретного сигналов?
Вопрос 5. Почему происходят наложения сигналов и спектров?
Вопрос 6. Как восстанавливают непрерывный сигнал из дискретного?
Вопрос 7. О чем гласит теорема В.А. Котельникова?
Вопрос 8. Зачем используют дискретное преобразование Фурье?
Вопрос 9. Что такое z-преобразование дискретного сигнала?
Вопрос 10. Как найти дискретный сигнал по его z-преобразованию?
Вопрос 11. Какими свойствами обладает z-преобразование?
Вопрос 12. Что такое дискретные цепи и чем они отличаются от аналоговых цепей?
Вопрос 13. Что такое цифровые цепи и чем они отличаются от дискретных цепей?
Вопрос 14. Как определять передаточную функцию дискретной цепи?
Вопрос 15. Что такое нерекурсивные и рекурсивные дискретные цепи?
Вопрос 16. Где располагаются полюсы передаточной функции устойчивой дискретной цепи?
Вопрос 17. Как построить амплитудно-частотную характеристику дискретной цепи?
Вопрос 18. Существуют ли типовые звенья дискретных цепей?
Вопрос 19. Как соединяются между собой типовые звенья?
Вопрос 20. Может ли дискретная цепь осуществлять фильтрацию сигнала?
Вопрос 22. Как рассчитать аналоговый фильтр-прототип?
Вопрос 23. Как осуществить переход к дискретному фильтру?
Вопрос 24. Как реализовать фильтр с конечной импульсной характеристикой?
Вопрос 25. Как рассчитываются дискретные фильтры верхних частот, полосовые и режекторные?
Вопрос 26. В чем состоят особенности расчета цифровых фильтров?
Введение
Этот материал является базовым для понимания процессов цифровой фильтрации и обработки сигналов во многих современных информационных системах.
По своей природе многие сигналы являются непрерывными. Это объясняется тем, что источники сообщений выдают информацию непрерывно, в любые моменты времени. К таким источникам относятся, например, микрофоны телефонных аппаратов, считывающие устройства факсимильных аппаратов, передающие телевизионные камеры.
Дискретные сигналы естественно возникают в тех случаях, когда источник сообщений выдает информацию в фиксированные моменты времени. Например, устройство измерения температуры, связанное с городским световым табло, посылает сигнал на это табло в определенные промежутки времени. В других промежутках на табло высвечиваются давление, время или другие параметры. Здесь ярко проявляется характер дискретного сигнала: в паузах нет никаких сведений об изменении температуры. Таким образом, мы имеем дело не с непрерывным изменением температуры, а лишь с ее значениями, отсчитанными через определенные промежутки времени. Подобный процесс называется дискретизацией непрерывного сигнала.
Свойство дискретного сигнала - существовать лишь в определенные промежутки времени - позволяет организовать передачу по одной и той же линии (радиоканалу, паре проводов, оптическому волокну) сообщений от нескольких различных источников. Примером этого служит упомянутая выше передача на городское световое табло сведений от датчиков температуры, давления и т.п. Говорят, что при этом происходит разделение каналов во времени.
Особой разновидностью дискретных сигналов являются цифровые сигналы. Цифровой сигнал - это последовательность импульсов. Если принять условно факт наличия импульса за 1, а факт его отсутствия за 0, то импульсную последовательность можно представить как чередование двух цифр: 0 и 1.
Число, которое принимает только значение 0 и 1 называется «двоичной цифрой». Отсюда и появилось название «цифровой сигнал».
Очевидно, что любое значение дискретного сигнала легко перевести в двоичное число. Поэтому цифровой сигнал можно рассматривать как закодированный двоичным кодом дискретный сигнал.
В последнее время системы с цифровыми сигналами активно вторгаются в нашу жизнь. Во всем мире сейчас пользуются цифровыми телефонами; в наши дома приходит цифровое телевидение; на прилавках магазинов мы видим аппаратуру цифровой звуко- и видеозаписи.
Цифровые сигналы в телефонии, телевидении, звуко- и видеозаписи ничем не отличаются от цифровых сигналов в компьютерных сетях. Появляется возможность применять для обработки текста, звука, изображения быстродействующие компьютерные системы. Для передачи телекоммуникационных сигналов теперь могут использоваться компьютерные сети, а для передачи компьютерных сигналов - обычная телефонная сеть.
Вопрос 1. Что такое дискретный сигнал?
Сигнал – это физический процесс (например, изменяющиеся во времени токи и напряжения), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.
Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией ![]() , которая может принимать любые значения в определенном интервале; дискретные сигналы
, которая может принимать любые значения в определенном интервале; дискретные сигналы ![]() представляют собой последовательности или отсчеты функции
представляют собой последовательности или отсчеты функции ![]() , взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.
, взятые в определенные дискретные моменты времени nT; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.
Если в цепь микрофона (рис. 1), где ток ![]() является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
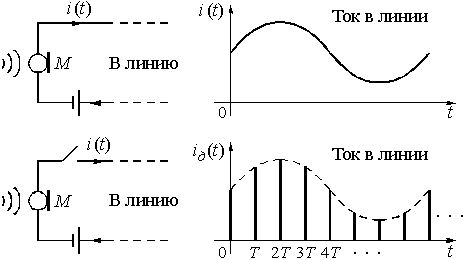
Рис. 1
В отличие от непрерывного сигнала ![]() дискретный сигнал можно обозначить
дискретный сигнал можно обозначить ![]() . Однако, чаще его обозначают
. Однако, чаще его обозначают ![]() , заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения:
, заменяя непрерывное время t дискретными моментами nT, следующими строго через интервал T. Используются и более краткие обозначения: ![]() и
и ![]() . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал
. Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n < 0 дискретный сигнал ![]() . При n = 0 значение
. При n = 0 значение ![]() равно значению сигнала
равно значению сигнала ![]() в момент времени t = 0. При n > 0 отсчеты
в момент времени t = 0. При n > 0 отсчеты ![]() повторяют форму сигнала
повторяют форму сигнала ![]() , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.
, т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT.
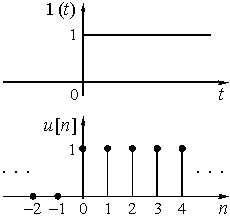
Рис. 2
Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, ![]() , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
, в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов.
Пример 1.1. Единичный ступенчатый аналоговый сигнал ![]() приведен на рис. 2.
приведен на рис. 2.
Соответствующий ему дискретный сигнал ![]() называется ступенчатой последовательностью. Он определяется следующим образом:
называется ступенчатой последовательностью. Он определяется следующим образом:

Рис. 3
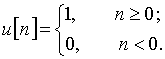
Такая последовательность приведена на рис. 2.
Пример 1.2. Импульс Дирака или d-функция в аналоговой области приведена на рис. 3.

Рис. 4
Дельта-последовательность или дискретная d-функция определяется выражением
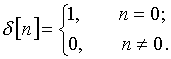
Последовательность ![]() , приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:
, приведенная на рис. 3, принимает единственное значение, равное 1, при n = 0. Этот сигнал можно сдвинуть на k интервалов:
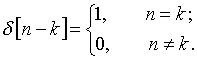
Тогда математическая запись любого дискретного сигнала имеет вид
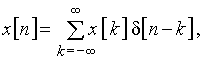
где ![]() – отсчеты исходного аналогового сигнала.
– отсчеты исходного аналогового сигнала.
Этот сигнал можно получить из аналогового (рис. 4) периодическим замыканием ключа на очень короткое время в моменты t = k.
Самоконтроль
1. Что представляют собой аналоговые, дискретные и цифровые сигналы?
2. Как практически получить дискретный сигнал из аналогового?
3. Что такое ступенчатая последовательность и дельта-последовательность?
4. Изобразите графики дискретных d-функций ![]() и
и ![]() .
.
Вопрос 2. Как часто следует брать отсчеты непрерывного сигнала?
Интервал времени T, через который отсчитываются значения непрерывного сигнала ![]() , называется интервалом дискретизации. Обратная величина 1/T (обозначим ее
, называется интервалом дискретизации. Обратная величина 1/T (обозначим ее ![]() ) называется частотой взятия отсчетов или частотой дискретизации.
) называется частотой взятия отсчетов или частотой дискретизации.
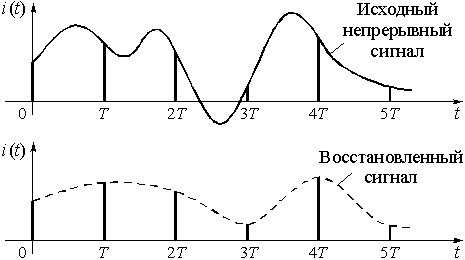
Рис. 5
Отсчеты непрерывного сигнала следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет потеряна и форма восстановленного сигнала будет отличаться от формы исходного (рис. 5). Если обратиться к схеме рис. 1, то это означает, что звук на приеме будет восприниматься с искажениями.
Для сигналов с ограниченным спектром, т.е. для тех сигналов, у которых спектральная плотность локализована в определенной полосе частот, существуют более конкретные рекомендации по выбору интервала дискретизации Т (или, что то же, частоты дискретизации ![]() ). Эти рекомендации будут даны позже.
). Эти рекомендации будут даны позже.
Самоконтроль
1. Что такое интервал дискретизации и частота дискретизации?
2. Почему нельзя произвольно выбирать интервал дискретизации?
3. Уменьшите в два раза интервал дискретизации T исходного аналогового сигнала (рис. 5) и, восстановив сигнал по его дискретным отсчетам, сравните с тем, что приведен на рисунке.
Вопрос 3. Зачем переходить от непрерывного сигнала к дискретному?
Получение, передача и обработка непрерывных сигналов (например, речевые сигналы в телефонии и радиовещании, телевизионные сигналы) может осуществляться в аналоговой форме.
На рис. 6 показана RC-цепь, у которой импульсная характеристика, как известно, равна
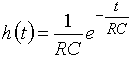 .
.
Если задано напряжение на входе цепи ![]() и нужно найти напряжение на ее выходе
и нужно найти напряжение на ее выходе ![]() , мы можем сделать это, воспользовавшись интегралом свертки:
, мы можем сделать это, воспользовавшись интегралом свертки:
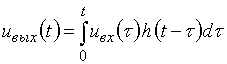 . (1)
. (1)
Это известный материал и мы лишь напомним его.
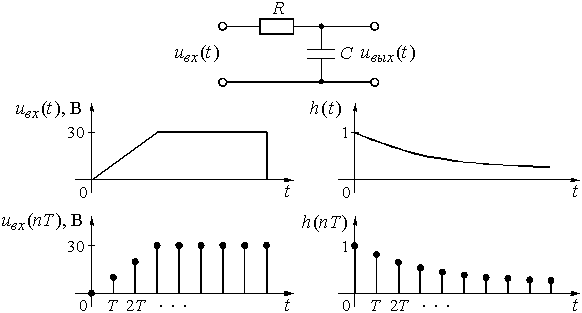
Рис. 6
При передаче аналоговых сигналов необходимо учитывать влияние помех и нестабильность параметров цепи, т.е. их зависимость от времени, температуры, влажности и т.д. Особенно сильно это влияние сказывается на очень низких частотах (меньше 1 Гц) и на частотах выше 20 кГц. В диапазоне сигналов звуковых частот характеристики аналоговых и дискретных цепей и сигналов сопоставимы, и выбор типа сигнала определяется прогрессом в технологии изготовления и применения современных средств микроэлектроники, а они, в свою очередь, ориентированы на цифровые устройства.
Заменим непрерывные сигналы в схеме рис. 6 и формуле (1) их дискретными отсчетами. Чтобы не вносить путаницы, время t заменим дискретными значениями nT, а время t – дискретными значениями mT. Тогда интеграл придется заменить суммой и выражение (1) запишется в виде:
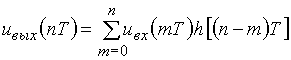 . (2)
. (2)
Вместо непрерывного сигнала ![]() мы будем иметь дело с дискретным сигналом
мы будем иметь дело с дискретным сигналом ![]() и вместо непрерывной импульсной характеристики
и вместо непрерывной импульсной характеристики ![]() – с дискретной импульсной характеристикой
– с дискретной импульсной характеристикой
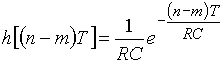 .
.
Поскольку любой отсчет сигнала – это число, то формулу (2) можно запрограммировать на ЭВМ. Останется лишь ввести в ЭВМ числа, соответствующие всем дискретным отсчетам ![]() и
и ![]() , и она вычислит отсчеты выходного напряжения
, и она вычислит отсчеты выходного напряжения ![]() . Выражение (2) на языке вычислительной техники называется алгоритмом вычисления выходного сигнала.
. Выражение (2) на языке вычислительной техники называется алгоритмом вычисления выходного сигнала.
Пример 1.3. Рассчитаем отсчеты выходного напряжения![]() в цепи, приведенной на рис. 6.
в цепи, приведенной на рис. 6.
Для расчета воспользуемся формулой (2), подставляя в нее соответствующие дискретные отсчеты входного сигнала ![]() и дискретные отсчеты импульсной характеристики
и дискретные отсчеты импульсной характеристики ![]() , графики которых приведены на рис. 6.
, графики которых приведены на рис. 6.
![]() ;
;
![]() ;
;
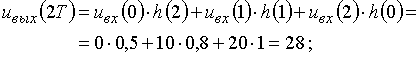
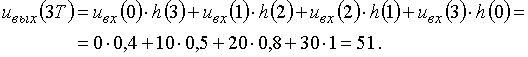
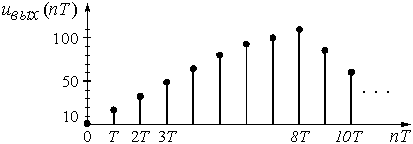
Рис. 7
Аналогичным образом рассчитываются ![]() = 68;
= 68; ![]() = 80,5;
= 80,5; ![]() = 91;
= 91; ![]() = 100,3;
= 100,3; ![]() = 108,6;
= 108,6; ![]() = 83,4;
= 83,4; ![]() = 59 и т.д.
= 59 и т.д.
График последовательности ![]() приведен на рис. 7.
приведен на рис. 7.
Таким образом, дискретные сигналы удобны тем, что их можно обрабатывать с помощью ЭВМ. Однако, не следует думать, что дискретные сигналы вносятся в ЭВМ лишь с клавиатуры. Их можно вводить в ЭВМ и выводить из нее непосредственно.
На рис. 8 показано, как это делать. Непрерывный сигнал ![]() подается на ключ, на выходе которого образуются дискретные отсчеты
подается на ключ, на выходе которого образуются дискретные отсчеты ![]() . Но их еще нельзя ввести в машину. Сначала нужно перевести амплитуды отсчетов в двоичный код – ведь только такой код понимает ЭВМ. Выполняет эту операцию кодер. Скажем, если отсчет имеет величину 30 В, то запись числа 30 в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на рисунке обозначены
. Но их еще нельзя ввести в машину. Сначала нужно перевести амплитуды отсчетов в двоичный код – ведь только такой код понимает ЭВМ. Выполняет эту операцию кодер. Скажем, если отсчет имеет величину 30 В, то запись числа 30 в двоичном 8-разрядном коде будет такой: 00011110. Закодированные в двоичном коде отсчеты на рисунке обозначены ![]() .
.
Вычислительные средства (ВС) могут представлять собой универсальную большую ЭВМ, специализированную микро-ЭВМ, микропроцессорное устройство или что-нибудь в этом роде. Главное состоит в том, что в памяти ЭВМ записана программа вычисления, например, выражение (2), и отсчеты импульсной реакции, скажем, RC-цепи. Следовательно, в результате работы программы, ЭВМ будет выдавать закодированные в двоичном коде отсчеты ![]() . Декодер преобразует код в амплитуду, и на его выходе появляются дискретные отсчеты выходного напряжения
. Декодер преобразует код в амплитуду, и на его выходе появляются дискретные отсчеты выходного напряжения ![]() . Интерполятор (Инт) восстанавливает функцию между отсчетами. В итоге на выходе системы мы имеем аналоговый сигнал
. Интерполятор (Инт) восстанавливает функцию между отсчетами. В итоге на выходе системы мы имеем аналоговый сигнал ![]() .
.
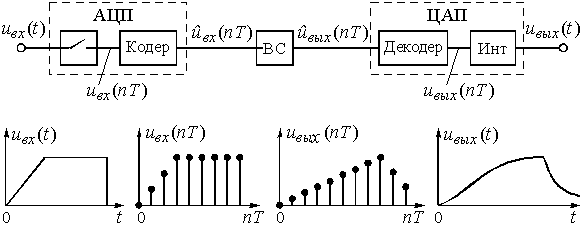
Рис. 8
Устройство, состоящее из ключа и кодера и преобразующее непрерывный (аналоговый) сигнал в двоичный код (или, что то же,в цифровой сигнал), называют аналого-цифровым преобразователем (АЦП). Обратное преобразование выполняет цифро-аналоговый преобразователь (ЦАП), содержащий декодер и интерполятор.
Как видим, ЭВМ может сыграть роль реальной цепи. И хотя самой физической цепи может и не быть в наличии, а задана она будет лишь в виде отсчетов импульсной реакции и программы вычислений, мы будем наблюдать на выходе описанной системы такое же выходное напряжение ![]() , как и на выходе реальной цепи.
, как и на выходе реальной цепи.
Самоконтроль
1. Почему удобно передавать и обрабатывать дискретные сигналы?
2. Рассчитайте первые два отсчета напряжения на выходе дискретной цепи, имеющей импульсную характеристику
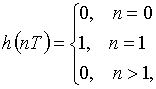
если напряжение на ее входе 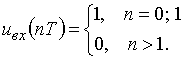
3. Поясните по графикам, как работает цепь, изображенная на рис. 8.
Вопрос 4. В чем различие спектров непрерывного и дискретного сигналов?
Комплексная спектральная плотность ![]() непрерывного сигнала
непрерывного сигнала ![]() (в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье
(в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье
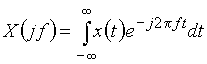 . (3)
. (3)
Сигнал ![]() может быть восстановлен по спектру
может быть восстановлен по спектру ![]() с помощью обратного преобразования Фурье, или интеграла Фурье
с помощью обратного преобразования Фурье, или интеграла Фурье
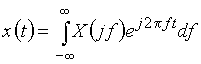 . (4)
. (4)
В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром (рис. 9, а). И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени (рис. 10, а). Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр.
Если сигнал ![]() является периодическим, то спектр его – дискретный, т.е. теперь вместо
является периодическим, то спектр его – дискретный, т.е. теперь вместо ![]() используют отсчеты
используют отсчеты ![]() . Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала
. Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала ![]() . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае
. Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае ![]() . Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник
. Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник ![]() периодического сигнала и отсчетами
периодического сигнала и отсчетами ![]() спектральной плотности
спектральной плотности ![]() непрерывного сигнала:
непрерывного сигнала:
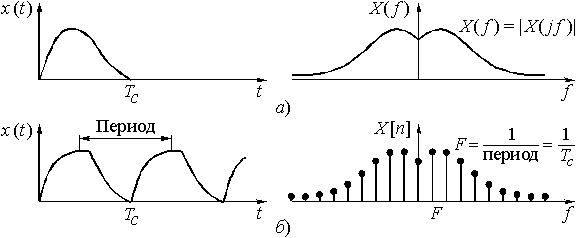
Рис. 9
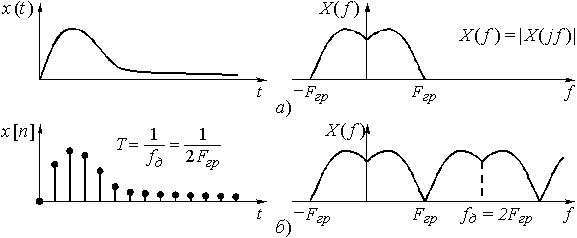
Рис. 10
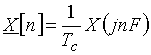 .
.
Спектр ![]() периодического сигнала вычисляется по формуле
периодического сигнала вычисляется по формуле
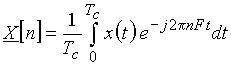 . (5)
. (5)
Сигнал ![]() можно восстановить по его дискретному спектру, воспользовавшись формулой
можно восстановить по его дискретному спектру, воспользовавшись формулой
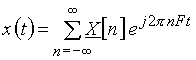 . (6)
. (6)
В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рис. 10, б). Обозначая период повторения спектра ![]() , получим интервал дискретизации сигнала
, получим интервал дискретизации сигнала ![]() .
.
Формулы прямого и обратного преобразований Фурье для дискретных сигналов имеют вид
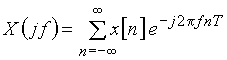 ; (7)
; (7)
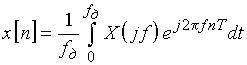 . (8)
. (8)
В формулах (7) и (8) использовано обозначение ![]() .
.
Пример 4.1. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета ![]() .
.
Воспользуемся формулой (7), в которую подставим значения ![]() заданного сигнала
заданного сигнала
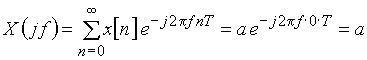 .
.
Пример 4.2. Рассчитаем спектр экспоненциальной дискретной функции ![]() , n³ 0.
, n³ 0.
График дискретной функции ![]() приведен на рис. 11, а ее отсчеты можно записать в виде последовательности
приведен на рис. 11, а ее отсчеты можно записать в виде последовательности ![]() {1; 0,5; 0,25; 0,125; 0,0625; ...}.
{1; 0,5; 0,25; 0,125; 0,0625; ...}.
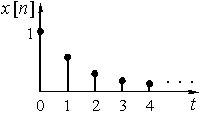
Рис. 11
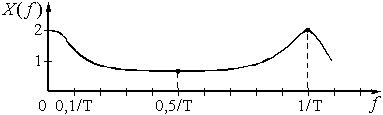
Рис. 12
Спектр дискретной экспоненты рассчитаем по формуле (7)
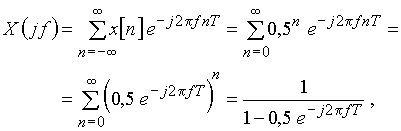
где для суммирования ряда использована формула
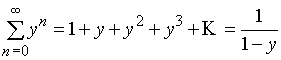 .
.
Получим выражение для расчета спектра амплитуд ![]() , используя формулу Эйлера
, используя формулу Эйлера ![]() .
.
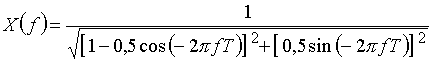 .
.
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать ![]() .
.
График спектра амплитуд ![]() экспоненциальной дискретной функции
экспоненциальной дискретной функции ![]() приведен на рисунке 12.
приведен на рисунке 12.
Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом ![]() .
.
Самоконтроль
1. Как рассчитывается спектр непериодического (и периодического) непрерывного сигнала?
2. Как восстановить непрерывный сигнал по его спектру (сплошному и дискретному)?
3. Сформулируйте принцип неопределенности.
4. Как рассчитывается спектр дискретного сигнала?
5. Какой спектр у дискретного сигнала: сплошной или дискретный, периодический или непериодический?
6. Как рассчитывается дискретный сигнал, если известен его спектр?
7. Найдите спектр дискретного сигнала, состоящего из одного отсчета ![]() .
.
8. Найдите значения спектра дискретного сигнала, заданного двумя отсчетами ![]() , на частотах
, на частотах ![]() и
и ![]() .
.
Вопрос 5. Почему происходят наложения сигналов и спектров?
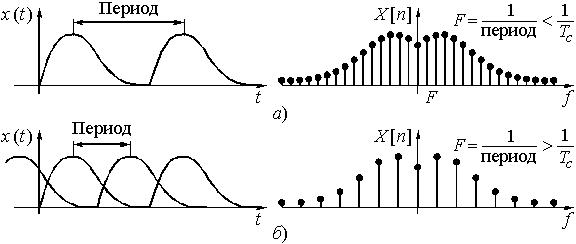
Рис. 13
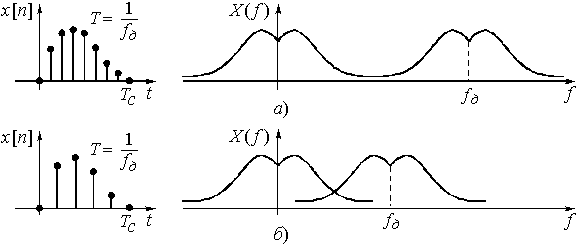
Рис. 14
Обратимся вновь к рис. 9. В случае, когда дискретизации подвергается спектр (рис. 9, б), это приводит к периодическому повторению сигнала. На рис. 9, б и 13, а, б показаны случаи выбора разных интервалов дискретизации спектров. При слишком редкой дискретизации и происходит наложение сигналов из разных периодов друг на друга (рис. 13, б). При этом форма периодической последовательности будет отличаться от формы одиночного сигнала.
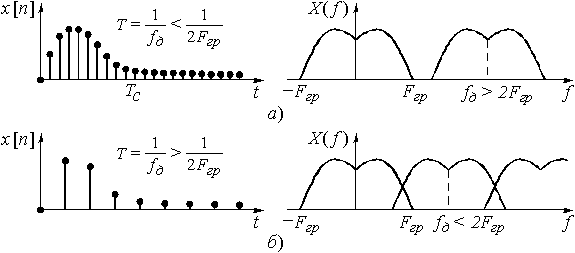
Рис. 15
Если дискретизации подвергается сигнал (рис. 14, а, б и 15 а, б), то периодически повторяется спектр сигнала. При неудачном выборе интервала дискретизации будет иметь место наложение друг на друга спектров из разных периодов повторения, т.е. искажение формы спектра (рис. 14, б и 15, б).
Вывод: все наложения (сигналов или спектров) происходят из-за неудачного – слишком редкого – интервала дискретизации (соответственно, спектра или сигнала). Это приводит к появлению ошибок наложения, или, другими словами, искажений формы сигнала (либо спектра) на каждом периоде.
Самоконтроль
1. Почему нельзя выбирать большой интервал дискретизации сигнала (или спектра)?
2. Каким должно быть соотношение между интервалом дискретизации спектра по частоте F и периодом повторения ![]() сигнала, чтобы не было наложения сигналов?
сигнала, чтобы не было наложения сигналов?
3. Постройте спектр ![]() сигнала, приведенного на рис. 15, если
сигнала, приведенного на рис. 15, если ![]() . Будет ли в этом случае наложение спектров?
. Будет ли в этом случае наложение спектров?
Вопрос 6. Как восстанавливают непрерывный сигнал из дискретного?
На рис. 8 устройство, восстанавливающее непрерывный сигнал из дискретного, было названо интерполятором. Оно по известным (отсчетным) значениям непрерывной функции вычисляет все промежуточные значения. В математике подобная операция называется интерполяцией.
Можно взглянуть на эту проблему и с другой стороны. Спектр дискретного сигнала содержит (в самом первом периоде) спектр исходного, недискретизированного сигнала (рис. 10, б, 14, а и 15, а). Пропустим дискретный сигнал ![]() через фильтр нижних частот с граничной частотой полосы пропускания
через фильтр нижних частот с граничной частотой полосы пропускания ![]() . Такой фильтр подавит все «боковые» спектры и не внесет никаких изменений в «основной» спектр. Значит, на его выходе появится непрерывный сигнал
. Такой фильтр подавит все «боковые» спектры и не внесет никаких изменений в «основной» спектр. Значит, на его выходе появится непрерывный сигнал ![]() . Таким образом, фильтр нижних частот с частотой среза
. Таким образом, фильтр нижних частот с частотой среза ![]() может играть роль интерполятора.
может играть роль интерполятора.
Самоконтроль
1. Каким образом фильтр нижних частот выполняет операцию интерполяции?
2. Можно ли точно восстановить непрерывные сигналы из дискретных сигналов ![]() , приведенных на рис. 14, а и 15, б?
, приведенных на рис. 14, а и 15, б?
Вопрос 7. О чем гласит теорема В.А. Котельникова?
В 1933 году в работе «О пропускной способности «эфира» и проволоки в электросвязи» В.А. Котельников доказал теорему, ставшую основополагающей в теории и технике цифровой связи. Она гласит: если непрерывный сигнал ![]() имеет спектр, ограниченный частотой
имеет спектр, ограниченный частотой ![]() , то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени
, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени ![]() , т.е. с частотой
, т.е. с частотой ![]() .
.
Мы не приводим полную математическую формулировку теоремы, а также ее доказательство, а лишь ограничиваемся указанием сути теоремы. Однако, справедливость ее легко усматривается из рис. 10, б и 15, а. Частота дискретизации непрерывного сигнала не должна быть меньше удвоенной ширины спектра: ![]() иначе произойдет наложение спектров (рис. 15, б) и будет невозможно с помощью фильтра нижних частот выделить спектр исходного непрерывного сигнала.
иначе произойдет наложение спектров (рис. 15, б) и будет невозможно с помощью фильтра нижних частот выделить спектр исходного непрерывного сигнала.
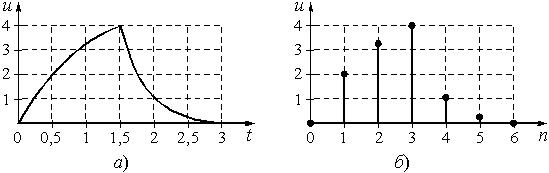
Рис. 16
Пример 7.1. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.
Из условия задачи следует, что граничная частота спектра ![]() равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
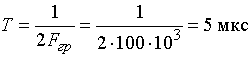 .
.
Минимально допустимая частота дискретизации ![]() = 2 ×× 100 = 200 кГц.
= 2 ×× 100 = 200 кГц.
Пример 7.2. Определим дискретные отсчеты сигнала длительностью ![]() = 3 мс, приведенного на рис. 16, а, если в качестве граничной частоты спектра
= 3 мс, приведенного на рис. 16, а, если в качестве граничной частоты спектра ![]() принять значение
принять значение ![]() , выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих ![]() , привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
Граничная частота спектра 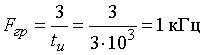 .
.
Интервал дискретизации 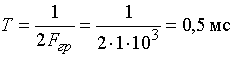 .
.
Берем отсчеты сигнала, приведенного на рис. 16, а, через интервал времени T = 0,5 мс и получаем последовательность![]() = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 16, б.
= {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 16, б.
Самоконтроль
1. Как нужно выбирать интервал дискретизации сигнала, чтобы можно было однозначно восстановить непрерывный сигнал по его дискретным отсчетам?
2. Как выбирается минимальная частота дискретизации?
3. Найдите частоту дискретизации и интервал дискретизации сигнала, имеющего спектр, ограниченный частотой ![]() = 10 кГц.
= 10 кГц.
4. Уменьшите в 2 раза интервал дискретизации по сравнению с тем значением, которое получили в п. 3. Можно ли при этом однозначно восстановить непрерывный сигнал? Как изменится спектр сигнала?
Вопрос 8. Зачем используют дискретное преобразование Фурье?
Мы уже отмечали, что развитие вычислительной техники привело к появлению цифровых систем обработки сигналов. При этом как сигнал, так и его спектр необходимо перед вводом в вычислительное устройство представлять в виде отсчетов, т.е. в виде чисел.
В формулах (5) и (6), или (7) и (8), один из компонентов уже является дискретным. Остается только заменить в этих формулах оставшуюся непрерывную переменную (t или f) дискретными значениями.
Так, например, если в формулах (5) и (6) время t заменим на nT, то получим формулы (9) и (10)
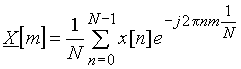 , (9)
, (9)
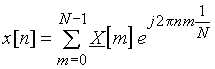 . (10)
. (10)
Следует заметить, что при этом периодический сигнал ![]() стал дискретным сигналом
стал дискретным сигналом ![]() , или
, или ![]() , а значит дискретный спектр
, а значит дискретный спектр ![]() начал периодически повторяться (рис. 17). Суммирование дискретных составляющих спектра
начал периодически повторяться (рис. 17). Суммирование дискретных составляющих спектра ![]() в формуле (6) следует теперь вести не в бесконечных пределах, а на периоде, где укладывается N отсчетов. Значит индекс суммирования m в формуле (10) будет изменяться от m = 0 до m = N – 1.
в формуле (6) следует теперь вести не в бесконечных пределах, а на периоде, где укладывается N отсчетов. Значит индекс суммирования m в формуле (10) будет изменяться от m = 0 до m = N – 1.
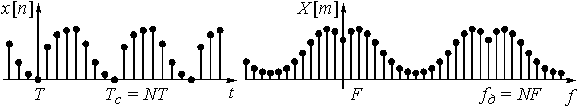
Рис.17
На периоде повторения ![]() дискретного сигнала
дискретного сигнала ![]() также укладывается N отсчетов, включая нулевой отсчет. Интеграл в (5) заменяется суммой с индексом суммирования n, изменяющимся от n = 0 до n = N – 1. Переменная dt в этой формуле при переходе от интеграла к сумме заменяется на T, так что отношение
также укладывается N отсчетов, включая нулевой отсчет. Интеграл в (5) заменяется суммой с индексом суммирования n, изменяющимся от n = 0 до n = N – 1. Переменная dt в этой формуле при переходе от интеграла к сумме заменяется на T, так что отношение ![]() , т.к.
, т.к. ![]() . Частота дискретизации равна
. Частота дискретизации равна ![]() . Отсюда вытекают соотношения:
. Отсюда вытекают соотношения:
![]() и
и ![]() . (11)
. (11)
Произведение FT можно заменить величиной 1/N.
Выражения (9) и (10) называются прямым и обратным дискретным преобразованием Фурье.
Вывод: Формулы дискретного преобразования Фурье (ДПФ) удобны для расчетов на ЭВМ.
Пример 8.1. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами ![]() = {0; 1; 2}.
= {0; 1; 2}.
Для расчета воспользуемся формулой ДПФ (9).
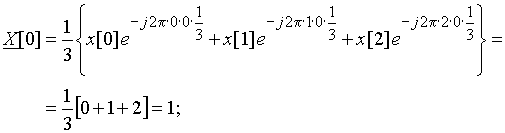
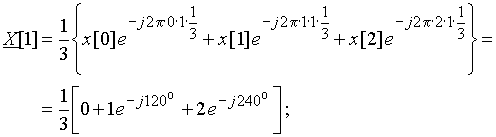
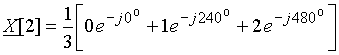 .
.
Поскольку
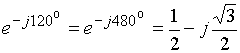 ,
, 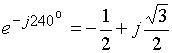 ,
,
то ![]() ,
,
![]() .
.
Графики заданного дискретного периодического сигнала ![]() и рассчитанного дискретного периодического спектра амплитуд
и рассчитанного дискретного периодического спектра амплитуд ![]() приведены на рис. 18.
приведены на рис. 18.
Пример 8.2. Рассчитаем значения дискретного сигнала ![]() , ДПФ которого имеет вид
, ДПФ которого имеет вид ![]() = {0; 1; 0; 1}.
= {0; 1; 0; 1}.
Значения дискретного сигнала ![]() будем рассчитывать по формуле (10)
будем рассчитывать по формуле (10)
![]() ;
;
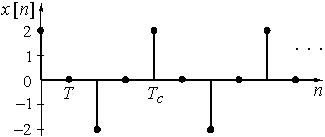
Рис. 19
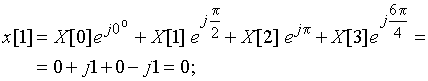
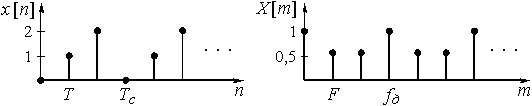
Рис. 18
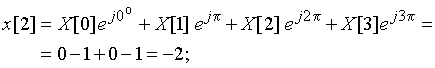
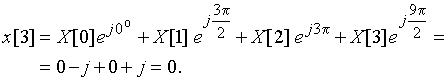
График последовательности ![]() = {2; 0; –2; 0} приведен на рис. 19. Сигнал
= {2; 0; –2; 0} приведен на рис. 19. Сигнал ![]() дискретный и периодический.
дискретный и периодический.
Самоконтроль
1. Как рассчитать спектр дискретного периодического сигнала?
2. Как рассчитать дискретный периодический сигнал по его спектру?
3. Найдите ДПФ сигнала, заданного двумя отсчетами ![]() = {1; –1}.
= {1; –1}.
4. Рассчитайте значения ![]() и
и ![]() дискретного сигнала, ДПФ которого имеет вид
дискретного сигнала, ДПФ которого имеет вид ![]() = {1; –1}.
= {1; –1}.
Вопрос 9. Что такое z-преобразование дискретного сигнала?
Дискретный сигнал и его спектр описываются формулами (8) и (7).
Произведем в формуле (7) замену:
![]() .
.
Тогда формула примет вид:
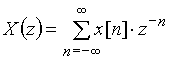 . (12)
. (12)
Выражение (12) получило название z-преобразования или z-изображения дискретного сигнала ![]() . Если начать суммирование с n = 0, то выражение
. Если начать суммирование с n = 0, то выражение
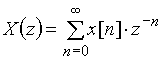 . (13)
. (13)
есть одностороннее z-преобразование. Оно применяется для сигналов ![]() º 0 при n < 0.
º 0 при n < 0.
Можно указать на связь z-преобразования с преобразование Лапласа дискретного сигнала
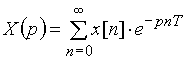 ,
,
которое легко получить из (7), положив ![]() .
.
Очевидно, что ![]() или
или ![]() .
.
Эти формулы устанавливают связь между точками в плоскостях ![]() и
и ![]() (рис. 20).
(рис. 20).
Если положить a = 0, то мы будем перемещаться по оси jw в плоскости р. При переходе в z-плоскость точки мнимой оси jw будут располагаться на единичной окружности ![]() . Причем, точка j0 на р-плоскости переходит в точку z = +1 на вещественной оси z-плоскости, а точки
. Причем, точка j0 на р-плоскости переходит в точку z = +1 на вещественной оси z-плоскости, а точки ![]() – в точку z = –1. Это означает, что точки отрезка (
– в точку z = –1. Это означает, что точки отрезка (![]() ) р-плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция
) р-плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция ![]() периодическая, то последующие отрезки оси jw на p-плоскости такой же длины будут вновь проектироваться на единичную окружность.
периодическая, то последующие отрезки оси jw на p-плоскости такой же длины будут вновь проектироваться на единичную окружность.
Точкам левой р-полуплоскости соответствуют точки внутри единичной окружности z-плоскости, а точкам правой p-полуплоскости – точки вне этой окружности.
Пример 9.1. Рассчитаем z-преобразование дискретного сигнала ![]() , имеющего вид
, имеющего вид
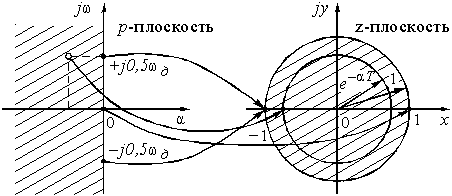
Рис. 20
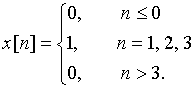
Воспользовавшись формулой (13), получим
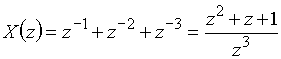 .
.
Пример 9.2. Найдем z-преобразование ![]() дискретного экспоненциального сигнала
дискретного экспоненциального сигнала![]() .
.
Подставим значение ![]() в формулу (13), получим
в формулу (13), получим
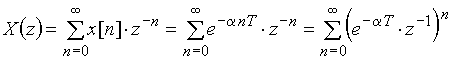 .
.
Из теории рядов следует, что при выполнении условия ![]() сумма ряда
сумма ряда ![]() равна
равна 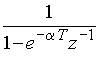 или
или 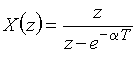 .
.
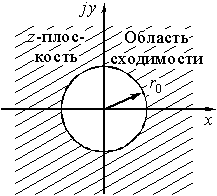
Рис. 21
Z-преобразование ![]() дискретного сигнала
дискретного сигнала ![]() определено только для области z, в которой степенной ряд (13) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого
определено только для области z, в которой степенной ряд (13) сходится. Эта область сходимости включает в себя все значения z, находящиеся вне некоторого круга на комплексной z-плоскости, радиус которого ![]() называется радиусом сходимости (рис. 21), т.е. при
называется радиусом сходимости (рис. 21), т.е. при ![]() ряд сходится. В области сходимости существует взаимно-однозначное соответствие между
ряд сходится. В области сходимости существует взаимно-однозначное соответствие между ![]() и
и ![]() , т.е. каждому
, т.е. каждому ![]() соответствует одно и только одно
соответствует одно и только одно ![]() , определенное для
, определенное для ![]() и наоборот.
и наоборот.
Пример 9.3. Определим радиус сходимости для z-преобразования сигнала, заданного в примере 9.2.
Как уже было установлено, z-преобразование сигнала ![]() имеет вид
имеет вид
![]() .
.
Нуль функции ![]() будет в точке
будет в точке ![]() , полюс – в точке
, полюс – в точке ![]() . Следовательно, радиус сходимости
. Следовательно, радиус сходимости ![]() , а функция
, а функция ![]() сходится при
сходится при ![]() .
.
Окружность, имеющая радиус сходимости ![]() , приведенана рис. 20. Область сходимости находится за пределами этой окружности.
, приведенана рис. 20. Область сходимости находится за пределами этой окружности.
Пример 9.4. Найдем z-преобразование сигнала ![]() , n ³ 0. Этот дискретный сигнал показан на рис. 22 для трех различных значений a: а = 0,8; а = 1; а = –0,8.
, n ³ 0. Этот дискретный сигнал показан на рис. 22 для трех различных значений a: а = 0,8; а = 1; а = –0,8.
В соответствии с (13) z-преобразование такого дискретного сигнала равно
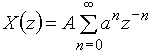 . (14)
. (14)
Из математики известно, что этот ряд сходится к функции
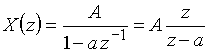 , (15)
, (15)
если ![]() или
или ![]() .
.
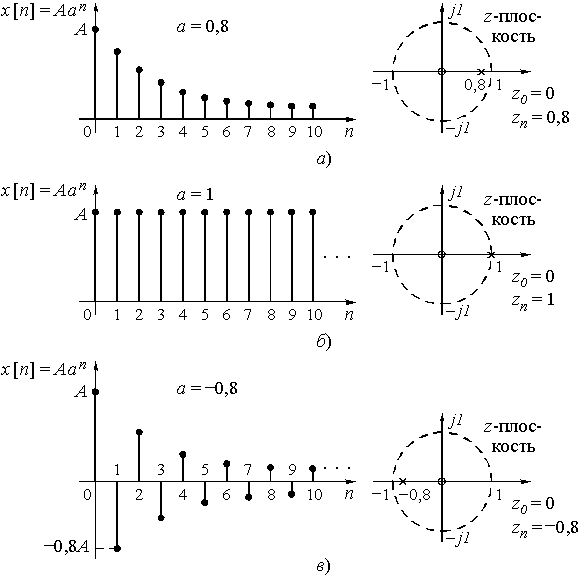
Рис. 22
Функция ![]() имеет нуль при z = 0, а ее полюс
имеет нуль при z = 0, а ее полюс ![]() лежит на окружности радиусом
лежит на окружности радиусом ![]() , ограничивающей область сходимости.
, ограничивающей область сходимости.
На рис. 22 показано расположение нуля и полюса функции ![]() в z-плоскости при различных а.
в z-плоскости при различных а.
Самоконтроль
1. Как рассчитать z-изображение дискретного сигнала?
2. Как связаны одностороннее z-преобразование и преобразование Лапласа?
3. Какие точки z-плоскости соответствуют точкам левой (правой) р-полуплоскости?
4. Что такое радиус сходимости?
5. Найдите z-изображение дискретного сигнала ![]() = {0; 1; 2; 3}.
= {0; 1; 2; 3}.
6. Найдите z-изображение дискретного сигнала ![]() .
.
7. Найдите радиус сходимости для z-преобразования сигнала ![]() .
.
Вопрос 10. Как найти дискретный сигнал по его z-преобразованию?
Можно воспользоваться обратным z-преобразованием (подобно тому как мы пользуемся обратным преобразованием Лапласа):
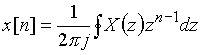 ,
,
где интегрирование ведется по замкнутому контуру в z-плоскости.
Другой способ заключается в том, чтобы разложить функцию ![]() в степенной ряд по степеням
в степенной ряд по степеням ![]() . Тогда коэффициенты при степенях
. Тогда коэффициенты при степенях ![]() будут, в соответствии с формулой (13), отсчетами дискретного сигнала
будут, в соответствии с формулой (13), отсчетами дискретного сигнала ![]() .
.
Пример 10.1. Найдем дискретный сигнал ![]() , которому соответствует z-преобразование
, которому соответствует z-преобразование 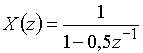 .
.
Воспользуемся разложением функции ![]() в ряд
в ряд ![]()
![]() .
.
Для заданного z-преобразования ![]() , поэтому запишем z-преобразование в виде
, поэтому запишем z-преобразование в виде
![]() .
.
Сравнивая полученное выражение с общей формулой z-преобразования 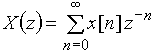 , записываем последовательность
, записываем последовательность
![]() {1; 0,5; 0,25; 0,125; ...}.
{1; 0,5; 0,25; 0,125; ...}.
Общий член этой последовательности ![]() .
.
Пример 10.2. Найдем отсчеты дискретного сигнала по его z-преобразованию
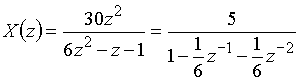 .
.
Для разложения функции ![]() в степенной ряд по степеням
в степенной ряд по степеням ![]() выполним деление числа 5 на многочлен
выполним деление числа 5 на многочлен 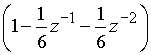 . В результате получим частное
. В результате получим частное ![]() . Отсчеты дискретного сигнала равны
. Отсчеты дискретного сигнала равны
![]() и т.д.
и т.д.
Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе ![]() , не слишком сложные.
, не слишком сложные.
Более эффективным способом нахождения ![]() по известному
по известному ![]() является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
Пример 10.3. Найдем общий член ![]() дискретного сигнала
дискретного сигнала ![]() , которому соответствует z-изображение, заданное в примере 10.2
, которому соответствует z-изображение, заданное в примере 10.2
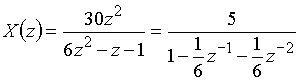 .
.
Функция ![]() имеет полюсы в точках
имеет полюсы в точках ![]() и
и ![]() , или, что то же, в точках
, или, что то же, в точках ![]() и
и ![]() .
.
Разложим ![]() на сумму простых дробей:
на сумму простых дробей:
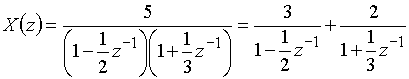 . (16)
. (16)
Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления ![]() реактивных двухполюсников при синтезе их по схеме Фостера:
реактивных двухполюсников при синтезе их по схеме Фостера:
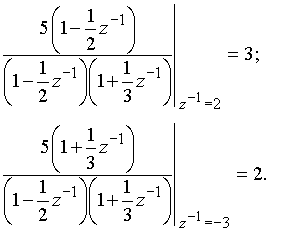
Подобно тому, как формула (15) представляет сумму ряда (14), простые дроби в (16) являются суммами рядов
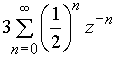 и
и 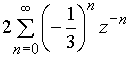 .
.
Поскольку z-преобразование – это линейная операция, то последовательность ![]() состоит из суммы двух последовательностей:
состоит из суммы двух последовательностей:
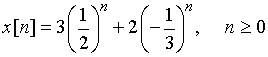 .
.
После выполнения операции возведения в степень n получим отсчеты дискретного сигнала
![]() и т.д.
и т.д.
Самоконтроль
1. Какие способы используются для нахождения дискретного сигнала по его z-преобразованию?
2. Запишите общий член последовательности ![]() , имеющей z-преобразование
, имеющей z-преобразование ![]() .
.
3. Запишите общий член последовательности ![]() , имеющей z-преобразование
, имеющей z-преобразование 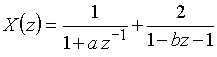 . Найдите значения
. Найдите значения ![]() ,
, ![]() и
и ![]() этой последовательности.
этой последовательности.
Вопрос 11. Какими свойствами обладает z-преобразование?
Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z-преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.
Теорема линейности (суперпозиции)
Сумме дискретных сигналов соответствует сумма их z-изображений. Если дискретным сигналам ![]() и
и ![]() соответствуют z-изображения
соответствуют z-изображения ![]() и
и ![]() , то
, то
![]() ,
,
где a и b - некоторые числа.
Доказательство теоремы выполните самостоятельно, используя выражение (13) для расчета z-изображения дискретного сигнала.
Теорема опережающего сдвига
Если дискретному сигналу ![]() соответствует одностороннее z-преобразование
соответствует одностороннее z-преобразование ![]() , то сигналу, сдвинутому на один интервал дискретизации,
, то сигналу, сдвинутому на один интервал дискретизации, ![]() соответствует z-преобразование
соответствует z-преобразование ![]() .
.
Математическая запись теоремы имеет вид
![]() ,
,
Чтобы доказать теорему, воспользуемся основным выражением (13) для расчета z-преобразования дискретных сигналов ![]() и
и ![]() , а также графиками, приведенными на рис. 23.
, а также графиками, приведенными на рис. 23.
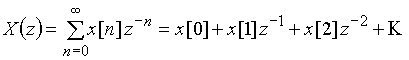 ;
;
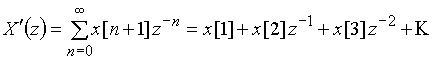 .
.
Сравнивая ![]() и
и ![]() , получаем
, получаем ![]() , что и требовалось доказать.
, что и требовалось доказать.
Очевидно, что теорема опережающего сдвига выполняет ту же самую роль, что и теорема дифференцирования для преобразований Лапласа.
Теорема задержки
Математическая запись теоремы имеет вид
![]() .
.
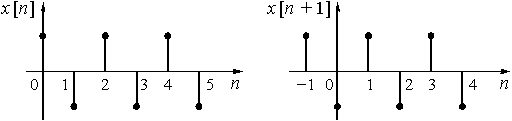
Рис. 23
В теореме задержки ![]() - это дискретные отсчеты функции единичного скачка (рис. 24)
- это дискретные отсчеты функции единичного скачка (рис. 24)
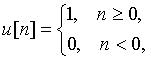
а ![]() - это дискретные отсчет функции
- это дискретные отсчет функции ![]() , задержанной на N интервалов дискретизации (рис. 25).
, задержанной на N интервалов дискретизации (рис. 25).
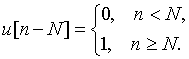
Доказательство вытекает из основного выражения (13) для z-преобразования.
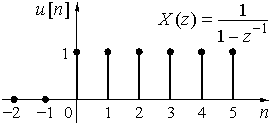
Рис. 24
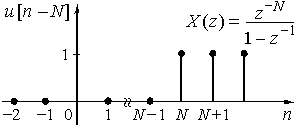
Рис. 25
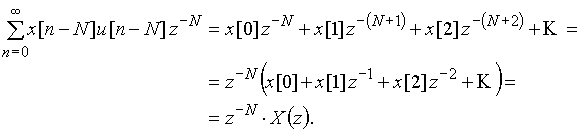
При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т.е. при n < N.
Теорема умножения на an
Математическая запись теоремы имеет вид
![]() .
.
Теорема умножения на n
![]() .
.
Теоремы умножения дискретного сигнала ![]() на
на ![]() и на n можно также доказать, используя формулу (13). Предлагаем проделать это самостоятельно.
и на n можно также доказать, используя формулу (13). Предлагаем проделать это самостоятельно.
Теорема свертки
Свертке дискретных сигналов ![]() и
и ![]() соответствует произведение их z-преобразований
соответствует произведение их z-преобразований
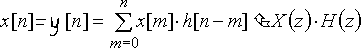 .
.
Эту теорему мы приводим здесь без доказательства. При необходимости с ним можно познакомиться в [6].
Пример 11.1. Найдем z-преобразование функции единичного отсчета, задержанной на N интервалов дискретизации.
Найдем z-преобразование дискретного d-импульса ![]() (рис. 3), используя выражение (13)
(рис. 3), используя выражение (13)
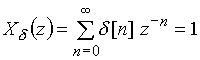 .
.
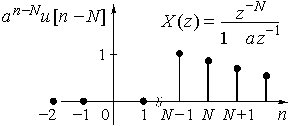
Рис. 26
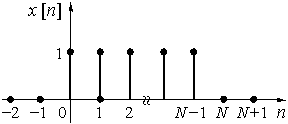
Рис. 27
Используя теорему задержки, найдем z-изображение сигнала ![]()
![]() .
.
На рисунке 3 приведен также график задержанной функции единичного отсчета для частного случая N = 2.
Пример 11.2. Найдем z-преобразование функции
![]() .
.
В примере 9.4 мы уже находили, что z-преобразование сигнала ![]() имеет вид (15)
имеет вид (15) 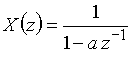 .
.
Используя теорему задержки, получаем
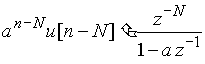 .
.
При a = 1 имеем:
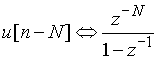 .
.
Графики дискретных сигналов ![]() и
и ![]() приведены на рис. 25 и 26.
приведены на рис. 25 и 26.
Пример 11.3. Найдем z-преобразование дискретной последовательности ![]() .
.
Поскольку z-изображение последовательности ![]() известно (15), то, используя теорему умножения на n, получим
известно (15), то, используя теорему умножения на n, получим
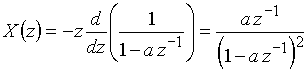 .
.
Пример 11.4. Найдем z-преобразование дискретной последовательности из N отсчетов единичной амплитуды (рис. 27)
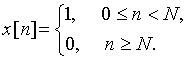
Сигнал ![]() можно представить как разность двух сигналов
можно представить как разность двух сигналов
![]() .
.
Из теорем линейности и задержки легко получить z-преобразование
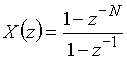 ,
,
что совпадает с формулой для частичной суммы геометрической прогрессии
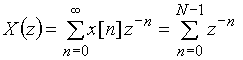 .
.
Пример 11.5. Вычислим z-преобразование свертки дискретных сигналов ![]() ={1; 1; 1; 0; 0; 0; ...} и
={1; 1; 1; 0; 0; 0; ...} и 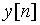 = {0; 0; 1; 1; 0; 0; ...}.
= {0; 0; 1; 1; 0; 0; ...}.
Найдем z-преобразование сигнала ![]() , используя формулу (13)
, используя формулу (13)
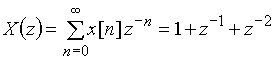 .
.
Найдем z-преобразование сигнала ![]()
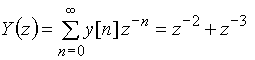 .
.
Вычислим z-преобразование свертки сигналов ![]() и
и ![]() , используя теорему свертки
, используя теорему свертки
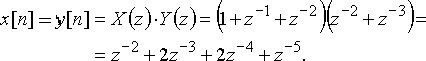
Табл. 1 - Краткая таблица односторонних z-преобразований
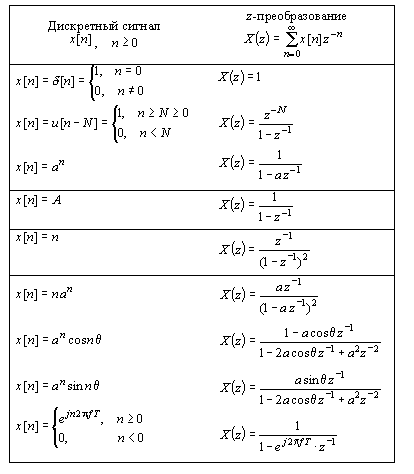
z-преобразование 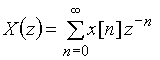
В табл. 1 дана сводка z-преобразований наиболее часто встречающихся дискретных последовательностей. Эти табличные сведения также могут быть использованы для расчета z-преобразований сигналов и перехода от z-преобразований к дискретным сигналам.
Пример 11.6. Найдем общий член дискретного сигнала ![]() , которому соответствует z-изображение
, которому соответствует z-изображение
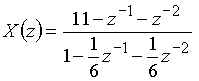 .
.
Разложение функции ![]() на простые дроби приводит к выражению
на простые дроби приводит к выражению
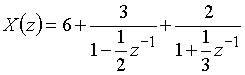 .
.
Используя теорему линейности и находя в таблице 1 дискретные сигналы, соответствующие каждому из слагаемых в выражении ![]() , получаем
, получаем
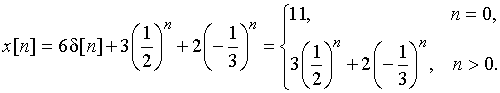
По этой формуле легко подсчитать значение ![]() для любого n. Аналогичным образом, разложение
для любого n. Аналогичным образом, разложение
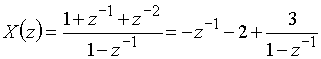
приводит к последовательности
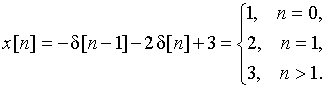
Самоконтроль
1. Докажите теорему линейности.
2. В чем суть теорем опережающего сдвига и задержки?
3. Сформулируйте теоремы умножения на ![]() и на n?
и на n?
4. Как найти z-преобразование свертки дискретных сигналов?
5. Как можно использовать таблицу односторонних z-преобразований?
Вопрос 12. Что такое дискретные цепи и чем они отличаются от аналоговых цепей?
Пример аналоговой цепи дан на рис. 6. Сигнал на ее выходе находят из интеграла свертки (наложения) по входному сигналу и импульсной характеристике. Формула интеграла свертки описывается выражением (1). Это выражение можно назвать математической моделью аналоговой цепи.
При переходе к дискретным сигналам используют выражение дискретной свертки (2). Обозначим в этом выражении
![]() .
.
Тогда оно запишется в виде
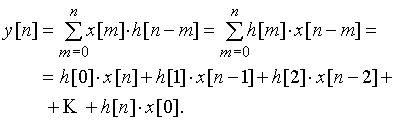 (17)
(17)
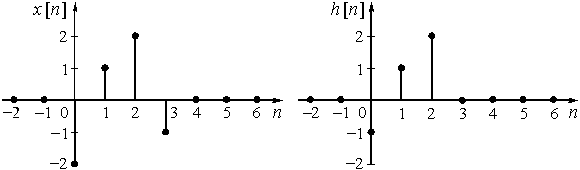
Рис. 28
Пример 12.1. Рассчитаем значения выходной последовательности ![]() цепи, имеющей дискретную импульсную характеристику
цепи, имеющей дискретную импульсную характеристику ![]() = {-1; 1; 2}, если входная последовательность имеет вид
= {-1; 1; 2}, если входная последовательность имеет вид ![]() = {-2; 1; 2: -1}. Графики
= {-2; 1; 2: -1}. Графики ![]() и
и ![]() приведены на рис. 28.
приведены на рис. 28.
Пользуясь формулой (17), рассчитаем значения выходной последовательности ![]()
![]()
![]()
![]()
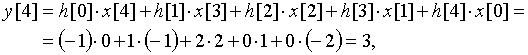
![]()
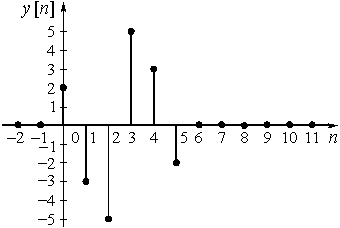
Рис. 29
График дискретного сигнала ![]() приведен на рис. 29.
приведен на рис. 29.
Вычисления по формуле (17) можно выполнить также с помощью простого устройства. Запишем последовательности чисел ![]() и
и ![]() на отдельных полосках бумаги, как показано на рис. 30. На обеих полосках пометим маленькими стрелочками точки n = 0. Обратим внимание на то, что
на отдельных полосках бумаги, как показано на рис. 30. На обеих полосках пометим маленькими стрелочками точки n = 0. Обратим внимание на то, что ![]() является обратной последовательностью относительно
является обратной последовательностью относительно ![]() , так что она строится в обратном направлении от n = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность
, так что она строится в обратном направлении от n = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность ![]() .
.
Если в качестве чисел ![]() взять дискретные значения
взять дискретные значения ![]()
![]() , то выражение (17) будет являться дискретной математической моделью аналоговой RC-цепи, изображенной на рис. 6. Выбирая те или иные значения
, то выражение (17) будет являться дискретной математической моделью аналоговой RC-цепи, изображенной на рис. 6. Выбирая те или иные значения ![]() , получим дискретные модели различных цепей. Таким образом, формула дискретной свертки является универсальной, пригодной для описания любых цепей.
, получим дискретные модели различных цепей. Таким образом, формула дискретной свертки является универсальной, пригодной для описания любых цепей.

Рис. 30
Пример 12.2. На вход цепи поступает сигнал в виде дискретной d-функции. Рассчитаем выходные последовательности ![]() цепей, имеющих дискретные импульсные характеристики
цепей, имеющих дискретные импульсные характеристики
а) ![]() = {1; 1; 0; 0; ...};
= {1; 1; 0; 0; ...};
б) ![]() = {1; -1; 0; 0; ...};
= {1; -1; 0; 0; ...};
в) ![]() .
.
Рис. 31
Графики дискретной d-функции ![]() и импульсных характеристик а), б), в) приведены на рис. 31 и рис. 32 соответственно.
и импульсных характеристик а), б), в) приведены на рис. 31 и рис. 32 соответственно.
Рассчитываем значения ![]() , используя формулу (17)
, используя формулу (17) ![]()
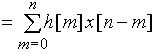 , в которой
, в которой ![]() =
= ![]() = {1; 1; 0; 0; ...}.
= {1; 1; 0; 0; ...}.
Для цепи, имеющей дискретную импульсную характеристику
а) ![]() = {1; 1; 0; 0; ...}, получаем
= {1; 1; 0; 0; ...}, получаем
![]()
![]()
![]()
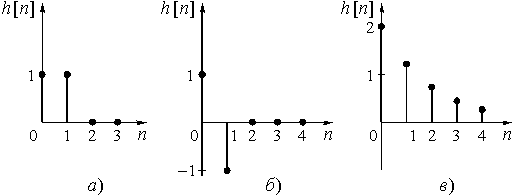
Рис. 32
![]()
Все остальные значения ![]() будут также нулевыми.
будут также нулевыми.
Для цепи с импульсной характеристикой
б) ![]() = {1; -1; 0; 0; ...} получаем
= {1; -1; 0; 0; ...} получаем
![]()
![]()
![]()
Остальные значения ![]() равны нулю.
равны нулю.
Для цепи с импульсной характеристикой
в) ![]() = {2; 1,22; 0, 74; 0,45; 0,27; ...} получаем
= {2; 1,22; 0, 74; 0,45; 0,27; ...} получаем
![]()
![]()
![]()
Все остальные отсчеты выходной последовательности ![]() повторяют соответствующие отсчеты дискретной импульсной характеристики
повторяют соответствующие отсчеты дискретной импульсной характеристики ![]() , также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т.к. импульсная характеристика - это реакция цепи на d-импульс.
, также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т.к. импульсная характеристика - это реакция цепи на d-импульс.
Графики ![]() будут такими же, как графики
будут такими же, как графики ![]() на рис. 32.
на рис. 32.
Анализ формулы (17) показывает, что в ней выполняется всего три действия: умножение, сложение и задержка. На рис. 33 эти действия представлены в виде элементов структурной схемы. Операцию умножения дискретного сигнала ![]() на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал
на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал ![]() . Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета
. Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета ![]() из
из ![]() можно связать с задержкой последнего на время Т, т.е. на один «такт».
можно связать с задержкой последнего на время Т, т.е. на один «такт».
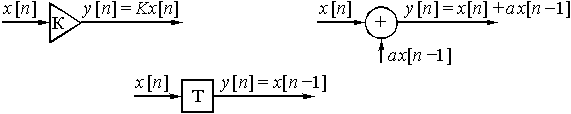
Рис. 33
Действие элемента задержки поясняется на рис. 34.
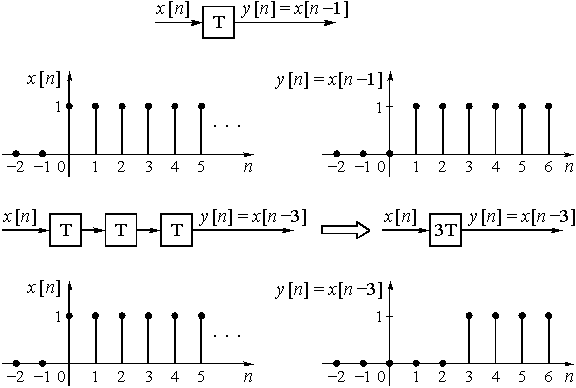
Рис. 34
Алгоритм вычислений дискретного сигнала ![]() , описываемый выражением (17), можно представить в виде структурной схемы. Подобные структурные схемы называют дискретными цепями.
, описываемый выражением (17), можно представить в виде структурной схемы. Подобные структурные схемы называют дискретными цепями.
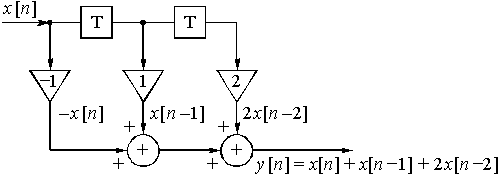
Рис. 35
Пример 12.3. Составим структурную схему цепи, дискретная импульсная характеристика которой дана в задаче 12.1, т.е. ![]() = {-1; 1; 2} (рис. 28).
= {-1; 1; 2} (рис. 28).
В соответствии с алгоритмом (17) и с учетом заданных значений характеристики ![]() структурная схема цепи приведена на рис. 35. По этой схеме несложно определить выражение для выходной последовательности
структурная схема цепи приведена на рис. 35. По этой схеме несложно определить выражение для выходной последовательности ![]()
![]() .
.
Вывод: в отличие от аналоговых цепей, которые представляют собой соединение элементов, например, R, L и С, дискретная цепь - это структурная схема алгоритма вычислений выходной последовательности по входной. Она состоит из элементов задержки, сумматоров и усилителей (умножителей).
Самоконтроль
1. В чем отличие импульсных характеристик дискретных и аналоговых цепей?
2. Как вычисляются значения выходной последовательности дискретной цепи?
3. Какие дискретные элементы используются для реализации алгоритма дискретной свертки?
4. Как работает элемент задержки? Приведите структурную схему цепи, на вход которой подается дискретный сигнал ![]() , а на выходе сигнал
, а на выходе сигнал ![]() .
.
5. Составьте структурные схемы дискретных цепей, имеющих дискретные импульсные характеристики, приведенные в примере 12.2, а и 12.2, б.
6. Запишите общие выражения выходных последовательностей ![]() для каждой из дискретных цепей, полученных в предыдущем пункте 5.
для каждой из дискретных цепей, полученных в предыдущем пункте 5.
Вопрос 13. Что такое цифровые цепи и чем они отличаются от дискретных цепей?
Приведенные на рис. 34 и 35 операции можно осуществить с помощью элементов цифровой или вычислительной техники. Первые представляют собой выпускаемые промышленностью интегральные микросхемы, позволяющие задерживать, складывать и умножать сигналы, последние - это серийные макро-, мини- и микро-ЭВМ, либо микропроцессорные устройства.
Характерно, что и те и другие средства работают с цифровыми сигналами (см. рис. 8), т.е. с отсчетами, представленными в двоичном коде. В этом случае любая конкретная цепь (например, рис. 35) может быть реализована с помощью устройства, собранного из интегральных микросхем, либо в виде программы в ЭВМ или в микропроцессорном устройстве.
Заметим, что представление чисел в двоичном коде из-за ограниченности разрядности цифровых устройств выполняется неточно. Операция умножения отсчетов цифрового сигнала на число также выполняется неточно из-за округления или усечения результата. Это приводит к ошибкам при восстановлении непрерывных сигналов. Существует только один путь уменьшения этих ошибок - увеличение количества разрядов в двоичном коде.
Вывод: если дискретная цепь - это структурная схема алгоритма вычислений, то цифровая цепь - это воплощение данного алгоритма в виде аппаратных и программных средств.
Самоконтроль
1. Что такое цифровые сигналы?
2. Как реализовать цепь для обработки цифровых сигналов?
3. Почему возникают ошибки при восстановлении непрерывного сигнала по его цифровому представлению? Как их уменьшить?
4. В чем отличие цифровой и дискретной цепей?
Вопрос 14. Как определять передаточную функцию дискретной цепи?
Рассмотрим один из элементов дискретной цепи - элемент задержки (рис. 34). Сигнал на его входе ![]() , а на выходе
, а на выходе ![]() . Напомним, что z-изображения дискретных сигналов
. Напомним, что z-изображения дискретных сигналов ![]() и
и ![]() имеют вид:
имеют вид:
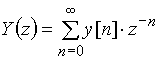 ,
, 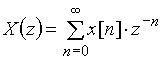 .
.
Тогда, воспользовавшись теоремой задержки, можно записать z-преобразование для равенства ![]() :
:
![]() .
.
Отношение z-изображений выходного и входного дискретных сигналов называют передаточной (или системной) функцией дискретной цепи ![]() :
:
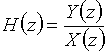 .
.
Тогда ![]() .
.
В таком случае передаточная функция элемента задержки:
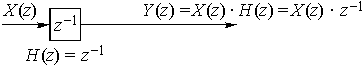
Рис. 36
![]() (рис. 36).
(рис. 36).
Обратимся теперь к выражению (17). На основании теоремы свертки z-преобразование дискретной свертки равно произведению z-преобразований дискретных сигналов:
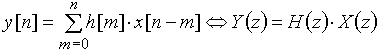 .
.
Из последнего выражения видно, что z-преобразование дискретной импульсной реакции ![]() есть передаточная функция
есть передаточная функция ![]() дискретной цепи:
дискретной цепи:
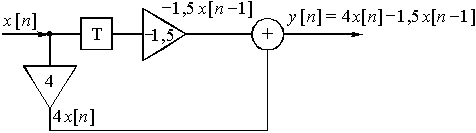
Рис. 37
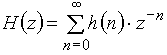 .
.
Пример 14.1. Найдем импульсную характеристику и передаточную функцию дискретной цепи (рис. 37), выходная последовательность которой задана выражением ![]() .
.
Отсчеты дискретной импульсной характеристики ![]() - это отсчеты
- это отсчеты ![]() , рассчитанные при условии, что на вход цепи подается дискретная d-функция, т.е.
, рассчитанные при условии, что на вход цепи подается дискретная d-функция, т.е. ![]() = {1; 0; 0; ...}.
= {1; 0; 0; ...}.
![]() ,
,
![]() ,
,
![]() при n> 1.
при n> 1.
Таким образом, отсчеты дискретной импульсной характеристики ![]() = {4; -1,5} соответствуют коэффициентам усиления усилителей в схеме (рис. 37).
= {4; -1,5} соответствуют коэффициентам усиления усилителей в схеме (рис. 37).
Для нахождения передаточной функции ![]() возьмем z-преобразование дискретной импульсной характеристики
возьмем z-преобразование дискретной импульсной характеристики
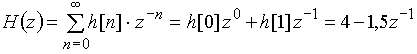 .
.
Другой способ нахождения передаточной функции ![]() заключается в том, чтобы определить z-изображение выходной последовательности, а затем найти
заключается в том, чтобы определить z-изображение выходной последовательности, а затем найти ![]() как отношение
как отношение ![]() и
и ![]() :
:
![]()
или
![]() .
.
Очевидно, что ![]() . Z-изображение дискретной цепи с такой передаточной функцией приведено на рис. 38.
. Z-изображение дискретной цепи с такой передаточной функцией приведено на рис. 38.
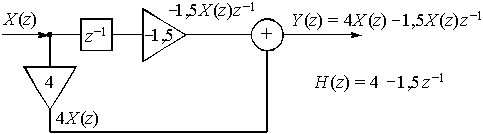
Рис. 38
Пример 14.2. Найдем отсчеты выходного сигнала ![]() дискретной цепи, z-изображение которой приведено на рис. 39, а входной сигнал
дискретной цепи, z-изображение которой приведено на рис. 39, а входной сигнал ![]() = {-2; 1; 2; -1}.
= {-2; 1; 2; -1}.
Найдем z-изображение входного сигнала ![]() :
:
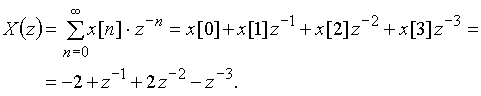
Передаточная функция цепи (рис. 39) ![]() . Она находится непосредственно по схеме либо как z-изображение дискретной импульсной характеристики
. Она находится непосредственно по схеме либо как z-изображение дискретной импульсной характеристики ![]() = {-1; 1; 2}.
= {-1; 1; 2}.
Найдем z-изображение выходного сигнала
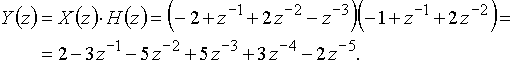
Коэффициенты при z в отрицательных степенях в этом выражении являются отсчетами выходного сигнала ![]() (рис. 29):
(рис. 29):
![]() = {2; -3; -5; 5; 3; -2}.
= {2; -3; -5; 5; 3; -2}.
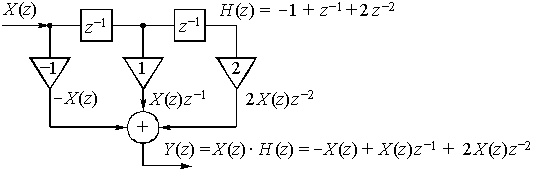
Рис. 39
Пример 14.3. Найдем передаточную функцию дискретной цепи, входная и выходная последовательности которой имеют вид
![]() = {1; 0; 1; 2},
= {1; 0; 1; 2}, ![]() = {0; 1; 2; 1}.
= {0; 1; 2; 1}.
Z-изображения последовательностей
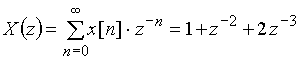 ;
;
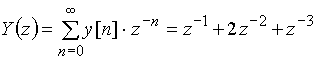 .
.
Следовательно, передаточная функция
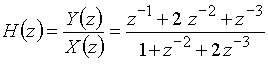 .
.
Разделив числитель передаточной функции на знаменатель, можно представить ![]() в виде
в виде
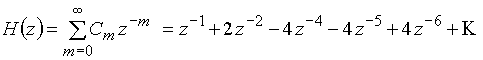 .
.
Самоконтроль
1. Что такое передаточная функция дискретной цепи?
2. Чему равна передаточная функция элемента задержки?
3. Как связаны передаточная функция и импульсная характеристика дискретной цепи?
4. Найдите передаточную функцию дискретной цепи, если ![]() = = {1; 1; 1},
= = {1; 1; 1}, ![]() = {0; 0; 1}.
= {0; 0; 1}.
5. Найдите передаточную функцию цепи, дискретная импульсная характеристика которой имеет вид ![]() = {1; -2; 3}.
= {1; -2; 3}.
6. Приведите структурную схему цепи, имеющей передаточную функцию ![]() .
.
Вопрос 15. Что такое нерекурсивные и рекурсивные дискретные цепи?
Рассмотрим структуру дискретной цепи, подобную рис. 35 и 39, но содержащую N элементов задержки. Она приведена на рис. 40,а и б. Здесь коэффициенты усиления ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() представляют собой отсчеты дискретной импульсной реакции
представляют собой отсчеты дискретной импульсной реакции ![]() , т.е.
, т.е.
![]() .
.
Из структуры рис. 40,а следует, что
![]() . (18)
. (18)
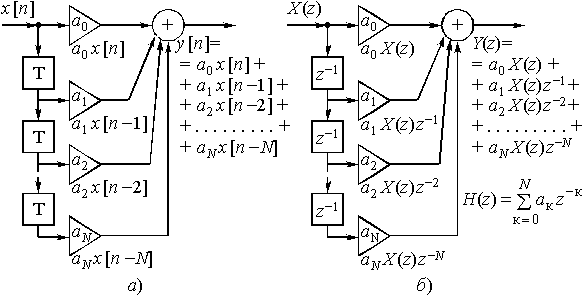
Рис. 40
Переход к z-изображениям (рис. 40, б) дает выражение:
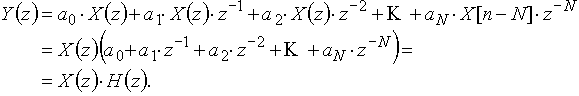
Передаточная функция этой дискретной цепи есть
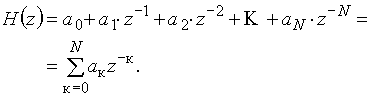 (19)
(19)
Дискретные цепи со структурой рис. 40,а и б и передаточной функцией вида (19) называются нерекурсивными цепями.
Пример 15.1. Найдем выходную последовательность и передаточную функцию нерекурсивной цепи, структурная схема которой приведена на рис. 41.
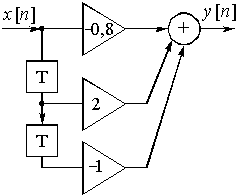
Рис. 41
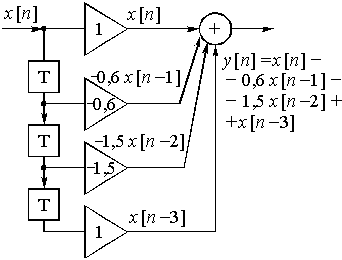
Рис. 42
Выходная последовательность ![]() в соответствии с уравнением (18) имеет вид
в соответствии с уравнением (18) имеет вид
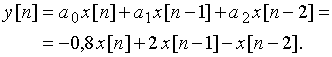
Передаточную функцию цепи найдем, используя уравнение (19) или непосредственно по схеме
![]() .
.
Пример 15.2. Найдем отсчеты выходного сигнала нерекурсивной дискретной цепи, имеющей дискретную импульсную реакцию ![]() = {1; -0,6; -1,5; 1}, при воздействии не нее дискретного сигнала
= {1; -0,6; -1,5; 1}, при воздействии не нее дискретного сигнала ![]() = {1; 0; 1; 0}.
= {1; 0; 1; 0}.
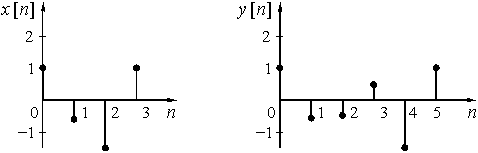
Рис. 43
Отсчеты дискретной импульсной характеристики - это коэффициенты усиления ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Структурная схема нерекурсивной дискретной цепи с заданной импульсной реакцией приведена на рис. 42.
. Структурная схема нерекурсивной дискретной цепи с заданной импульсной реакцией приведена на рис. 42.
Выходной дискретный сигнал ![]() найдем, используя выражение (19)
найдем, используя выражение (19)
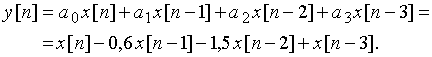
Отсчеты сигнала ![]() найдем, подставляя значения
найдем, подставляя значения ![]() в полученное разностное уравнение.
в полученное разностное уравнение.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Аналогичным образом рассчитываем ![]() ;
; ![]() ;
; ![]() . Все остальные отсчеты также равны нулю.
. Все остальные отсчеты также равны нулю.
Таким образом, выходная последовательность![]() = {1; -0,6; -0,5; 0,4; -1,5; 1}. Графики
= {1; -0,6; -0,5; 0,4; -1,5; 1}. Графики ![]() и
и ![]() приведены на рис. 43.
приведены на рис. 43.
Иного рода дискретная цепь показана на рис. 44,а и б.
Как следует из (рис. 44,а), выходной сигнал
![]() . (20)
. (20)
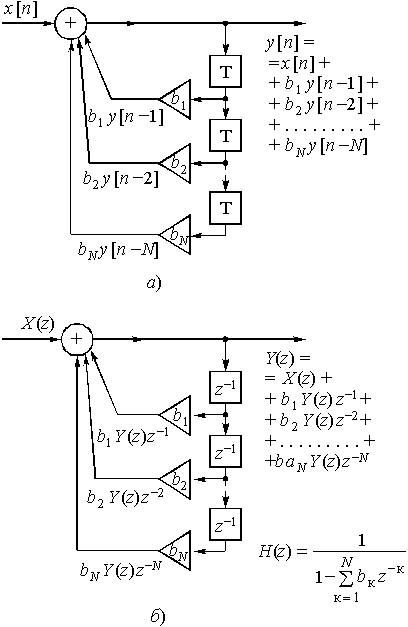
Рис. 44
Формула (20) позволяет вычислить текущий отсчет ![]() выходного сигнала не только по текущему отсчету
выходного сигнала не только по текущему отсчету ![]() входного сигнала, но и по предыдущим (задержанным) N отсчетам
входного сигнала, но и по предыдущим (задержанным) N отсчетам ![]() ,
, ![]() , ...,
, ..., ![]() выходного сигнала. Подобные формулы, в отличие от (18), где используются текущий и задержанные отсчеты только входного сигнала, в математике получили название рекурсивных. Поэтому и цепь, реализующая алгоритм (20), называется рекурсивной.
выходного сигнала. Подобные формулы, в отличие от (18), где используются текущий и задержанные отсчеты только входного сигнала, в математике получили название рекурсивных. Поэтому и цепь, реализующая алгоритм (20), называется рекурсивной.
Z-преобразование выражения (20) имеет вид:
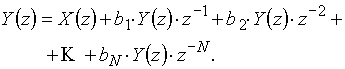 (21)
(21)
Эта же запись следует непосредственно из рис. 44,б.
Передаточную функцию рекурсивной цепи получаем из (21):
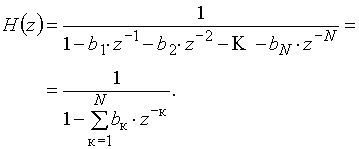 (22)
(22)
Пример 15.3. Структурная схема рекурсивной дискретной цепи приведена на рис. 45. Найдем передаточную функцию, импульсную характеристику и реакцию цепи на дискретное воздействие ![]() = {1; -1; 1}.
= {1; -1; 1}.
Передаточную функцию цепи ![]() найдем, используя формулу (22)
найдем, используя формулу (22)
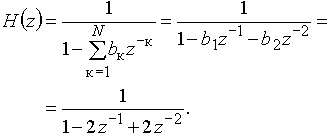
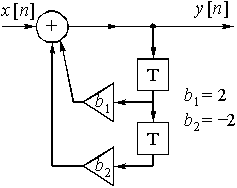
Рис. 45
Для нахождения дискретной импульсной характеристики ![]() рассчитаем реакцию цепи
рассчитаем реакцию цепи ![]() на дискретную d-функцию, т.е. на сигнал
на дискретную d-функцию, т.е. на сигнал ![]() =
= ![]() = {1; 0; 0; ...}. С учетом формулы (20) получаем, что дискретная импульсная характеристика цепи (рис. 45) имеет вид
= {1; 0; 0; ...}. С учетом формулы (20) получаем, что дискретная импульсная характеристика цепи (рис. 45) имеет вид
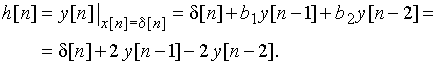
Отсчеты ![]() равны соответственно
равны соответственно ![]() = 1;
= 1; ![]() = 2;
= 2;![]() = = 2;
= = 2; ![]() = 0 и т.д.
= 0 и т.д.
Для расчета реакции цепи ![]() на сигнал
на сигнал ![]() также воспользуемся разностным уравнением (20):
также воспользуемся разностным уравнением (20):
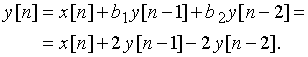
Найдем отсчеты ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
; ![]() и т.д.
и т.д.
Если выход дискретной цепи рис. 40,а подключить ко входу цепи, изображенной на рис. 44,а, то полученная цепь будет описываться уравнением
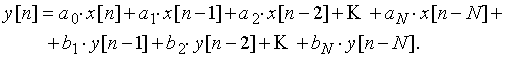 (23)
(23)
Для получения передаточной функции ![]() можно либо выполнить z-преобразование выражения (23), либо перемножить передаточные функции (19) и (22) каскадно включенных структур:
можно либо выполнить z-преобразование выражения (23), либо перемножить передаточные функции (19) и (22) каскадно включенных структур:
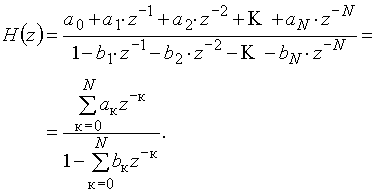 (24)
(24)
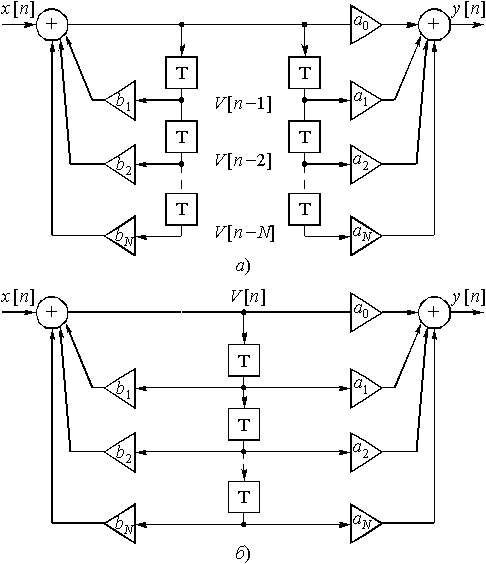
Рис. 46
Можно изменить порядок каскадного включения нерекурсивной и рекурсивной цепей на обратный. Получится схема, показанная на рис. 46,а. Передаточная функция этой новой структуры, естественно, будет по-прежнему описываться выражением (24), а временной алгоритм - формулой (23). Заметим, что на выходах параллельных элементов задержки будут одни и те же сигналы. Следовательно, реально необходимо иметь лишь один из двух элементов задержки. Соответствующая эквивалентная дискретная цепь изображена на рис. 46, б; она называется канонической, потому что в ней используется минимально возможное число элементов задержки. Так как схема рис. 46,б содержит и рекурсивную часть, в литературе ее часто также называют рекурсивной дискретной цепью.
Пример 15.4. Определим передаточную функцию цепи, приведенной на рис. 47.
Для рекурсивной цепи с прямыми и обратными связями (рис. 47) запишем коэффициенты усиления усилителей:
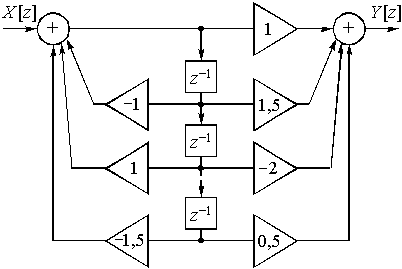
Рис. 47
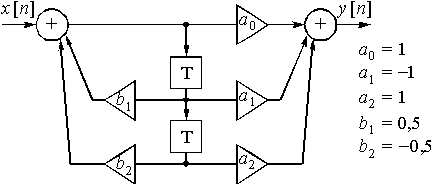
Рис. 48
![]() = 1;
= 1; ![]() = 1,5;
= 1,5; ![]() = -2;
= -2; ![]() = 0,5;
= 0,5;
![]() = -1;
= -1; ![]() = 1;
= 1; ![]() = -1,5.
= -1,5.
Определим передаточную функцию цепи (рис. 47), подставляя значения коэффициентов усиления в выражение (24),
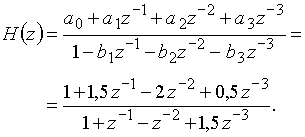
Пример 15.5. Найдем реакцию дискретной цепи на воздействие ![]() = {1; -1; 1; -1}, если передаточная функция цепи имеет вид
= {1; -1; 1; -1}, если передаточная функция цепи имеет вид 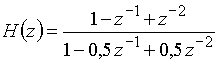 .
.
Составим структурную схему дискретной цепи с заданной передаточной функцией (рис. 48). Коэффициенты усиления известны: ![]() = 1;
= 1; ![]() = -1;
= -1; ![]() = 1;
= 1; ![]() = 0,5;
= 0,5; ![]() = -0,5.
= -0,5.
Найдем выходной сигнал ![]() цепи, используя уравнение (23) или непосредственно по схеме:
цепи, используя уравнение (23) или непосредственно по схеме:
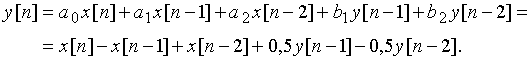
Рассчитаем отсчеты ![]() :
:
![]() ;
;
![]() ;
;
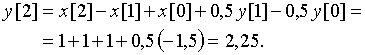
Аналогичным образом рассчитываем ![]() ,
, ![]()
![]() и т.д.
и т.д.
Самоконтроль
1. Какие дискретные цепи называются нерекурсивными?
2. Какие дискретные цепи называются рекурсивными?
3. Как рассчитываются передаточные функции нерекурсивных и рекурсивных дискретных цепей?
4. Как рассчитывается выходной сигнал дискретной цепи?
5. Составьте схемы дискретных цепей, имеющих передаточные функции
а) ![]() ;
;
б) 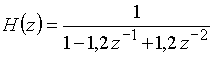 ;
;
в) 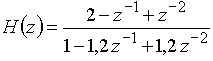 ;
;
г) 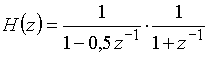 .
.
6. Запишите разностные уравнения для цепей, имеющих передаточные функции, приведенные в 5, а; 5, б и 5, в.
Вопрос 16. Где располагаются полюсы передаточной функции устойчивой дискретной цепи?
Дискретная цепь считается неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на ее выходе бесконечно нарастающий отклик. Наоборот, дискретная цепь устойчива когда отклик на ограниченное воздействие также ограничен.
Известно, что у устойчивой аналоговой цепи полюсы передаточной функции располагаются в левой полуплоскости переменной p. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа z-преобразованием точки левой полуплоскости p-плоскости переходят в точки, лежащие внутри единичной окружности z-плоскости (рис. 20). Таким образом, полюсы передаточной функции устойчивой дискретной цепи располагаются внутри единичной окружности z-плоскости.
Пример 16.1. Определим устойчивость цепей, имеющих передаточные функции:
а) 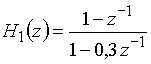 ,
,
б) 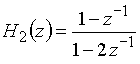 ,
,
в) 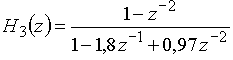 ,
,
г) 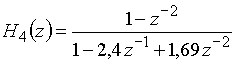 .
.
Полюс передаточной функции
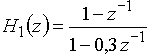
найдем, приравняв знаменатель ![]() к нулю,
к нулю, ![]() = 0.
= 0.
Получаем полюс ![]() = 0,3, который находится внутри единичной окружности z-плоскости. Это означает, что цепь устойчива.
= 0,3, который находится внутри единичной окружности z-плоскости. Это означает, что цепь устойчива.
Передаточная функция
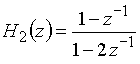
имеет полюс в точке ![]() = 2; такая цепь неустойчива.
= 2; такая цепь неустойчива.
Полюсы передаточной функции
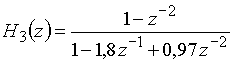
являются комплексно-сопряженными ![]() и
и ![]()
![]() . Поскольку эти полюсы лежат внутри единичной окружности (их модули
. Поскольку эти полюсы лежат внутри единичной окружности (их модули ![]() ), то данная дискретная цепь устойчива.
), то данная дискретная цепь устойчива.
Примером неустойчивой цепи служит цепь с передаточной функцией
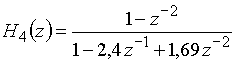 ,
,
у которой ![]() и
и ![]() и
и ![]() .
.
Пример 16.2. Дискретная цепь, являющаяся фильтром верхних частот с ослаблением в полосе непропускания (0 ¸ 500 Гц) более 36 дБ и с неравномерностью ослабления в полосе пропускания (выше 600 Гц) 1,25 дБ, при частоте дискретизации ![]() = 2,5 кГц имеет передаточную функцию
= 2,5 кГц имеет передаточную функцию
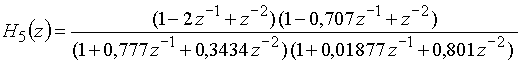 .
.
Ее полюсы ![]() и
и ![]() также лежат внутри области устойчивости. Заметим, что на нули таких ограничений нет: они оказались в точках z = 1 (двойной нуль) и
также лежат внутри области устойчивости. Заметим, что на нули таких ограничений нет: они оказались в точках z = 1 (двойной нуль) и ![]() , т.е. лежат на единичной окружности.
, т.е. лежат на единичной окружности.
Пример 16.3. Цифровой фильтр Баттерворта нижних частот 3-го порядка описывается передаточной функцией
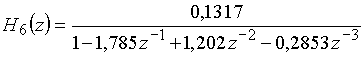 (25)
(25)
с полюсами ![]() и
и ![]() . Расположение полюсов в плоскости z показано на рис. 49, а). Здесь же приведена структурная схема такого фильтра (рис. 49, б). Цепь устойчива.
. Расположение полюсов в плоскости z показано на рис. 49, а). Здесь же приведена структурная схема такого фильтра (рис. 49, б). Цепь устойчива.
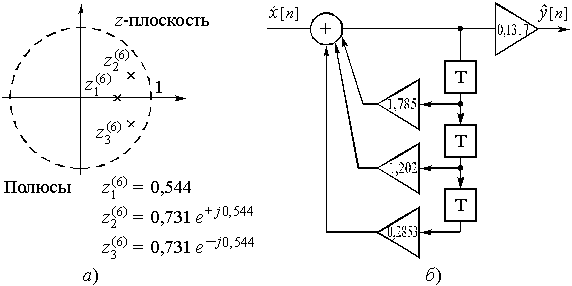
Рис. 49
Пример 16.4. Рассчитаем сигнал ![]() на выходе дискретной цепи, имеющей передаточную функцию
на выходе дискретной цепи, имеющей передаточную функцию 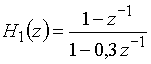 (см. Пример 16.1, а), если на вход подается сигнал
(см. Пример 16.1, а), если на вход подается сигнал ![]() = {3; 2; 1}.
= {3; 2; 1}.
Воспользуемся выражениями (23) и (24) для нахождения выходного сигнала ![]() в рекурсивной дискретной цепи с прямыми и обратными связями:
в рекурсивной дискретной цепи с прямыми и обратными связями:
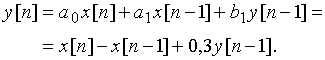
Рассчитаем значения выходного сигнала, подставляя значения ![]() в выражение для
в выражение для ![]() . Получаем выходную последовательность
. Получаем выходную последовательность ![]() = {3; -0,1; -1,03; -1,31: -0,39; -0,11; -0,03; -0,01; ...}. Таким образом, отклик
= {3; -0,1; -1,03; -1,31: -0,39; -0,11; -0,03; -0,01; ...}. Таким образом, отклик ![]() цепи с передаточной функцией
цепи с передаточной функцией ![]() на ограниченное воздействие также ограничен, т.е. цепь является устойчивой.
на ограниченное воздействие также ограничен, т.е. цепь является устойчивой.
Вывод: полюсы передаточной функции устойчивой дискретной цепи лежат внутри единичной окружности z-плоскости. Нерекурсивные цепи всегда устойчивы.
Самоконтроль
1. Какая дискретная цепь является устойчивой (неустойчивой)?
2. Где расположены полюсы передаточной функции устойчивой дискретной цепи?
3. Что можно сказать об устойчивости цепей с передаточными функциями
а) ![]() ,
,
б) 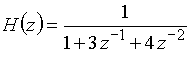 ,
,
в) 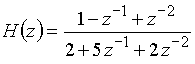 ?
?
Вопрос 17. Как построить амплитудно-частотную характеристику дискретной цепи?
При переходе от преобразования Фурье к z-преобразованию была сделана замена
![]() .
.
Для перехода от передаточной функции ![]() к частотной характеристике
к частотной характеристике ![]() необходимо произвести обратную замену
необходимо произвести обратную замену
![]() .
.
Обычно вводят в рассмотрение нормированную частоту W = f × T = ![]() . С учетом этого формула (24) примет вид:
. С учетом этого формула (24) примет вид:
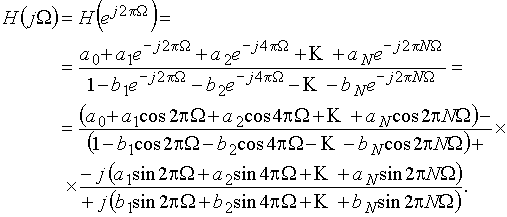 (26)
(26)
Из (26) легко получить амплитудно-частотную и фазо-частотную характеристики дискретной цепи. В частности, амплитудно-частотная характеристика будет представлена выражением
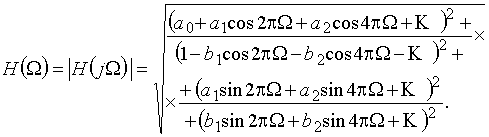 (27)
(27)
Пример 17.1. Рассмотрим цифровой фильтр Баттерворта нижних частот, приведенный на рис. 49,б и описываемый передаточной функцией (25). Подстановка в (25) ![]() дает
дает
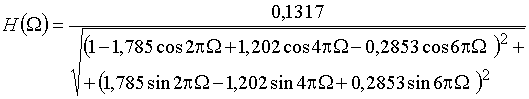 .
.
На рис. 50 изображен график АЧХ ![]() этого фильтра. Как и следовало ожидать, амплитудно-частотная характеристика дискретной цепи является периодической функцией (так как
этого фильтра. Как и следовало ожидать, амплитудно-частотная характеристика дискретной цепи является периодической функцией (так как ![]() есть преобразование Фурье от дискретной импульсной реакции). Ее период равен
есть преобразование Фурье от дискретной импульсной реакции). Ее период равен ![]() или
или ![]() . Поэтому она используется в диапазоне частот от 0 до
. Поэтому она используется в диапазоне частот от 0 до ![]() (или до W = 0,5).
(или до W = 0,5).
Пример 17.2. Найдем частотную характеристику цифрового фильтра с импульсной характеристикой ![]() = {1,5; 1; 0,5}.
= {1,5; 1; 0,5}.
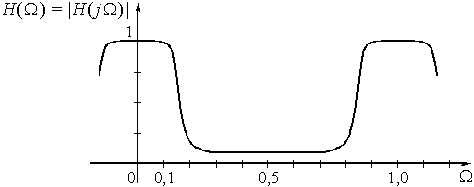
Рис. 50
Запишем передаточную функцию ![]() цифрового фильтра, воспользовавшись формулой
цифрового фильтра, воспользовавшись формулой 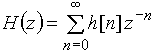 . Получим
. Получим ![]()
![]() передаточную функцию нерекурсивного фильтра.
передаточную функцию нерекурсивного фильтра.
Найдем АЧХ этого фильтра, подставляя в формулу (27) значения коэффициентов усиления ![]() ;
; ![]() ;
; ![]() ,
,
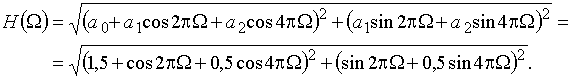
График АЧХ изображен на рис. 51.
Пример 17.3. Изменим коэффициенты усиления в предыдущем примере. Выберем ![]() ,
, ![]() . Вновь найдем выражение
. Вновь найдем выражение ![]() и построим график его амплитудно-частотной характеристики.
и построим график его амплитудно-частотной характеристики.
Заменим в формуле для ![]() , полученной в Примере 17.2, значения коэффициентов
, полученной в Примере 17.2, значения коэффициентов ![]() ,
, ![]() и
и ![]() . Получим
. Получим
![]() .
.
График АЧХ изображен на рис. 52. Из графика видно, что нерекурсивная цепь с такими значениями коэффициентов усиления - это режекторный фильтр.
Сопоставляя результаты расчета и графики, приведенные в Примерах 17.2 и 17.3, можно сделать важный вывод. Одним из основных преимуществ цифровых фильтров является простота их перестройки. Для получения фильтров разного функционального назначения достаточно изменить коэффициенты усиления.
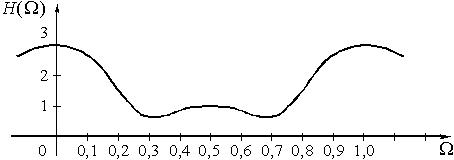
Рис. 51
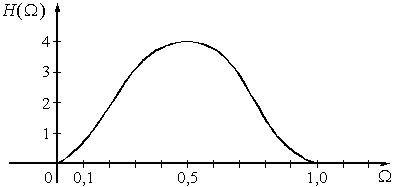
Рис. 52
Самоконтроль
1. Как перейти от передаточной функции к частотной характеристике?
2. Как определить амплитудно-частотную и фазо-частотную характеристики дискретной цепи?
3. Запишите выражение для амплитудно-частотной характеристики цепи, разностное уравнение которой имеет вид ![]()
![]() .
.
Вопрос 18. Существуют ли типовые звенья дискретных цепей?
Да, существуют. В литературе типовыми звеньями дискретных цепей считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры рис. 46, если оставить в ней только один либо два элемента задержки.
На рис. 53,а показано звено 1-го порядка с передаточной функцией
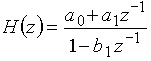
и АЧХ
 .
.
Типовое звено 2-го порядка изображено на рис. 53,б. Его передаточная функция
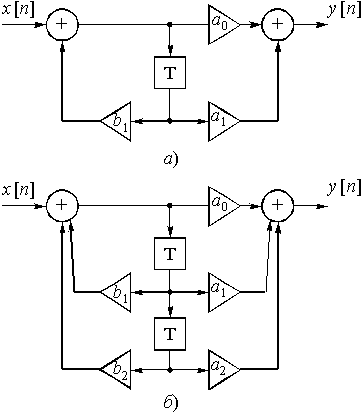
Рис. 53
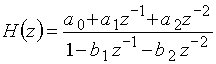
и АЧХ
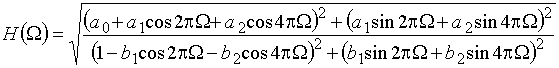 .
.
Пример 18.1. Построим график АЧХ звена первого порядка, у которого ![]() ,
, ![]() .
.
Передаточная функция такого звена первого порядка
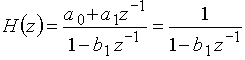 .
.
Амплитудно-частотная характеристика
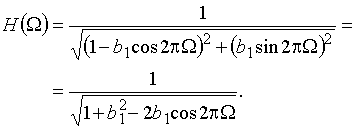
Поскольку полюс ![]() передаточной функции
передаточной функции ![]() равен
равен ![]() , то для того, чтобы цепь была устойчивой необходимо выбирать значения
, то для того, чтобы цепь была устойчивой необходимо выбирать значения ![]() такими, чтобы выполнялось условие
такими, чтобы выполнялось условие ![]() .
.
На рис. 54 приведены графики АЧХ, построенные для значений ![]() = 0,5 и
= 0,5 и ![]() = -0,5.
= -0,5.
АЧХ рассматриваемого фильтра зависит от знака коэффициента ![]() . При
. При ![]() > 0 получаем режекторный фильтр, при
> 0 получаем режекторный фильтр, при ![]() < 0 - полосовой.
< 0 - полосовой.
Пример 18.2. Найдем передаточную функцию и построим график АЧХ звена 2-го порядка (рис. 52,б) при ![]() ,
, ![]() ,
, ![]() = 0,2 и
= 0,2 и ![]() = -0,4.
= -0,4.
Передаточная функция такого звена
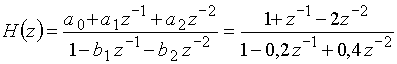 .
.
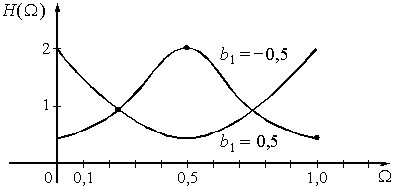
Рис. 54
Как указывалось ранее (Вопрос 15), рекурсивную цепь с прямыми и обратными связями можно представить как каскадное соединение рекурсивного фильтра с передаточной функцией ![]() и нерекурсивного фильтра с передаточной функцией
и нерекурсивного фильтра с передаточной функцией ![]() . В нашем случае, для звена второго порядка,
. В нашем случае, для звена второго порядка,
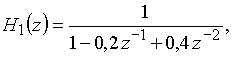
![]()
![]()
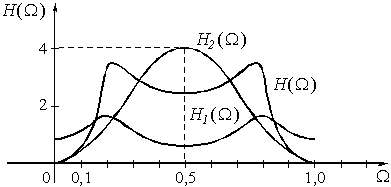
Рис. 55
График АЧХ для ![]() уже был построен и приведен на рис. 52. АЧХ
уже был построен и приведен на рис. 52. АЧХ ![]() рекурсивного фильтра рассчитывается по формуле
рекурсивного фильтра рассчитывается по формуле
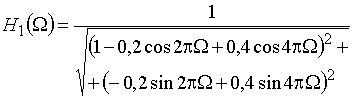 .
.
Графики ![]() ,
, ![]() и
и ![]() изображены на рис. 55.
изображены на рис. 55.
Самоконтроль
1. Какова структура звеньев 1-го и 2-го порядков дискретных цепей?
2. Как рассчитываются передаточные функции типовых звеньев дискретных цепей?
3. Запишите выражения для выходных напряжений ![]() звеньев 1-го и 2-го порядков.
звеньев 1-го и 2-го порядков.
Вопрос 19. Как соединяются между собой типовые звенья?
Типовые звенья могут соединяться каскадно (рис. 56,а); при этом их передаточные функции перемножаются:
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() - передаточные функции звеньев.
- передаточные функции звеньев.
При параллельном соединении звеньев (рис. 56,б) общая передаточная функция определяется как
![]() .
.
Соединение, показанное на рис. 56,в, называют включением цепи ![]() в обратную связь цепи
в обратную связь цепи ![]() , причем
, причем
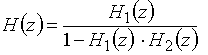 .
.
Следует иметь в виду, что все соединения, изображенные на рис. 56, справедливы не только для типовых звеньев, но и для любых других структур.
Пример 19.1. Найдем передаточные функции при различных способах соединения рекурсивной и нерекурсивной цепей, имеющих 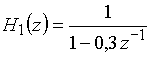 и
и ![]() .
.
При каскадном соединении этих цепей
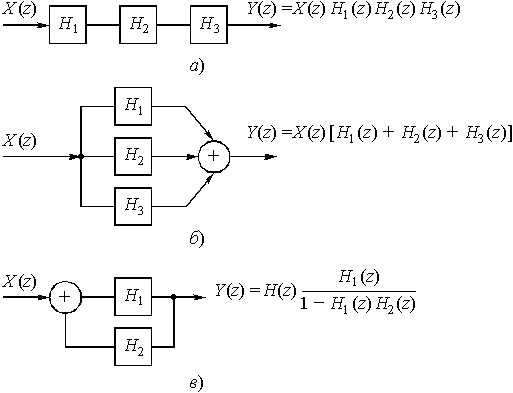
Рис. 56
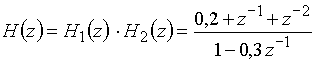 ;
;
при параллельном соединении
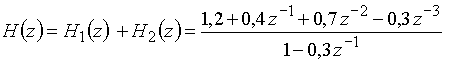 ;
;
при включении цепи ![]() в обратную связь цепи
в обратную связь цепи ![]()
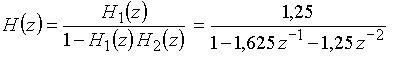 .
.
Пример 19.2. Найдем передаточную функцию дискретной цепи, изображенной на рис. 57.
Цепь, приведенная на рис. 57, представляет собой каскадное соединение типовых звеньев 1-го и 2-го порядков. Передаточная функция соединения имеет вид
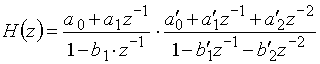 .
.
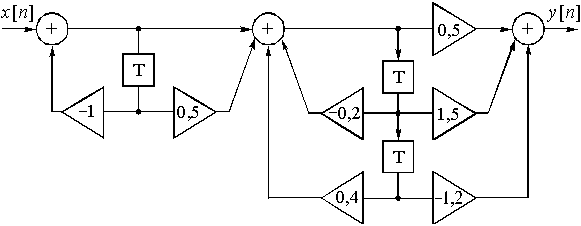
Рис. 57
Подставляя в выражение для ![]() заданные значения коэффициентов усиления
заданные значения коэффициентов усиления ![]() = 1,
= 1, ![]() = 0,5,
= 0,5, ![]() = -1 и
= -1 и ![]() = 0,5,
= 0,5, ![]() = 1,5,
= 1,5, ![]() = -1,2,
= -1,2, ![]() = -0,2,
= -0,2, ![]() = 0,4, получаем
= 0,4, получаем
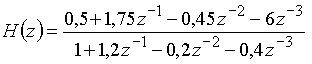 .
.
Самоконтроль
1. Как определить передаточные функции каскадного и параллельного соединений типовых звеньев?
2. Как определить передаточную функцию дискретной цепи с обратной связью?
3. Найдите передаточную функцию каскадного соединения звеньев, имеющих 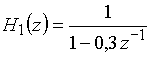 и
и 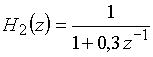 . Приведите структурную схему этого соединения.
. Приведите структурную схему этого соединения.
4. Повторите п. 3, но для параллельного соединения звеньев.
Вопрос 20. Может ли дискретная цепь осуществлять фильтрацию сигнала?
Дискретная цепь может осуществлять любые операции: фильтрацию сигнала, корректирование характеристик и т.п., т.е. выполнять функции любой аналоговой цепи.
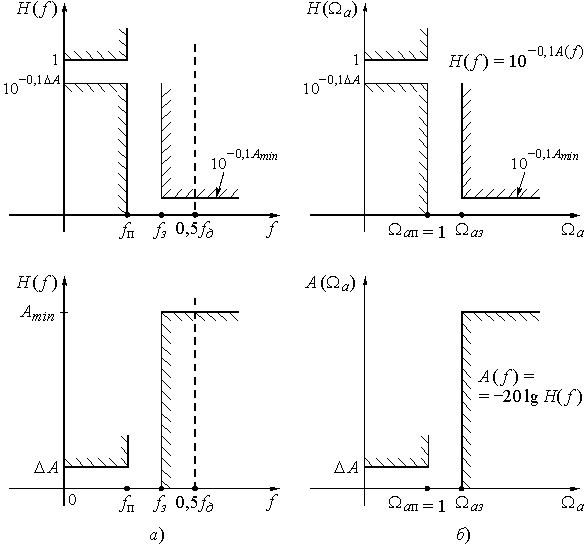
Рис. 58
В частности, при синтезе дискретных частотных фильтров нужно найти такие коэффициенты передаточной функции (19), (22) или (24), частотная характеристика которой удовлетворяла бы нормам ослабления фильтра в полосах пропускания и непропускания (рис. 58,а). Определение коэффициентов - это задача аппроксимации. Известен целый ряд методов ее решения. Наиболее распространенным является следующий метод. Сначала рассчитывают аналоговый НЧ-прототип и получают его передаточную функцию ![]() , затем путем замены комплексной переменной
, затем путем замены комплексной переменной ![]() переходят от
переходят от ![]() к передаточной функции дискретной цепи
к передаточной функции дискретной цепи ![]() .
.
Использование стандартного преобразования ![]() или
или ![]() не приведет к дробно-рациональной функции. Поэтому для ФНЧ применяют билинейное преобразование
не приведет к дробно-рациональной функции. Поэтому для ФНЧ применяют билинейное преобразование
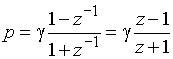 . (28)
. (28)
(g - некоторый постоянный множитель), которое является первым приближением стандартного преобразования при разложении его в ряд Тейлора:
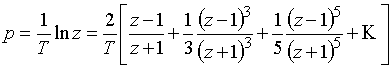 . (29)
. (29)
Из разложения (29) следует, что необходимо выбирать ![]() . Однако, далее мы покажем, что удобнее брать другие значения коэффициента g.
. Однако, далее мы покажем, что удобнее брать другие значения коэффициента g.
Билинейное преобразование (28) переводит все точки из левой полуплоскости переменной p в точки на единичной окружности плоскости z. Так что, если была устойчива аналоговая цепь, будет устойчивой и дискретная. Подтвердим эти утверждения на примере.
Пример 20.1. Найдем положения точек на z-плоскости, соответствующих следующим значениям переменной p: ![]() ;
; ![]() = -2 + j2;
= -2 + j2; ![]() = j2.
= j2.
Из формулы (28) найдем выражение для расчета z:
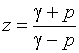 .
.
Подставляя в эту формулу значение полюса p =![]() = -2, лежащего в левой полуплоскости плоскости p, получаем
= -2, лежащего в левой полуплоскости плоскости p, получаем
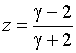 .
.
Поскольку g - число вещественное и положительное, то числитель (g - 2) меньше знаменателя (g + 2), и значит z< 1, т.е. точка z лежит внутри единичной окружности, что говорит об устойчивости цепи.
При p = ![]() = -2 + j2 получаем
= -2 + j2 получаем
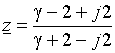 .
.
Найдем модуль z
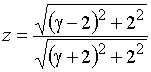 .
.
Он меньше единицы, поскольку модуль числителя меньше модуля знаменателя, т.е. точка z также лежит внутри единичной окружности.
При p =![]() = j2 получаем
= j2 получаем
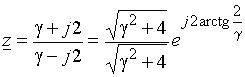 .
.
Модуль z равен 1, т.е. точка p = j2, лежащая на мнимой оси плоскости p, переходит в точку на единичной окружности плоскости z при использовании билинейного преобразования.
Переход к аналоговому прототипу применяется обычно для дискретных фильтров, имеющих бесконечную импульсную характеристику ![]() , принимающую ненулевые значения на бесконечном множестве значений n = 0, 1, ... .
, принимающую ненулевые значения на бесконечном множестве значений n = 0, 1, ... .
Дискретные цепи с конечной импульсной характеристикой, принимающей ненулевые значения лишь при n = 0, 1, ..., N - 1, не имеют аналогов среди пассивных электрических фильтров, поэтому для их расчета применяются другие методы.
Нерекурсивные фильтры с передаточной функцией (19) всегда имеют конечные импульсные характеристики. Рекурсивные фильтры с передаточными функциями (22) и (24) могут иметь как конечные, так и бесконечные импульсные характеристики.
Пример 20.2. Найдем дискретные импульсные характеристики фильтров, имеющих передаточные функции
![]() ,
, 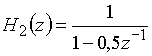 ,
,
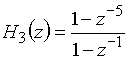 .
.
Дискретная импульсная характеристика ![]() - это обратноеz-преобразование передаточной функции
- это обратноеz-преобразование передаточной функции ![]() , т.е.
, т.е. ![]() . Нерекурсивной цепи с передаточной функцией
. Нерекурсивной цепи с передаточной функцией ![]() соответствует
соответствует ![]() = {2; 0,5; -3}, т.е. это фильтр с конечной импульсной характеристикой.
= {2; 0,5; -3}, т.е. это фильтр с конечной импульсной характеристикой.
Импульсная характеристика цепи с передаточной функцией ![]() рассчитывается по формуле
рассчитывается по формуле ![]() (см. пример 10.1), т.е. это рекурсивный фильтр с бесконечной импульсной характеристикой.
(см. пример 10.1), т.е. это рекурсивный фильтр с бесконечной импульсной характеристикой.
Отсчеты импульсной характеристики рекурсивной цепи с передаточной функцией ![]() будут конечными и равными 1 только для n = 0, 1, 2, 3, 4, а для n³ 5
будут конечными и равными 1 только для n = 0, 1, 2, 3, 4, а для n³ 5 ![]() . Значит этот рекурсивный фильтр имеет конечную импульсную характеристику.
. Значит этот рекурсивный фильтр имеет конечную импульсную характеристику.
Самоконтроль
1. В чем суть задачи аппроксимации и метода ее решения для дискретных фильтров?
2. Какое билинейное преобразование применяется при расчете дискретных фильтров?
3. Почему при использовании билинейного преобразования устойчивой аналоговой цепи соответствует устойчивая дискретная цепь?
4. Докажите, что дискретная цепь неустойчива, если полюс передаточной функции соответствующей аналоговой цепи лежит в правой полуплоскости плоскости p, т.е. p = a + jw, a> 0.
5. Что такое конечная (и бесконечная) импульсная характеристика?
6. Какая импульсная характеристика у нерекурсивных (у рекурсивных) фильтров: конечная или бесконечная?
Вопрос 21. Как пересчитать требования к дискретному (цифровому) фильтру в требования к аналоговому прототипу?
Следует иметь в виду, что частотная характеристика аналогового фильтра определена на всей положительной полуоси частот, в то время как у дискретного фильтра она имеет тот же смысл только до частоты ![]() , затем она периодически повторяется (рис. 50). Ясно, что шкала частот дискретного фильтра оказывается деформированной относительно шкалы частот аналогового фильтра. Соответствие этих шкал легко установить из билинейного преобразования (28). Перепишем его в виде:
, затем она периодически повторяется (рис. 50). Ясно, что шкала частот дискретного фильтра оказывается деформированной относительно шкалы частот аналогового фильтра. Соответствие этих шкал легко установить из билинейного преобразования (28). Перепишем его в виде:
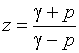 . (30)
. (30)
Обозначим, во избежание путаницы, нормированную частоту для аналогового фильтра-прототипа ![]() , обычную (т.е. ненормированную) частоту для дискретного фильтра будем, как и ранее, обозначать буквой f, а нормированную - буквой W. Теперь заменим в (30) комплексную переменную p на
, обычную (т.е. ненормированную) частоту для дискретного фильтра будем, как и ранее, обозначать буквой f, а нормированную - буквой W. Теперь заменим в (30) комплексную переменную p на ![]() , а комплексную переменную z на
, а комплексную переменную z на ![]() и установим соответствие между частотами f (или W) и
и установим соответствие между частотами f (или W) и ![]() :
:
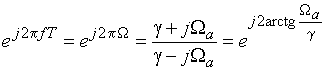 .
.
Отсюда легко получить, что
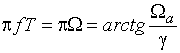
или
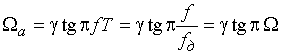 . (31)
. (31)
При изменении частоты f от 0 до ![]() , или нормированной частоты Wот 0 до 0,5, нормированная частота
, или нормированной частоты Wот 0 до 0,5, нормированная частота ![]() в шкале аналогового прототипа будет пробегать значения от 0 до бесконечности (рис. 58, б).
в шкале аналогового прототипа будет пробегать значения от 0 до бесконечности (рис. 58, б).
Во многих справочниках по расчету фильтров граничная частота полосы пропускания принимается равной ![]() . Чтобы частота
. Чтобы частота ![]() (или
(или ![]() ) дискретного фильтра пересчитывалась в
) дискретного фильтра пересчитывалась в ![]() (рис. 58, б), из (31) ясно, что коэффициент g нужно взять равным:
(рис. 58, б), из (31) ясно, что коэффициент g нужно взять равным:
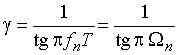 . (32)
. (32)
Пример 21.1. Рассчитаем дискретный ФНЧ с параметрами: ![]() = 8 кГц;
= 8 кГц; ![]() = 1 кГц;
= 1 кГц; ![]() = 3 кГц; DA = 1,4 дБ;
= 3 кГц; DA = 1,4 дБ; ![]() = 40 дБ.
= 40 дБ.
По формуле (32) находим ![]() и по формуле (31) определяем нормированную граничную частоту полосы непропускания
и по формуле (31) определяем нормированную граничную частоту полосы непропускания ![]() аналогового НЧ-прототипа:
аналогового НЧ-прототипа:
![]() .
.
Тем самым, произведен пересчет требований, предъявленных к дискретному фильтру (рис. 58, а) в требования к аналоговому НЧ-прототипу (рис. 58, б).
Самоконтроль
1. Как рассчитать нормированную частоту аналогового фильтра-прототипа, если известна нормированная частота дискретного фильтра?
2. Как изменяется нормированная частота аналогового фильтра-прототипа при изменении частоты дискретного фильтра от 0 до ![]() ?
?
3. Рассчитайте нормированную частоту аналогового фильтра-прототипа, соответствующую частоте 4 кГц дискретного фильтра, имеющего частоту дискретизации 20 кГц и граничную частоту полосы пропускания 2 кГц.
Вопрос 22. Как рассчитать аналоговый фильтр-прототип?
Исходными данными для расчета являются требования к НЧ-пототипу (рис. 50, б). По ним, пользуясь любым справочником, рассчитывают передаточную функцию фильтра-прототипа.
Пример 22.1 Для ![]() = 5,82,
= 5,82, ![]() = 40 дБ и DA = 1,4 дБ, (параметры ФНЧ, взятые из Примера 21.1), пользуясь справочником Христиана Э., Эйзенмана Е. «Таблицы и графики по расчету фильтров» (М.: Связь, 1975), находим, что
= 40 дБ и DA = 1,4 дБ, (параметры ФНЧ, взятые из Примера 21.1), пользуясь справочником Христиана Э., Эйзенмана Е. «Таблицы и графики по расчету фильтров» (М.: Связь, 1975), находим, что
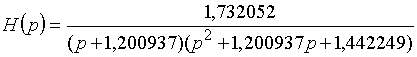 . (33)
. (33)
Вопрос 23. Как осуществить переход к дискретному фильтру?
Для перехода от аналогового фильтра к дискретному воспользуемся заменой переменных (28)
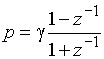 .
.
Пример 23.1. От передаточной функции (33) аналогового фильтра-прототипа перейдем к передаточной функции ![]() дискретного фильтра.
дискретного фильтра.
Подставим в выражение (33) значение
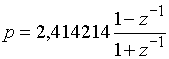 .
.
Получим
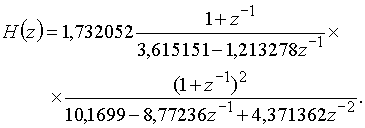
Дискретный фильтр можно реализовать в виде каскадного соединения типовых звеньев 1-го и 2-го порядка. Для этого функцию ![]() перепишем в виде:
перепишем в виде:
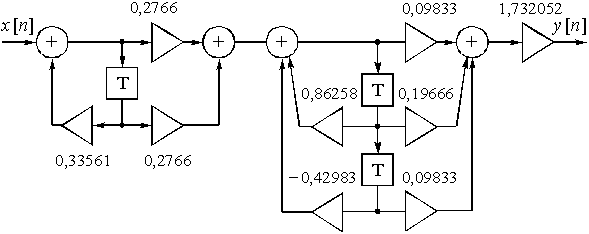
Рис. 59
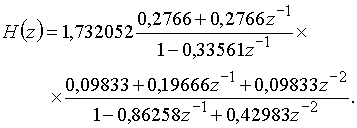
Схема фильтра, имеющего такую передаточную функцию, приведена на рис. 59. Амплитудно-частотная характеристика ![]() , рассчитанная на основании формул для АЧХ типовых звеньев, показана на рис. 60 (кривая 1).
, рассчитанная на основании формул для АЧХ типовых звеньев, показана на рис. 60 (кривая 1).
Аналогичным образом производится расчет фильтров со всплесками ослабления (нулями передачи).
Пример 23.2.Найдем передаточную функцию дискретного фильтра НЧ с АЧХ, равноволновой в полосе пропускания и со всплеском ослабления в полосе задерживания. Параметры фильтра: ![]() = 32 кГц;
= 32 кГц; ![]() = 6 кГц;
= 6 кГц; ![]() = 8,8 кГц; DA = 1,5 дБ;
= 8,8 кГц; DA = 1,5 дБ;![]() = 30 дБ.
= 30 дБ.
Определяем: ![]() и
и
![]() . Далее находим
. Далее находим
![]() и
и
![]() .
.
По справочнику рассчитываем
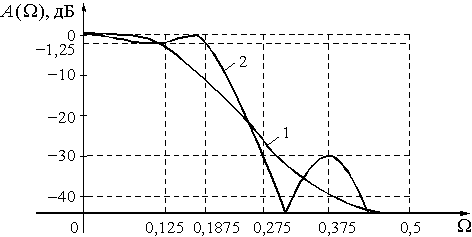
Рис. 60
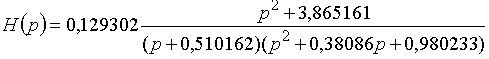
и с помощью подстановки
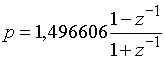
переходим к ![]()
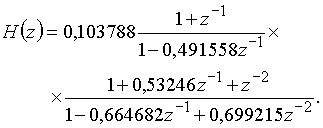
Амплитудно-частотная характеристика ![]() такого фильтра показана на рис. 60 (кривая 2).
такого фильтра показана на рис. 60 (кривая 2).
Самоконтроль
1. Как осуществить переход от передаточной функции аналогового фильтра к передаточной функции дискретного фильтра?
2. Как составить структурную схему дискретного фильтра, реализующего полученную передаточную функцию?
3. Как построить график АЧХ дискретного фильтра с рассчитанной передаточной функцией?
Вопрос 24. Как реализовать фильтр с конечной импульсной характеристикой?
Если известна передаточная функция ![]() дискретного фильтра, то для реализации фильтра с конечной импульсной характеристикой
дискретного фильтра, то для реализации фильтра с конечной импульсной характеристикой ![]() , равной нулю везде кроме
, равной нулю везде кроме ![]() , поступают следующим образом. Амплитудно-частотную характеристику
, поступают следующим образом. Амплитудно-частотную характеристику ![]() фильтра дискретизируют, разбивая частотный интервал W = 0 ¸ 1 на N равных интервалов. В результате получают последовательность отсчетов АЧХ на N частотах
фильтра дискретизируют, разбивая частотный интервал W = 0 ¸ 1 на N равных интервалов. В результате получают последовательность отсчетов АЧХ на N частотах ![]() , т.е.
, т.е. ![]() ,
, ![]() . Поскольку
. Поскольку ![]() , то, подставляя эту последовательность в формулу обратного дискретного преобразования Фурье (10), получаем выражение для дискретной импульсной характеристики
, то, подставляя эту последовательность в формулу обратного дискретного преобразования Фурье (10), получаем выражение для дискретной импульсной характеристики ![]() фильтра
фильтра
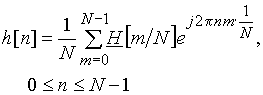 (34)
(34)
Как известно, конечную импульсную характеристику имеют нерекурсивные фильтры. Это значит, что полученные отсчеты дискретной импульсной характеристики ![]() являются коэффициентами усиления
являются коэффициентами усиления ![]() ,
, ![]() , ...,
, ..., ![]() в схеме нерекурсивного фильтра, приведенной на рис. 40, а.
в схеме нерекурсивного фильтра, приведенной на рис. 40, а.
Пример 24.1. Найдем импульсную характеристику ![]() фильтра нижних частот, имеющего граничную частоту полосы пропускания W = 0,1, и АЧХ, приведенную на рис. 61. Импульсную характеристику будем рассчитывать для значения N = 30.
фильтра нижних частот, имеющего граничную частоту полосы пропускания W = 0,1, и АЧХ, приведенную на рис. 61. Импульсную характеристику будем рассчитывать для значения N = 30.
В формуле (34) для расчета ![]() используются комплексные значения передаточной функции. Если выбрать значения
используются комплексные значения передаточной функции. Если выбрать значения ![]() , показанные на рис. 61 (
, показанные на рис. 61 (![]() = 1 в полосе пропускания и
= 1 в полосе пропускания и ![]() = 0 в полосе непропускания) и фазу передаточной функции
= 0 в полосе непропускания) и фазу передаточной функции ![]() , равную нулю, то передаточная функция будет иметь заданные значения в точках
, равную нулю, то передаточная функция будет иметь заданные значения в точках ![]() , но очень сильно отличаться от требуемой формы на частотах W между этими точками.
, но очень сильно отличаться от требуемой формы на частотах W между этими точками.
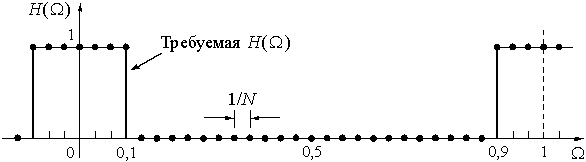
Рис. 61
Гораздо лучшие результаты получаются, если выбрать ![]() . Выбор такой фазы эквивалентен тому, что
. Выбор такой фазы эквивалентен тому, что ![]() вместо 1 в полосе пропускания. Такой передаточной функции соответствует АЧХ, изображенная на рис. 62. Подстановка значений
вместо 1 в полосе пропускания. Такой передаточной функции соответствует АЧХ, изображенная на рис. 62. Подстановка значений ![]() в формулу (34) позволяет получить выражение для расчета
в формулу (34) позволяет получить выражение для расчета ![]() :
:
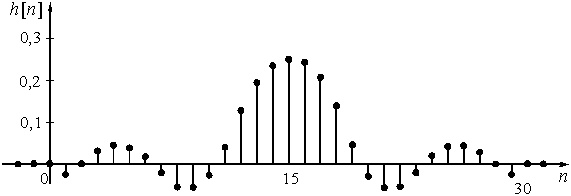
Рис. 63
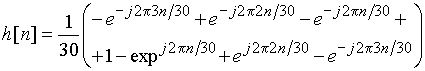 .
.
График конечной импульсной характеристики ![]() изображен на рис. 63.
изображен на рис. 63.
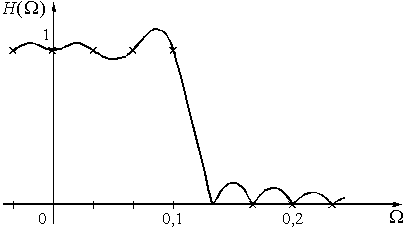
Рис. 62
Для реализации фильтра с такой импульсной характеристикой по схеме рис. 40, а потребуется 30 усилителей и 29 элементов задержки, т.е. схема довольно громоздкая. Схема с обратными связями, реализующая АЧХ, изображенную на рис. 61, будет иметь гораздо меньше элементов. Однако достоинством нерекурсивных фильтров с конечной импульсной характеристикой является то, что они всегда устойчивы и, кроме того, обеспечивают линейные фазовые характеристики.
Самоконтроль
1. Каков алгоритм реализации фильтра с конечной импульсной характеристикой?
2. Как перейти от передаточной функции к дискретной импульсной характеристике фильтра?
3. Какой вид имеет структурная схема фильтра с конечной импульсной характеристикой?
Вопрос 25. Как рассчитываются дискретные фильтры верхних частот, полосовые и режекторные?
Требования к любому типу фильтра преобразуются в требования к аналоговому ФНЧ-прототипу. Затем рассчитывается аналоговый прототип, как это показано выше, и с помощью замены переменных переходят от ![]() к
к ![]() .
.
Конечно, формулы замены переменных уже не такие, как для ФНЧ. Они приведены для разных типов фильтров в табл. 2. Требования к дискретным фильтрам графически изображены на рис. 64.
Пример 25.1. Определить передаточную функцию дискретного полосового фильтра с параметрами: ![]() = 140 Гц;
= 140 Гц; ![]() = = 15,5 Гц;
= = 15,5 Гц; ![]() = 30 Гц;
= 30 Гц; ![]() = 7,75 Гц;
= 7,75 Гц; ![]() = 60 Гц;
= 60 Гц; ![]() = 0,5 дБ;
= 0,5 дБ; ![]() = 40 дБ.
= 40 дБ.
Определяем:
![]() = 15,5/140 = 0,110714;
= 15,5/140 = 0,110714; ![]() = 30/140 = 0,214286;
= 30/140 = 0,214286;
![]() = 7,75/140 = 0,055357;
= 7,75/140 = 0,055357; ![]() = 60/140 = 0,428571;
= 60/140 = 0,428571;
![]() = 2,964087;
= 2,964087;
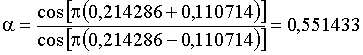 ;
;
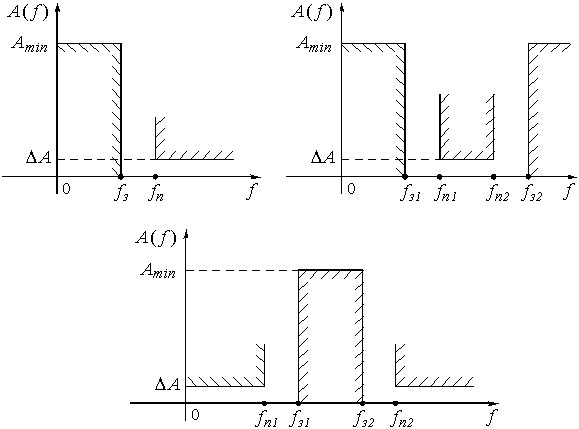
Рис. 64
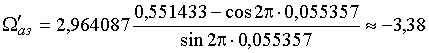 ;
;
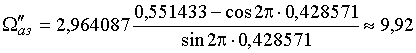 ;
;
![]() .
.
По данным ![]() = 3,38, DА = 0,5 дБ и
= 3,38, DА = 0,5 дБ и ![]() =40 дБ из справочника находим
=40 дБ из справочника находим
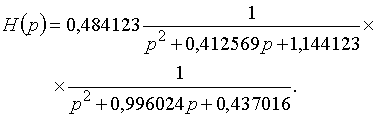
Передаточную функцию ![]() найдем, используя подстановку
найдем, используя подстановку
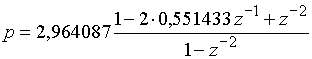
и разлагая каждый из двух полиномов четвертой степени (в знаменателе ![]() ) на множители (полиномы второй степени):
) на множители (полиномы второй степени):
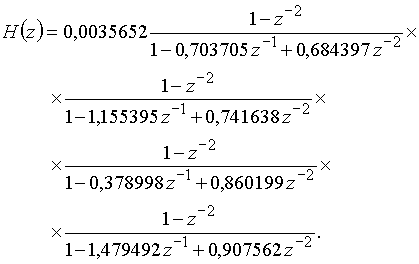
Самоконтроль
1. Каков порядок расчета дискретного фильтра верхних частот (полосового, режекторного)?
2. Какие формулы замены переменных (p и z) используются при расчете дискретного фильтра верхних частот (полосового, режекторного)?
3. Как рассчитать нормированную частоту аналогового дискретного фильтра верхних частот (полосового, режекторного), если известна соответствующая частота дискретного фильтра?
Вопрос 26. В чем состоят особенности расчета цифровых фильтров?
В цифровом фильтре хранение и обработка чисел (представленных, как мы уже знаем, в двоичном коде) осуществляется в устройствах (элементах памяти, умножителях, сумматорах) с конечным числом разрядов. Поэтому расчет цифрового фильтра, помимо определения передаточной функции ![]() фильтра и его структурной схемы (см. в предыдущих вопросах) включает в себя также расчет разрядностей АЦП и ЦАП (см. рис. 8) и разрядностей резисторов оперативной памяти (умножителей, сумматоров).
фильтра и его структурной схемы (см. в предыдущих вопросах) включает в себя также расчет разрядностей АЦП и ЦАП (см. рис. 8) и разрядностей резисторов оперативной памяти (умножителей, сумматоров).
Кроме того, при расчете цифрового фильтра предусматривают расчет масштабных множителей, вводимых в схему для предотвращения переполнения регистров фильтра, а также проверку устойчивости фильтра. Более подробно с расчетом цифровых фильтров можно ознакомиться в книге «Цифровые фильтры в электросвязи и радиотехнике» (под ред. Л.М. Гольденберга, М.: Радио и связь, 1982).
Ответы:
1.= {0,5; 1; 1; 0,5}
2. а)
= {1; 1,5; 0,75; 0,25} б)
= {2; 4; 6; 4; 2}
3. а)
б)
в)
4.
5. а)
= {1; 2; 0; 4} б)
6.
= {1; 0; 0; 0}
7.
= {1,875; 0,838; 0,625; 0,838}
= {0; –0,464; 0,0464}
8. а)
= {1; 1; 1; 1} б)
= {1; 1; 1; 1},
9. а)
б)
в)
10. а)
,
= {1; –0,5; 2} б)
,
= {1; 0,5; –0,75; –0,875; ...} в)
,
= {2; 0,5; 1,75; –0,625; ...}
11. а)
= {1; 0,5; 2,5} б)
= {1; 1,5; 0,75} в)
= {2; 2,5; 4,25}
12. а)
= {0,5; –2; 1} б)
= {1; –3; 11;–39; ...} в)
= {1; –2,5; 6;–14,5; ...}
13. а)
б)
в)
14. а)
,
= {5; –1; 3} б)
,
= {2; 4; 8; 16; ...} в)
,
= {5; 1; 11; 13; ...}
15. а) устойчивая б) неустойчивая в) неустойчивая
16.
17. а)
= 1, n³0 б)
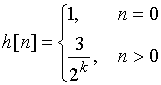
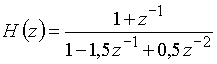
18. а)
б)
19.
= {1; 1,5; 1,5; 0,5}
20. а)
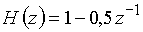
б)
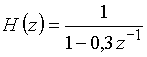
Задачи для самостоятельного решения
1. Найти дискретную свертку сигналов ![]() = {1; 1} и
= {1; 1} и ![]() = = {0,5; 0,5; 0,5}
= = {0,5; 0,5; 0,5}
2. Вычислить реакцию дискретной цепи с импульсной характеристикой ![]() на входной дискретный сигнал
на входной дискретный сигнал ![]() :
:
а) ![]() = {2; 1; 0,5},
= {2; 1; 0,5}, ![]() = {0,5; 0,5}
= {0,5; 0,5}
б) ![]() = {2; 2; 2},
= {2; 2; 2}, ![]() = {1; 1; 1}
= {1; 1; 1}
3. Найти z-преобразование дискретных сигналов
а) ![]() = {3; 2; 1}
= {3; 2; 1}
б) 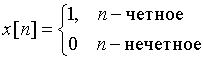
в) 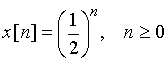
4. Найти z-преобразование дискретного сигнала ![]() , равного сумме сигналов
, равного сумме сигналов ![]() = {1; 0; 1; -1} и
= {1; 0; 1; -1} и ![]() = {2; 1; 0; 1}
= {2; 1; 0; 1}
5. Найти дискретные сигналы ![]() , имеющие z-преобразования
, имеющие z-преобразования
а) ![]()
б) ![]()
6. Найти дискретное преобразование Фурье прямоугольного импульса, заданного четырьмя единичными отсчетами.
7. Найти ДПФ дискретного сигнала ![]() = {0,5; 0,25; 0,0625}. Построить спектр амплитуд и спектр фаз дискретного сигнала.
= {0,5; 0,25; 0,0625}. Построить спектр амплитуд и спектр фаз дискретного сигнала.
8. Найти отсчеты дискретных сигналов ![]() , имеющих спектры
, имеющих спектры
а) ![]() {4; 0; 0; 0}
{4; 0; 0; 0}
б) ![]() {0; 4; 0; 0}
{0; 4; 0; 0}
9. Записать разностные уравнения для дискретных цепей, структурные схемы которых приведены на рис. 65.
10. Записать передаточные функции цепей, приведенных на рис. 65, и определить их импульсные характеристики.
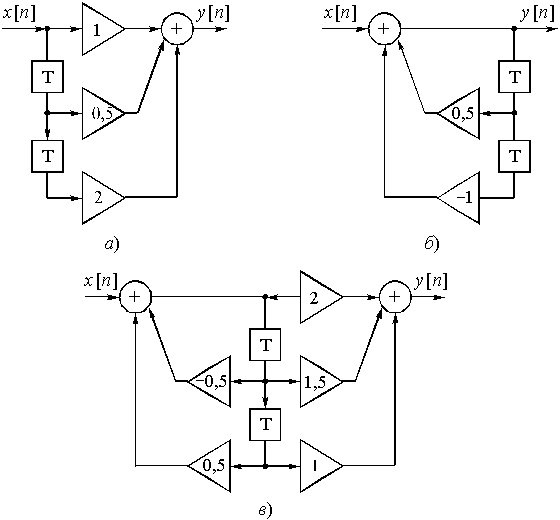
Рис. 65
11. Рассчитать отсчеты ![]() ,
, ![]() и
и ![]() выходных сигналов цепей, приведенных на рис. 65, если входной сигнал - ступенчатая последовательность
выходных сигналов цепей, приведенных на рис. 65, если входной сигнал - ступенчатая последовательность ![]() =
= ![]() = {1; 1; 1; 1; ...}
= {1; 1; 1; 1; ...}
12. Определить импульсные характеристики цепей, описываемых разностными уравнениями:
а) ![]()
б) ![]()
в) ![]()
13. Определить передаточные функции цепей, описываемых разностными уравнениями, приведенными в задаче 12.
14. Составить структурные схемы, записать разностные уравнения и определить импульсные характеристики цепей, передаточные функции которых имеют вид
а) ![]()
б) 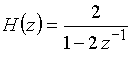
в) 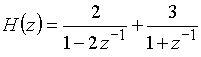
15. Определить устойчивость цепей, имеющих передаточные функции, приведенные в задаче 14.
16. Определить передаточную функцию цепи, если на ее входе и выходе действуют дискретные сигналы ![]() = {1; 0; 0; 0; 1; 0; 0; 0; 1; ...},
= {1; 0; 0; 0; 1; 0; 0; 0; 1; ...}, ![]() = {1; 0; 1; 0; 1; 0; ...}
= {1; 0; 1; 0; 1; 0; ...}
17. Найти импульсные характеристики дискретных цепей, имеющих передаточные функции
а) 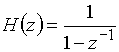
б) 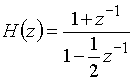
Составить структурную схему каскадного соединения этих цепей, определить для нее передаточную функцию и записать разностное уравнение
18. Найти передаточную функцию дискретной цепи с импульсной характеристикой
а) ![]() = {1; -1}
= {1; -1}
б) ![]()
19. Определить сигнал на выходе дискретной цепи с импульсной характеристикой ![]() = {1; 0,5}, если на вход подается сигнал
= {1; 0,5}, если на вход подается сигнал ![]() = {1; 1; 1}
= {1; 1; 1}
20. Определить передаточные функции и АЧХ дискретных цепей, имеющих разностные уравнения:
а) ![]()
б) ![]()
Список литературы
1. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. – М.: Радио и связь, 1998.
2. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 1988.
3. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1986.
4. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. Справочник – М.: Радио и связь, 1985.
5. Цифровые фильтры в электросвязи и радиотехнике /Под ред. Л.М. Гольденберга. – М.: Радио и связь, 1982.
6. Сиберт У.М. Цепи, сигналы, системы: в 2-х ч.: Пер. с англ. – М.: Мир, 1988.
7. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. – М.: Высшая школа, 1987.
8. Жуков В.П., Карташев В.Г., Николаев А.М. Задачник по курсу «Радиотехнические цепи и сигналы»: Учеб. пособие для студентов вузов спец. «Радиотехника» – М.: Высшая школа, 1986.
9. Воробиенко П.П., Нечипорук О.Л. Дискретные цепи (системы) и сигналы. Учебное пособие. – Одесса.: ОЭИС, 1990.