В качестве энергии Wx дискретного сигнала x(nT) применяется мера:
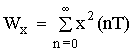
Энергию можно вычислить и в частотной области, применяя равенство Парсеваля:
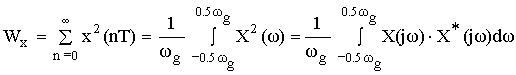
– спектр сигнала x(nT).
– спектр инверсного сигнала x(-nT).
X(jω) · X*(jω) = X2(ω) = Sx(jω) – энергетический спектр сигнала x(nT).
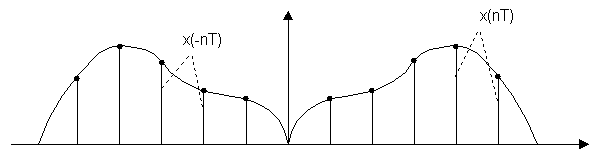
Энергетическому спектру Sx(jω) соответствует во временной области корреляционная функция Sx(nT) сигнала x(nT).
В соответствии с определением энергетического спектра корреляционная функция определяется сверткой сигнала с инверсной копией.
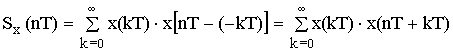– формула корреляции сигнала x(nT).
Согласно формуле корреляции в точке:
n = 0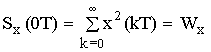 
Если Sx(jω) – спектр непрерывного сигнала Sx(nT), то Sx(jmω1) – спектр периодической дискретной последовательности Sx(nT).
Периодическая дискретная последовательность Sx(nT) определяется через свой спектр по формуле обратного ДПФ.
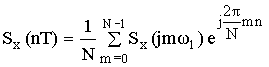
При n = 0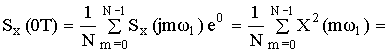 
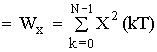– равенство Парсеваля для периодической дискретной последовательности.