9.7. Определение, разработка и оценка систем цифровой связи

Категория: 9. Компромиссы при использовании модуляции и кодирования

9.7.1. М-арная передача сигналов

9.7.2. Системы ограниченной полосы пропускания

9.7.3. Системы ограниченной мощности

9.7.4. Требования к передаче сигналов MPSK и MFSK

9.7.5. Система ограниченной полосы пропускания без кодирования

9.7.6. Система ограниченной мощности без кодирования

9.7.7. Система ограниченной мощности и полосы пропускания с кодированием

9.7.7.1. Расчет эффективности кодирования

9.7.7.2. Выбор кода

Этот раздел призван помочь в описании характерных этапов, которые следует рассматривать при удовлетворении требований, касающихся мощности, полосы пропускания и достоверности передачи в системе цифровой связи. Далее приводится несколько примеров систем, в которых подробно описываются критерии выбора схем кодирования и модуляции, исходя из типа системы — является ли она системой ограниченной мощности или системой ограниченной полосы пропускания. Подчеркиваются тонкие, но важные моменты преобразования битов данных в канальные биты, затем в символы и далее в элементарные сигналы.

Разработка любой системы цифровой связи начинается с описания канала (принимаемая мощность, доступная полоса пропускания, статистики шума и иных ухудшений качества сигнала, таких, например, как замирание) и определения системных требований (скорость передачи данных и вероятность появления ошибок). После описания канала нужно определиться с проектными решениями, которые позволят наилучшим образом использовать канал и удовлетворить требования производительности. Описание производительности системы включает в себя традиционный набор преобразований и расчетов. После того как такой подход станет понятным, его можно использовать как образец для оценки большинства систем связи. В последующих разделах будут рассмотрены три примера систем: система ограниченной мощности без кодирования, система ограниченной полосы без кодирования и система ограниченной мощности и полосы с кодированием. В данном разделе представлены системы связи реального времени, в которых термин кодированный (или некодированный) означает наличие (или отсутствие) кода коррекции ошибок, включающего использование избыточных битов и увеличение ширины полосы пропускания.

Два основных ресурса связи — это переданная мощность и ширина полосы пропускания. В различных системах связи один из этих ресурсов дороже другого, и следовательно, большую часть систем можно классифицировать как системы ограниченной мощности или ограниченной полосы пропускания. В системах ограниченной мощности для экономии энергии за счет полосы пропускания можно применять схемы кодирования, эффективно использующие мощность, тогда как в системах ограниченной полосы можно использовать методы эффективной (с точки зрения используемого спектра) модуляции для экономии полосы частот за счет увеличения расхода энергии. В обоих случаях для экономии энергии или повышения достоверности передачи при расширении полосы пропускания можно применять кодирование с коррекцией ошибок (часто называемое канальным кодированием). Для повышения надежности передачи в каналах с ограниченной полосой пропускания без увеличения ширины полосы пропускания часто используется решетчатое кодирование (trellis-coded modulation — ТСМ) [6]. Эти методы рассматриваются в разделе 9.10.

9.7.1. М-арная передача сигналов

При использовании схемы, в которой за такт обрабатывается k бит, передача сигналов называется М-арной (см. раздел 3.8). Каждый символ М-арного алфавита можно однозначно связать с последовательностью из k бит, где

(9.13)

и М — размер алфавита. Если передача является цифровой, термин символ означает элемент M-арного алфавита, передаваемый за время символьного интервала TS. Для передачи символ следует представить в виде сигнала напряжения или тока. Поскольку сигнал представляет символ, термины символ и сигнал иногда используются как синонимы. Поскольку один из М символов (или сигналов) передается за интервал TS, скорость передачи данных R можно записать в следующем виде.

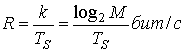(9.14)

Из соотношения (9.14) эффективную длительность Tb каждого бита можно представить через длительность символа TS или скорость передачи данных RS.

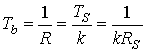(9.15)

Далее на основе выражений (9.13) и (9.15) через скорость передачи битов R можно записать скорость передачи символов RS.

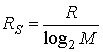(9.16)

Из соотношений (9.14) и (9.15) видно, что в любой цифровой схеме передачи k=(log2 М) бит за TS секунд, при ширине полосы пропускания в W Гц, эффективность использования полосы частот записывается следующим образом.

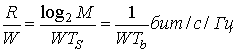(9.17)

В данном случае Tb — это эффективное время передачи каждого бита.

9.7.2. Системы ограниченной полосы пропускания

Из уравнения (9.17) видно, что в любой системе цифровой связи эффективность использования полосы частот возрастает при увеличении произведения WTb. Следовательно, в системах ограниченной полосы пропускания часто применяются сигналы с малыми значениями произведения WTb. Например, в системе GSM (Global System for Mobile — глобальная система мобильной связи) используется гауссова манипуляция с минимальным сдвигом (Gaussian minimum shift keying — OMSK), в которой произведение WTb равно 0,3 Гц/бит/с [7], где W— ширина полосы частот по уровню 3 дБ.

При использовании системы ограниченной полосы пропускания без кодирования задачей является получение максимально возможного объема переданной информации в заданной полосе пропускания за счет Eb|N0 (сохраняя при этом определенное значение Pb). На графике эффективности использования полосы частот (рис. 9.6) показаны рабочие точки когерентной M-арной схемы PSK (MPSK) при Pb=10-5. Предполагается, что немодулированный сигнал подвергается фильтрации по Найквисту (идеальной прямоугольной) [2], так что для модуляции MPSK минимальная двойная полоса пропускания, центрированная на промежуточной частоте (intermediate frequency — IF), связана со скоростью передачи символов.

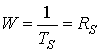(9.18).

Здесь TS — время передачи символа, a RS — скорость передачи символов. Фильтрация по Найквисту дает минимальную полосу пропускания, при которой существует нулевая межсимвольная интерференция; такая идеальная фильтрация определяет минимальную ширину полосы по Найквисту. Следует отметить, что при неортогональной передаче сигналов (например, MPSK или MQAM) полоса пропускания зависит не от плотности точек сигналов в группе, а только от скорости передачи сигналов. При передаче вектора сигнала система не различает, пришел ли этот сигнал из разреженного или уплотненного алфавита. Это и является свойством неортогональных сигналов, которое позволяет уплотнить пространство сигналов и, таким образом, повысить эффективность использования полосы частот за счет мощности передатчика. Из уравнений (9.17) и (9.18) запишем, насколько сигнал в модуляции MPSK эффективно использует полосу при фильтрации по Найквисту.

(9.19)

Точки MPSK, показанные на рис. 9.6, подтверждают соотношение (9.19). Отметим, что модуляция MPSK является схемой эффективного использования полосы. С увеличением М также растет RIW. Из рис. 9.6 можно убедиться, что модуляция MPSK действительно может дать повышение эффективности использования полосы частот за счет увеличения Eb|N0. Было найдено множество схем модуляции, позволяющих весьма эффективно использовать полосу частот [8], но их рассмотрение выходит за рамки данной книги.

На графике эффективности использования полосы частот (рис. 9.6) показаны две области — область ограниченной полосы пропускания и область ограниченной мощности. Отметим, что желаемые компромиссы, связанные с каждой из этих областей, не являются беспристрастными. В области ограниченной полосы желательным является большое значение R/W; в тоже время с ростом Eb|N0 выравнивается кривая предельной пропускной способности и для повышения R/W требуется дополнительное увеличение EblN0. Аналогичная связь имеется в области ограниченной мощности. Здесь желательно малое отношение Eb|N0, но кривая предельной пропускной способности становится более крутой и для незначительного снижения требуемого Eb|N0 нужно уменьшить R/W.

9.7.3. Системы ограниченной мощности

Для систем ограниченной мощности, где имеется достаточная полоса пропускания, но существует дефицит мощности (например, линия космической связи), возможны следующие компромиссы (см. рис. 9.1, а): 1) уменьшение Рвза счет полосы пропускания при фиксированном Eb|N0; 2) снижение Eb|N0 за счет полосы пропускания при фиксированном Рв. "Естественным" вариантом при выборе модуляции для систем ограниченной мощности представляется М-арная FSK (MFSK). На рис. 9.6 показаны рабочие точки для некогерентной ортогональной модуляции MFSK при Рв=10-5. Для MFSK минимальная полоса частот по Найквисту определяется следующим выражением (см. раздел 4.5.4.1):

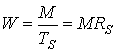(9.20)

где TS — длительность передачи символа, a RS — скорость передачи символов. При использовании MFSK необходимая полоса пропускания расширяется в М раз по сравнению с двоичной FSK, поскольку теперь существует М различных ортогональных сигналов, каждый из которых требует полосы шириной 1/ТS. Таким образом, из уравнений (9.17) и (9.20) эффективность использования полосы частот при некогерентной модуляции MFSK с фильтрацией по Найквисту можно выразить следующим образом.

(9.21)

Следует отметить важное различие между эффективностью использования полосы (R/W) схемой MPSK в уравнении (9.19) и схемой MFSK, представленной в уравнении (9.21). При MPSK R/W растет с увеличением размерности пространства сигналов М. При использовании MFSK работает два механизма. Числитель дроби R/W дает такой же эффект с увеличением M, как и в случае MPSK. Знаменатель же приводит к уменьшению значения R/W при росте М. Поскольку при увеличении М знаменатель растет быстрее числителя, это приводит к снижению R/W. Рабочие точки MFSK, показанные на рис. 9.6, подтверждают соотношение (9.21) — ортогональная передача сигналов (например, MFSK) является схемой с расширением полосы пропускания. Из рис. 9.6 видно, что модуляция MFSK вполне подходит для снижения требуемого значения Eb|N0 за счет увеличения полосы пропускания.

Здесь важно подчеркнуть, что в уравнениях (9.18) и (9.19) для MPSK, а также в уравнениях (9.20) и (9.21) для MFSK и всех рабочих точек, показанных на рис.9.6, предполагается фильтрация по Найквисту (идеальная прямоугольная). На практике такие фильтры нереализуемы. Для реальных каналов и сигналов требуемая полоса пропускания должна быть больше, чтобы учитывать реализуемость фильтров.

Во всех последующих примерах будут рассматриваться радиоканалы с аддитивным белым гауссовым шумом (additive white Gaussian noise — AWGN), не имеющие иных факторов ухудшения качества сигнала. Для простоты выбор типа модуляции будет ограничен схемами с постоянной огибающей — MPSK или некогерентная ортогональная MFSK. Таким образом, если в системах без кодирования ограничена пропускная способность канала, выбирается схема MPSK, а если у канала ограничена мощность, применяется MFSK. Отметим, что при рассмотрении кодирования с коррекцией ошибок выбор типа модуляции не так прост, поскольку существуют методы кодирования [9], которые позволяют более эффективно выбрать компромисс между полосой пропускания и мощностью, чем схемы M-арной модуляции.

Следует сказать, что в общем случае M-арную передачу сигналов можно рассматривать как процедуру кодирования формы сигнала. Иными словами, если вместо двоичной выбрана M-арная модуляция, по сути, сигналы двоичной формы заменяются сигналами лучшей формы — лучшей или с точки зрения эффективности использования полосы (MPSK), или с точки зрения требуемой мощности (MFSK). Хотя передачу ортогональных сигналов MFSK можно рассматривать как систему с кодированием (ее можно представить как код Рида-Мюллера [10]), мы будем применять термин система с кодированием только к традиционным кодам коррекции ошибок, использующим избыточность, таким как блочные или сверточные коды.

9.7.4. Требования к передаче сигналов MPSK и MFSK

Основное соотношение между скоростью передачи символов (или сигналов) RS и скоростью передачи битов R выражено в уравнении (9.16) и имеет следующий вид.

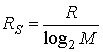
На основе этого соотношения и уравнений (9.18)—(9.21) для скорости передачи данных R=9600 бит/с была составлена табл. 9.1 [11]. В этой таблице сведены данные о скорости передачи символов, минимальной полосе пропускания по Найквисту, эффективности использования полосы частот для MPSK и некогерентной ортогональной MFSK при М = 2, 4, 8, 16 и 32. В табл. 9.1 также для каждого М показаны значения Eb|N0, необходимые для получения вероятности ошибки 10-5 для MPSK и MFSK. Эти значения Eb|N0 в таблице были получены исходя из соотношений, которые будут представлены далее, и соответствуют компромиссам, показанным на рис. 9.6. С ростом М передача сигналов MPSK позволяет более эффективно использовать полосу частот за счет увеличения Eb|N0, в то время как передача сигналов MFSK позволяет снизить Eb|N0 за счет расширения полосы пропускания. В следующих трех разделах будут подробно рассмотрены примеры из табл. 9.1.

Таблица 9.1. Скорость передачи символов, минимальная полоса по Найквисту, эффективность использования полосы и требуемое Eb|N0 для схем MPSK и некогерентной ортогональной MFSK при скорости передачи данных 9600 бит/с

M

k

R

(бит/с)

RS

(символ/с)

MPSK

Минимальная полоса (Гц)

MPSK

R/W

MPSK

Eb|N0

(дБ)

PS=10-5

Некогерентная ортогональная MFSK

Минимальная полоса (Гц)

MFSK

R/W

MFSK

Eb|N0 (дБ)

PS=10-5

2

1

9600

9600

9600

1

9,6

19200

1/2

13,4

4

2

 9600

4800

4800

2

9,6

19200

1/2

10,6

8

3

 9600

3200

3200

3

13,0

25600

1/3

9,1

16

4

 9600

2400

2400

4

17,5

38400

1/4

8,1

32

5

 9600

1920

1920

5

22,4

61440

5/32

7,4

9.7.5. Система ограниченной полосы пропускания без кодирования

Рассмотрим радиоканал с шумом AWGN и ограниченной полосой пропускания W=4000Гц. Пусть ограничения линии связи (мощность передатчика, коэффициент усиления антенны, потери в канале и т. д.) приводят к тому, что отношение мощности принятого сигнала к спектральной плотности мощности шума (Pr|N0) равно 53 дБГц. Допустим, требуемое значение скорости передачи информации R равно 9600 бит/с, а требуемая вероятность появления битовой ошибки РВ не должна превышать 10-5. Задача — выбрать схему модуляции, которая сможет удовлетворить требуемым рабочим характеристикам. В общем случае может потребоваться схема кодирования с коррекцией ошибок, если ни одна из доступных схем модуляции не может удовлетворить всем требованиям. Тем не менее в данном примере (как показывается далее) кодирование с коррекцией ошибок не понадобится.

Для любой цифровой системы связи соотношение между принимаемой мощностью и спектральной плотностью мощности шума (Pr|N0), а также принимаемой энергией одного бита и спектральной плотностью мощности шума (Eb|N0) приведено в формуле (5.20,в) и имеет следующий вид.

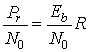(9.22)

Выразив из этого соотношения Eb|N0 в децибелах, получаем следующее.

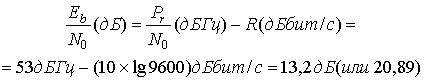(9.23)

Поскольку необходимая скорость передачи данных 9600 бит/с значительно больше, чем можно достичь с доступной полосой пропускания, составляющей 4000 Гц, канал можно считать каналом ограниченной полосы пропускания. Следовательно, в качестве схемы модуляции выбираем MPSK. Напомним, что при выборе возможной схемы модуляции было решено ограничиться модуляциями с постоянной огибающей; без такого ограничения можно найти тип модуляции с еще большей эффективностью использования полосы частот. Вычислим далее минимально допустимое значение М, при котором символьная скорость передачи данных не превышает доступной полосы пропускания 4000 Гц. Из табл. 9.1 видно, что наименьшим значением М, удовлетворяющим этим требованиям, является М=8. Следующая задача — выяснить, удовлетворяется ли требование к вероятности появления битовой ошибки PB<10-5 при использовании 8-уровневой PSK или потребуется дополнительно вводить схему кодирования с коррекцией ошибок. Из табл. 9.1 видно, что 8-уровневая PSK удовлетворяет всем требованиям, поскольку отношение Eb|N0 для 8-уровневой PSK меньше принятого Eb|N0, выраженного в (9.23). Тем ле менее, представим, что табл. 9.1 нет. Покажем, как определить, нужно ли кодирование с коррекцией ошибок.

На рис. 9.8 показана блочная диаграмма простого модулятора/демодулятора (модема), в которой отображены функциональные элементы разработки. В модуляторе в ходе преобразования битов данных в символы выходная скорость передачи символов равна RS, т.е. в (log2 М) раз меньше входной скорости передачи битов R, как видно из уравнения (9.16). Аналогично на входе демодулятора отношение энергии символа к спектральной плотности мощности шума ES|N0 в (log2 M) больше Eb|N0, поскольку каждый символ состоит из (log2 M) бит. Поскольку ES|N0 больше Eb|N0 в столько же раз, во сколько RS меньше R, формулу (9.22) можно переписать следующим образом.

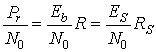(9.24)

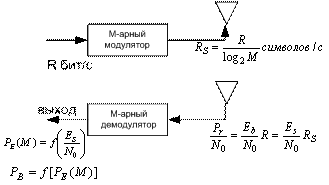
Рис.9.8. Схема простого модулятора/демодулятора (модема) без канального кодирования

За каждый интервал TS демодулятор принимает сигнал (в данном случае — один из М=8 возможных сдвигов фаз). Вероятность РE(М) возникновения в демодуляторе символьной ошибки довольно точно описывается следующим приближенным выражением [12].

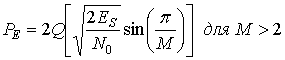(9.25)

Здесь Q(x) — это гауссов интеграл ошибок, который был определен в выражении (3.43).

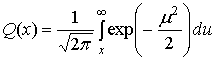
На рис. 9.8 и на всех последующих рисунках для обозначения некоторой функциональной зависимости вероятности от х будет использоваться не явное выражение, а обобщенная запись f(x).

Как правило, для описания эффективности связи (по фактору мощности) или достоверности передачи в цифровых системах их выражают через Eb|N0 в децибелах. Такое употребление Eb|N0 является распространенной практикой. Тем не менее напомним, что на входе демодулятора/детектора нет битов, имеются только сигналы, которым присвоено битовое значение. Следовательно, принимаемое значение Eb|N0 представляет собой пропорциональное распределение энергии принимаемых битов по сигналам. Более точное (но громоздкое) название — энергия эффективного бита на N0 - Для выражения РE(М) из уравнения (9.25) сначала нужно получить выражение для отношения энергии символа к спектральной плотности мощности шума, Eb|N0. Поскольку (из выражения (9.23)) Eb|N0=13,2 дБ (или 20,89) и каждый символ образуется (log2 M) битами, при М=8 получаем следующее.

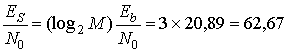(9.26)

Подставляя выражение (9.26) в (9.25), получаем вероятность появления символьной ошибки РЕ=2,210-5. Чтобы этот результат перевести в вероятность появления битовой ошибки, нужно воспользоваться соотношением между вероятностью появления битовой ошибки РВи вероятностью появления символьной ошибки РЕдля многофазной передачи сигналов [10]. Итак,

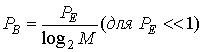(9.27)

Это является довольно хорошей аппроксимацией, если для отображения битов в символы применяется код Грея [12]. Последняя формула дает РВ=7,310-6, что вполне удовлетворяет требованиям к вероятности появления битовых ошибок. Таким образом, в приведенном примере кодирование с коррекцией ошибок не потребовалось и 8-уровневая PSK удовлетворяет требованиям канала ограниченной полосы пропускания (что и было предсказано при изучении значений Eb|N0 в табл. 9.1).

9.7.6. Система ограниченной мощности без кодирования

Рассмотрим теперь систему, где требуется такая же скорость передачи данных и такая же вероятность появления битовой ошибки, как и в случае, описанном в разделе 9.7.5. Однако в данном примере доступная полоса пропускания W пусть будет равна 45 кГц, а доступное Eb|N0 — 48 дБГц. Как и ранее, задача — выбор схемы модуляции или модуляции/кодирования, которая смогла бы удовлетворить техническим требованиям. В данном случае кодирования с коррекцией ошибок снова не потребуется.

Очевидно, что в этом примере канал не имеет ограничений на полосу пропускания, так как имеющихся 45 кГц полосы более чем достаточно для обеспечения требуемой скорости передачи данных 9600 бит/с. Из уравнения (9.23) получаем принимаемое Eb|N0.

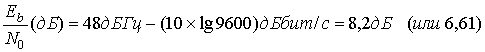(9.28)

Поскольку полоса пропускания избыточна, а для получения нужной вероятности битовой ошибки доступно сравнительно небольшое Eb|N0, канал можно назвать каналом ограниченной мощности. Следовательно, в качестве схемы модуляции выбирается MFSK. Для экономии мощности далее необходимо подобрать максимальное М, при котором минимальная полоса пропускания MFSK не будет превышать доступные 45 кГц. Следуя табл. 9.1, можно видеть, что это возможно при М=16. Следующая задача — выяснить, можно ли удовлетворить требованию РB10-5 с помощью лишь 16-уровневой FSK, без привлечения какого-либо кодирования с коррекцией ошибок. Подобно рассмотренному ранее случаю, из табл. 9.1 видно, что 16-уровневая FSK может удовлетворить требованиям, поскольку требуемое Eb|N0, взятое для 16-уровневой FSK, меньше полученного из уравнения (9.28). Тем не менее мы получим данный результат, не обращаясь к табл. 9.1. Покажем, как определить, нужно ли кодирование с коррекцией ошибок.

Как и ранее, блочная диаграмма на рис. 9.8 отображает соотношение между скоростью передачи символов RS и скоростью передачи битов R и между ES|N0 и Eb|N0 эти соотношения аналогичны полученным в предыдущем примере системы ограниченной полосы. В данном случае демодулятор 16-уровневой схемы FSK принимает сигнал (одну из 16 возможных частот) за интервал TS. При некогерентной MFSK вероятность возникновения в демодуляторе символьной ошибки аппроксимируется следующим выражением [13].

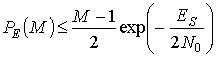(9.29)

Для вычисления PE(М) из формулы (9.29) требуется, как и в предыдущем примере, найти ES|N0. Подставляя выражение (9.28) в (9.26) при М=16, получаем следующее.

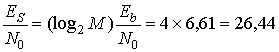(9.30)

Далее формулу (9.30) подставляем в (9.29), что дает вероятность появления символьной ошибки РЕ=1,410-5. Для преобразования этой величины в вероятность появления битовой ошибки РB нужно воспользоваться соотношением между РB и РЕ для передачи ортогональных сигналов [13], которое имеет следующий вид.

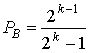(9.31)

Из последней формулы получаем, что РB=7,310-6; это вполне удовлетворяет требуемой вероятности появления битовых ошибок. Таким образом, с помощью 16-уровневой FSK можно удовлетворить требованиям спецификации данного канала ограниченной мощности, не используя дополнительно никакого кодирования с коррекцией ошибок (что и было предсказано при изучении значений Eb|N0 в табл. 9.1).

9.7.7. Система ограниченной мощности и полосы пропускания с кодированием

В этом примере начальные параметры будут такими же, как и в предыдущем примере системы ограниченной полосы пропускания (раздел 9.7.5), а именно W=4000 Гц, Pr|N0=53 дБГц и R=9600 бит/с, за одним исключением. В данном случае предполагается, что вероятность появления битовой ошибки должна быть не больше 10-9. Поскольку полоса пропускания составляет 4000 Гц, а из уравнения (9.23) находим Eb|N0=13,2 дБ, то из табл. 9.1 ясно, что данная система ограничена и по полосе пропускания и по доступной мощности (для удовлетворения требованиям к полосе пропускания можно использовать 8-уровневую схему PSK; но имеющихся 13,2 дБ отношения Eb|N0 совсем не достаточно для обеспечения требуемой вероятности появления битовой ошибки 10-9). При таких малых значениях РB, системы, изображенной на рис. 9.8, явно недостаточно, значит, надо посмотреть, какое повышение производительности сможет дать кодирование с коррекцией ошибок (в пределах доступной полосы пропускания). В общем случае можно использовать сверточный или блочный код. Для упрощения будем применять блочный код. Коды Боуза-Чоудхури-Хоквенгема (Bose, Chaudhuri, Hocquenghem — ВСН, БХЧ) образуют большой класс мощных циклических (блочных) кодов коррекции ошибок [14]. В данном примере выберем из семейства кодов один конкретный. Рассмотрим табл. 9.2, где приведены некоторые коды БХЧ, определяемые параметрами п, k и г. Здесь k — количество информационных битов, которые код преобразует в более длинные блоки из п кодовых битов (их также называют канальными битами или канальными символами), a t - максимальное число неправильных канальных битов, не поддающихся исправлению, в блоке размером и бит. Степень кодирования кода определяется как отношение k/n; а величина, обратная данной, является мерой избыточности кода.

Таблица 9.2. Коды БХЧ (неполный перечень)

n

k

t

7

4

1

15

11

1

7

2

5

3

31

26

1

21

2

16

3

11

4

63

5

57

1

51

2

45

3

39

4

36

5

30

6

127

120

1

113

2

106

3

99

4

92

5

85

6

78

7

71

9

64

10

57

11

50

13

43

14

36

15

29

21

22

23

15

27

8

31

Поскольку ограничения системы аналогичны использованным в разделе 9.7.5, удовлетворить требования к полосе пропускания можно с помощью 8-уровневой схемы PSK. Тем не менее для снижения вероятности появления ошибки до РB 10-9 придется воспользоваться кодом коррекции ошибок. При выборе оптимального кода из табл. 9.2 нужно иметь в виду следующее.

1. Выходная вероятность появления битовой ошибки в комбинированной системе модуляции/кодирования должна удовлетворять системным требованиям достоверности передачи.

2. Степень кодирования кода не должна требовать увеличения полосы пропускания до значения, большего доступного.

3. Код должен быть максимально простым. Вообще, чем короче код, тем проще его реализовать.

Минимальная полоса пропускания для 8-уровневой схемы PSK без кодирования составляет 3200 Гц (см. табл. 9.1), а доступная полоса пропускания канала — 4000 Гц. Следовательно, полосу пропускания некодированного сигнала можно увеличить не более чем в 1,25 раза (или расширить на 25%). Таким образом, самым первым шагом в данном (упрощенном) примере выбора кода будет отбрасывание тех кодов из табл. 9.2, которые потребуют расширения полосы пропускания более чем на 25%. В результате мы получим набор кодов, "совместимых" с полосой пропускания (табл. 9.3). В этой таблице добавлены два столбца, которые обозначены как "эффективность кодирования", G, причем эта величина определяется следующим образом.

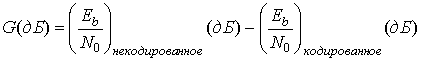(9.32)

Таблица 9.3. Коды БЧХ, «совместимые» с полосой пропускания.

Эффективность кодирования, G(дБ)

n

k

t

PB=10-5

PB=10-9

31

26

1

1,8

2,0

63

57

1

1,8

2,2

51

2

2,6

3,2

127

120

1

1,7

2,2

113

2

2,6

3,4

106

3

3,1

4,0

Из уравнения (9.32) эффективность кодирования можно описать как меру снижения величины требуемого Eb|N0 (в децибелах), которую нужно обеспечить с помощью свойств кода, касающихся обнаружения и исправления ошибок. Эффективность кодирования зависит от типа модуляции и вероятности возникновения битовых ошибок. В табл. 9.3 эффективность кодирования G рассчитана для значений РB=10-5 и РB=10-9. При модуляции MPSK, G относительно независима от значения М. Следовательно, при конкретной вероятности возникновения битовой ошибки данный код будет иметь приблизительно равную эффективность с любой модуляцией MPSK. Эффективность кодирования в табл. 9.3 рассчитана согласно процедуре, описываемой в разделе 9.7,7.1.

На рис. 9.9 изображена блочная диаграмма, включающая кодер и модулятор/демодулятор (модем). Если сравнить рис. 9.9 и 9.8, то видно, что введение блоков кодера/декодера влечет за собой дополнительные преобразования. На рис. 9.9 в блоке кодер/модулятор показано, как преобразовывается скорость передачи: из R (бит/с) в RC (канальных бит/с), а затем в RS (символ/с).

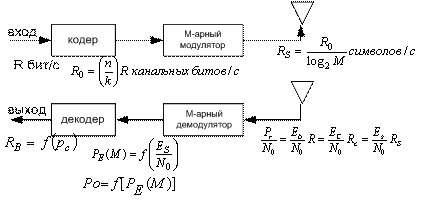
Рис. 9.9. Схема модема с канальным кодированием

Предполагается, что рассматриваемая система связи является системой реального времени, а значит, в ней недопустимы задержки при передаче сообщений. Следовательно, скорость передачи канальных битов RC должна превышать битовую скорость передачи данных R в n/k раз. Более того, каждый передаваемый символ образован (log2 M) канальными битами, так что символьная скорость передачи RS меньше RC в (log2 M) раз. Для систем с модуляцией и кодированием преобразования скорости имеют следующий вид.

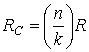(9.33)

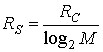(9.34)

В блоке демодулятор/декодер, показанном на рис. 9.9, преобразования энергии битов данных, энергии канальных битов и энергии символов связаны теми же множителями, что и преобразования скоростей, показанные в выражениях (9.33) и (9.34). Поскольку при преобразовании кодирования k информационных битов заменяются п канальными битами, отношение энергии канального бита к спектральной плотности мощности шума, Ec|N0, — это результат умножения Eb|N0 на коэффициент k/n. Кроме того, поскольку каждый передаваемый символ состоит из (log2M) канальных битов, ES|N0, необходимое в (9.25) для получения РЕ, вычисляется путем умножения Ec|N0 на коэффициент (log2M). Для систем, содержащих одновременно и модуляцию, и кодирование, преобразования отношений энергии к спектральной плотности мощности шума будут следующими.

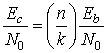(9.35)

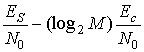(9.36)

Следовательно, исходя из уравнений (9.33)—(9.36), можно обобщить выражение для Pr|N0 в уравнении (9.24).

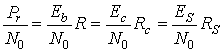(9.37)

Как и ранее, канал связи описывается величиной Eb|N0, выражаемой в децибелах. Тем не менее на входе демодулятора/детектора нет ни информационных, ни канальных битов. Есть только сигналы (символы передачи), которым присваивается битовое значение, а следовательно, их можно описывать через пропорциональное распределение энергии по битам. Из формулы (9.37) видно, что додетекторная точка приемника — это удобная опорная точка, в которой можно соотнести эффективную энергию и эффективную скорость различных параметров. Слово "эффективный" используется потому, что единственные сигналы в додетекторной точке — это импульсы, которые мы называем символами. Конечно, эти символы связаны с канальными битами, которые, в свою очередь, связаны с информационными битами. Чтобы подчеркнуть тот момент, что уравнение (9.37) весьма удобно при учете системных ресурсов, рассмотрим систему, в которой поток некоторого числа битов, например 273 бит, настолько часто появляется в виде отдельного блока, что этой группе присваивается собственное имя; все это идет отдельной "порцией". Инженеры делают это постоянно, например восемь бит называют байтом. Как только мы определили новый объект, его сразу можно связать с параметрами уравнения (9.37), поскольку Pr|N0 — это теперь энергия блока на N0, умноженная на скорость передачи блока. Нечто такое будет использовано в главе 12, где подобное расширение формулы (9.37) будет применяться к элементарным сигналам расширенного спектра.

Поскольку значения Pr|N0 и R равны 53 дБГц и 9600 бит/с, (по аналогии с предыдущим случаем) из уравнения (9.23) находим, что принятое Eb|N0= 13,2 дБ. Отметим, что принимаемое Eb|N0 фиксированно и не зависит от параметров кода n и k, а также от параметра модуляции M. Как было установлено при изучении табл. 9.3, для идеального кода, удовлетворяющего всем требованиям, можно итеративно повторить расчеты, представленные на рис. 9.9. Полезно запрограммировать на ПК (или калькуляторе) следующие четыре шага как функцию от п, k и t. Шаг первый начинается с подстановки уравнения (9.35) в (9.36).

Шаг 1 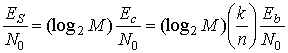(9.38)

Шаг 2 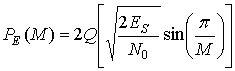(9.39)

Выражение (9.39) — это аппроксимация (для М-арной PSK) вероятности символьной ошибки РЕ, которая уже приводилась в формуле (9.25). В каждый промежуток передачи символа демодулятор принимает решение относительно значения символа и подает на декодер последовательность канальных битов, представляющую этот символ. Если на демодуляторе канальные биты квантуются на два уровня, обозначаемых 1 и 0, говорят, что демодулятор принимает жесткое решение (hard decision). Если выход демодулятора квантуется более чем на два уровня — демодулятор принимает мягкое решение (soft decision). В этом разделе предполагается принятие жестких решений.

Теперь, когда в системе присутствует блок декодера, вероятность появления ошибки в канальном бите вне демодулятора и на декодере будем обозначать как pc а вероятность появления ошибки в бите вне декодера, как и ранее, будем обозначать через РВ(декодированная вероятность битовой ошибки). С помощью рсуравнение (9.27) можно переписать следующим образом.

Шаг 3 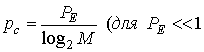(9.40)

Третий шаг связывает вероятность появления ошибки в канальном бите с вероятностью появления ошибки в символе вне демодулятора (предполагается использование кода Грея, как это было в уравнении (9.27)).

В системах связи реального времени, использующих традиционные схемы кодирования, при фиксированном значении Pr|N0 величина ES|N0 с кодированием всегда будет меньше величины ES|N0 без кодирования. Поскольку при кодировании демодулятор принимает сигнал с меньшим ES|N0, он делает больше ошибок! Тем не менее при использовании кодирования достоверность передачи зависит от характеристик не только демодулятора, но и декодера. Следовательно, для повышения достоверности передачи при кодировании декодер должен осуществлять коррекцию ошибок так, чтобы перекрывать слабую производительность демодулятора. Итоговая декодированная вероятность битовой ошибки РВна выходе зависит от конкретного кода, декодера и вероятности появления ошибки в канальном бите рс. Эту зависимость можно аппроксимировать следующим выражением [15].

Шаг 4 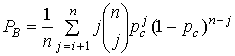(9.41)

На четвертом шаге t — это наибольшее число канальных битов, которые код способен исправить в блоке размером п бит. Исходя из уравнений (9.38)-(9.41), определяющих четыре упомянутых выше шага, декодированную вероятность появления битовой ошибки РB можно рассчитать как функцию п, k и t для всех кодов, представленных в табл. 9.3. Нужная позиция таблицы, удовлетворяющая установленным требованиям к вероятности возникновения ошибки с наибольшей возможной степенью кодирования и наименьшим п, — это код с коррекцией двойных ошибок (63, 51). Ниже приводятся соответствующие расчеты.

Шаг 1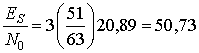

где М = 8, а принятое Eb|N0 = 13,2 дБ (или 20,89).

Шаг 2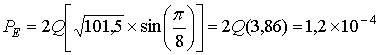

Шаг 3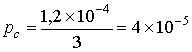

Шаг 4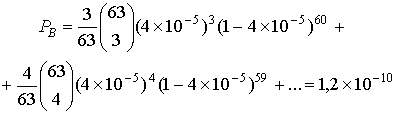

На четвертом шаге способность кода к исправлению битовых ошибок t=2. Для получения РB на четвертом шаге, учитываются только первые два члена суммы в уравнении (9.41), так как остальные слагаемые дают пренебрежимо малый вклад при малых значениях рсили при разумно большом Eb|N0. Важно отметить, что при выполнении этих расчетов на компьютере стоит (на всякий случай) всегда учитывать все слагаемые в формуле (9.41), так как приближенное решение может сильно отличаться от правильного при малых значениях Eb|N0. Теперь, когда мы выбрали код (63, 51), рассчитаем скорость передачи данных в канальных битах Rc и скорость передачи символов RS с помощью уравнений (9.33) и (9.34), при М = 8.

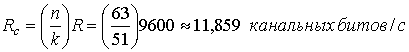
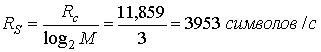
9.7.7.1. Расчет эффективности кодирования

Более прямой способ поиска простейшего кода, удовлетворяющего требованиям, указанным в разделе 9.7.7, состоит в следующем. Вначале для схемы 8-PSK без кодированиярассчитывается, насколько большее (относительно доступных 13,2 дБ) значение Eb|N0 требуется для получения РВ=10-4. Это дополнительное Eb|N0 является требуемой эффективностью кодирования. Используя формулы (9.27) и (9.39), находим ES|N0 без использования кодирования, которое даст вероятность появления ошибки РВ=10-9.

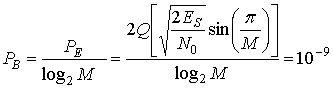(9.42)

При таком низком значении вероятности битовой ошибки, правомерно использовать приведенную в (3.44) аппроксимацию Q(x). Методом проб и ошибок (с помощью программируемого калькулятора) находим, что Eb|N0 без кодирования равно 120,67 (20,8 дБ), и поскольку каждый символ состоит из (1оg2 8)=3 бит, требуемое (Eb|N0) (без кодирования)= 120,67/3=40,22=16дБ. Из параметров примера и уравнения (9.23) мы знаем, что (E,JN0) (с кодированием) = 13,2 дБ. Следовательно, используя формулу (9.32), видим, что эффективность кодирования, удовлетворяющая условию РB = 10-9, равна следующему.

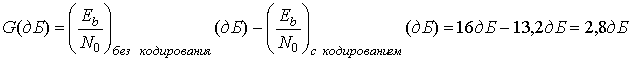
Чтобы приведенный выше расчет был точным, все значения Eb|N0 должны точно соответствовать одинаковым значениям вероятности битовой ошибки. В нашей ситуации это не совсем так: два значения Eb|N0 соответствуют РB =10-9 и РB=1,210-10. Тем не менее при таких низких значениях вероятности (даже при таком отличии) расчеты дают хорошее приближенное значение требуемой эффективности кодирования. Изучая табл. 9.3 на предмет выбора простейшего кода, дающего эффективность кодирования не меньше 2,8 дБ, видим, что это код (63, 51); тот же, что и был выбран ранее. Отметим, что эффективность кодирования нужно всегда определять для конкретной вероятности появления ошибки и типа модуляции, как в табл. 9.3.

9.7.7.2. Выбор кода

Рассмотрим систему связи реального времени, которая, согласно спецификации, относится к системам ограниченной мощности, но в то же время обладает достаточной полосой пропускания и должна иметь очень низкую вероятность возникновения ошибки. В данной ситуации необходимо кодирование с коррекцией ошибок. Пусть для кодирования нужно выбрать один из кодов БХЧ, которые представлены в табл. 9.2. Поскольку система имеет достаточную полосу пропускания, а требования относительно вероятности ошибок довольно строги, может возникнуть соблазн выбора самого мощного кода, из указанных в табл. 9.2, а именно — кода (127, 8), способного исправлять комбинации до 31 искаженных бит в блоке размером 127 кодовых бит. Будет ли кто-либо использовать такой код в системе связи реального времени? Конечно же, нет. Объясним, почему такой выбор неразумен.

Если в системе связи реального времени применяется код коррекции ошибок, то на достоверность передачи оказывают влияние два фактора. Один вызывает улучшение достоверности передачи, а другой — снижение. Первый фактор — это кодирование; чем больше избыточность кода, тем выше способность кода к коррекции ошибок. Второй фактор — это уменьшение энергии, приходящейся на канальный символ или кодовый бит (по сравнению с информационным битом). Такое уменьшение энергии вызвано повышением избыточности (что влечет за собой увеличение скорости передачи в системе связи реального времени). Меньшая энергия символа — это большее число ошибок. В конце концов, второй фактор подавляет первый, и при очень низких степенях кодирования резко возрастает вероятность появления ошибки. (Эти рассуждения иллюстрируются ниже, в примере 9.4.) Следует отметить, что сказанное справедливо только для систем связи реального времени, где задержки передачи сообщения недопустимы. В иных системах можно "играть на компромиссах" между задержкой при передаче сообщения и избыточностью кода (не снижая энергию, приходящуюся на символ).

Пример 9.4. Выбор кода, удовлетворяющего требованиям спецификации

Даны следующие параметры системы: Pr|N0=67дБГц, скорость передачи данных R=106 бит/с, доступная полоса пропускания W=20 МГц, декодированная вероятность битовой ошибки PB10-7, модуляция BPSK. Выберите из табл. 9.2 код, удовлетворяющий этим требованиям. Рассмотрение начать с кода (127, 8). Привлекательность этого кода объясняется наивысшей (из представленных кодов) способностью к коррекции ошибок.

Решение

Код (127,8) расширяет полосу пропускания в 127/8=15,875 раз. Следовательно, при использовании этого кода скорость передачи 1 Мбит/с (определяющая номинальную полосу пропускания в 1 МГц) возрастает до 15,875 МГц. Таким образом, передаваемый сигнал находится в пределах полосы 20 МГц, что позволяет увеличение полосы еше на 25% для целей фильтрации. После выбора кода оценим вероятность ошибки, использовав шаги, описанные в разделе 9.7.7.

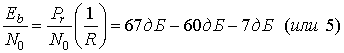
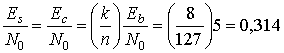
Поскольку применяется двоичная модуляция, рс=РЕ, так что имеем следующее.

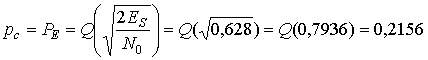
Код (127,8) способен исправлять последовательности до t=31 ошибочных бит, поэтому, используя формулу (9.41), получаем следующую вероятность появления ошибки в декодированном бите.

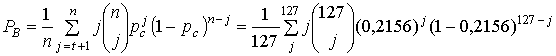
При очень малом рсдостаточно взять лишь первые несколько членов суммы. Но если рс большое, как в данном случае, то помощь компьютера будет очень кстати. После выполнения расчетов с рс=0,2156 вероятность появления ошибки в декодированном бите РB получаем равной 0,05, что очень сильно отличается от требуемых 10-7. Возьмем теперь код, степень кодирования которого близка к очень популярному значению 1/2, т.е. код (127, 64). Возможности этого кода не столь значительны, как у первого кода. Он может исправить 10 искаженных битов в блоке из 127 кодовых битов. Впрочем, исследуем этот код. Выполняя те же шаги, что и выше, получаем следующее.

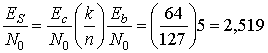
Отметив, насколько большее ES|N0 получено, по сравнению с кодом (127, 8), продолжим вычисление.

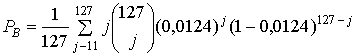
В итоге, РB=5,610-8, что удовлетворяет системным требованиям. Из этого примера можно видеть, что выбор кода нужно делать, рассматривая тип модуляции и имеющееся Eb|N0 . При выборе можно руководствоваться тем, что очень высокие и очень низкие степени кодирования, в основном, оказываются малоэффективными в системах связи реального времени, что ясно видно из поведения кривых на рис. 8.6 (глава 8).