9.8.1. Передача сигналов с модуляцией QPSK и OQPSK

9.8.2. Манипуляция с минимальным сдвигом

9.8.2.1.Вероятность ошибки при модуляциях OQPSK и MSK

9.8.3. Квадратурная амплитудная модуляция

9.8.3.1. Вероятность битовой ошибки при модуляции QAM

9.8.3.2. Компромисс между полосой пропускания и мощностью

Основной задачей спектрально эффективных модуляций является максимизация эффективности использования полосы частот. Увеличение спроса на цифровые каналы передачи привело к исследованиям спектрально эффективных методов модуляции [8, 16], направленных на максимально эффективное использование полосы частот и, следовательно, призванных ослабить проблему спектральной перегрузки каналов связи.

В некоторых системах, помимо требования эффективности использования спектра, имеются и другие. Например, в спутниковых системах с сильно нелинейными транс-пондерами требуется модуляция с постоянной огибающей. Это связано с тем, что при прохождении сигнала с большими флуктуациями амплитуды нелинейные транспондеры создают паразитные боковые полосы (причина — механизм, называемый преобразованием амплитудной модуляции в фазовую). Эти боковые полосы отбирают у информационного сигнала часть мощности транспондера, а также могут интерферировать с сигналами соседних каналов (помеха соседнего канала) или других систем связи (внутриканальная помеха). Двумя примерами модуляций с постоянной огибающей, подходящими для систем с нелинейными транспондерами, являются квадратурная фазовая манипуляция со сдвигом (Offset QPSK — OQPSK) и манипуляция с минимальным сдвигом (minimum shift keying — MSK).

9.8.1. Передача сигналов с модуляцией QPSK и OQPSK

На рис. 9.10 показано разбиение типичного потока импульсов при модуляции QPSK. На рис. 9.10, а представлен исходный поток данных dk(t)=d0,d1,d2, ..., состоящий из биполярных импульсов, т.е. dk принимают значения +1 или -1, представляющие двоичную единицу и двоичный нуль. Этот поток импульсов разделяется на синфазный поток, dI(t), и квадратурный, dQ(t), как показано на рис. 9.10, б.

dI(t) = d0, d2, d4, ... (четные биты)

dQ(t) = d1, d3, d5, ... (нечетные биты)

Отметим, что скорости потоков dI(t) и dQ(t) равны половине скорости передачи потока dk(t). Удобную ортогональную реализацию сигнала QPSK, s(t), можно получить, используя амплитудную модуляцию синфазного и квадратурного потоков на синусной и косинусной функциях от несущей.

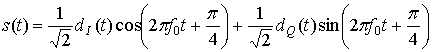(9.44)

С помощью тригонометрических тождеств (Г.5) и (Г.6) уравнение (9.44) можно представить в следующем виде.

(9.45)

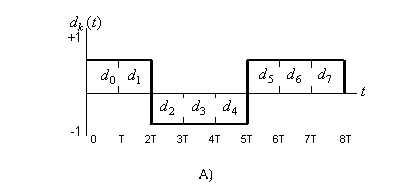
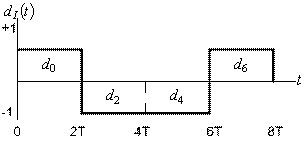
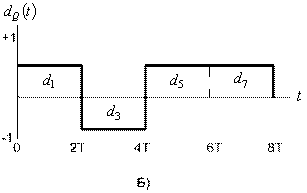
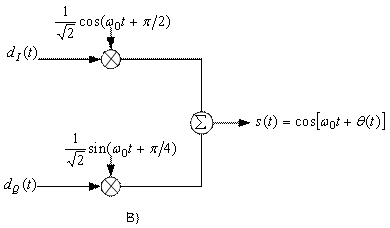
Рис.9.10. Модуляция QPSK

Модулятор QPSK, показанный на рис. 9.10, в, использует сумму синусоидального и косинусоидального слагаемых, тогда как аналогичное устройство, описанное в разделе 4.6, применяет разность таких слагаемых. Материл данного раздела представлен так, как это сделано в работе [17]. Поскольку когерентный приемник должен разрешать любую неопределенность фазы, использование в передатчике иного формата фазы можно рассматривать как часть подобной неопределенности. Поток импульсов dI(t) используется для амплитудной модуляции (с амплитудой +1 или -1) косинусоиды. Это равноценно сдвигу фазы косинусоиды на 0 или ; следовательно, в результате получаем сигнал BPSK. Аналогично поток импульсов dQ(t) модулирует синусоиду, что дает сигнал BPSK, ортогональный предыдущему. При суммировании этих двух ортогог нальных компонентов несущей получается сигнал QPSK. Величина будет соответствовать одному из четырех возможных сочетаний dI(t) и dQ(t) в уравнении (9.44): = 0°, ±90° или 180°; результирующие векторы сигналов показаны в сигнальном пространстве на рис. 9.11. Так как cos() и sin() ортогональны, два сигнала BPSK можно обнаруживать раздельно.

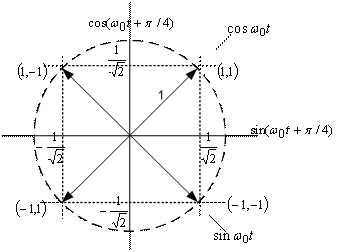
Рис. 9.11. Сигнальное пространство для схем QPSK и OQPSK

Передачу сигналов OQPSK также можно представить формулами (9.44) и (9.45); различие между двумя схемами модуляции, QPSK и OQPSK, состоит только в ориентации двух модулированных сигналов. Как показано на рис. 9.10, длительность каждого исходного импульса равна Т (рис.9.10, а); следовательно, в потоках на рис. 9.10, б длительность каждого импульса равна 2T. В обычной QPSK потоки четных и нечетных импульсов передаются со скоростью 1/(2T) бит/с, причем они синхронизированы так, что их переходы совпадают, как показано на рис. 9.10, б. В OQPSK, которую иногда называют QPSK с разнесением (staggered QPSK — SQPSK), используется также разделение потока данных и ортогональная передача; разница в том, что потоки dI(t) и dQ(t) синхронизированы со сдвигом на Т. Этот сдвиг показан на рис. 9.12.

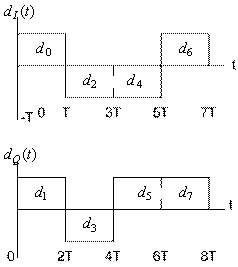
Рис. 9.12. Потоки данных при модуляции OQPSK

При стандартной QPSK из-за синхронизации dI(t) и dQ(t) за промежуток 2Т фаза несущей может изменяться только раз. В зависимости от значений dI(t) и dQ(t) в любом промежутке 2Т, фаза несущей на этом промежутке может принимать одно из четырех значений, показанных на рис. 9.11. В течение следующего интервала 2T фаза несущей остается такой же, если ни один из потоков не меняет знака. Если только один из потоков импульсов изменит знак, происходит сдвиг фазы на ±90°. Изменение знака у обоих потоков приводит к сдвигу фазы на 180°. На- рис. 9.13, а изображен типичный сигнал QPSK для последовательности dI(t) и dQ(t), показанной на рис. 9.10.

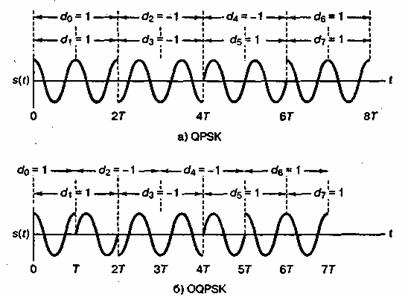
Рис. 9.13. Сигналы: a) QPSK; 6) OQPSK. (Перепечатано с разрешения автора из работы Pasupathy S. "Minimum Shift Keying: A Spectrally Efficient Modulation," IEEE Commun. Mag., July, 1979, Fig. 4, p. 17. © 1979, IEEE.)

Если сигнал, модулированный QPSK, подвергается фильтрации для уменьшения побочных максимумов спектра, результирующий сигнал больше не будет иметь постоянной огибающей и, фактически, случайный фазовый сдвиг на 180° вызовет моментальное обращение огибающей в нуль (рис. 9.13, а). Если эти сигналы применяются в спутниковых каналах, где используются нелинейные усилители, постоянная огибающая будет восстанавливаться. Однако в то же время восстанавливаться будут и все нежелательные частотные боковые максимумы, которые могут интерферировать с сигналами соседних каналов и других систем связи.

При модуляции QPSK потоки импульсов dI(t) и dQ(t) разнесены и, следовательно, не могут одновременно изменить состояние. Несущая не может изменять фазу на 180°, поскольку за один раз переход может сделать только один из компонентов. За каждые Т секунд фаза может измениться только на 0° или ±90°. На рис. 9.13, б показан типичный сигнал OQPSK для последовательности, представленной на рис. 9.12. Если сигнал OQPSK становится сигналом с ограниченной полосой, возникающая межсимвольная интерференция приводит к легкому спаду огибающей в области переходов фазы на ±90°, но поскольку переходов на 180° при OQPSK нет, огибающая не обращается в нуль, как это происходит при QPSK. Если сигнал OQPSK с ограниченной полосой проходит через нелинейный транспондер, спад огибающей устраняется; в то же время высокочастотные компоненты, связанные с исчезновением огибающей, не усиливаются. Таким образом, отсутствует внеполосная интерференция [17].

9.8.2. Манипуляция с минимальным сдвигом

Главное преимущество OQPSK перед QPSK. (устранение внеполосной интерференции) наводит на мысль, что можно дополнительно усилить формат OQPSK, устранив разрывные переходы фазы. Это стало мотивацией разработки схем модуляции без разрыва фазы (continuous phase modulation — СРМ). Одной из таких схем является манипуляция с минимальным сдвигом (minimum shift keying — MSK) [17, 20]. MSK можно рассматривать как частный случай частотной манипуляции без разрыва фазы (continuous-phase frequency shift keying — CPFSK) или как частный случай OQPSK с синусоидальным взвешиванием символов. В первом случае сигнал MSK можно представить следующим образом [18].

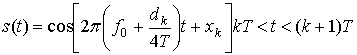(9.46)

Здесь f0— несущая частота, dk=±1 представляет биполярные данные,* которые передаются со скоростью R = 1|T, a xk — это фазовая постоянная для k-го интервала передачи двоичных данных. Отметим, что при dk=1 передаваемая частота — это f0+1/4T, а при dk=-1 — этоf0-1/4T. Следовательно, разнесение тонов в MSK составляет половину от используемого при ортогональной FSK с некогерентной демодуляцией, откуда и название — манипуляция с минимальным сдвигом. В течение каждого Т-секундного интервала передачи данных значение xk постоянно, т.е. xk=0 или , что диктуется требованием непрерывности фазы сигнала в моменты t=kT. Это требование накладывает ограничение на фазу, которое можно представить следующим рекурсивным соотношением для xk.

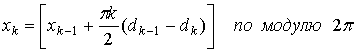(9.47)

С помощью тождеств (Г.5) и (Г.6) уравнение (9.46) можно переписать в квадратурном представлении.

(9.48)

где

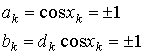(9.49)

Синфазный компонент обозначается как , где - несущая, - синусоидальное взвешивание символов, ak — информационно-зависимый член. Подобным образом квадратурный компонент — это, где — квадратурное слагаемое несущей, — такое же синусоидальное взвешивание символов, a bk — информационно-зависимый член. Может показаться, что величины ak и bk могут изменять свое значение каждые Т секунд. Однако из-за требования непрерывности фазы величина ak может измениться лишь при переходе функции через нуль; - a bk — только при переходе через нуль . Следовательно, взвешивание символов в синфазном или квадратурном канале — это синусоидальный импульс с периодом 2Т и переменным знаком. Как и в случае OQPSK, синфазный и квадратурный компоненты сдвинуты относительно друг друга на Т секунд.

Отметим, что xk в уравнении (9.46) — это функция разности между прежним и текущим информационными битами (дифференциальное кодирование). Таким образом, величины ak и bk в уравнении (9.48) можно рассматривать как дифференциально кодированные компоненты исходных данных dk - Однако чтобы биты данных dk были независимы между собой, знаки последовательных импульсов квадратурного и синфазного каналов различных интервалов, длительностью, 2Т секунд, должны быть случайными импульсами. Таким образом, если уравнение (9.48) рассматривать как частный случай модуляции OQPSK, его можно переписать в иной (недифференциальной) форме [18].

(9.50)

Здесь dI(t) и dQ(t) имеют такой же смысл синфазного и квадратурного потоков данных, как и в уравнении (9.43). Схема MSK, записанная в форме (9.50), иногда называется MSK с предварительным кодированием (preceded MSK). Графическое представление уравнения (9.50) дано на рис. 9.14. На рис. 9.14, а и в показано синусоидальное взвешивание импульсов синфазного и квадратурного каналов. Эти последовательности представляют собой те же информационные последовательности, что и на рис. 9.12, но здесь умножение на синусоиду дает более плавные переходы фазы, чем в исходном представлении данных. На рис. 9.14, б и г показана модуляция ортогональных компонентов и синусоидальными потоками данных. На рис. 9.14, д представлено суммирование ортогональных компонентов, изображенных на рис. 9.14, б и г. Итак, из уравнения (9.50) и рис. 9.14 можно заключить следующее: 1) сигнал s(t) имеет постоянную огибающую; 2) фаза радиочастотной несущей непрерывна при битовых переходах; 3) сигнал s(t) можно рассматривать как сигнал, модулированный FSK, с частотами передачи f0+1/4T и f0-1/4T. Таким образом, минимальное разнесение тонов, требуемое при модуляции MSK, можно записать следующим образом.

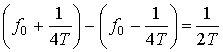. (9.51)

что равно половине скорости передачи битов. Отметим, что разнесение тонов, требуемое для MSK, — это половина (1/T) разнесения, необходимого при некогерентном обнаружении сигналов, модулированных FSK (см. раздел 4.5.4). Это объясняется тем, что фаза несущей известна и непрерывна, что позволяет осуществить когерентную демодуляцию сигнала.

Спектральная плотность мощности G(f) дляQPSK и OQPSK имеет следующий вид [18].

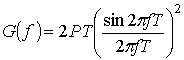(9.52)

где Р — средняя мощность модулированного сигнала. При MSK G(f) будет иметь следующий вид [18].

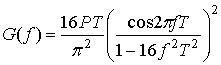(9.53)

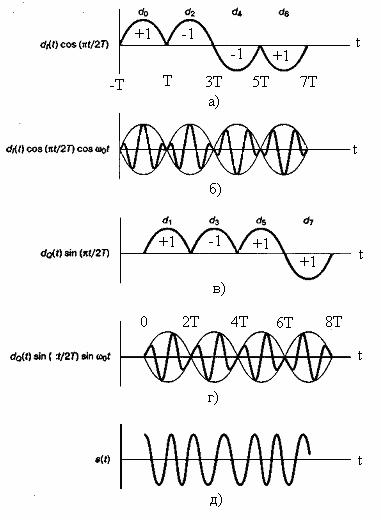
Рис. 9.14. Манипуляция с минимальным сдвигом (minimum shift keying — MSK): а) модифицированный синфазный поток битов; 6) произведение синфазного потока битов и несущей; в) модифицированный квадратурный поток битов; г) произведение квадратурного потока битов и несущей; д) сигнал MSK. (Перепечатано с разрешения автора из работы Pasupathy S. "Minimum Shift Keying: A Spectrally Efficient Modulation," IEEE Common. Mag., July, 1979, Fig. 5, p. 18. © 1979, IEEE.)

Нормированная спектральная плотность мощности (P=1Вт) для QPSK, OQPSK и MSK изображена на рис. 9.15. Для сравнения здесь же приводится спектральный график BPSK. Не должно удивлять, что BPSK требует большей полосы пропускания, чем другие типы модуляции, при том же уровне спектральной плотности. В разделе 9.5.1 и на рис. 9.6 было показано, что теоретическая эффективность использования полосы частот схемы BPSK вдвое меньше, чем схемы QPSK. Из рис. 9.15 видно, что боковые максимумы графика MSK ниже, чем графика QPSK или OQPSK. Это является следствием умножения потока данных на синусоиду и дает большое количество плавных фазовых переходов. Чем плавнее переход, тем быстрее спектральные хвосты стремятся к нулю. Модуляция MSK спектрально эффективнее QPSK или OQPSK; тем не менее, как видно из рис. 9.15, спектр MSK имеет более широкий основной максимум, чем спектр QPSK или OQPSK. Следовательно, MSK нельзя назвать удачным выбором при наличии узкополосных линий связи. В то же время MSK стоит использовать в системах с несколькими несущими, поскольку ее относительно малые побочные максимумы спектра позволяют избежать значительных помех соседних каналов (adjacent channel interference — ACI). To, что спектр QPSK имеет более узкий основной максимум, чем MSK, объясняется тем, что при данной скорости передачи битов скорость передачи символов QPSK вдвое меньше скорости передачи символов MSK.

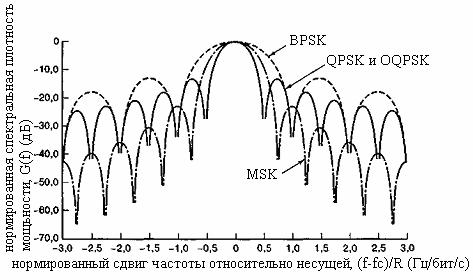
Рис. 9.15. Нормированная спектральная плотность мощности для BPSK, QPSK, OQPSK и MSK. (Перепечатано с разрешения автора из работы Amoroso F. "The Bandwidth of Digital Data Signals, " IEEE Commun. Mag., vol. 18, n. 6, November, 1980, Fig. 24, p. 16. © 1980, IEEE.)

9.8.2.1. Вероятность ошибки при модуляциях OQPSK и MSK

Ранее говорилось, что BPSK и QPSK имеют одинаковую вероятность появления битовой ошибки, поскольку QPSK сконфигурирована как два сигнала BPSK на ортогональных компонентах несущей. Так как разнесение потоков данных не меняет ортогональности несущих, схема OQPSK имеет ту же теоретическую вероятность появления битовой ошибки, что и BPSK и QPSK.

Для модуляции двух квадратурных компонентов несущей манипуляция с минимальным сдвигом использует сигналы антиподной формы, и , с периодом 2Т. Следовательно, если для независимого восстановления данных из каждого ортогонального компонента используются согласованные фильтры, то модуляция MSK, определенная в формуле (9.50), имеет ту же вероятность появления ошибки, что и BPSK, QPSK и OQPSK [17]. Однако если сигнал, модулированный MSK, когерентно обнаруживается в интервале Т секунд как сигнал, модулированный FSK, то эта вероятность будет ниже, чем у BPSK, на 3дБ [17]. У MSK с дифференциально кодированными данными, определенной в выражении (9.46), вероятность появления ошибки будет такой же, как и при когерентном обнаружении дифференциально кодированных данных в модуляции PSK. Сигналы MSK также можно обнаруживать некогерентно [19]. Это позволяет осуществлять дешевую демодуляцию (если это позволяет величина принятого Eb/N0).

9.8.3. Квадратурная амплитудная модуляция

Когерентная М-арная фазовая манипуляция (M-ary phase shift keying — MPSK) — Это хорошо известный метод, позволяющий сузить полосу пропускания. Здесь используется не бинарный алфавит с передачей одного информационного бита за период передачи канального символа, а алфавит из М символов, что позволяет передавать k=log2M битов за каждый символьный интервал. Поскольку использование M-арных символов в k раз повышает скорость передачи информации при той же полосе пропускания, то при фиксированной скорости применение М-арной PSK сужает необходимую полосу пропускания в k раз (см. раздел 4.8.3).

Из уравнения (9.44) можно видеть, что модуляция QPSK состоит из двух независимых потоков. Один поток модулирует амплитуду косинусоидальной функции несущей на уровни +1 и -1, а другой — аналогичным образом синусоидальную функцию. Результирующий сигнал называется двухполосным сигналом с подавлением несущей (double-sideband suppressed-carrier — DSB-SC), поскольку полоса радиочастот вдвое больше полосы немодулированного сигнала (см. раздел 1.7.1) и не содержит выделенной несущей. Квадратурную амплитудную модуляцию (quadrature amplitude modulation — QAM) можно считать логическим продолжением QPSK, поскольку сигнал QAM также состоит из двух независимых амплитудно-модулированных несущих. Каждый блок из k бит (k полагается четным) можно разделить на два блока из k/2 бит, подаваемых на цифро-аналоговые преобразователи (ЦАП), которые обеспечивают требующее модулирующее напряжение для несущих. В приемнике оба сигнала обнаруживаются независимо с помощью согласованных фильтров. Передачу сигналов, модулированных QAM, можно также рассматривать как комбинацию амплитудной (amplitude shift keying — ASK) и фазовой (phase shift keying — PSK) манипуляций, откуда альтернативное название амплитудно-фазовая манипуляция (amplitude phase keying — АРК). И наконец, ее можно считать двухмерной амплитудной манипуляцией, откуда еще одно название — квадратурная амплитудная манипуляция (quadrature amplitude shift keying — QASK).

На рис. 9.16, а показано двухмерное пространство сигналов и набор векторов сигналов, модулированных 16-ричной QAM и изображенных точками, которые расположены в виде прямоугольной совокупности. На рис. 9.16, б показан канонический модулятор QAM. На рис. 9.16, в изображен пример модели канала, в которой предполагается наличие лишь гауссова шума. Сигналы передаются в виде пары (x, у). На модели показано, что координаты сигнальной точки (x, у) передаются по раздельным каналам и независимо возмущаются переменными гауссова шума (пx,nу), каждый компонент которого имеет нулевое среднее и дисперсию N. Можно также сказать, что двухмерная точка сигнала возмущается двухмерной переменной гауссова шума. Если средняя энергия сигнала (среднеквадратическое значение координат сигнала) равна S, тогда отношение сигнал/шум равно S/N. Простейший метод цифровой передачи сигналов через подобные системы — это применение одномерной амплитудно-импульсной модуляции (pulse amplitude modulation — РАМ) независимо к каждой координате сигнала. При модуляции РАМ для передачи k битов/размерность по гауссову каналу каждая точка сигнала принимает значение одной из 2^k равновероятных эквидистантных амплитуд. Точки сигналов принято группировать в окрестности пространства на амплитудах ±1, ±3, ..., ±(2^k - 1).

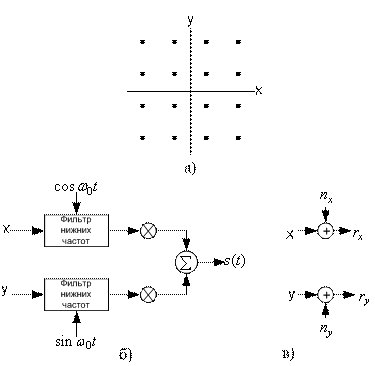
Рис. 9.16. Схема модуляции QAM: а) 16-ричное пространство сигналов; б) канонический модулятор QAM; в) модель канала QAM

9.8.3.1. Вероятность битовой ошибки при модуляции QAM

Для прямоугольной совокупности, гауссова канала и приема с помощью согласованных фильтров, вероятность появления битовой ошибки выражается следующим образом [12].

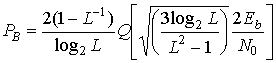(9.54)

Здесь Q(x) определено в формуле (3.43), a L представляет количество уровней амплитуды в одном измерении. Предполагается, что при отображении последовательности log2 L бит в L-арный символ используется код Грея (см. раздел 4.9.4).

9.8.3.2. Компромисс между полосой пропускания и мощностью

На рис. 9.6 представлена плоскость эффективности использования полосы частот, на которой показан компромисс между полосой пропускания и мощностью при Л/арной модуляции QAM, если вероятность битовой ошибки равна 10^-5, а значения на оси абсцисс измеряются в среднем отношении Eb/N0. Предполагается, что немодулированные импульсы фильтруются по Найквисту, так что двусторонняя полоса пропускания на промежуточной частоте (Intermediate Frequency — IF) равна WIF =1/Т, где Т — длительность передачи символа. Следовательно, эффективность использования полосы частот равна R/W= log2 М, где М — размер набора символов. Для реальных каналов и сигналов достоверность передачи ниже указанной, поскольку для реализации реальных фильтров требуется большая полоса пропускания. Из рис. 9.6 видно, что QAM — это метод снижения требований к полосе пропускания при передаче цифровых данных. Как и при M-арной PSK, за счет снижения эффективности использования полосы частот можно получить выигрыш в мощности или Eb/N0; однако при QAM можно реализовать более выгодный компромисс, чем при М-арной PSK.

Пример 9.5. Выбор схемы модуляции

Пусть поток данных со скоростью R=144 Мбит/с передается по радиочастотному каналу с использованием двухполосной схемы модуляции. Предполагается фильтрация по Найквисту и наличие двусторонней полосы 36 МГц. Какую модуляцию стоит выбрать при данных требованиях? Если доступное Eb/N0, равно 20, какой будет вероятность битовой ошибки?

Решение

Запишем требуемую спектральную эффективность.

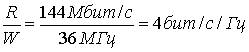
Из рис. 9.6 видно, что 16-ричная QAM с теоретической спектральной эффективностью 4 бит/с/Гц требует более низкого значения Eb|N0, чем 16-арная PSK, при том же значении рв . Исходя из этого выбираем модем QAM.

Считая Eb|N0 равным 20 и используя формулу (9.54), вычисляем ожидаемую вероятность битовой ошибки.

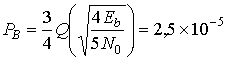
Пример 9.6. Спектральная эффективность

а) Объясните схему расчета спектральной эффективности схемы QAM в примере 9.5, считая что сигнал, модулированный QAM, передается на ортогональных компонентах несущей.

б) Поскольку двусторонняя полоса пропускания в примере 9.5 равна 36 МГц, рассмотрим использование половины этого значения для передачи потока данных со скоростью 144 Мбит/с при многоуровневой схеме РАМ. Какая спектральная эффективность нужна для осуществления этого и какое количество уровней необходимо в схеме РАМ? Предполагается фильтрация по Найквисту.

Решение

а) Полосовой канал с использованием схемы QAM: поток данных со скоростью 144 Мбит/с разделяется на синфазный поток со скоростью 72 Мбит/с и квадратурный поток с такой же скоростью (72 Мбит/с); один поток модулирует амплитуду косинусоидальной функции несущей в полосе пропускания 36 МГц, а другой поток аналогичным образом модулирует синусоидальную функцию. Поскольку каждый поток со скоростью 72 Мбит/с модулирует ортогональный компонент несущей, 36 МГц достаточно для обоих потоков или для передачи со скоростью 144 Мбит/с. Следовательно, спектральная эффективность равна (144 Мбит/с)/36 МГц =4 бит/с/Гц.

б) Требуемая спектральная эффективность при узкополосной передаче равна следующему.

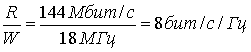
Если предполагается фильтрация по Найквисту, полоса пропускания 18 МГц поддерживает максимальную скорость передачи символов RS=2W=310⁶ символ/с (см. уравнение (3.80)). Следовательно, каждый импульс, модулированный РАМ, должен иметь l-битовое значение.

Откуда

.

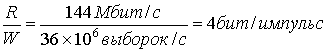где l = log2 L, a L=16 уровней.