Пропускная способность двоичного дискретного канала связи определяется формулой (29). В настоящее время в двоичном канале связи скорость передачи символов v может достигать значения 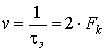. В связи с этим формула (29) может быть переписана в следующем виде:

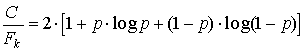. (50)

Для определённости будем считать, что в дискретном канале передача ведётся методом дискретной частотной модуляции, в этом случае вероятность ошибки определяется известной формулой

.

Подставив это выражение в формулу (50), получим зависимость пропускной способности дискретного двоичного канала связи от величины h (рис.14 - кривая 1). Из этого рисунка видно, что при h®¥ пропускная способность двоичного канала стремится к ( 2 × Fk × log2k).

Пропускная способность непрерывного канала связи определяется формулой Шеннона ( 41), откуда получаем

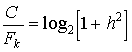. (51)

Эта зависимость также приведена также на рис. 14 (кривая 2).

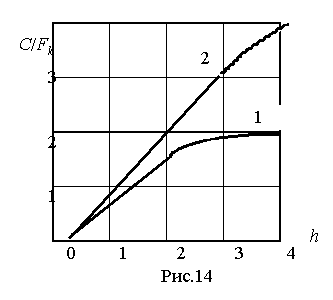
Сравнивая оба графика, видим, что при стремлении h к бесконечности для дискретного канала связи отношение C/Fk стремится к пределу (равному двум), а для непрерывного канала связи C/Fk неограниченно растёт, причём для любого значения h пропускная способность непрерывного канала связи превышает пропускную способность дискретного канала. Это объясняется тем, что сигналы дискретной модуляции отличаются от белого гауссовского шума, а согласно теореме Шеннона, наибольшей пропускной способностью обладают системы, в которых сигналы близки к белому гауссовскому шуму. Непрерывные сигналы по своей структуре ближе к гауссовскому шуму, чем дискретные сигналы.

Вопросы

1. Как изменяется пропускная способность дискретного канала связи при увеличении мощности сигнала?
2. Как изменяется пропускная способность непрерывного канала связи при увеличении мощности сигнала?
3. Почему пропускная способность непрерывного канала выше, чем пропускная способность дискретных каналов при любых значениях h > 0?