5.2. Классификация и основные характеристики метода сжатия данных
5.4.1. Алгоритмы полиноминальных методов сжатия
5.4.2. Экстраполяционные методы сжатия
5.4.3. Оптимальное линейное предсказание
5.1. Вводные замечания
В системе с циклической дискретизацией избыточность данных возникает даже при правильно выбранной частоте опроса датчиков, т.к. при мало меняющихся во времени параметрах частота опроса остается той же, что и на участках, где такая частота является необходимой. Т.о., целью сжатия данных является формирование минимального количества координат, обеспечивающих воспроизведение первичного сигнала с заданной вероятностью. Для пояснения вышесказанного рассмотрим изменение некоторой функции на интервале представления (рисунок 5.1).
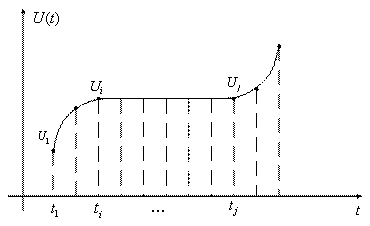
Рисунок 5.1
Передача дискретных значений 
на участке 
дает избыточную информацию о поведении функции 
. Передача избыточной информации приводит к расширению полосы частот в канале связи, увеличивает время необходимое для обработки информации и расход энергии источника питания.
Т.о., сжатие объема сообщений позволяет:
- Уменьшить требуемую пропускную способность канала передачи информации, а также объем памяти запоминающих устройств.
- Увеличить оперативность получения необходимой информации.
- Уменьшить требования к весу, объему, энергетическим показателям различных устройств РТМС.
Сократить избыточность информации можно в различных сечениях тракта РТМС (рисунок 5.2), где Д – датчики, УСИ – устройство сокращения информации, РТС – радиотехническая система, ЛС – линия связи, УОИ – устройство обработки информации.
Рисунок 5.2
Сжимать информацию можно:
- На выходе Д путем предварительной обработки информации, например, с помощью адаптивной коммутации.
- На выходе РТМС с целью разгрузки системы передачи информации, например, путем рационального кодирования и используя необратимые методы сжатия.
- На входе устройств первичной обработки путем отбора наиболее важной информации.
5.2. Классификация и основные характеристики метода сжатия данных
Существует несколько методов сжатия объема сообщения (рисунок 5.3), где ИИД – исключение избыточных данных, АД – адаптивная дискретизация, АК – адаптивная коммутация, АРЧ – автоматическая регулировка частоты опроса сигнала.
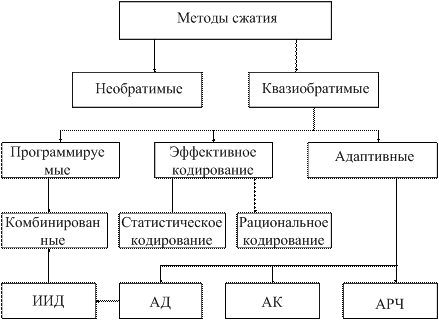
Рисунок 5.3
По возможности восстановления исходного сигнала все методы сжатия делятся на необратимые и квазиобратимые. К необратимым относятся методы, при которых на приемную сторону передается не сам сигнал как функция времени, а какие-то его характеристики. Имея эти характеристики невозможно восстановить исходный сигнал как функцию времени. В качестве таких характеристик могут выступать спектральная плотность мощности, функция плотности вероятности, форма корреляционной функции. К квазиобратимым относятся методы допускающие восстановление исходного сигнала с определенной степенью верности.
Программируемые представления предполагают возможность изменения способа представления или его показателей, например частоты опроса, в ходе работы системы. Смена режима производится или по решению оператора или по определенной программе. Число различных основных показателей такого представления обычно ограничено.
К методам сжатия данных путем эффективного кодирования относятся методы представления измеряемой информации в дискретной форме, требующие минимального количества символов при заданных показателях верности. К эффективному кодированию относится статистическое и рациональное кодирование. Алгоритмы статистического кодирования позволяют сократить число двоичных символов в коде при передаче отдельных фрагментов сообщений с большой вероятностью появления. Например, гласные имеют большую вероятность появления, поэтому их можно кодировать кодом с минимальным количеством символов и наоборот. Алгоритмы рационального кодирования обеспечивают передачу сообщений с минимальным количеством символов при том же качестве восстановления сигналов в условиях априорной неопределенности относительно вероятностных и спектральных характеристик.
Адаптивные методы сжатия данных позволяют уменьшить среднюю частоту дискретизации. Они основаны на кусочной аппроксимации измеряемой величины более простой функцией времени и передаче дискретных значений измеряемой величины при достижении погрешностью аппроксимации некоторого заданного значения. Для реализации адаптивных методов могут применяться адаптивная коммутация каналов, адаптивная дискретизация и исключение избыточных данных. Возможно применение комбинированного метода, сочетающего в себе принципы программируемых систем и систем, исключающих избыточные данные. В некотором случае целесообразно применять РТМС с автоматическим регулированием частоты опроса датчиков. Адаптивные методы делятся на одно- и двухпараметрические. В случае однопараметрической адаптации может фиксироваться длительность интервала сообщения и тогда изменяется число формируемых координат или может фиксироваться число формируемых координат и тогда изменяется длительность интервала сообщения. При двухпараметрической адаптации изменяется число формируемых координат и длительность сообщений. РТМС со сжатием данных характеризуется рядом коэффициентов:
1. Коэффициент сжатия данных - определяется как отношение 
отсчета измеряемой величины, передаваемой без сжатия, к количеству отсчетов 
в системе со сжатием, за продолжительность времени 
при заданной верности :
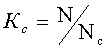. (5.1)
Существует информационная трактовка этого коэффициента:
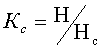, (5.2)
где 
- количество передаваемой информации в системе без сжатия, 
- среднее количество передаваемой информации в системе со сжатием.
2. Коэффициент эффективности, позволяющий получить сравнительную оценку различных методов сжатия.
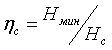, (5.3)
где 
- минимальное количество информации, которое при заданном ограничении, например, длительности интервала представления, необходимо передавать в системе. Коэффициент эффективности является абсолютной характеристикой способа представления сообщения в данном классе.
3. Коэффициент помехоустойчивости, характеризующий чувствительность сообщения к искажению координат
(5.4)
где 
- значения показателя верности в системе без сжатия и со сжатием данных. Помехоустойчивость системы может характеризоваться коэффициентами сжатия по полосе и мощности.
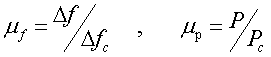, (5.5)
где 
- полоса частот и мощность источника питания на передающей стороне в системе без сжатия и со сжатием данных, обеспечивающие ту же верность.
4. Время задержки сообщения в аппаратуре сжатия - 
. На этот параметр накладываются ограничения, определяемые временем протекания аварийных процессов, т.к. в этом случае вся накопленная в оперативной памяти информация может быть потеряна.
5. Коэффициент сложности алгоритма - характеризует среднее число вычисляемых операций или команд, реализуемых аппаратурой сжатия данных для вычисления одной координаты.
5.3. Программируемые РТМС
В рассматриваемых РТМС сокращение избыточности достигается за счет установления на некотором отрезке времени для каждого параметра или группы параметров своей частоты опроса. Установка частоты опроса 
осуществляется по известным максимальным характеристикам параметров: граничной частоты спектра, минимальным интервалом корреляции и максимальной скорости изменения параметра. Для программного изменения частоты опроса должны быть известны указанные априорные сведения. На рисунке 5.4 показано, что на интервалах 
частота опроса меняется дискретно.
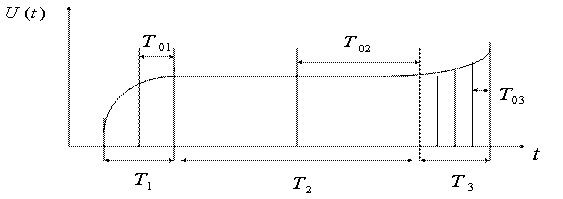
Рисунок 5.4
Скачкообразное изменение частоты опроса позволяет сократить избыточность, сохраняя заданное значение погрешности дискретизации.
Структурная схема передающей части программируемой РТМС представлена на рисунке 5.5, где Д – датчики, К – коммутатор, РПУ – радиопередающее устройство, УУ+ЗУ – устройство управления и запоминающее устройство.
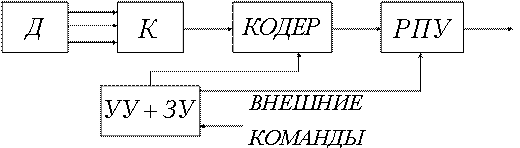
Рисунок 5.5
Управляющие сигналы поступают на вход коммутатора, кодирующего устройства и передатчика, изменяя их характеристики. Программа управления хранится в ЗУ и обновляется по внешним командам.
Недостатки программируемых РТМС:
- Необходимость наличия априорных сведений об измеряемых параметрах.
- Дискретное изменение частоты опроса, ведущее к некоторой избыточности.
Достоинства программируемых РТМС:
- Простота реализации и высокая информационная гибкость.
- Сокращение объема передаваемых данных за счет сокращения избыточности по множеству параметров.
5.4. Адаптивные методы сжатия
5.4.1. Алгоритмы полиноминальных методов сжатия
На основе полиноминальных методов сжатия данных разработаны алгоритмы адаптивной дискретизации и исключения избыточности данных. В отличие от методов регулярных выборок при использовании полиноминальных методов сжатия точка опроса не образует периодической последовательности. В этом случае передаются и запоминаются существенные выборки (рисунок 5.6).
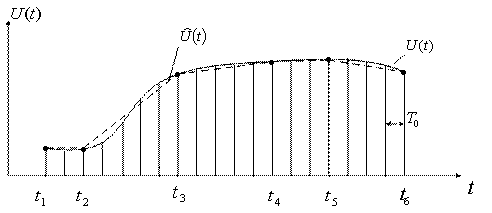
Рисунок 5.6
Под существенными выборками понимаются выборки, позволяющие получать на приемной стороне первичный сигнал 
с заданной точностью. Т.к. существенные выборки не образуют регулярную последовательность, то для получения оценки первичного сигнала необходимо передавать дополнительную информацию в виде значений времени … появления существенных выборок. Для формирования существенных выборок обычно используется кусочная аппроксимация измеряемых величин алгебраическим полиномом.
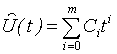, (5.6)
где 
- коэффициенты полинома.
Для реализации полиноминальных методов сжатия необходимо устройство, определяющее погрешность аппроксимации и изменяющее режим работы системы, т.е. частоту опроса. В зависимости от типа преобразователей погрешности аппроксимации известны экстраполяционные и интерполяционные алгоритмы адаптивного сжатия.
5.4.2. Экстраполяционные методы сжатия
Сущность метода экстраполяции, т.е. предсказания, заключается в получении упрежденных значений параметра на основе предшествующих данных. Если текущее значение параметра отличается от предшествующего не больше, чем на величину заданного допуска, то оно отбрасывается. Для предсказания (
)-го отсчета, если известны 
предыдущих отсчетов используется формула:
. 
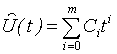(5.7)
В зависимости от степени полинома различают предсказатели нулевого, первого и т.д. порядка. Рассмотрим предсказатель нулевого порядка (рисунок 5.7). В этом случае степень полинома 
, а предсказанное значение 
. Таким образом, если имеется отсчет 
, то предполагается, что последующие отсчеты 
и т.д. равны .
Относительно величины отсчета устанавливается зона 
. Эта зона называется зоной сравнения или апертурой. Для каждого 
-го отсчета, следующего за 
-ым существенным отсчетом, вычисляется разность:
. (5.8)
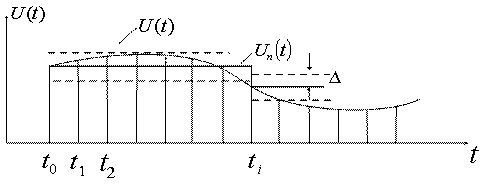
Рисунок 5.7
Отсчет считается существенным, если 
. Сжатие с помощью полинома нулевого порядка требует запоминание последнего существенного отсчета. Блок - схема алгоритма данного метода показана на рисунке 5.8.
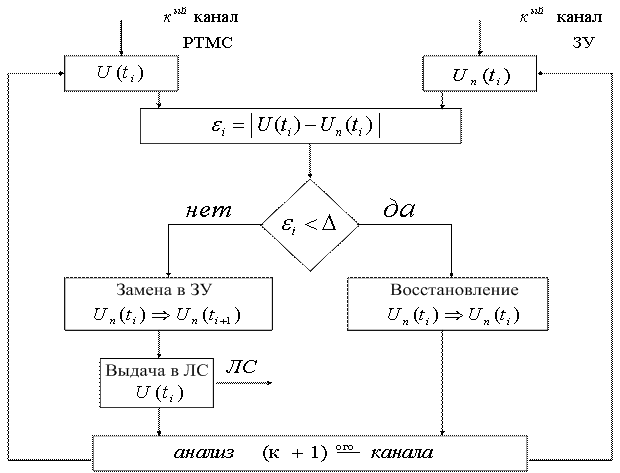
Рисунок 5.8
Рассмотрим теперь предсказатель первого порядка. Степень полинома в этом случае m=1. Для построения полинома требуется два предшествующих отсчета, через которые проводится прямая линия. Предсказанное значение для последующих отсчетов лежит на этой линии (рисунок 5.9).
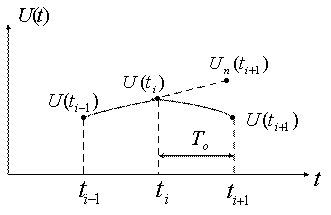
Рисунок 5.9
Предсказанное для момента времени 
значение параметра рассчитывается по формуле:
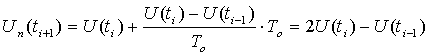. (5.9)
Если ошибка 
, то отсчет исключается. В этом случае для расчета предсказанного значения в точке 
используется формула:
. (5.10)
Сжатие с помощью предсказателя первого порядка требует запоминание последнего существенного отсчета и предсказанного значения отсчета (рисунок 5.10).
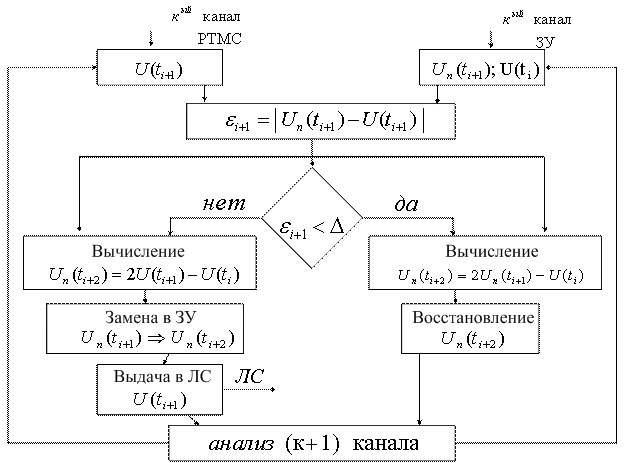
Рисунок 5.10
Согласно экспериментальным данным при сжатии медленно меняющихся параметров предсказатель нулевого порядка дает коэффициент сжатия около 50, а предсказатель первого порядка – 70. Использование полиномов более высокого порядка даёт небольшое приращение коэффициента сжатие, но приводит к увеличению вычислений и усложнению экстраполятора. Наиболее помехоустойчивы экстраполяторы низких порядков, поэтому обычно используются экстраполяторы нулевого и первого порядка.
5.4.3. Оптимальное линейное предсказание
Для определения алгоритма оптимального линейного предсказания необходимо знать корреляционную функцию или энергетический спектр параметра. Значения параметра в момент времени 
предсказывается путем вычисления линейной комбинации предшествующих отсчетов по формуле:
, (5.11)
где коэффициенты 
выбираются из условия минимальной дисперсии разности предсказанного значения от действительной величины.
. (5.12)
Коэффициенты находятся путем решения системы уравнений вида:
, 
(5.13)
В случае если используется одно предшествующее значение параметра , то
, 
, (5.14)
где 
- коэффициент корреляции параметра, 
- период опроса.
Если используется два предшествующих значения параметра :
, 
(5.15)
Алгоритм работы при оптимального линейного предсказания строится также, как и при предсказании нулевого и первого порядка, но вычисление предсказания параметра осуществляется в соответствии с формулами (5.14) и (5.15).
Можно показать, что дисперсия отклонения предсказанного значения от действительного в случае предсказания нулевого порядка:
, (5.16)
а в случае предсказания первого порядка:
. (5.17)
5.4.4. Интерполяционные методы сжатия
Предсказание эффективно в том случае, если параметр плавно изменяется по времени. Если параметр искажается шумом или имеет быстрое изменение, то эффективность методов сжатия, основанных на предсказаниях, существенно снижается. В этом случае использование интерполяционных методов сжатия позволяет исключить большее число избыточных отсчетов. Сущность методов интерполяции состоит в замене параметров аппроксимирующей функцией вида:
(5.18)
Обычно в качестве таких функций используются полиномы нулевого и первого порядков.
Применение полиномов более высокого порядка приводит к резкому увеличению объема вычислений и не дает значительного приращения коэффициента сжатия.
Рассмотрим интерполяцию нулевого порядка. При этом 
и аппроксимирующей функцией является прямая линия параллельная оси абсцисс.
На отрезке интерполяции 
находится минимальное 
и максимальное 
значение параметров. Интерполяционная прямая равна:
(5.19)
Рассмотрим особенности в случае применения интерполяционного и экстраполяционного методов сжатия данных (рисунок 5.11).
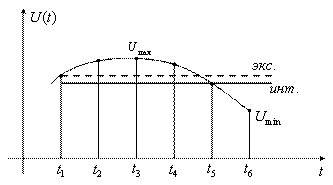
Рисунок 5.11
Для определения величины интерполяционного интервала произведем вычисление погрешности интерполяции
(5.20)
для все увеличивающегося интервала наблюдения.
Как только 
, то полученный интервал фиксируется. Обычно при экстраполяции ошибка аппроксимации параметра получается больше 
, а 
. Это объясняется тем, что при интерполяции значение существенного отсчета вычисляется в конце интервала интерполяции, т.е., с учетом не только предшествующего, но и последующего отсчетов. При экстраполяции существенным является первый отсчет. Но при интерполяции необходимо произвести больший объем вычислений, чем при экстраполяции. При интерполяции первого порядка в качестве интерполирующей функции используется прямая, которая может иметь произвольный наклон.
5.4.5. Сравнение полиномиальных методов сжатия
Основными факторами, определяющими применимость того или иного метода сжатия являются:
- эффективность изменения избыточности;
- сложность реализации алгоритмов сжатия данных.
Величина коэффициента сжатия зависит от алгоритма и определяется шириной апертуры, которая задает точность восстановления, а также характером изменения параметра. Последняя причина является очень существенной. При одной и той же апертуре в зависимости от характера изменения параметра коэффициент сжатия изменяется от десятков до сотен. Для ориентировочных расчетов можно использовать данные о коэффициенте сжатия, полученные при испытаниях ракеты “Поларис”.
На рисунке 5.12 представлены зависимости коэффициента сжатия от величины апертуры для трех алгоритмов.
ИПП – интерполятор первого порядка
ИНП – интерполятор нулевого порядка
ПНП – предсказатель нулевого порядка
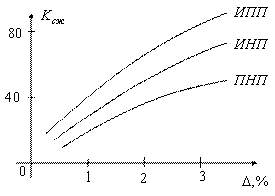
Рисунок 5.12
При использовании алгоритмов сжатия можно передавать данные, занимающие полосу 80 кГц в реальном масштабе времени в полосе телефонного канала 3,2 кГц.
При осуществлении сжатия возможно комбинированное использование нескольких алгоритмов, например, путем экстраполяции или интерполяции нулевого или первого порядка. Для одних участков изменения параметра большей эффективностью будет обладать первый алгоритм, а для других – второй.
Для сравнения рассмотрим следующие классы алгоритмов квазиобратимого сжатия.
1 – ПНП (предсказатель нулевого порядка);
2 – ППП (предсказатель первого порядка);
3 – ИНП (интерполятор нулевого порядка);
4 – ИПП (интерполятор первого порядка);
5 – ПНП-ИПП (комбинированный алгоритм)
6 – комбинированный алгоритм ИНП-ИПП.
Для удобства анализа критерии качества исследуемых алгоритмов относились к соответствующим значениям алгоритма ПНП.
Сложность аппаратурной реализации оценивалась количеством интегральных микросхем (МК), необходимых для построения устройства, или количеством элементарных операций (ОП) на обработку одного отсчета, или объемом оперативной памяти запоминающего устройства (ЗУ), требуемый для обработки одного параметра (рисунок 5.13).
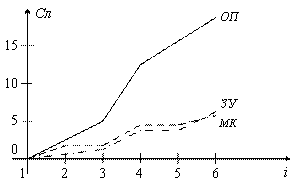
Рисунок 5.13
Получены значения коэффициента сжатия данных, полученные при анализе данных поступающих с космического аппарата Луна-15 (рисунок 5.14).
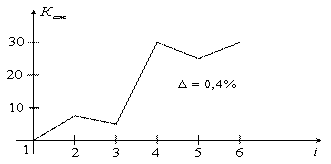
Рисунок 5.14
Для алгоритмов 1, 2, 3 коэффициент сжатия пропорционален сложности реализации. Причем, сложность интерполятора (алгоритм 3) выше, чем у алгоритма 1. Алгоритм 4 (ИПП) обеспечивает коэффициент сжатия примерно 30, а затраты реализации в 4 раза превышают затраты на построение алгоритма 1. Наиболее простая техническая реализация у алгоритма ППП и алгоритма ИПП, когда гладкие процессы, и алгоритма ИПП, когда шумовые процессы.
Полиномиальные методы сжатия данных реализуются в конкретных адаптивных системах.