Если известна передаточная функция дискретного фильтра, то для реализации фильтра с конечной импульсной характеристикой , равной нулю везде кроме , поступают следующим образом. Амплитудно-частотную характеристику фильтра дискретизируют, разбивая частотный интервал W = 0 ¸ 1 на N равных интервалов. В результате получают последовательность отсчетов АЧХ на N частотах , т.е. , . Поскольку , то, подставляя эту последовательность в формулу обратного дискретного преобразования Фурье (10), получаем выражение для дискретной импульсной характеристики фильтра

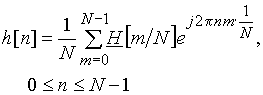(34)

Как известно, конечную импульсную характеристику имеют нерекурсивные фильтры. Это значит, что полученные отсчеты дискретной импульсной характеристики являются коэффициентами усиления , , ..., в схеме нерекурсивного фильтра, приведенной на рис. 40, а.

Пример 24.1. Найдем импульсную характеристику фильтра нижних частот, имеющего граничную частоту полосы пропускания W = 0,1, и АЧХ, приведенную на рис. 61. Импульсную характеристику будем рассчитывать для значения N = 30.

В формуле (34) для расчета используются комплексные значения передаточной функции. Если выбрать значения , показанные на рис. 61 ( = 1 в полосе пропускания и = 0 в полосе непропускания) и фазу передаточной функции , равную нулю, то передаточная функция будет иметь заданные значения в точках , но очень сильно отличаться от требуемой формы на частотах W между этими точками.

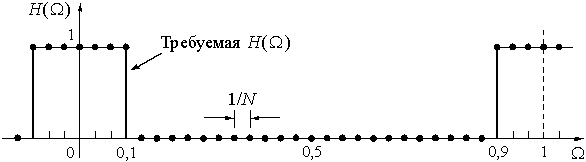
Рис. 61

Гораздо лучшие результаты получаются, если выбрать . Выбор такой фазы эквивалентен тому, что вместо 1 в полосе пропускания. Такой передаточной функции соответствует АЧХ, изображенная на рис. 62. Подстановка значений в формулу (34) позволяет получить выражение для расчета :

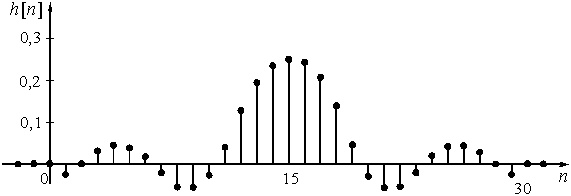
Рис. 63

.

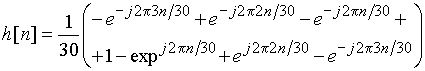График конечной импульсной характеристики изображен на рис. 63.

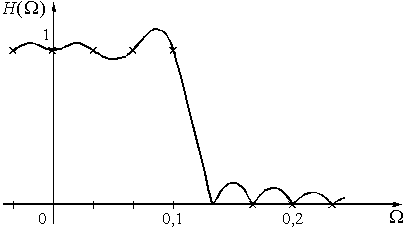
Рис. 62

Для реализации фильтра с такой импульсной характеристикой по схеме рис. 40, а потребуется 30 усилителей и 29 элементов задержки, т.е. схема довольно громоздкая. Схема с обратными связями, реализующая АЧХ, изображенную на рис. 61, будет иметь гораздо меньше элементов. Однако достоинством нерекурсивных фильтров с конечной импульсной характеристикой является то, что они всегда устойчивы и, кроме того, обеспечивают линейные фазовые характеристики.

Самоконтроль

1. Каков алгоритм реализации фильтра с конечной импульсной характеристикой?

2. Как перейти от передаточной функции к дискретной импульсной характеристике фильтра?

3. Какой вид имеет структурная схема фильтра с конечной импульсной характеристикой?