5.1. Прием сигналов как статистическая задача
5.2. Критерии оптимального приема сигналов
5.3. Оптимальный прием дискретных сигналов
5.4. Вероятность ошибки при когерентном приеме двоичных сигналов
5.5. Вероятность ошибки при когерентном приеме многопозиционных сигналов
5.6. Некогерентный прием дискретных сигналов
5.7. Передача дискретных сигналов по каналам с переменными параметрами
5.1. Прием сигналов как статистическая задача
Обычно способ передачи (способ кодирования и модуляции) задан и нужно определить помехоустойчивость, которую обеспечивают различные способы приема. Какой из возможных способов приема является оптимальным? Указанные вопросы являются предметом рассмотрения теории помехоустойчивости, основы; которой разработаны академиком В. А. Котельниковым.
Помехоустойчивостью системы связи называется способность системы различать (восстанавливать) сигналы с заданной достоверностью.
Задача определения помехоустойчивости всей системы в целом весьма сложная. Поэтому часто определяют помехоустойчивость отдельных звеньев системы: приемника при заданном способе передачи, системы кодирования или системы модуляции при заданном способе приема и т. д.
Предельно достижимая помехоустойчивость называется, по Котельникову, потенциальной помехоустойчивостью. Сравнение потенциальной и реальной помехоустойчивости устройства позволяет дать оценку качества реального устройства и найти еще неиспользованные резервы. Зная, например, потенциальную помехоустойчивость приемника, можно судить, насколько близка к ней реальная помехоустойчивость существующих способов приема и насколько целесообразно их дальнейшее усовершенствование при заданном способе передачи.
Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнить эти способы передачи между собой и указать, какие из них в этом отношении являются наиболее совершенными.
При отсутствии помех каждому принятому сигналу х соответствует вполне определенный сигнал s. При наличии помех это однозначное соответствие нарушается. Помеха, воздействуя на передаваемый сигнал, вносит неопределенность относительно того, какое из возможных сообщений было передано, и по принятому сигналу х только с некоторой вероятностью можно судить о том, что был передан тот или иной сигнал s. Эта неопределенность описывается апостериорным распределением вероятностей P(s/x).
Если известны статистические свойства сигнала s и помехи w, то можно создать приемник, который на основании анализа сигнала х будет находить апостериорное распределение P(s/x). Затем по виду этого распределения принимается решение о том, какое из возможных сообщений было передано. Решение принимается оператором или самим приемником по правилу, которое определяется заданным критерием.
Задача состоит в том, чтобы воспроизвести передаваемое сообщение наилучшим образом в смысле выбранного критерия. Такой приемник называется оптимальным, а его помехоустойчивость будет максимальной при заданном способе передачи.
Несмотря на случайный характер сигналов х, в большинстве случаев имеется возможность выделить множество наиболее вероятных сигналов ![]() соответствующих передаче некоторого сигнала st. Геометрическое представление позволяет множество сигналов заменить областью многомерного пространства.
соответствующих передаче некоторого сигнала st. Геометрическое представление позволяет множество сигналов заменить областью многомерного пространства.
Пусть область X принимаемых сигналов разбита на неперекрывающиеся области ![]() причем каждому сигналу s
причем каждому сигналу s![]() соответствует область Х
соответствует область Х![]() . Если принятый сигнал попал в эту область, то приемник принимает решение о том, что передавался сигнал s
. Если принятый сигнал попал в эту область, то приемник принимает решение о том, что передавался сигнал s![]() С некоторой вероятностью сигнал Xi может попасть в любую другую область
С некоторой вероятностью сигнал Xi может попасть в любую другую область ![]() , и тогда принимается ошибочное решение: вместо сигнала s
, и тогда принимается ошибочное решение: вместо сигнала s![]() , воспроизводится сигнал
, воспроизводится сигнал ![]() . Вероятность того, что переданный сигнал принят правильно, равна
. Вероятность того, что переданный сигнал принят правильно, равна ![]() , а вероятность того, что он принят ошибочно, равна
, а вероятность того, что он принят ошибочно, равна ![]() . Условная вероятность
. Условная вероятность ![]() ) зависит от способа формирования сигнала, от помех, имеющихся в канале, и от выбранной решающей схемы приемника. Полная вероятность ошибочного приема элемента сигнала, очевидно, будет равна:
) зависит от способа формирования сигнала, от помех, имеющихся в канале, и от выбранной решающей схемы приемника. Полная вероятность ошибочного приема элемента сигнала, очевидно, будет равна:
![]() (5.1)
(5.1)
где ![]() — априорные вероятности передаваемых сигналов.
— априорные вероятности передаваемых сигналов.
В случае двоичного канала область принимаемых сигналов разбивается на две области X![]() и Xz. Если сигнал х попадает в область X
и Xz. Если сигнал х попадает в область X![]() , то воспроизводится сигнал
, то воспроизводится сигнал![]() , а если в область X
, а если в область X![]() , то — s2.
, то — s2.
В канале последовательность элементов входного сообщения u(t) преобразовывается в последовательность элементов выходного сообщения v(t). В геометрическом представлении это означает преобразование пространства входных сообщений U в пространство выходных сообщений V. При изучении каналов иногда удобно рассматривать вместо элементов исходного сообщения последовательность кодовых символов.
Канал называется дискретным, если входные и выходные пространства (сообщения) дискретны, и непрерывным, если эти пространства непрерывны. Если одно из пространств дискретно, а другое — непрерывно, то канал называется соответственно дискретно-непрерывным или непрерывно-дискретным.
Свойства дискретного канала определены, если заданы: алфавиты входных кодовых символов ![]() и выходных
и выходных ![]() , скорость передачи символов V и вероятности переходов
, скорость передачи символов V и вероятности переходов ![]() т. е. вероятности того, что принят символ
т. е. вероятности того, что принят символ ![]() , когда был передан символ
, когда был передан символ ![]() ,-. В общем случае
,-. В общем случае ![]() и символы
и символы ![]() могут отличаться по своей природе от символов
могут отличаться по своей природе от символов ![]() , . Например, звуки речи, составляющие входной алфавит при телефонной передаче, могут воспроизводиться на приемном конце не только в виде звука, но и в виде текста, записанного на пленку.
, . Например, звуки речи, составляющие входной алфавит при телефонной передаче, могут воспроизводиться на приемном конце не только в виде звука, но и в виде текста, записанного на пленку.
Если вероятности переходов Р(![]() /
/![]() ) для каждой пары i, j не зависят от времени и от того, какие символы передавались и принимались ранее, то такой канал называется однородным без памяти. Если эти вероятности зависят от времени, то канал называется неоднородным, а если они зависят от того, какие символы передавались и принимались ранее, то канал называется каналом с памятью. Математическим описанием канала с памятью является дискретная цепь Маркова.
) для каждой пары i, j не зависят от времени и от того, какие символы передавались и принимались ранее, то такой канал называется однородным без памяти. Если эти вероятности зависят от времени, то канал называется неоднородным, а если они зависят от того, какие символы передавались и принимались ранее, то канал называется каналом с памятью. Математическим описанием канала с памятью является дискретная цепь Маркова.
Если в однородном канале алфавиты кодовых символов на входе и выходе одинаковы и для любой пары ![]() вероятности переходов постоянны
вероятности переходов постоянны ![]() , то такой канал называется симметричным (рис. 5.1а).
, то такой канал называется симметричным (рис. 5.1а).
Среди каналов, в которых алфавиты на входе и выходе неодинаковы, представляет интерес так называемый стирающий канал,
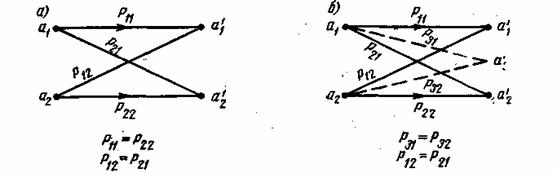
Рис. 5.1. Графическое представление работы однородного бинарного канала: симметричный канал (а), канал со стиранием (б)
в котором ![]() . В таком канале выходной алфавит содержит дополнительный символ
. В таком канале выходной алфавит содержит дополнительный символ ![]() обозначающий «стирание». Появление этого символа на выходе означает, что переданный символ искажен помехами и не может быть опознан. Как будет показано в дальнейшем, введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации. Геометрическое представление стирающего канала дано на рис. 5.16. В канале без помех каждому входному символу
обозначающий «стирание». Появление этого символа на выходе означает, что переданный символ искажен помехами и не может быть опознан. Как будет показано в дальнейшем, введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации. Геометрическое представление стирающего канала дано на рис. 5.16. В канале без помех каждому входному символу ![]() однозначно соответствует символ a'k на выходе (вероятности неправильных переходов равны нулю).
однозначно соответствует символ a'k на выходе (вероятности неправильных переходов равны нулю).
5.2. Критерии оптимального приема сигналов
Для того чтобы определить, какая из решающих схем является оптимальной, необходимо прежде всего установить, в каком смысле понимается оптимальность. Выбор критерия оптимальности не является универсальным, он зависит от поставленной задачи и условий работы системы.
Пусть на вход приемника поступает сумма сигнала и помехи ![]() , где S
, где S![]() (t) — сигнал, которому соответствует кодовый символ ak,
(t) — сигнал, которому соответствует кодовый символ ak, ![]() — аддитивная помеха с известным законом распределения. Сигнал
— аддитивная помеха с известным законом распределения. Сигнал![]() . в месте приема является случайным с априорным распределением P(S
. в месте приема является случайным с априорным распределением P(S![]() ). На основании анализа колебания x(t) приемник воспроизводит сигнал
). На основании анализа колебания x(t) приемник воспроизводит сигнал ![]() . При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение,
. При наличии помех это воспроизведение не может быть совершенно точным. По принятой реализации сигнала приемник вычисляет апостериорное распределение,![]() содержащее все сведения, которые можно извлечь из принятой реализации сигнала x(t). Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения
содержащее все сведения, которые можно извлечь из принятой реализации сигнала x(t). Теперь необходимо установить критерий, по которому приемник будет выдавать на основе апостериорного распределения ![]() решение относительно переданного сигнала
решение относительно переданного сигнала ![]() .
.
При передаче дискретных сообщений широко используется критерий Котельникова (критерий идеального наблюдателя). Согласно этому критерию принимается решение, что передан сигнал ![]() , для которого апостериорная вероятность
, для которого апостериорная вероятность ![]() имеет наибольшее значение, т. е. регистрируется сигнал
имеет наибольшее значение, т. е. регистрируется сигнал ![]() если выполняются неравенства
если выполняются неравенства
![]() (5.2)
(5.2)
При использовании такого критерия полная вероятность ошибочного решения будет минимальной. Действительно, если по сигналу х принимается решение о том, что был передан сигнал ![]() ,-, то, очевидно, вероятность правильного решения будет равна
,-, то, очевидно, вероятность правильного решения будет равна ![]() , а вероятность ошибки
, а вероятность ошибки ![]() —Отсюда следует, что максимуму апостериорной вероятности
—Отсюда следует, что максимуму апостериорной вероятности ![]() соответствует минимум пол ной вероятности ошибки (5.1).
соответствует минимум пол ной вероятности ошибки (5.1).
На основании формулы Байеса (2.26)
![]() (5.3)
(5.3)
Тогда неравенство (5.2) можно записать в другом виде
![]() (5.4)
(5.4)
или
![]() (5.5)
(5.5)
Функцию p(x/s) часто называют функцией правдоподобия. Чем больше значение этой функции при данной реализации сигнала x, тем правдоподобнее, что передавался сигнал s. Отношение, входящее в неравенство (5.5)
![]() (5.6)
(5.6)
называется отношением правдоподобия. Пользуясь этим понятием, правило решения (5.5), соответствующее критерию Котельникова, можно записать в виде
![]() (5.7)
(5.7)
Если передаваемые сигналы равновероятны ![]() , то это правило решения принимает более простой вид
, то это правило решения принимает более простой вид
![]() (5.8)
(5.8)
Таким образом, критерий идеального наблюдателя сводится к сравнению отношений правдоподобия (5.7). Этот критерий является более общим и называется критерием максимального правдоподобия.
Рассмотрим бинарную систему, в которой передача сообщений осуществляется с помощью двух сигналов ![]() и
и ![]() , соответствующих двум кодовым символам а
, соответствующих двум кодовым символам а![]() и a
и a![]() . Решение принимается по результату обработки принятого колебания x(t) пороговым методом: регистрируется s
. Решение принимается по результату обработки принятого колебания x(t) пороговым методом: регистрируется s![]() если х<х0, и s2, если
если х<х0, и s2, если ![]() , где х0— некоторый пороговый уровень х. Здесь могут быть ошибки двух видов: воспроизводится s
, где х0— некоторый пороговый уровень х. Здесь могут быть ошибки двух видов: воспроизводится s![]() , когда передавался
, когда передавался ![]() и
и ![]() ,когда передавался s
,когда передавался s![]() . Условные вероятности этих ошибок (вероятности переходов) будут равны:
. Условные вероятности этих ошибок (вероятности переходов) будут равны:
![]() (5.9)
(5.9)
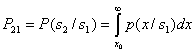 (5.10)
(5.10)
Значения этих интегралов могут быть вычислены как соответствующие площади, ограниченные графиком плотностей условного распределения вероятностей (рис. 5.2). Вероятности ошибок первого и второго вида соответственно:
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
Полная вероятность ошибки при этом
![]() (5.13)
(5.13)
Пусть p![]() =p
=p![]() , тогда
, тогда
![]()
Нетрудно убедиться, что в этом случае минимум Р0имеет место. При ![]() , т. е. при выборе порога в соответствии с рис. 5.2.
, т. е. при выборе порога в соответствии с рис. 5.2.
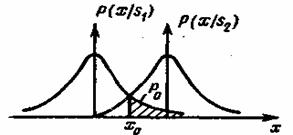
Рис. 5.2. График плотности условного распределения вероятностей при передаче сигналов st и s2
Для такого порога ![]() . На рис. 5.2 значение
. На рис. 5.2 значение ![]() определяется заштрихованной площадью. При любом другом значении порога величина
определяется заштрихованной площадью. При любом другом значении порога величина ![]() будет больше.
будет больше.
Несмотря на естественность и простоту, критерий Котельникова имеет недостатки. Первый заключается в том, что для построения решающей схемы, как это следует из соотношения (5.4), не-
обходимо знать априорные вероятности передачи различных символов кода. Вторым недостатком этого критерия является то, что все ошибки считаются одинаково нежелательными (имеют одинаковый вес). В некоторых случаях такое допущение не является правильным. Например, при передаче чисел ошибка в первых значащих цифрах более опасна, чем ошибка в последних цифрах. Пропуск команды или ложная тревога в различных системах оповещения могут иметь различные последствия.
Следовательно, в общем случае при выборе критерия оптимального приема необходимо учитывать те потери, которые несет получатель сообщения при различных видах ошибок. Эти потери можно выразить некоторыми весовыми коэффициентами, приписываемыми каждому из ошибочных решений. Обозначим потери ошибочных решений первого и второго видов соответственно ![]() и l
и l![]() . Тогда можно определить средние ожидаемые потери или средний риск
. Тогда можно определить средние ожидаемые потери или средний риск
![]() (5.14)
(5.14)
Оптимальной решающей .схемой будет такая, которая обеспечивает минимум среднего риска. Критерий минимального риска относится к классу так называемых байесовых критериев.
В радиолокации широко используется критерий Неймана — Пирсона. При выборе этого критерия учитывается, во-первых, что ложная тревога и пропуск цели не являются равноценными по своим последствиям, и, во-вторых, что неизвестна априорная вероятность передаваемого сигнала. Если пропуск цели является более нежелательным, то можно задать некоторую величину ![]() допустимой вероятности ложной тревоги и потребовать, чтобы решающая схема максимизировала вероятность правильного обнаружения Р
допустимой вероятности ложной тревоги и потребовать, чтобы решающая схема максимизировала вероятность правильного обнаружения Р![]() (или, что то же, минимизировать вероятность пропуска Р
(или, что то же, минимизировать вероятность пропуска Р![]() ).
).
Согласно критерию Неймана—Пирсона приемник является оптимальным в том случае, если при заданной вероятности ложной тревоги
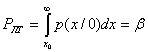 (5.15)
(5.15)
он обеспечивает наибольшую вероятность правильного обнаружения
![]() (5.16)
(5.16)
Можно показать, что критерий Неймана—Пирсона приводит к следующему правилу решения: цель считается обнаруженной, если
![]() (5.17)
(5.17)
где ![]() — некоторое число, определяемое допустимой вероятностью ложной тревоги
— некоторое число, определяемое допустимой вероятностью ложной тревоги ![]()
5.3. Оптимальньй прием дискретных сигналов
Источник дискретных сообщений характеризуется совокупностью возможных элементов сообщения ![]() и вероятностями появления этих элементов на выходе источника
и вероятностями появления этих элементов на выходе источника ![]() . В передающем устройстве сообщение преобразовывается в сигнал таким образом, что каждому элементу сообщения соответствует определенный сигнал. Обозначим эти сигналы через
. В передающем устройстве сообщение преобразовывается в сигнал таким образом, что каждому элементу сообщения соответствует определенный сигнал. Обозначим эти сигналы через ![]() , a их вероятности появления на выходе передатчиков (априорные вероятности) соответственно через
, a их вероятности появления на выходе передатчиков (априорные вероятности) соответственно через ![]() . Очевидно, априорные вероятности сигналов P(s
. Очевидно, априорные вероятности сигналов P(s![]() ) равны априорным вероятностям P(u
) равны априорным вероятностям P(u![]() ) соответствующих сообщений
) соответствующих сообщений ![]() . В процессе передачи на сигнал накладывается помеха. Пусть эта помеха имеет равномерный спектр мощности с интенсивностью
. В процессе передачи на сигнал накладывается помеха. Пусть эта помеха имеет равномерный спектр мощности с интенсивностью ![]()
Тогда сигнал на входе можно представить как сумму переданного сигнала S![]() (t) и помехи w (t):
(t) и помехи w (t):
![]()
Поскольку сигналы ![]() x(t) и помеха
x(t) и помеха ![]() (t) заданы на конечном интервале (0<t<Т), то согласно (2.70) их можно представить в виде разложений по ортогональным функциям:
(t) заданы на конечном интервале (0<t<Т), то согласно (2.70) их можно представить в виде разложений по ортогональным функциям:
![]() (5.18)
(5.18)
![]() (5.19)
(5.19)
![]() (5.20)
(5.20)
где
![]() (5.21)
(5.21)
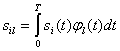 (5.22)
(5.22)
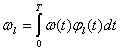 (5.23)
(5.23)
Так как мы предполагаем, что помеха имеет нормальное распределение, то и коэффициенты Фурье в выражении (5.23) будут иметь нормальное распределение с дисперсией ![]() и средним значением, равным нулю:
и средним значением, равным нулю:
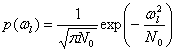 (5.24)
(5.24)
Коэффициенты x![]() также имеют нормальное распределение с той же дисперсией
также имеют нормальное распределение с той же дисперсией ![]() и средним значением
и средним значением ![]()
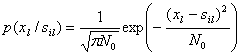 (5.25)
(5.25)
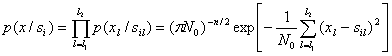 (5.26)
(5.26)
В силу независимости коэффициентов ![]() многомерное распределение коэффициентов х
многомерное распределение коэффициентов х![]() т. е. условное распределение p(x/s
т. е. условное распределение p(x/s![]() ), будет равно произведению одномерных распределений (5.25):
), будет равно произведению одномерных распределений (5.25):
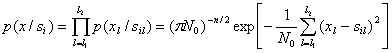 (5.26)
(5.26)
Подставляя это выражение в (5.5), получим следующее неравенство, определяющее условие оптимального приема по Котельникову:
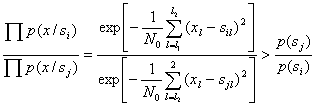 (5.27)
(5.27)
Логарифмируя обе части неравенства, приходим к эквивалентному выражению
![]() (5.28)
(5.28)
В соответствии с выражениями (5.20) и (5.18) имеем
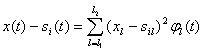 (5. 29)
(5. 29)
После возведения в квадрат и усреднения по времени выражения (5.29) с учетом свойств ортогональных функций ![]() (t) (2.55) получаем
(t) (2.55) получаем
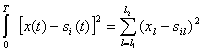 (5.30)
(5.30)
Тогда условие оптимального приема (5.28) можно записать в другом виде:
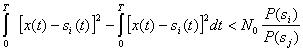 (5.31)
(5.31)
Неравенства (5.27) или им эквивалентные неравенства (5.28) и (5.31) определяют условия правильного приема сигнала s![]() (t). В случае, когда априорные вероятности сигналов одинаковы
(t). В случае, когда априорные вероятности сигналов одинаковы
![]() — , критерий Котельникова принимает более простой вид:
— , критерий Котельникова принимает более простой вид:
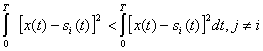 (5.32)
(5.32)
Отсюда следует, что при равновероятных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала.
Неравенство (5.32) можно записать в другом виде, раскрыв скобки:
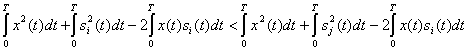
00
Для сигналов, энергии которых одинаковы, это неравенство для всех ![]() принимает более простую форму:
принимает более простую форму:
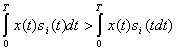 (5.33)
(5.33)
В этом случае условие оптимального приема можно сформулировать следующим образом. Если все возможные сигналы равновероятны и имеют одинаковую энергию, оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, взаимная корреляция которого с принятым сигналом максимальна.
Для двоичной системы полученным результатам можно дать весьма наглядную геометрическую трактовку. Пусть передаются два равновероятных сообщения и![]() и u2 с помощью сигналов
и u2 с помощью сигналов ![]() и s2. Первому сигналу соответствует вектор
и s2. Первому сигналу соответствует вектор ![]() в n-мерном пространстве, а второму — вектор s2. Принятому сигналу соответствует вектор х, равный сумме векторов сигнала s и помехи w. Пространство возможных значений сигнала можно разбить на две области так, чтобы при попадании конца вектора х в первую область воспроизводился сигнал
в n-мерном пространстве, а второму — вектор s2. Принятому сигналу соответствует вектор х, равный сумме векторов сигнала s и помехи w. Пространство возможных значений сигнала можно разбить на две области так, чтобы при попадании конца вектора х в первую область воспроизводился сигнал ![]() (область сигнала
(область сигнала![]() ) а при попадании в другую область — воспроизводился сигнал s2 (область сигнала s2). Если х, соответствующий данному сигналу, попадает в область другого сигнала, то происходит ошибка (вместо s\ воспроизводится s2 или, наоборот, s2 вместо s1). Вероятность ошибки, очевидно, зависит от конфигурации областей сигнала. В оптимальном приемнике Котельникова пространство сигналов разбивается на области сигнала si и сигнала s2 так, чтобы полная вероятность ошибки (5.13) была минимальной.
) а при попадании в другую область — воспроизводился сигнал s2 (область сигнала s2). Если х, соответствующий данному сигналу, попадает в область другого сигнала, то происходит ошибка (вместо s\ воспроизводится s2 или, наоборот, s2 вместо s1). Вероятность ошибки, очевидно, зависит от конфигурации областей сигнала. В оптимальном приемнике Котельникова пространство сигналов разбивается на области сигнала si и сигнала s2 так, чтобы полная вероятность ошибки (5.13) была минимальной.
В случае равновероятных сигналов и помехи с равномерным распределением оптимальным разбиением пространства будет такое, при котором любая точка х относится к области того сигнала s, конец вектора которого ближе всего к точке х. В двухмерной модели (рис. 5.3) для двоичной системы граница областей сигналов ![]() и s2 есть геометрическое место точек, равноотстоящих от
и s2 есть геометрическое место точек, равноотстоящих от ![]() и s2, т. е. гиперплоскость, перпендикулярная к вектору разности
и s2, т. е. гиперплоскость, перпендикулярная к вектору разности ![]() и делящая его пополам.
и делящая его пополам.
Если, например, передавался сигнал ![]() , то ошибка произойдет в том случае, когда выполняется неравенство
, то ошибка произойдет в том случае, когда выполняется неравенство
![]() (5.34)
(5.34)
Или
![]() (5.35)
(5.35)
где ![]() ,
, ![]() и
и ![]() — проекция w на вектор, коллинеарный
— проекция w на вектор, коллинеарный ![]() s, т. е.
s, т. е.
![]()
.Вместо неравенства (5.34) можно записать ![]() или в эвклидовой метрике
или в эвклидовой метрике
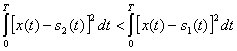 (5.36)
(5.36)
Условие (5.36) полностью совпадает с условием (5.32). Структурная схема приемника, реализующего операции (5.36), приведена на рис. 5.4. Здесь Г![]() и Г2 — генераторы опорных сигналов, формирующие точные копии переданных сигналов s1 и s2, В — вычитающее устройство, KB — квадратирующее устройство, И — интегратор, РУ — схема сравнения и выбора (решающее устройство).
и Г2 — генераторы опорных сигналов, формирующие точные копии переданных сигналов s1 и s2, В — вычитающее устройство, KB — квадратирующее устройство, И — интегратор, РУ — схема сравнения и выбора (решающее устройство).
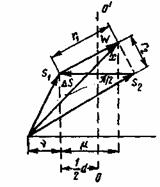
Рис. 5.3. Геометрическое представление работы оптимального приемника
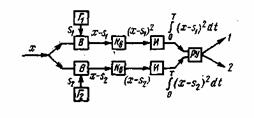
Рис. 5.4. Оптимальный приемник Котельникова
Неравенство (5.36) можно записать в другом виде, раскрыв скобки под интегралами:
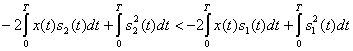
или
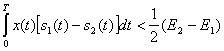 (5.37)
(5.37)
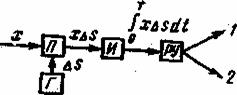
Рис. 5.5. Оптимальный пороговый приемник
Это неравенство совершенно эквивалентно неравенству (5.36), но оно ведет к другой схемной реализации оптимального приемника.
На рис. 5.5 приведена структурная схема приемника, реализующего условия работы (6.37). В этой схеме после операции перемножения (П) и интегрирования (И) производится сравнение полученного результата с постоянным порогом, равным разности энергий сигналов
![]()
Эта схема проще, чем схема рис. 5.4. Однако она обладает тем недостатком, что при изменении уровня сигналов порог нужно автоматически регулировать. Этот недостаток устраняется, если сигналы имеют равную энергию E2=E![]() , тогда порог равен нулю и решающая схема определяет только знак сигнала на выходе.
, тогда порог равен нулю и решающая схема определяет только знак сигнала на выходе.
При ![]() упрощается и схема приемника рис. 5.4. Раскрывая скобки в (5.36), получаем условия оптимального приема в следующем виде:
упрощается и схема приемника рис. 5.4. Раскрывая скобки в (5.36), получаем условия оптимального приема в следующем виде:
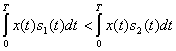 (5.38)
(5.38)
что совпадает с условием (5.33). Таким образом, при ![]() приемник Котельникова превращается в корреляционный (когерентный) (рис. 5.6).
приемник Котельникова превращается в корреляционный (когерентный) (рис. 5.6).
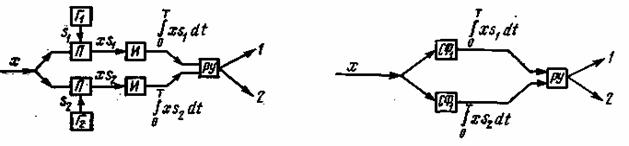
Рис. 5.6. Корреляционный приемник Рис. 5.7. Приемник с согласованными фильтрами
Оптимальный прием можно также реализовать в схеме с согласованными линейными фильтрами (рис. 5.7), импульсные реакции которых должны быть ![]() , где с — постоянный коэффициент (см. § 4.6).
, где с — постоянный коэффициент (см. § 4.6).
Рассмотренные схемы оптимальных приемников относятся к типу когерентных, в них учитывается не только амплитуда, но и фаза высокочастотного сигнала.
Заметим, что в схемах оптимальных приемников отсутствуют фильтры на входе, которые в реальных приемниках всегда имеются. Это означает, что оптимальный приемник при флуктуационных помехах не требует фильтрации на входе. Его помехоустойчивость, как мы увидим дальше, не зависит от ширины полосы пропускания приемника.
5.4. Вероятность ошибки при когерентном приеме двоичных сигналов
Определим вероятность ошибки в системе передачи двоичных сигналов при приеме на оптимальный приемник. Эта вероятность, очевидно, будет минимально возможной и будет характеризовать потенциальную, помехоустойчивость при данном способе передачи. При приеме на реальный приемник помехоустойчивость может быть равна потенциальной, но не может быть больше ее.
Пусть сигнал принимает значения s![]() (t) с вероятностью Р
(t) с вероятностью Р![]() и значения s
и значения s![]() (t) с вероятностью
(t) с вероятностью ![]() . Если передавался сигнал s
. Если передавался сигнал s![]() то согласно условию (5.31) ошибка произойдет в том случае, когда
то согласно условию (5.31) ошибка произойдет в том случае, когда
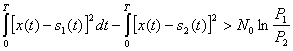 (5.39)
(5.39)
Так как x(t) = s1(t)+w(t), то неравенство (5.39) может быть приведено к виду
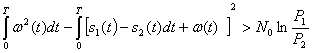
или
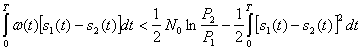 (5.40)
(5.40)
В соответствии с выражениями (5.18) и (5.19) левую, часть неравенства (5.40) можно записать в следующем виде:
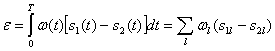 (5.41)
(5.41)
Так как каждый коэффициент ![]() имеет нормальное распределение со средним значением, равным нулю, то сумма (5.41) будет также представлять собой нормальную случайную величину
имеет нормальное распределение со средним значением, равным нулю, то сумма (5.41) будет также представлять собой нормальную случайную величину ![]() с нулевым средним значением и дисперсией
с нулевым средним значением и дисперсией
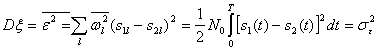 (5.42)
(5.42)
Плотность вероятности случайной величины |![]()
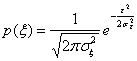
Согласно (5.40) ошибка произойдет при передаче сигнала -s![]() , если
, если
![]()
Величина этой ошибки будет равна:
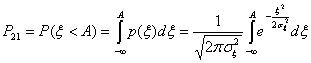 (5,43)
(5,43)
Вводя новую переменную ![]() на основании соотношения (2.29) имеем
на основании соотношения (2.29) имеем
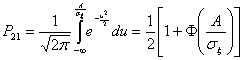
где
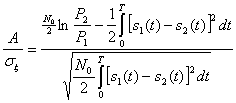
После несложных преобразований окончательно получаем
![]() (5.44)
(5.44)
где
![]() (5.45)
(5.45)
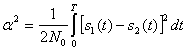 (5.46)
(5.46)
Совершенно аналогично определяется вероятность ошибки при передаче сигнала s![]() (t):
(t):
![]() (5.47)
(5.47)
где
![]() (5.48)
(5.48)
Полная вероятность ошибки при оптимальном приеме бинарных. сигналов s![]() (t) и s
(t) и s![]() (t) будет равна:
(t) будет равна:
![]() (5,49)
(5,49)
или согласно (5.44) и (5.47)
![]() (5.50)
(5.50)
Из полученных формул следует, что вероятность ошибки, определяющая потенциальную помехоустойчивость, зависит от двух величин: ![]() 2 и P
2 и P![]() /P
/P![]() . Первая величина определяется отношением удельной энергии разности сигналов к интенсивности помехи N
. Первая величина определяется отношением удельной энергии разности сигналов к интенсивности помехи N![]() . Чем больше это отношение, тем больше потенциальная помехоустойчивость. Отношение априорных вероятностей P
. Чем больше это отношение, тем больше потенциальная помехоустойчивость. Отношение априорных вероятностей P![]() /P
/P![]() определяется статистическими свойствами передаваемых сообщений.
определяется статистическими свойствами передаваемых сообщений.
Если передаваемые сигналы равновероятны P![]() =P
=P![]() =0,5, то ф-ла (5.50) упрощается и принимает вид
=0,5, то ф-ла (5.50) упрощается и принимает вид
![]() (5.51)
(5.51)
Формулу (5.51) легко получить из геометрических представлений. Как это видно из рис. 5.3, при передаче сигнала s1 ошибка произойдет в том случае, если будет выполняться неравенство r![]() >r2
>r2
или ![]() . Следовательно, вероятность ошибки можно определить как вероятность выполнения одного из этих неравенств, т. е.
. Следовательно, вероятность ошибки можно определить как вероятность выполнения одного из этих неравенств, т. е.
![]()
Умножив обе части неравенства на d, получаем
![]()
где ![]() =
=![]() — случайная величина (5.41), имеющая нормальное распределение с дисперсией
— случайная величина (5.41), имеющая нормальное распределение с дисперсией ![]() (5.42). Тогда на основании (2.32) имеем
(5.42). Тогда на основании (2.32) имеем
![]()
где
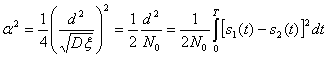
что совпадает с (5.51) и (5.46).
При малой интенсивности помех, когда ![]() , в ф-лах (5.45) и (5.48) вторым членом можно пренебречь. В этом случае ф-ла (5.50) также приводится к ф-ле (5.51). Вероятность ошибки при этом практически не зависит от P
, в ф-лах (5.45) и (5.48) вторым членом можно пренебречь. В этом случае ф-ла (5.50) также приводится к ф-ле (5.51). Вероятность ошибки при этом практически не зависит от P![]() и Р2. при большом уровне помех, когда
и Р2. при большом уровне помех, когда ![]() мало, зависимость вероятности ошибки от отношения априорных вероятностей P
мало, зависимость вероятности ошибки от отношения априорных вероятностей P![]() / Р2 становится заметной. С увеличением этого отношения вероятность ошибки увеличивается [4].
/ Р2 становится заметной. С увеличением этого отношения вероятность ошибки увеличивается [4].
Таким образом, при равновероятных сигналах вероятность ошибки полностью определяется величиной ![]() . Значение этой величины зависит от спектральной плотности помех N0 и передаваемых сигналов s
. Значение этой величины зависит от спектральной плотности помех N0 и передаваемых сигналов s![]() (t) и s
(t) и s![]() (t).
(t).
Для систем с активной паузой, в которых сигналы имеют одинаковую энергию ![]() , выражение для
, выражение для ![]() 2 можно представить в следующем виде:
2 можно представить в следующем виде:
![]() (5.52)
(5.52)
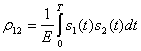 — коэффициент взаимной корреляции
— коэффициент взаимной корреляции
между сигналами, ![]() — отношение энергии сигнала к удельной мощности помехи.
— отношение энергии сигнала к удельной мощности помехи.
Вероятность ошибки для таких систем определяется формулой
![]() (5.53)
(5.53)
Отсюда следует, что при ![]() , т. е.
, т. е. ![]() , система обеспечивает наибольшую потенциальную помехоустойчивость. Эта система с противоположными сигналами. Для нее
, система обеспечивает наибольшую потенциальную помехоустойчивость. Эта система с противоположными сигналами. Для нее ![]() - Практической реализацией системы с противоположными сигналами является система с фазовой манипуляцией.
- Практической реализацией системы с противоположными сигналами является система с фазовой манипуляцией.
Сравнение различных систем передачи дискретных сообщений удобно производить по параметру ![]() 2, представляющему собой приведенное отношение сигнала к помехе на выходе оптимального приемника при заданном способе передачи
2, представляющему собой приведенное отношение сигнала к помехе на выходе оптимального приемника при заданном способе передачи ![]() , или по величине выигрыша
, или по величине выигрыша
![]() (5.54)
(5.54)
где ![]() . Множитель TF определяет выигрыш за счет оптимальной обработки сигнала на приеме, а (1 —
. Множитель TF определяет выигрыш за счет оптимальной обработки сигнала на приеме, а (1 —![]() ) — за счет способа передачи.
) — за счет способа передачи.
В общем виде радиотелеграфный сигнал можно записать
![]() (5.55)
(5.55)
где параметры колебания ![]() принимают определенные значения в зависимости от вида манипуляции. Согласно (5.46) для сигналов (5.55) имеем:
принимают определенные значения в зависимости от вида манипуляции. Согласно (5.46) для сигналов (5.55) имеем:
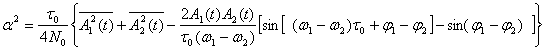 (5.56)
(5.56)
Для амплитудной манипуляции A![]() (t)=A0, A2(t)=0
(t)=A0, A2(t)=0![]()
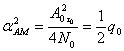
2 -
Для частотной манипуляции A![]() (t)=A2(t)=A0
(t)=A2(t)=A0![]() . При оптимальном выборе разноса частот (
. При оптимальном выборе разноса частот (![]() ), где k— целое
), где k— целое
число и ![]() Тогда на основании (5.56) получаем
Тогда на основании (5.56) получаем
![]()
Для фазовой манипуляции A![]() (t)=A2t)=A0,
(t)=A2t)=A0, ![]() ,
,![]()
![]()
Сравнение полученных формул показывает, что из всех систем передачи бинарных сигналов наибольшую потенциальную помехоустойчивость обеспечивает система с фазовой манипуляцией. По сравнению с ЧМ она позволяет получить двукратный, а по сравнению с AM — четырехкратный выигрыш по мощности.
В системах связи сигнал обычно, составляется из последовательности простых сигналов. Так, в телеграфии каждой букве соответствует кодовая комбинация, состоящая из даты элементарных посылок. Возможны и более сложные комбинации. Если элементарные сигналы, составляющие кодовую комбинацию, независимы, то вероятность ошибочного приема кодовой комбинации определяется следующей формулой:
![]() (5.57)
(5.57)
где ![]() — вероятность ошибки элементарного сигнала, п — число элементарных сигналов в кодовой комбинации (значность кода).
— вероятность ошибки элементарного сигнала, п — число элементарных сигналов в кодовой комбинации (значность кода).
Следует заметить, что вероятность ошибки в рассмотренных выше случаях полностью определяется отношением энергии сигнала к спектральной плотности помехи и не зависит от формы сигнала. В общем случае, когда спектр помехи отличается от равномерного, вероятность ошибки можно уменьшить, изменяя спектр сигнала, т. е. его форму.
5.5. Вероятность ошибки при когерентном приеме многопозиционных сигналов
Работа приемника в многопозиционных системах сводится к различению m сигналов, соответствующих m позициям кода. Схему приемника можно представить себе состоящей из m каналов (ветвей), каждый из которых рассчитан на прием одного определенного сигнала. Одним из примеров многопозиционной системы является система с частотной манипуляцией, в которой сигналы представляют собой гармонические колебания различных частот. Приемник в этой системе содержит m фильтров, настроенных на частоты передаваемых Сигналов. С помощью этих фильтров и осуществляется разделение (различение) сигналов.
Пусть s![]() t), s2(t),..., sm(t) — сигналы, используемые для передачи, и w(t) — аддитивная помеха, воздействующая на приемник. Принимаемые сигналы при этом будут x
t), s2(t),..., sm(t) — сигналы, используемые для передачи, и w(t) — аддитивная помеха, воздействующая на приемник. Принимаемые сигналы при этом будут x![]() ,x
,x![]() ,..., xm. Если передавался сигнал s
,..., xm. Если передавался сигнал s![]() (t), то в первом фильтре будут сигнал и помеха
(t), то в первом фильтре будут сигнал и помеха ![]() ,а в остальных фильтрах — только помеха. Приемник сравнивает принятые сигналы и воспроизводит наибольший из них, т. е. выносит решение о том, что передан k-й сигнал, если
,а в остальных фильтрах — только помеха. Приемник сравнивает принятые сигналы и воспроизводит наибольший из них, т. е. выносит решение о том, что передан k-й сигнал, если ![]() . Поскольку мы предположили, что передавался сигнал s
. Поскольку мы предположили, что передавался сигнал s![]() , это вероятность правильного решения будет равна:
, это вероятность правильного решения будет равна:
![]()
а вероятность ошибки
![]()
Оптимальный когерентный приемник в m-позиционной системе представляет собой многоканальный коррелятор или систему из т согласованных фильтров. Структурная схема такого приемника аналогична схемам рис. 5.6 или рис. 5.7 для двоичных сигналов (разница лишь в числе каналов). В этом случае приемник в соответствии с условиями (5.33) вычисляет функцию взаимной корреляции принятого сигнала x(t) со всеми т опорными сигналами
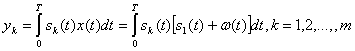 (5.58)
(5.58)
и выдает решение о том, что был передан тот сигнал, для которого корреляция имеет наибольшее значение. Вероятность правильного решения (если передается сигнал s![]() ) будет равна:
) будет равна:
![]() (5.59)
(5.59)
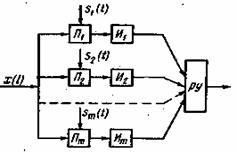
Рис. 5.8. Оптимальный когерентный приемник многопозиционных сигналов
На рис. 5.8 приведена структурная схема когерентного приемника ,много-позиционных сигналов, построенная на базе корреляционной техники. В каждом канале этой схемы производятся синхронное детектирование принятых, сигналов, интегрирование и отсчет в конце каждого элемента сигнала. Полученные отсчеты поступают на схему сравнения (решающее устройство РУ). В результате сравнения выдается решение о том, какой из т сигналов был передан.
Определим вероятность ошибки при оптимальном когерентном приеме Ортогональных m-позиционных сигналов. Будем полагать, что все (возможные сигналы равновероятны и имеют одинаковую энергию Е. Для этого случая условия правильного приема сигнала s![]() согласно (5.33) запишутся
согласно (5.33) запишутся
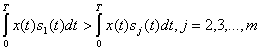
Так как ![]() ,
,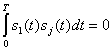 и
и 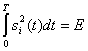 , то это неравенство принимает вид г
, то это неравенство принимает вид г
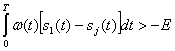 (5.60)
(5.60)
Или
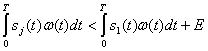 (5.61)
(5.61)
Рассмотрим функцию 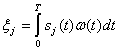 , представляющую собой нормальную случайную величину (помеху на выходе j-го канала) с дисперсией
, представляющую собой нормальную случайную величину (помеху на выходе j-го канала) с дисперсией
![]()
Плотность вероятности величины |![]()
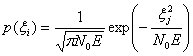
Вероятность того, что помеха в j-м канале не превысит суммарного значения сигнала и помехи в первом канале, т. е. вероятность того, что ![]() , будет равна:
, будет равна:
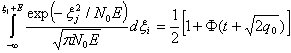 , где
, где
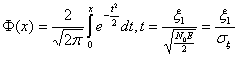 ,
,![]()
Вероятность того, что помеха во всех m— 1 каналах без сигнала не превысит суммарного значения сигнала и помехи в первом канале,
![]()
Интегрирование этого выражения по всем возможным значениям помехи |![]() дает вероятность правильного приема
дает вероятность правильного приема
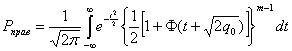 (5.62)
(5.62)
Вероятность ошибки при этом
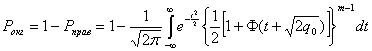 (5.63)
(5.63)
В частном случае при m=2 выражение (5.63) преобразовывается в ф-лу (5.51) для двоичных систем
![]()
При m>2 интеграл в правой части (5.63) может быть вычислен приближенными методами. При относительно больших значениях отношения сигнала к помехе (q0>1) имеет место асимптотическое выражение
![]() (5.64)
(5.64)
При неоптимальном когерентном приеме дискретных сигналов в схеме рис. 5.8 интегратор отсутствует. В этом случае после синхронного детектора ставится фильтр нижних частот и берется отсчет (стробирование) на выходе фильтра в середине посылки. Можно показать, что вероятность ошибки при неоптимальном когерентном приема определяется полученными выше выражениями (5.63) и (5.64), если в последних вместо q0 подставить ![]()
5.6. Некогерентный прием дискретных сигналов
При некогерентном приеме информация о фазе принимаемых сигналов не используется. Такой способ приема применяется в каналах с переменными параметрами, когда фаза сигнала случайно изменяется и ее определение вызывает значительные трудности, а также в каналах с постоянными параметрами с целью упрощения схемы приемника.
Оптимальный некогерентный приемник вычисляет модуль (огибающую) функции взаимной корреляции
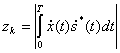
решает, что был передан тот сигнал, для которого z в некоторый момент времени ,t=t0 имеет наибольше![]() ее значение. Пусть передавался сигнал s
ее значение. Пусть передавался сигнал s![]() (t), тогда условие правильного приема этого сигнала можно записать в следующем виде: z
(t), тогда условие правильного приема этого сигнала можно записать в следующем виде: z![]() <z
<z![]()
![]() или
или
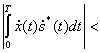
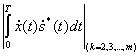 (5.65)
(5.65)
Схема приемника, реализующего условие (5.65), приведена на рис. 5.9. Эта схема содержит т согласованных фильтров (Ф), соответствующих т
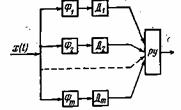
Рис. 5.9. Оптимальный некогерентный приемник m-ичных сигналов
отдельным сигналам. На выходе каждого фильтра получается напряжение, пропорциональное функции взаимной корреляции 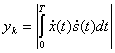 . Амплитудный детектор (Д) выделяет огибающую (модуль) этой функции. Затем производится отсчет и принимается решение.
. Амплитудный детектор (Д) выделяет огибающую (модуль) этой функции. Затем производится отсчет и принимается решение.
Согласно (4.25) имеем
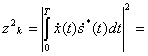
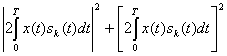
Если передавался сигнал s![]() (t), то x(t)= s
(t), то x(t)= s![]() (t)+w(t) и
(t)+w(t) и
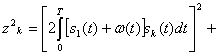
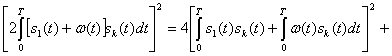
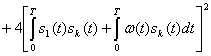
Предположим, что сигналы равновероятны, имеют одинаковую энергию и являются ортогональными в усиленном смысле (2.105). При этих условиях:
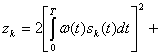
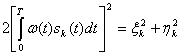
![]() (5.66)
(5.66)
где
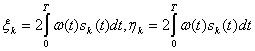 Случайные величины ξ и
Случайные величины ξ и ![]() имеют нормальное распределение s нулевым средним значением и дисперсией, равной
имеют нормальное распределение s нулевым средним значением и дисперсией, равной ![]() . В этом легко убедиться так же, как это было сделано при выводе ф-лы (5.42).
. В этом легко убедиться так же, как это было сделано при выводе ф-лы (5.42).
Случайная величина является суммой квадратов двух независимых случайных величин ![]() и
и ![]() с нормальным распределением, нулевым средним значением и одинаковыми дисперсиями, равными
с нормальным распределением, нулевым средним значением и одинаковыми дисперсиями, равными ![]() . Такая величина, как известно, имеет распределение Рэлея (2.43). В нашем случае
. Такая величина, как известно, имеет распределение Рэлея (2.43). В нашем случае
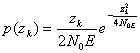 (5.67)
(5.67)
Случайную величину ![]() можно рассматривать как квадрат длины векторной суммы постоянного вектора длиной L=2E и случайного вектора с нормально распределенными независимыми составляющими, имеющими дисперсию
можно рассматривать как квадрат длины векторной суммы постоянного вектора длиной L=2E и случайного вектора с нормально распределенными независимыми составляющими, имеющими дисперсию ![]() =
=![]() . Поэтому величина
. Поэтому величина ![]() подчиняется обобщенному распределению Рэлея (2.48) с плотностью вероятностей
подчиняется обобщенному распределению Рэлея (2.48) с плотностью вероятностей
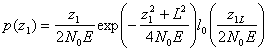 (5.68)
(5.68)
Случайные величины ![]() есть не что иное, как огибающие напряжения в каналах без сигнала, т. е. огибающие помех. Так как помехи мы считаем гауссовыми, то этим и объясняется, что
есть не что иное, как огибающие напряжения в каналах без сигнала, т. е. огибающие помех. Так как помехи мы считаем гауссовыми, то этим и объясняется, что ![]() будут иметь рэлеевское распределение. Случайная величина
будут иметь рэлеевское распределение. Случайная величина ![]() есть огибающая суммарного колебания сигнала и помехи в канале с сигналом, поэтому она и подчиняется закону обобщенного распределения Рэлея.
есть огибающая суммарного колебания сигнала и помехи в канале с сигналом, поэтому она и подчиняется закону обобщенного распределения Рэлея.
Теперь можно определить вероятность ошибки при некогерентном приеме. В общем случае эта вероятность будет равна:
![]() (5.69)
(5.69)
При бинарной передаче (m=2)
![]()
Для вычисления вероятности ошибки сначала вычисляется при некотором фиксированном значении ![]() вероятность того, что
вероятность того, что ![]() >
>![]() . Эта вероятность выражается интегралом
. Эта вероятность выражается интегралом
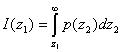
который имеет различные значения при различных ![]() . Для того чтобы найти полную вероятность
. Для того чтобы найти полную вероятность ![]() >
>![]() , необходимо
, необходимо ![]() усреднить по всем возможным значениям
усреднить по всем возможным значениям ![]() в соответствии с распределением
в соответствии с распределением ![]() Таким образом,
Таким образом,
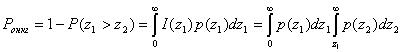 (5.70)
(5.70)
После подстановки в (5.70) выражений ![]() и
и ![]() в соответствии с (5.67) и (5.68) и интегрирования получаем следующее выражение для вероятности ошибки при оптимальном некогерентном приеме двоичных сигналов:
в соответствии с (5.67) и (5.68) и интегрирования получаем следующее выражение для вероятности ошибки при оптимальном некогерентном приеме двоичных сигналов:
![]() (5.71)
(5.71)
где ![]() .
.
Для m-позиционных систем справедливо приближенное соотношение
![]()
Из уравнения ф-л (5.64) и (5.72) следует, что вероятность ошибки в многопозиционных системах Ротприближенно определяется через вероятность ошибки в соответствующей двоичной системе P![]() . Это соотношение имеет следующий вид:
. Это соотношение имеет следующий вид:
![]() (5.73)
(5.73)
На рис. 5.10 приведены графики зависимости вероятности ошибки в двоичной системе с активной паузой от отношения сигнала к помехе при когерентном и некогерентном приемах. Сравнение кривых показывает, что оптимальный когерентный прием несущественно отличается по помехоустойчивости от оптимального некогерентного приема. При неоптимальном приеме и большом уровне помех (q<1) это различие, как уже отмечалось, может быть значительным.
5.7. Передача дискретных сигналов по каналам с переменными параметрами
До сих пор мы рассматривали системы передачи информации, в которых параметры канала неизменны. Вероятность ошибки в таких системах обусловлена лишь наличием аддитивных помех. Оптимальный приемник использует все параметры сигнала и обеспечивает максимально возможную помехоустойчивость. В реальных условиях параметры канала и соответственно параметры сигнала могут случайно изменяться. Эффективное использование параметров сигнала на приеме в этих условиях затрудняется и помехоустойчивость неизбежно ухудшается.
В реальных каналах сигналы на вход приемника могут приходить по разным путям с различными затуханиями μк и различными запаздываниями τк. Принимаемый сигнал x(t) в этом случае можно представить в виде суммы
![]() (5.74)
(5.74)
где μк и τк. — случайные процессы, вообще говоря, зависящие от времени, w(t) — аддитивная помеха. Каналы, описываемые выражением (5.74), называются многолучевыми.
Во многих случаях имеет место только один путь распространения
![]() (5.75)
(5.75)
Такие каналы называются однолучевыми. Если величины μ и τ фиксированы во времени, то имеем канал с постоянными параметрами. К таким каналам можно отнести каналы проводной связи и укв каналы при передаче в пределах прямой видимости.
Почти все виды радиоканалов относятся к каналам со случайно изменяющимися параметрами. К этому классу каналов принадлежат коротковолновые линии связи, в которых благодаря изменению состояния ионосферы происходят непрерывные колебания амплитуды сигнала в точке приема. Случайные изменения условий распространения радиоволн имеют место на ультракоротких волнах, а также на средних и даже длинных волнах.
Любые изменения коэффициента передачи и времени распространения сигналов вызывают флуктуации сигналов на выходе каналов и могут рассматриваться как действие помех. Изменения коэффициента μ проявляются в виде флуктуации амплитуды сигнала и называются мультипликативной помехой. Случайные задержки лучей вызывают фазовые и временные флуктуации сигналов.
Воздействие мультипликативной помехи на передаваемый сигнал s можно рассматривать как модуляцию этого сигнала случайным процессом μ . Такую помеху можно свести к аддитивной:
![]()
где ![]() — эквивалентная аддитивная помеха, равная
— эквивалентная аддитивная помеха, равная ![]() Эквивалентная помеха
Эквивалентная помеха ![]() представляется произведением случайного процесса
представляется произведением случайного процесса ![]() на детерминированную функцию времени s. Это значит, что
на детерминированную функцию времени s. Это значит, что ![]() — нестационарный процесс и что все его распределения и их моменты зависят от времени. Практически это означает, что при анализе нужно после усреднения по множеству прибегать к усреднению по времени. Заметим также, что μ есть случайный процесс с ненулевым средним
— нестационарный процесс и что все его распределения и их моменты зависят от времени. Практически это означает, что при анализе нужно после усреднения по множеству прибегать к усреднению по времени. Заметим также, что μ есть случайный процесс с ненулевым средним ![]() и что
и что ![]() . Процесс
. Процесс ![]() имеет уже нулевое среднее и соответственно смещенное распределение. Величины μ и ξ безразмерны, тогда как
имеет уже нулевое среднее и соответственно смещенное распределение. Величины μ и ξ безразмерны, тогда как ![]() имеет размерность сигнала.
имеет размерность сигнала.
Эквивалентная мощность мультипликативной помехи, очевидно, будет равна ее дисперсии:
![]()
Отношение сигнала к эквивалентной помехе при этом будет равно:
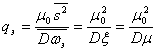 (5.76)
(5.76)
т. е. оно определяется только средним значением и дисперсией процесса μ(t), характеризующего мультипликативную помеху.
Распространенным явлением, приводящим к случайным колебаниям параметров сигнала в точке приема, является многолучевое распространение радиоволн. Многолучевость — основная причина замирания сигнала. Вследствие разностей хода лучей, приходящих от передатчика к приемнику, сигнал в приемной антенне представляет собой сумму отдельных колебаний с различными фазами и амплитудами. Интерференция этих колебаний в условиях, когда разности хода лучей не остаются постоянными, и является основной причиной флуктуации как амплитуд, так и фаз составляющих сигнала. В зависимости от ширины спектра сигнала F и свойств канала различают общие (или гладкие) и селективные замирания, которые, в свою очередь, могут быть быстрыми и медленными.
Общие замирания имеют место, когда время запаздывания лучей ![]() . При этом коэффициент передачи канала μ (или амплитуда сигнала) и фаза сигнала ф для всех частотных составляющих изменяются одинаково. (При большом числе лучей можно считать, что случайная величина ф имеет равномерную плотность вероятности на интервале от 0 до 2π, а μ- распределение Рэлея
. При этом коэффициент передачи канала μ (или амплитуда сигнала) и фаза сигнала ф для всех частотных составляющих изменяются одинаково. (При большом числе лучей можно считать, что случайная величина ф имеет равномерную плотность вероятности на интервале от 0 до 2π, а μ- распределение Рэлея
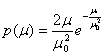 (5.77)
(5.77)
где ![]() — среднеквадратичное значение коэффициента передачи μ .
— среднеквадратичное значение коэффициента передачи μ .
В ряде случаев сигнал в точке приема состоит из двух составляющих: регулярной с медленно изменяющимися параметрами и рассеянной быстро флуктуирующей составляющей. В этих случаях коэффициент передачи μ описывается обобщенным распределением Рэлея
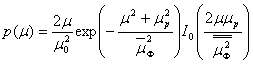 (5.78)
(5.78)
где ![]() — регулярная составляющая коэффициента передачи,
— регулярная составляющая коэффициента передачи,![]() среднее значение квадрата флуктуирующей составляющей,
среднее значение квадрата флуктуирующей составляющей,![]() среднее квадратичное значение μ. Фаза сигнала φ в этом случае распределена неравномерно.
среднее квадратичное значение μ. Фаза сигнала φ в этом случае распределена неравномерно.
В случае сильных замираний, когда ![]() , распределение (5.78) приближается к рэлеевскому (5.77). Такие замирания иногда называют рэлеевскими. Замирания, подчиняющиеся обобщенному закону Рэлея, называют квазирэлеевскими.
, распределение (5.78) приближается к рэлеевскому (5.77). Такие замирания иногда называют рэлеевскими. Замирания, подчиняющиеся обобщенному закону Рэлея, называют квазирэлеевскими.
Для слабых замираний, когда ![]() , на основании (5.78) получаем распределение, близкое к нормальному:
, на основании (5.78) получаем распределение, близкое к нормальному:
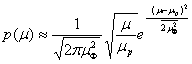
Слабые замирания поэтому называют гауссовыми замираниями.
Согласно экспериментальным данным в диапазонах средних и коротких волн рэлеевские и квазирэлеевские замирания встречаются примерно одинаково часто. В укв диапазоне при дальнем ионосферном или тропосферном распространении преобладают рэлеевские замирания, при ближнем распространении — квазирэлеевские.
Селективные замирания наблюдаются тогда, когда время запаздывания лучей соизмеримо с величиной 1/F. В этом случае амплитуды и фазы частотных составляющих сигнала изменяются независимо друг от друга. При быстрых замираниях амплитуды и фазы смежных элементов сигнала некоррелированы между собой, а при медленных замираниях они изменяются одинаково.
В случае медленных замираний, которые мы и рассмотрим, коэффициент передачи канала μ и фазы сигнала φ практически не изменяются за время длительности нескольких элементов сигнала. Анализ ранее принятых элементов сигнала позволяет с достаточной степенью точности предсказать ожидаемые параметры следующего элемента. В этих условиях прием может быть осуществлен так же, как если бы замирания отсутствовали, и оптимальными будут схемы, рассмотренные в предыдущих параграфах, с той лишь разницей, что в схемах должны производиться непрерывные регулировки μ (регулировка усиления) и φ (регулировка фазы) в соответствии с ожидаемыми значениями μ и φ. В связи с трудностями подстройки фазы более широкое применение находят некогерентные методы приема, в которых сведения о фазе сигнала не используются. В каналах, где случайно изменяется только фаза сигнала, некогерентный прием является оптимальным (см. § 5.6).
Формулы, определяющие вероятность ошибки элемента сигнала при медленных замираниях для данного значения q![]() , остаются теми же, что и в канале без замираний. Но в процессе замираний величина q
, остаются теми же, что и в канале без замираний. Но в процессе замираний величина q![]() изменяется пропорционально μ2. Поэтому для определения полной вероятности ошибки необходимо усреднить вероятность P
изменяется пропорционально μ2. Поэтому для определения полной вероятности ошибки необходимо усреднить вероятность P![]() ( q
( q![]() ) в соответствии с распределением р(μ), т. е.
) в соответствии с распределением р(μ), т. е.
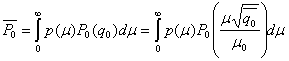 (5.79)
(5.79)
где учтено, что ![]() .
.
Найдем в качестве примера вероятность ошибки при когерентном приеме бинарных сигналов в условиях медленных рэлеевских замираний. Подставив в (5.79) выражение для вероятности ошибки (5.53) и плотность вероятности р(μ ) из (5.77), получим
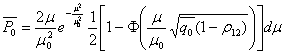
Интегрирование по частям дает следующий результат:
(5.80)
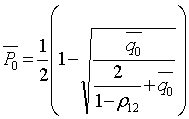 (5.80)
(5.80)
При q![]() >>1 имеем приближенную формулу
>>1 имеем приближенную формулу
![]()
При некогерентном приеме для систем с активной паузой вероятность ошибки при медленных рэлеевских замираниях определяется путем усреднения (5.71) по μ в соответствии с (5.77)
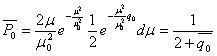 (5.81)
(5.81)
График зависимости (5.81) приведен на рис. 5.10. Из сравнения кривых видно, что наличие замираний сигнала значительно снижает помехоустойчивость системы связи.
В случае квазирэлеевских замираний плотность вероятности ![]() определяется обобщенным распределением Рэлея (5.78). Для этого случая полная вероятность ошибки при некогерентном приеме бинарных сигналов в соответствии с (5.78), (5.71) и (5.79) будет
определяется обобщенным распределением Рэлея (5.78). Для этого случая полная вероятность ошибки при некогерентном приеме бинарных сигналов в соответствии с (5.78), (5.71) и (5.79) будет
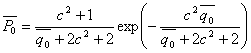 (5.82)
(5.82)
где ![]()
При с=0 это выражение переходит в ф-лу (5.81) для рэлеевских замирании.
Канал с квазирэлеевскими замираниями является промежуточным случаем между каналом без замираний и каналом с рэлеевскими замираниями. Графики вероятности ошибки для этого случая на рис. 5.10 будут размещаться между кривыми б и в. При малых значениях с графики будут ближе к кривой в, а при больших — к кривой б.
Естественным методом устранения мультипликативной помехи, в том числе и замираний, является применение автоматическойрегулировки усиления (АРУ). При отсутствии аддитивной помехи идеальная система АРУ позволяет полностью устранять мультипликативную помеху. Действие такой системы должно сводиться к умножению сигнала х на ![]() , т. е.
, т. е. ![]() . При наличии аддитивной помехи
. При наличии аддитивной помехи ![]() Здесь хотя и получается сигнал постоянной интенсивности, но с флуктуирующей по интенсивности аддитивной помехой.
Здесь хотя и получается сигнал постоянной интенсивности, но с флуктуирующей по интенсивности аддитивной помехой.
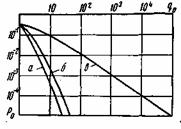
Рис. 5.10. Зависимость вероятности ошибки в бинарной системе с активной паузой от отношения сигнала к помехе: когерентный прием (а), некогерентный прием (б), некогерентный прием в канале с рэлеев-скими замираниями (в)
Эффективной мерой борьбы с замираниями является разнесенный прием сигналов. Суть его состоит в том, что на приеме переданное сообщение воспроизводится не по одному принятому сигналу, а по двум или нескольким сигналам, несущим одно и то же сообщение. Этими сигналами могут быть сигналы нескольких передатчиков, работающих на различных частотах (разнесение по частоте), или сигналы одного и того же передатчика, принятые на различные антенны, разнесенные по пространству или по поляризации. Возможно также и разнесение по времени (например, повторения передачи).
Обработка нескольких сигналов на приеме в общем случае сводится к суммированию с весом. В частных случаях это может быть простое сложение принятых сигналов или выбор наибольшего из них.
5.8. Оптимальный прием непрерывных сообщений
Определим условия оптимального приема непрерывных сообщений. Пусть сообщение представляет собой некоторое колебание (ut), которое может непрерывно изменяться со временем и принимать любую форму. С такими сообщениями мы встречаемся, например, в телефонии, телевидении, телеметрии.
Для простоты анализа будем считать, что функция u(t) принимает значения в пределах от +1 до -1. Будем также полагать, что передаваемое колебание является периодическим с периодом (это всегда можно допустить, взяв Т достаточно большим) и что спектр этого колебания ограничен частотами от i![]() /T до i
/T до i![]() /T. При этих условиях функцию u(t) можно представить согласно (2.70) в виде
/T. При этих условиях функцию u(t) можно представить согласно (2.70) в виде
![]() (5.83)
(5.83)
где ![]() —некоторые параметры, определяющие передаваемое колебание и(t), φe(t)—единичные ортогональные функции,
—некоторые параметры, определяющие передаваемое колебание и(t), φe(t)—единичные ортогональные функции, ![]()
Для передачи по каналу колебание u(t) преобразовывается в сигнал s(u, t). Поскольку колебание (5.83) определяется ![]() параметрами
параметрами ![]() , то сигнал будет зависеть от этих параметров:
, то сигнал будет зависеть от этих параметров: ![]() . Принятый сигнал вследствие наложения помехи ω(t) равен
. Принятый сигнал вследствие наложения помехи ω(t) равен ![]() .
.
Задача заключается в том, чтобы по колебанию x(t) восстановить переданное сообщение u(t) с возможно большей точностью. Как мы уже установили, самое большее, что может сделать приемник на основе анализа принятого сигнала x(t), это вычислить распределение вероятностей P(s/x) для всех возможных реализаций u(t). При передаче непрерывных колебаний функция P(s/x) есть плотность распределения вероятности.
Согласно (5.2) оптимальный приемник вычисляет апостериорное распределение вероятностей P(s/x) и выдает на выходе ту реализацию сообщения u(t), при которой функция P(s/x) будет максимальна. При этом приемник не обязательно должен определять апостериорное распределение вероятностей P(s/x) в явном виде— он должен выдавать на выходе результат, эквивалентный этой функции.
Согласно формуле Байеса (5.3) выражение P(s/x) для рассматриваемого случая можно записать в следующем виде:
![]() (5.84)
(5.84)
где k — некоторая постоянная, которая может быть вычислена из условия нормировки ![]() .
.
Полагаем, что все возможные сообщения u(t) и соответствующие им сигналы s(u, t) равновероятны, т. е. P(s)=const для всех реализаций u(t), лежащих в интервале (-1, +1). При этом согласно (5.26) и (5.84)
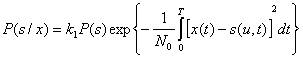 (5.85)
(5.85)
Отсюда максимуму апостериорной вероятности P(s/x) соответствует минимум по u(t) величины
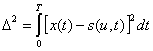 (5.86)
(5.86)
Таким образом, оптимальный приемник должен воспроизводить сообщение u(t), при котором среднеквадратическое отклонение Δ2 имеет минимальное значение. При отсутствии то мех такой приемник воспроизводит сообщение без искажений (без ошибок): x(t)=s(u, t), v(t)=u(t) и Δ2=0, при наличии помех ошибка будет минимальной.
Из выражения (5.86) следует, что операции оптимальной фильтрации и детектирования дают достаточное решение задачи об извлечении максимальной информации из принятого сигнала x(t) относительно переданного сообщения u(t). Структурная схема приемника с, оптимальным фильтром приведена на рис. 5.11.
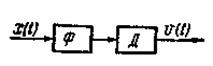
Рис. 5.11. Структурная схема оптимального приемника непрерывных сигналов
Теория линейной фильтрации. Колмогорова—Винера для стационарных процессов была рассмотрена в § 4.8. Согласно этой теории коэффициент передачи оптимального фильтра определяется выражением (4.63), а минимальная среднеквадратическая ошибка фильтрации — выражением (4.65). Практическая реализация таких фильтров сопряжена с большими трудностями. А если учесть, что реальные модулированные сигналы не являются стационарными, то задача построения оптимального фильтра на базе лилейной теории становится практически неразрешимой. Недостатком этой теории является и то, что линейный фильтр оптимален для сигнала s(u, t), а не для самого сообщения u(t). Поэтому представляет интерес рассмотреть другие пути построения оптимального приемника непрерывных сообщений.
Запишем выражение (5.85) в другом виде:
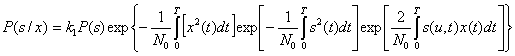 (5.87)
(5.87)
Первый экспоненциальный множитель, не зависящий от и, может быть включен в постоянную k![]() . Второй множитель вообще не представляет операции над x(t), он может быть вынесен в виде отдельного множителя, подобного априорной вероятности во многих случаях этот множитель, равный ехр(-E/N0), где Е — энергия сигнала, также можно включить в постоянную k
. Второй множитель вообще не представляет операции над x(t), он может быть вынесен в виде отдельного множителя, подобного априорной вероятности во многих случаях этот множитель, равный ехр(-E/N0), где Е — энергия сигнала, также можно включить в постоянную k![]() . Следовательно, выражение (5.87) можно записать
. Следовательно, выражение (5.87) можно записать
![]() (5.58)
(5.58)
где 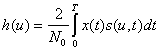 (5.89)
(5.89)
Отсюда следует, что при известной априорной вероятности определение апостериорной вероятности сводится к вычислению функции h(u), т. е. к вычислению взаимной корреляции между принятым сигналом x(t) и переданным (ожидаемым) сигналом s(u, t).. Иными словами, корреляционная обработка сигнала является оптимальной.
Функция h(u) легко вычисляется, когда сигнал является полностью известным. Достигается это с помощью коррелятора или согласованного фильтра. Такая ситуация обычно имеет место при передаче дискретных сообщений (§ 5.3).
При передаче непрерывных сообщений сигнал s(u, t) не является полностью известным. Однако мы располагаем некоторой, априорной информацией об этом сигнале. Известны, например, несущая частота, вид модуляции, ширина спектра сигнала и т. п. Недостающую часть информации можно получить в результате наблюдения над принятой реализацией сигнала x(t) за предшествующий промежуток времени. В результате имеется возможность на приеме определить оценку сигнала s(v, t) и вычислить функцию h(v) для этой оценки:
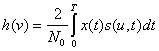 (5.90)
(5.90)
Функцию h(v) можно вычислить с помощью фильтра с переменными параметрами (рис. 5.12) или схемы следящего коррелятора (рис. 5.1.3). Каждая из этих схем имеет основной информационный канал, на выходе которого получается оценочное значение v(t) передаваемого сообщения u(t), и канал обратной связи, с помощью которого в схеме рис. 5.13
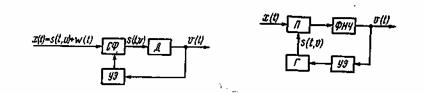
Рис. 5.12. Структурная схема Рис. 5.13. Структурная
приемника со следящим филь- схема следящего корре-
тром ляционного приемника
формируется опорный сигнал s(v, t), а в схеме рис. 5.12 производится изменение параметров фильтра. В схеме рис. 5.12 с помощью управляющего элемента (УЭ) изменяют параметры фильтра (СФ) так, чтобы он был согласован с непрерывно изменяющимся ожидаемым сигналом s(t, v). В схеме же рис. 5.1З с помощью УЭ изменяется модулируемый параметр несущего колебания, формируемого генератором Г. При частотной модуляций, например, этим параметром является частота, при времяимпульсной модуляции — временной сдвиг импульсов и т. п. Фильтр нижних частот (ФНЧ),в этой схеме выполняет роль интегратора на интервале наблюдения Т, который связан с максимальной частотой Fm в спектре передаваемого сообщения соотношением Т=1/2Fm.
При различных видах модуляции принцип следящего приема остается тем же. Вид модуляции определяет параметр, за которым должно осуществляться слежение. Схемы следящего приема позволяют практически реализовать помехоустойчивость, близкую к потенциальной, и тем самым, как будет показано в § 9.3, снизить порог помехоустойчивости до его предельного значения.
До сих пор мы предполагали, что амплитуда и фаза несущего колебания сигнала неизменны во времени, а помеха имеет постоянную спектральную плотность ![]() . В каналах с переменными параметрами амплитуда и фаза сигнала изменяются во времени. В этом случае схемы рис. 5.12 и рис. 5.13 должны быть дополнены устройством автоматической регулировки уровня сигнала и системой фазовой автоподстройки. При неизвестном значении
. В каналах с переменными параметрами амплитуда и фаза сигнала изменяются во времени. В этом случае схемы рис. 5.12 и рис. 5.13 должны быть дополнены устройством автоматической регулировки уровня сигнала и системой фазовой автоподстройки. При неизвестном значении ![]() или его изменении во времени для осуществления оптимального приема необходимо специальное устройство измерения и выравнивания интенсивности помех. В частности, для сосредоточенных по спектру или во времени помех с резко выраженной интенсивностью, достаточно близкой к оптимальной оказывается схема со стиранием участков спектра или длительности сигнала, пораженных помехой (см. § 8.8).
или его изменении во времени для осуществления оптимального приема необходимо специальное устройство измерения и выравнивания интенсивности помех. В частности, для сосредоточенных по спектру или во времени помех с резко выраженной интенсивностью, достаточно близкой к оптимальной оказывается схема со стиранием участков спектра или длительности сигнала, пораженных помехой (см. § 8.8).
Таким образом, в общем случае при оптимальном приеме необходимо осуществлять слежение за формой как сигнала, так и помехи. Чем большее число параметров при этом будет учтено, тем выше будет помехоустойчивость. При этом схема приемника должна быть адаптивной.
Оптимальный приемник представляет собой устройство, воспроизводящее переданное сообщение u(t) с наименьшей ошибкой. Так как полезный сигнал s(u, t) зависит от u(t) нелинейно, то оптимальный приемник также должен быть нелинейным устройством (нелинейным фильтром). Примером такого устройства (фильтра) является рассмотренный выше следящий приемник. Таким образом, теорию оптимального приема можно рассматривать как теорию оптимальной нелинейной фильтрации.
Общая теория нелинейной фильтрации охватывает разнообразные и весьма сложные задачи. В настоящее время эта теория разработана лишь для случаев, когда переданное сообщение u(t) представляет собой марковский или нормальный случайный процесс [9].
Вопросы для повторения
1. Что называется помехоустойчивостью связи? Какой приемник называется оптимальным?
2. Что такое симметричный и несимметричный канал; канал с памятью и канал со стиранием?
3. Перечислите основные статистические критерии приема сигналов. Сформулируйте критерий Котельникова.
4. При каких условиях критерий минимального среднего риска совпадает с критерием Котельникова?
5. Как определяется полная вероятность ошибки при передаче дискретных сообщений?
6. Какие схемы приемников реализуют условия оптимального приема?
7. При каких условиях схема оптимального приемника Котельникова переходит в схему корреляционного приемника?
8. Дайте сравнительную оценку помехоустойчивости связи при различных видах манипуляции: AM, ЧМ и ФМ.
9. Что называется мультипликативной помехой? Как такую помеху можно свести к эквивалентной аддитивной помехе?
10. Какие виды замираний Вам известны? Поясните причины появления замираний.
11. В чем разница между рэлеевскими и квазирэлеевскими замираниями?
12. Поясните метод вычисления вероятности ошибки при медленных общих замираниях.
13. Сформулируйте условия оптимального приема непрерывных сообщений.
14. Какие трудности возникают при реализации Оптимального приемника непрерывных сигналов?
15. Нарисуйте структурную схему следящего приемника и поясните принцип его работы.

