6.1. Круглый волновод

Волновод – закрытая направляющая система, в которой распространение энергии ограничивается в поперечном направлении. Это однопроводная система, следовательно в ней могут распространяться поперечные электрические (TE,H) и поперечные магнитные (TH,E) волны, а поперечные электромагнитные волны распространяться не могут. В волноводах преобладают токи смещения, токи проводимости незначительны, они протекают по проводящим стенкам волновода и замыкаются токами смещения вследствие непрерывности линий тока. Наиболее распространенными являются прямоугольные и круглые волноводы. Особенность волновода, как направляющей системы, состоит в том, что в нем могут распространяться волны с длиной волны не превышающей критическую. Аналз проводится для гармонических колебаний, множитель опущен.

Для анализа свойств волновода рассмотрим сначала особенности распространения волн между двумя бесконечными проводящими плоскостями (рис. 6.1). Используя уравнения Максвелла получим волновое уравнение для этой структуры.

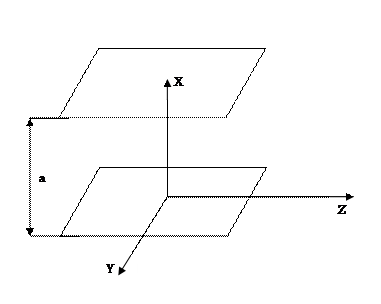
Рис. 6.1. Бесконечные проводящие плоскости.

Рассмотрим поперечно-магнитное поле для системы (рис. 6.1). Волновое уравнение относительно составляющей запишется в виде:

(6.1)

где 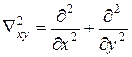- оператор Лапласа в прямоугольной системе координат; - волновое число, тогда (6.1) примет вид

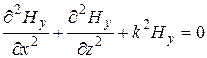. (6.2)

В соответствии с рисунком В.1 предположим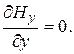

Уравнение (6.2) – дифференциальное уравнение 2-го порядка с разделяющимися переменными, которое после соответствующих преобразований представляется в виде системы двух дифференциальных уравнений:

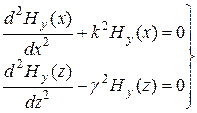, (6.3)

где - постоянная распространения, а - поперечное волновое число.

Решение системы (6.3) представляется в виде:

. (6.4)

Первый сомножитель в (6.4) определяет структуру поля в поперечном сечении системы, а второй – описывает распространение волны вдоль оси z. Учитывая, что при волна затухает, полагаем D=0.

Чтобы найти постоянные интегрирования в (6.4), необходимо воспользоваться граничными условиями для составляющих поля. Известно, что касательные составляющие электрического поля на проводящих поверхностях обращаются в нуль, т.е.

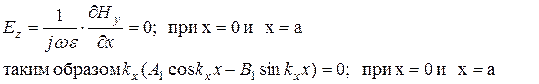(6.5)

Условие (6.5) выполнимо при . В этом случае не только на проводящих плоскостях, но и в пространстве между ними, т.е. .

Это решение уравнений (6.3) является не единственно возможным. Условиям (6.5) можно удовлетворить и при , т.е. необходимо выполнение равенства:

, при х=0 и х=а. (6.6)

Левая часть (6.6) обращается в нуль при х=0 и х=а, если

и ,

откуда вытекает , где m=0,1,2… (6.7)

Таким образом получим:

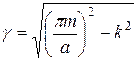, m=0,1,2… (6.8)

Легко заметить, что при постоянная распространения становится мнимой величиной, поперечно-магнитное поле в этом случае будет иметь волновой характер. Так как m – любое целое число, то в пространстве между параллельными проводящими плоскостями может существовать бесчисленное множество типов волн (мод), характеризующихся различными значениями m и различной структурой поля.

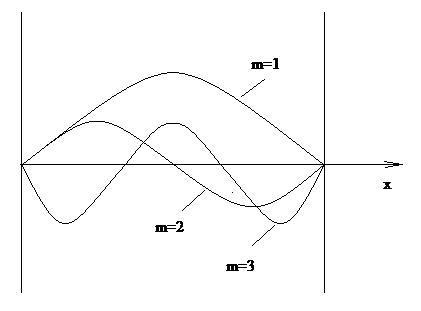
Рис. 6.2. Волны между параллельными плоскостями.

В анализируемой системе могут распространяться только волны, удовлетворяющие условию:

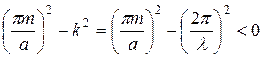, (6.9)

откуда при m=1 получаем .

Таким образом, система является фильтром верхних частот, в системе существует частота отсечки, или критическая частота, удовлетворяющая (6.8).

Приведенный анализ позволяет сделать важнейшие выводы:

• возможность распространения волн между двумя параллельными плоскостями определяется расстоянием между этими плоскостями;
• в пространстве между проводящими плоскостями могут распространяться поперечно-электрические и поперечно-магнитные волны;
• множество распространяющихся в системе волн (мод) является дискретным;
• распространение Н- и Е-волн начинается с определенной частоты, называемой критической, Н- и Е-волны с частотой ниже критической не распространяются;
• критическая частота (длина волны) определяется расстоянием между проводящими плоскостями.

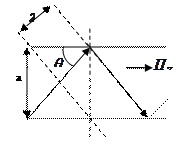
При распространении энергии между проводящими плоскостями можно выделить 3 режима (рис. 6.3): распространение, близкое к прямолинейному, режим многократных отражений, критический режим.

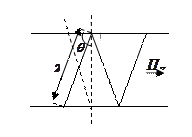
а) б) в)

Рис. 6.3 – Распространение электромагнитной волны: а) близкое к прямолинейному; б) режим многократных отражений; в) критический режим (стоячая волна)

Приведенный анализ справедлив для изучения процессов в волноводах и световодах, в любых системах, в которых распространяются поперечные волны.

Проще всего приведенный анализ распространить на прямоугольный волновод (рис. 6.4). Анализ проводится для гармонического колебания.

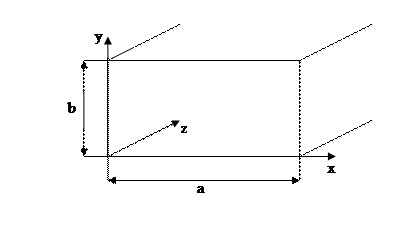
Рис. 6.4. Прямоугольный волновод

Рассмотрим Н-волны. Как и для системы из параллельных плоскостей, при анализе процессов в волноводе из уравнений Максвелла получаем волновое уравнение относительно составляющей :

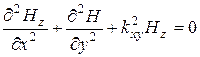, (6.10)

где - поперечное волновое число, согласно (6.7) .

Зависимость представляется в виде:

,

где .

Дифференциальное уравнение (6.10) сводится к системе двух уравнений:

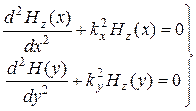. (6.11)

Решение этих уравнений представляется в виде:

;

; (6.12)

.

Учитывая граничные условия для составляющих электрического поля: при y=0, y=b и при x=а и х=0 и связь между и поперечными составляющими имеет вид:

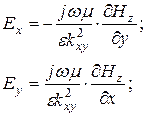(6.13)

получим составляющую поля :

; (6.14)

где .

Учитывая (6.13) можно получить и другие составляющие поля. При m=n=0 все составляющие поля, кроме , обращаются в 0, следовательно, m и n могут принимать любые значения, равные 0, 1, 2…, но они не должны одновременно равняться нулю. Аналогичные рассуждения можно привести и для Е-волн.

Таким образом, в прямоугольном волноводе существует бесчисленное множество поперечно-электрических, или Н-волн, и поперечно-магнитных, или Е-волн, которые характеризуются разными значениями m и n. Вдоль сторон a и b распределение поля имеет форму стоячей волны, причем m определяет число полуволн (вариаций поля), укладывающихся на интервале , а n – число полуволн на интервале . Поле будет распространяться по оси z в виде бегущей волны, если - мнимая величина:

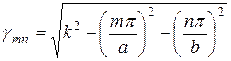. (6.15)

Для того, чтобы волна распространялась вдоль оси z необходимо выполнение условия

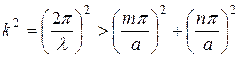. (6.16)

Таким образом, в волноводе, как и в системе из двух параллельных плоскостей, может распространяться дискретный набор типов волн (мод), условие их распространения определяется (6.16), этим же соотношением определяется длина волны распространяющихся колебаний. В отличие от системы двух параллельных плоскостей длина волны ограничивается уже двумя параметрами a и b. В волноводе невозможно распространение ТЕМ-волны. После преобразований (6.16) получим выражение для критической частоты волны. Волны, частоты которых меньше , в волноводе не распространяются.

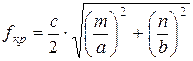, m=0, 1, 2… (6.17)

.

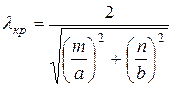Возможность распространения волн в прямоугольном волноводе определяется его поперечными размерами. Волна, имеющая простейшую структуру поля и наибольшую длину, называется основной, такой волной в прямоугольном волноводе является волна . Низшие типы волн имеют затухание меньшее, чем высшие типы. Возбуждение в волноводах высших типов волн приводит к увеличению потерь, эти волны возбуждаются при наличии неоднородностей. В волноводе основными являются токи смещения, токи проводимости, протекающие по стенкам волноводов незначительны, т.е. . Токи проводимости в волноводах являются поверхностными, они протекают по очень тонкому поверхностному слою его стенок (вследствие поверхностного эффекта). Для уменьшения потерь в волноводе его спинки изготавливаются с высокой степенью чистоты и покрываются тонким слоем металла с высокой проводимостью, как правило серебром.

6.1. Круглый волновод

В круглом волноводе электромагнитное поле представляется в виде совокупности поперечно – электрических (Н – волны) и поперечно – магнитных (Е - волны) различных типов.

Так же и в теории прямоугольных волноводов, из уравнений Максвелла можно получить волновое уравнение для или составляющих. Рассмотрим Н – волны, для которых волновое уравнение имеет вид

, (6.18)

где - поперечное волновое число, - оператор Лапласа в цилиндрической системе координат, тогда (6.18) запишется:

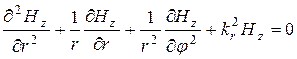(6.19)

Как и в предыдущем анализе рассматриваем гармонические колебания, волна распространяется вдоль оси Z, т. е. .

Решение волнового уравнения в цилиндрической системе координат представляется совокупностью функций Бесселя и гармонических функций.

(6.20)

Функции Бесселя второго рода при обращаются в бесконечность. Из физических условий ясно, что поле в центре волновода ( ) должно иметь конечное значение, т. е. . Тогда (В.20) будет иметь вид:

. (6.21)

Так как функция не должна изменяться при замене на , то может быть лишь целым числом, т. е. Для рассматриваемой системы должно выполняться граничное условие , при , это условие выполнимо 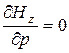при

при , или ,

Таким образом, делаем вывод, что граничное условие выполнимо при обращении производных соответствующих производных функций Бесселя в нуль, т. е. аргумент функции является корнем производной функции Бесселя первого рода порядка , обозначим этот корень . Учитывая соотношение , определяем критическую частоту в круглом волноводе

. (6.22)

Индекс m определяет порядок функции Бесселя, а n – номер её корня. В структуре поля m определяет число полуволн вдоль диаметра волновода, а n – вдоль его окружности, т. е. число вариаций по диаметру и по азимуту.

Аналогичный анализ можно провести и для Е – волн, в этом случае условие распространения поля определяется

при , ,

где - n – ый корень функции Бесселя m – го порядка. Как видно из анализа, в круглом волноводе также распространяется бесчисленное множество (континуум) мод, условие распространения которых определяется обращением в нуль функций Бесселя (Е - волны) или их производных (Н - волны), а значения критических частот определяются значениями корней этих функций.

В круглом волноводе основной является волна , при радиусе волновода а она имеет наибольшую критическую длину волны . В этом смысле волна является аналогом волны в прямоугольном волноводе. В таблице 6.1 приведены структуры поля некоторых типов волн и их критические частоты.

Таблица В1

Характеристика	Тип волны
Поле в плоскости поперечного сечения
Компоненты полей, отличные от нуля	, , , ,	, ,	, ,

Особый интерес представляет в круглом волноводе волна . Затухание этой волны с ростом частоты, в отличие от других волн, уменьшается (рис. 6.5).

Это объясняется следующим образом. Все типы волн, кроме , имеют электрическое поле, линии которого замыкаются на стенках волновода, т.е. возникают токи проводимости на стенках, приводящие к тепловым потерям и увеличению затухания, с ростом частоты эти потери возрастают. Силовые линии электрического поля волны циркулируют по поперечным замкнутым окружностям (табл. 6.1) внутри волновода и не соприкасаются со стенками волновода. Этим линиям соответствуют токи смещения в диэлектрике , в металлических стенках токи отсутствуют. С увеличением частоты силовые линии электрического поля концентрируются в центре волновода.

Однако волна не является основной, кроме того, она является неустойчивой, так как линии поля не имеют жесткой связи со стенками волновода. Эта волна чувствительна к различным неоднородностям и деформациям в волноводе и легко трансформируется в другие высшие типы волн.

Для повышения устойчивости этой волны используются не сплошные волноводы, а спиральные, тогда кольцевые токи смещения поддерживаются спиральными токами в стенках волновода. Спиральные волноводы имеют большее затухание, чем сплошные, поэтому на практике в круглых волноводах используются вставки из спиральных волноводов.

Волноводы непосредственно для организаций линий связи не применяются, т. к. они имеют ряд недостатков. Они применяются в антенно – фидерных трактах в радиорелейной связи, в наземных станциях спутниковых систем связи.

Вопросы для самоконтроля

1. Какие классы и типы волн (моды) распространяются между двумя проводящими плоскостями?

2. Объясните смысл уравнения 6.4.

3. Объясните смысл граничных условий для составляющих поля.

4. Что такое критическая частота (длина волны)?

5. Чем определяется в системе из проводящих бесконечных плоскостей?

6. Охарактеризуйте режим передачи в системе из плоско – параллельных плоскостей?

7. Объясните смысл уравнений 6.12.

8. Какие классы и типы волн распространяются в волноводах?

9. Чем определяется критическая частота (длина волны) в волноводе?

10. Объясните смысл индексов m и n.

11. Объясните смысл уравнения 6.20.

12. Каким условиям удовлетворяет распространение электрических и магнитных волн в круглом волноводе.?

13. Какой основной тип волны в круглом волноводе?

14. Объясните особенности волны в круглом волноводе.

15. Объясните особенности спиральных волноводов.

Письменные задания

1. Определите критические длины волн , для прямоугольного волновода.

2. Приведите структуру поля волны в прямоугольном волноводе.

3. Определите критические длины волн , , если диаметр волновода равен 4 см.

4. Какой тип волны необходимо возбудить в круглом волноводе, чтобы затухание линии длиной 50 м. при длине волны не превышало дБ.

5. Охарактеризуйте достоинства и недостатки волноводов.