3.1. Функциональное описание коммутационного модуля

3.2. Метод синтеза регулярной структуры МПК с декомпозицией по выходам

3.2.1. Одноканальная декомпозиция МПК

3.2.2. Примеры синтеза МПК

3.3. Метод синтеза регулярной структуры МПК с декомпозицией по входам

3.3.1. Однокаскадная декомпозиция МПК

3.3.2. Многокаскадная декомпозиция МПК

3.3.3. Примеры синтеза МПК

3.1. Функциональное описание коммутационного модуля

Пусть имеем два канала k_i{ S_i,, t_i }и k_j{ S_j,, t_j }. Пространственная коммутация этих каналов:

k_i{ S_i,, t_i } ® k_j{ S_j,, t_j } (4)

в силу ортогональности S и Т имеет смысл, если t_i = t_j . Таким образом, пространственная коммутация цифровых каналов - это коммутация одноименных каналов различных трактов. Другими словами, пространственная коммутация цифровых каналов k_i , k_iÎR(S_i) , и k_j , k_jÎR(S_j) сводится к коммутации цифровых трактов:

R(S_i) ® R (S_j) (5)

в интервале t_i .

Следует отметить, что коммутация цифровых трактов может осуществляться в различных интервалах t_i (i = , где С - мощность тракта), что будет cоответствовать пространственной коммутации цифровых каналов k_i тракта R(S_i) с одноименными по временным интервалам каналами k_j тракта R(S_j).

Построим функциональное описание процесса коммутации. Пусть имеем N входящих и М исходящих цифровых трактов, мощность каждого из которых равна С каналам. Поставим в соответствие каждому тракту логическую переменную: входящему – х_i , исходящему – z_j. Введем обобщенную переменную управления а_ij , определяющую обобщенный адрес коммутируемых трактов. Тогда, если считать, что результатом пространственной коммутации является прохождение сигнала по соединительному тракту от входящего к исходящему каналу, можно z_j рассматривать как функцию пространственной коммутации и представить ее в виде булева уравнения:

z_j = x_i a_ij (6)

j

Если для рассматриваемого коммутационного модуля на M входящих и N походящих трактов выполняется условие полнодоступности, т.е. модуль может осуществлять коммутацию одноименных каналов любого входящего о любым исходящим трактом, то его функционально можно описать системой булевых функций:

GG: {z_i = x_i a_ij , i = , j = } (7)

На основе системы (7) могут быть синтезированы различные структуры коммутационного модуля (рис. 2,а), однако наибольшее распространение получили регулярные структуры, образуемые при декомпозиции по выходам (рис. 2,6)

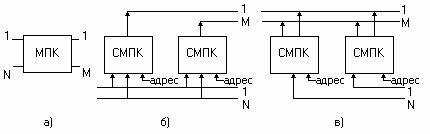и декомпозиции по входам - (рис. 2,в), На рис. 2 приняты следующие обозначения: МПК-модуль пространственной коммутации, СМПК - субмодуль пространственной коммутации. Рассмотрим синтез этих структур.

3.2. Метод синтеза регулярной структуры МПК с декомпозицией по выходам

3.2.1. Одноканальная декомпозиция МПК

В этом случае множество булевых функций с разбивается на подмножества G_j , j = , так что в подмножество G_j входят только те функции Z _{j ,} которые помечены одноименным индексом J , т.е.

G_j : Z _j =X_j a_{i j} , j = , (8)

При этом поскольку коммутационный модуль обладает свойством полнодоступности , то, следовательно, подмножество G_j определяет компоненты обобщенной функции, соответствующей исходящему тракту:

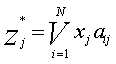
Это справедливо для любого тракта, следовательно, коммутационный модуль можно описать системой H:

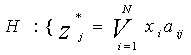, j =

При декомпозиции по выходам переменная выступает в каждом СМПК в виде адреса входа (входящего тракта). Однако фактически при синтезе ШЛК этот адрес должен быть представлен совокупностью адресных переменных, значения которых определяются в результате кодарования. Обозначим через а^αk переменные кодирования, где k=, α ª {0,1}, , , тогда (10) можно переписать в виде

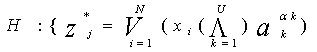, j =

Следует иметь в виду, что при кодировании адреса возможны различные подходы: общее кодирование по всему множеству M x N либо раздельное. В настоящее время получило распространение раздельное Кодирование с ограничением, что обусловлено технологическими особенностями реализации управления коммутационным модулем. Поэтому для этого случая джина адреса U определяется как:

Реализация МПК при декомпозиции по выходам наиболее эффективна при использовании мультиплексоров - избирательных схем типа N*1, осуществляющих коммутацию различных входных сигналов на один выход в соответствии с поступающим адресом. Мультиплексор в общем случае реализует функцию вида

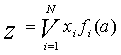
где Z - выходная переменная, соответствующая выходу мультиплексора;

x_i - входная переменная (вход мультиплексора);

f_i (a) - функция адреса i -го входа.

Функция f_i(a) представляет собой конъюнкцию адресных переменных а_i,…,а_k, дополняеляую иногда инверсией переменной S, соответствующей сигналу стробирования:

f_i(a) = a₁^α1 … a_k^αk, α_jÎ{0,1}, j= (14)

Сопоставляя (13) и (II), видим их полную функциональную идентичность. Таким образом, универсальный элемент мультиплексор можно использовать для реализации МПК.

На рис. 3 приведена реализация МПК 16x16 на мультиплексорах К155КП1. Как видим, каждый мультиплексор реализует функцию

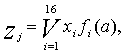
где

f_i(a) =

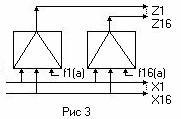Полученная структура МПК называется однокаскадной, поскольку каждая функция реализуется одним мультиплексором. Такая структура получается в v том случае, когда число входящих трактов МПК N не превышает числа входов мультиплексора. Многокаскадная декомпозиция МПК

Если это условие не выполняется, то осуществляется многокаскадная декомпозиция МПК. Вернемся к функции МПК:

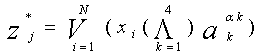
Пусть имеется в распоряжении один тип мультиплексора с параметрами (n ,r ), где n - число его информационных, г- адресных входов. Тогда при определении числа необходимых каскадов следует исходить из соотношения n^q-1≤N≤n^q или преминительно к адресу (q-1)r≤k≤qr.

Конъюнкция адресных переменных в (15) примет в этом случае вид

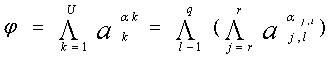
Результирующая функция выхода z_j образуется как композиция функций отдельных каскадов: z_j=F₁* F₂*… F_q, где

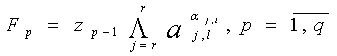
Таким образом, результирующая функция выхода для одного субмодуля МПК примет вид

Если в распоряжении проектировщика оказывается набор различных мультиплексоров, то решается задача оптимизации числа каскадов и числа элементов для их покрытия. Эта задача относится к классической задаче минимизации булевых функций.

3.2.2. Примеры синтеза МПК

Рассмотрим пример синтеза МПК с параметрами N = 40, М = 40. При декомпозиции по выходам имеем функциональное описание:

{z_j = x₁a_1j x₂a_2j …. x₄₀a_40j j = 1,40 }

Определим длину адресной конъюнкции a_ij, имея в виду различное кодирование: u = ] log₂ 40 [ = 6

Пусть требуется реализовать этот МПК на мультиплексорах типа К155КП1 с параметрами n =16, г = 4. Сначала определим необходимое число каскадов q :

16^q-1≤40≤16^q → q = 2

Строим разбиение функций F_p . Дяя этого сначала определим p :

x = {x₁,….,x_p} = ][=][ = 3

Разбиваем множество входных переменных x = {x₁,…,x₄₀} на подмножества мощности не выше n = 16:

x₁ = {x₁,…,x₁₆}

x₂ = {x₁₇,…,x₃₂}

x₃ = {x₃₃,…,x₄₀}

Теперь записываем функции F_p , р = {I, 2, 3}:

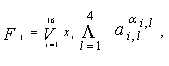
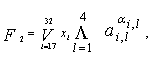
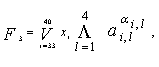
Строим композицию функций выхода одного субмодуля:

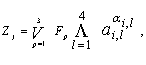
На основе полученной функция cтроим реализацию МПК, как показано на. рис. 4.

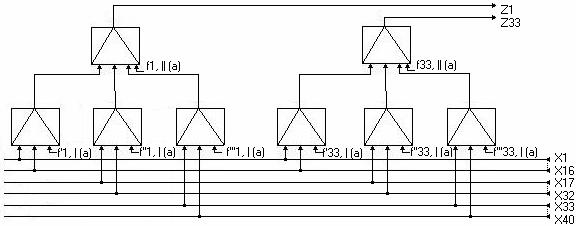В табл.2 приведены некоторые типы мультиплексоров, которые могут быть использованы для построения МПК. Таблица 2

Тип мультеплексора	Число коммутир. входов	Число адресных входов
К155КП1	16	4
К555КП12 К531КП2 КМ155КП2	4x2	2
К155КП5 К5551П15 КМ155КП5	8	3
К1551П7 K56IKП2 КМ155КП7	8	3

3.3. Метод синтеза регулярной структуры МПК с декомпозицией по входам

3.3.1. Однокаскадная декомпозиция МПК

В этом случае множество булевых функций G разбивается на подмножества

B_i , i =, так, что в подмножество В_i входят только те функции z_i , которые содержат входящую переменную x_i

В_i : {z_j = x_i a_ij , j = } (19)

Ради удобства промаркируем функции этого множества индексом i:

В_i : { = x_i a_ij } (20)

Теперь можно построить композицию каждой функции выхода МПК:

z_i : { _* *….*= , j = } (21)

Таким образом каждое подмножество функций В₁ определяет субмодуль с одним входящим трактом x_i и всеми исходящими трактами z_j , j = . Композиция (21) обеспечивает свойство полнодоступности модуля за счет объединения одноименных выходов разных субмоделей (см. рис. 2,в). Процедура синтеза при декомпозиции по входам аналогична рассмотренной выше. Здесь также используется раздельное кодирование и каждая функция подмножества В_i раскрывается в виде:

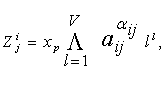(22)

где

(23)

Реализация МПК при декомпозиции по входам наиболее эффективна на

демультиплексорах. Это избирательная схема 1m с одним входом, сигналы c которого могут переключаться на один из m выходов в соответствии с поступающим адресом. Обозначим через х_i - вход, z₁,…,z_m – выходы, f_j(a)- адрес

j-го выхода, тогда функционирование демультиплексора можно описать системами булевых функций

Pi , i =

Pi : {z_j = x_i f_j (a)} , j = (24)

Сопоставляя (22) и (24), можно видеть, что выражения функционально идентичны. Следовательно, универсальный элемент демультиплексор можно использовать для синтеза МПК.

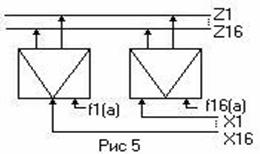На рис. 5 приведена реализация МПК на демультиплексорах. Как видим, каждый демультиплексор реализует функции соответственно:

z₁ = x₁ f₁(a), z ₂= x₂ f₂(a)

z3 = x₃ f₃(a), z ₄= x₄ f₄(a)

где

f_i(a) =

Полученная структура называется однокаскадной, поскольку каждый субмодуль реализуется одним домультиплексором.

3.3.2. Многокаскадная декомпозиция МПК

Однако так же, как в случае декомпозиции по выходам, возможны ситуации, когда число исходящих трактов модуля больше числа коммутируемых выходов демультиплексора. В этом случав осуществляется многокаскадная декомпозиция МПК. Подход к ее осуществлению аналогичен выщерассмотренному, т.е. сначала определяется необходимое число каскадов q , исходя из соотношения М и m :

q = ][

В соответствии о полученным числом каскадов определяется разбиение множества выходов по множеству демультиплексоров. Затем строится композиция выходных функций и соответственно выходов на каждом каскаде.

3.3.3. Примеры синтеза МПК

Рассмотрим пример синтеза MПK с параметрами N = 40, М = 46. При декомпозиции по выходам имеем функциональное описание МПК в виде:

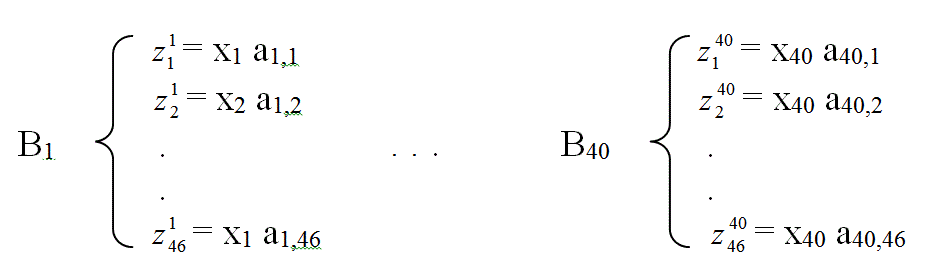
Определяем длину адресной конъюнкции a_ij : v =]log₂46[=6

Пусть требуется реализовать этот МПК на демультиплексорах типа К155ИД3 с параметрами m = 16, r = 4. Сначала определяем число каскадов q :

q = ][=][=3

Затем cтроим разбиение множества выходов z = {z₁, ... , z₄₆} на подмножества мощностью не выше m = 16: Z₁ = {z₁ ,... , z₁₆}, Z₂ = {z₁₇ ,... , z₃₂}, Z₃ = {z₃₃ ,... , z₄₆}.

Теперь расписываем функции по каскадам: Z₁ - первый каскад, Z₂ - второй каскад, Z₃ - третий каскад.

Строим композицию функций одного субмодуля МПК:

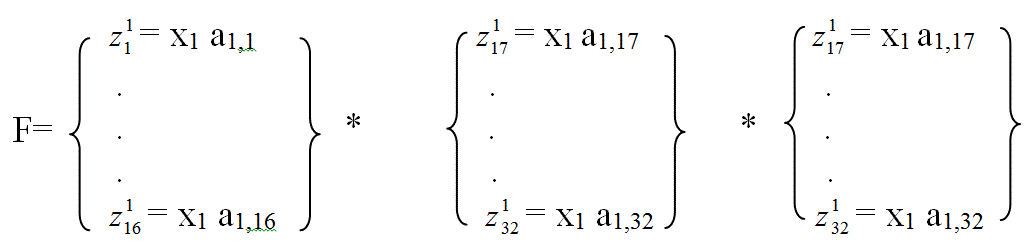
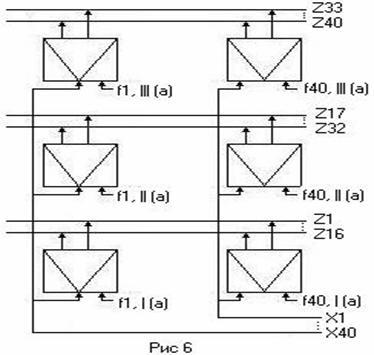
На основе полученной композиции строим реализацию МПК, как показано на рис. 6.

В табл. 3 приведены некоторые типы демультиплексоров, которые можно использовать для синтеза МПК.

Таблица 3

Тип демультиплексора	Число коммутир. выходов	Число адрес, входов	Строб.
К155ИДЗ К155ИД4	16 2х4	4 2	есть есть

Здесь мы рассмотрели проблему синтеза МПК с точки зрения реализации процесса коммутации, не касаясь проблем управления коммутацией, т.е. адресации и распределения. Это сложная проблема, которая требует отдельного рассмотрения.