Уравнения передачи в матричной форме. Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности, для системы уравнений в Y-параметрах (12.2)
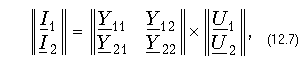
где слева и справа записаны матрицы-столбцы.
Действительно, выполняя операцию умножения в правой части (12.7), имеем
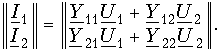
Из равенства этих матриц следует система уравнений (12.2). Система уравнений в Z-параметрах в матричной форме записи имеет вид:
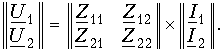
Для уравнений передачи в апараметрах
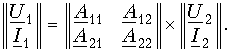
Наконец, запишем в матричной форме системы уравнений передачи в нпараметрах и F-параметрах:
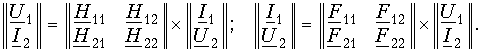
Расчет соединений четырехполюсников. Сложные четырехполюсники можно представить в виде различных соединений простых четырехполюсников. При этом параметры сложного четырехполюсника могут быть найдены по параметрам образующих его простых четырехполюсников.
На рис. 12.4 показана схема каскадного соединения двух четырехполюсников. В соответствии с обозначениями на рисунке при каскадном соединении U2'=U1'' I2'=I1''. Для каждого из четырехполюсников можно составить матричные равенства:
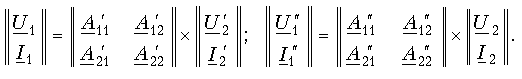
Так как матрицы
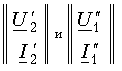
равны между собой, получаем для результирующего четырехполюсника.
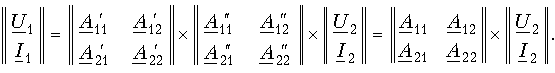
Таким образом, матрица А результирующего четырехполюсника при каскадном соединении равна произведению одноименных матриц соединенных четырехполюсников: А = А'А''. Это правило распространяется на любое число каскадно соединенных четырехполюсников, причем матрицы должны записываться в порядке следования четырехполюсников, так как умножение матриц не подчиняется переместительному закону.
При последовательном соединении двух (или большего числа) четырехполюсников (рис. 12.5) удобно пользоваться матрицами Z. Для этого вида соединения и , т. е. напряжения на выходах и входах отдельных четырехполюсников в результирующем четырехполюснике складываются. Записывая уравнения передачи в Z-форме для каждого четырехполюсника
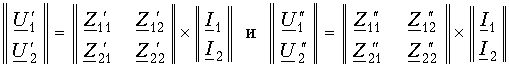
и складывая эти матричные равенства, получаем
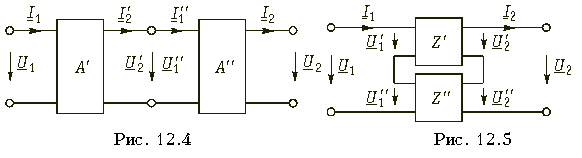
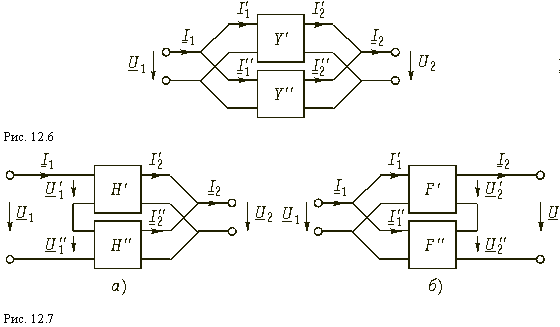
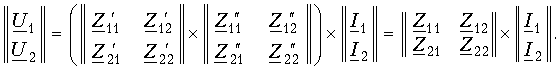
При последовательном соединении четырехполюсников матрица Z результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников: Z = Z' + Z''.
Совершенно аналогично доказывается, что при параллельном соединении четырехполюсников (рис. 12.6), где и , матрица Y результирующего четырехполюсника равна сумме одноименных матриц соединяемых четырехполюсников: Y = Y' + Y''.
Матрицы Н удобно применять при смешанном - последовательнопараллельном соединении четырехполюсников (рис. 12.7, а). При этом H = H' + H''.
Матрицы F удобно применять при параллельнопоследовательном соединении четырехполюсников (рис. 12.7, б). При этом F = = F' + F''.
Параметры типовых четырехполюсников. К типовым пассивным четырехполюсникам относят г, т, побразные схемы (см. рис. 12.2, бг), мостовые (см. рис. 12.2, а) и тперекрытые схемы (см. рис. 12.2, д). Можно получить, основываясь на матричных методах расчета, параметры типовых четырехполюсников, если рассматривать их как сложные четырехполюсники, состоящие из соединений простейших четырехполюсников.
Рассмотрим сначала простейшие четырехполюсники, изображенные на рис. 12.8, а и б. Для первого из них (рис. 12.8, а), пользуясь законами Кирхгофа, можно записать: U1 = U2 + I2Z1 и
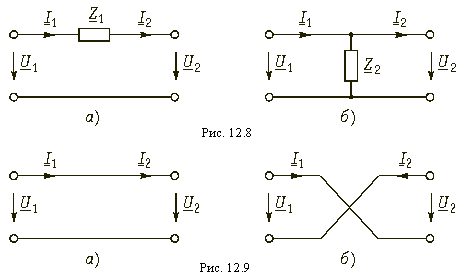
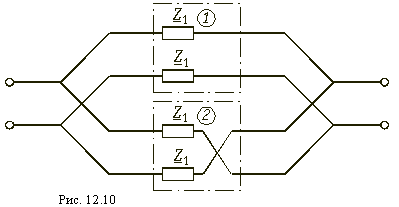
I1 = I2. Сравнивая эти уравнения с уравнениями в апараметрах (12.4), можно записать матрицу А для такого четырехполюсника:
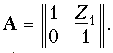
Для второго простейшего четырехполюсника (рис. 12.8, б) имеем U1 = U2 и I1 = U2/Z2 + I2 и поэтому
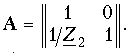
Другие матрицы - Z, Y и Н - могут быть легко получены из табл. 12.1. Заметим, что для первого простейшего четырехполюсника не существует Z-параметров, так как все они обращаются в бесконечность. По этой же причине для второго простейшего четырехполюсника не существует Y-параметров.
На рис. 12.9, а, б показаны соответственно прямое и скрещенное соединения. Нетрудно убедиться, что прямому соединению соответствует матрица
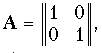
а скрещенному соединению - матрица
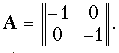
Найдем теперь параметры типовых пассивных четырехполюсников, изображенных на рис. 12.2. гобразный четырехполюсник (рис. 12.2, б) получается путем каскадного соединения простейших четырехполюсников, приведенных на рис. 12.8, а и б. Его матрица
А может быть получена перемножением вышеприведенных матриц простейших четырехполюсников:
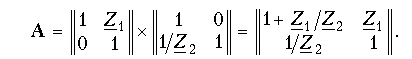
Для тобразного четырехполюсника (рис. 12.2, в) матрицу А можно найти, если рассматривать его как каскадное соединение гобразной схемы с элементами Z1 и Z2 и простейшей схемы с элементом Z3 в продольном плече (рис. 12.8, а):
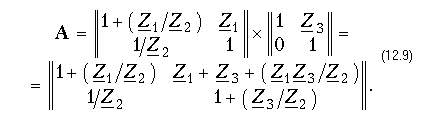
Для побразной схемы (рис. 12.2, г), если ее представить в виде каскадного соединения простейшего четырехполюсника, изображенного на рис. 12.8, б и гобразного четырехполюсника с элементами Z2 в продольном плече и Z3 в поперечном плече, матрица
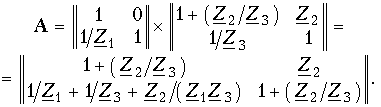
Зная апараметры г, т и побразных четырехполюсников, можно найти по табл. 12.1 другие системы параметровкоэффициентов.
Мостовой четырехполюсник (см. рис. 12.2, а) можно представить как параллельное соединение двух простейших четырехполюсников (рис. 12.10). При параллельном соединении следует пользоваться матрицами Y. Используя данные табл. 12.1, найдем по известным матрицам А простейших четырехполюсников (второй из них имеет скрещенные выходные зажимы) их матрицы Y и, просуммировав последние, получим результирующую матрицу Y мостового четырехполюсника. Матрицы Y простейших четырехполюсников с учетом скрещивания выходных зажимов во втором равны
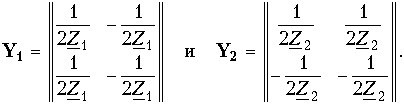
Отсюда матрица Y мостовой схемы
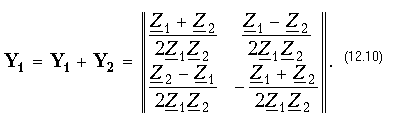
С помощью табл. 12.1 можно получить матрицы А и Z мостового четырехполюсника:
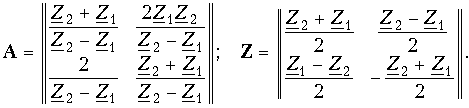
Предлагаем читателям самостоятельно найти параметры тперекрытого четырехполюсника (см. рис. 12.2, д), рассматривая его как параллельное соединение простейшего четырехполюсника с сопротивлением Z4 в продольном плече и тобразного четырехполюсника.
Параметры зависимых источников. Системе уравнений в Y-параметрах (12.2, б) можно сопоставить в соответствии с ЗТК схему с двумя зависимыми источниками типа ИТУН (рис. 12.11, а). Если положить Y11 = Y12 = Y22 = 0 и Y21 = НY, то получим идеальный источник тока, управляемый напряжением (рис. 1.7, б). Таким образом, Y-матрица идеального ИТУНа равна

Воспользовавшись таблицей 12.1, можно записать его а-матрицу:
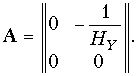
Аналогичным образом системе уравнений (12.5) в нпараметрах можно сопоставить согласно ЗНК схему с двумя зависимыми источниками: ИНУН и ИТУН (рис. 12.11, б). Принимая Н11 = = Н12 = Н22 = 0 и Н21 = Нi переходим к идеальному источнику тока, управляемому током (рис. 1.7, г). Его матрица Н имеет вид
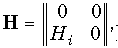
а переход с помощью таблицы 12.1 к аматрице дает
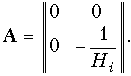
Если использовать систему уравнений (12.3) в Z-параметрах, то получаем схему с двумя источниками типа ИНУТ (рис. 12.11, в). Полагая Z11 = Z12 = Z22 = 0 и Z21 = НZ, приходим к идеальному источнику напряжения, управляемому током (рис. 1.7, в). Значит Z-матрица идеального ИНУТ записывается в виде
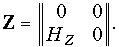
Соответствующая ей а-матрица равна
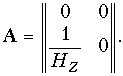
Система уравнений четырехполюсника в F-параметрах (12.5) связывает входной ток I1 и выходное напряжение U2 с остальными двумя величинами U1 и I2:
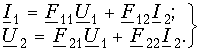
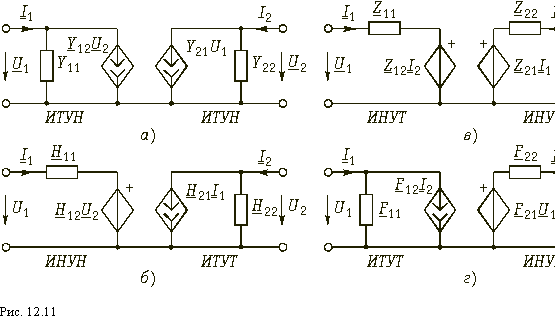
Она может быть представлена схемой, показанной на рис. 12.11, г. При F11 = F12 = F22 = 0 и F21 = Нu данная схема превращается в идеальный ИНУН (рис. 1.7, а). Следовательно, F-матрица ИНУН записывается в виде:
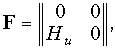
и соответствующая ей а-матрица:
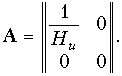
К числу простейших активных линейных четырехполюсников с зависимыми источниками относятся транзисторы и лампы, работающие в линейном режиме.
Чаще всего для транзисторов используют уравнения передачи в н или Y-параметрах. Иногда используются также Z-параметры. Усредненные значения Y-, Z- и нпараметров транзисторов приводятся в справочной литературе. Следует иметь в виду, что одни и те же параметры имеют различные значения в зависимости от того, какой именно из электродов транзистора (эмиттер, база, коллектор) является общим для входной и выходной пар зажимов транзистора как четырехполюсника. Различают поэтому Y-, Z- и нпараметры транзисторов с общим эмиттером, с общей базой и с общим коллектором.
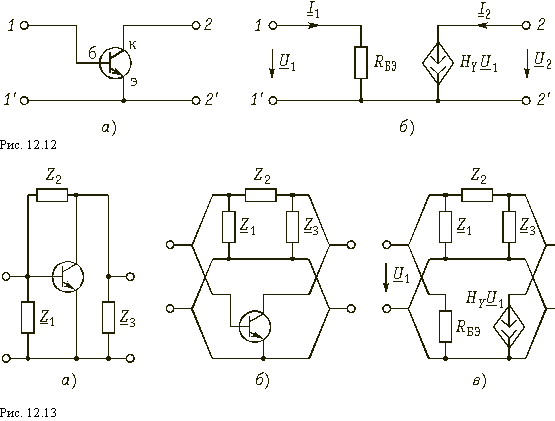
Пример. Определим параметры биполярного транзистора прп типа, включенного по схеме с общим эмиттером (рис. 12.12, а). Его схема замещения в области нижних частот показана на рис. 12.12, б. Сравнивая эту схему со схемой рис. 12.11, а, видим, что при Y11 = 1/RБЭ, Y12 = 0, Y21 = HY и Y22 = 0 обе схемы становятся идентичными. Следовательно, Y-матрица биполярного транзистора с общим эмиттером имеет вид
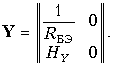
По формулам табл. 9.1 находим матрицы А и Н транзистора:
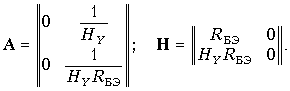
Электронная лампа как четырехполюсник чаще всего характеризуется Y- или апараметрами. Для электронной лампы с общим катодом, если считать, что сеточные токи отсутствуют, и не учитывать паразитные емкости, имеем:
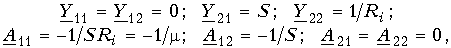
где S - крутизна электронной лампы (скорость изменения анодного тока с изменением сеточного напряжения); Ri - внутреннее сопротивление лампы; m - коэффициент усиления лампы.
При перечисленных выше условиях Z- и нпараметров для электронной лампы не существует. В общем случае, когда с влиянием между электродами лампы через паразитные элементы приходится считаться, ни один из параметров лампы с учетом ее паразитных элементов не равен нулю и лампа как четырехполюсник может характеризоваться любой системой параметров.
Параметры сложных четырехполюсников. При анализе сложного четырехполюсника следует выделить простейшие и типовые четырехполюсники и установить способы их соединения. Затем с помощью матричных методов расчета можно определить соответствующие матрицы сложного четырехполюсника.
Пример. Рассмотрим методику определения нпараметров каскада усилителя на транзисторе со схемой, показанной на рис. 12.13, а. Каскад усилителя образуется в результате параллельного соединения транзистора и побразного пассивного четырехполюсника (рис. 12.13, б). Поэтому следует оперировать матрицами Y соединяемых четырехполюсников. Ранее для побразной схемы была найдена матрица А. От нее с помощью табл. 12.1 можно перейти к матрице Y побразного четырехполюсника. Для транзистора, включенного по схеме с общим эмиттером, Y-параметры определяем из выбранной модели (рис. 12.13, в), либо берем из справочника. Просуммировав найденные таким образом матрицы Y побразного четырехполюсника и транзистора, получим матрицу Y усилительного каскада. Далее по табл. 12.1 перейдем к искомой матрице Н усилительного каскада.

