В дискретной системе связи при отсутствии помех информация на выходе канала связи (канала ПИ) полностью совпадает с информацией на его входе, поэтому скорость передачи информации численно равна производительности источника сообщений:

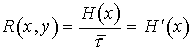. (21)

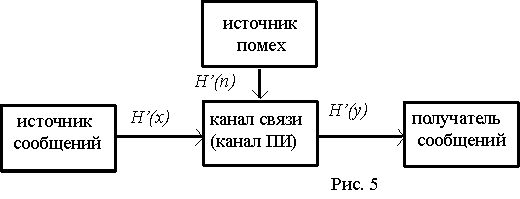
При наличии помех часть информации источника теряется и скорость передачи информации оказывается меньшей, чем производительность источника. Одновременно в сообщение на выходе канала добавляется информация о помехах (рис.5).

Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию:

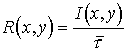бит/с. (22)

На основании формулы (20) имеем

или

, (23)

где H¢(x) - производительность источника;

H¢(x/y) - "ненадёжность" канала(потери) в единицу времени;

H¢(y) - энтропия выходного сообщения в единицу времени;

H¢(y/x)=H’(n) –энтропия помех ( шума) в единицу времени.

Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по каналу

. (24)

Для достижения максимума учитываются все возможные источники на выходе и все возможные способы кодирования.

Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согласованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.

В канале без помех C=max H¢(x), так как H¢(x/y)=0. При использовании равномерного кода с основанием k, состоящего из n элементов длительностью tэ, в канале без помех

,

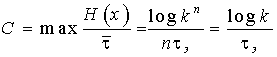при k=2 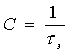бит/c. (25)

Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов связи без помех, так и для каналов с помехами на основании двух теорем, доказанных К.Шенноном.

1-ая теорема (для канала связи без помех):

Если источник сообщений имеет энтропию H (бит на символ), а канал связи – пропускную способность C (бит в секунду), то можно закодировать сообщения таким образом, чтобы передавать информацию по каналу со средней скоростью, сколь угодно близкой к величине C, но не превзойти её.

К.Шеннон предложил и метод такого кодирования, который получил название статистического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмена и в настоящее время широко используется на практике для “cжатия сообщений”.

2-ая теорема (для каналов связи с помехами):

Если пропускная способность канала равна C, а производительность источника H’(x)<C, то путём соответствующего кодирования можно передавать информацию по каналу связи со скоростью, сколь угодно к C и с вероятностью ошибки, сколь угодно близкой к нулю. Если же H’(x)>C, то можно закодировать источник таким образом, что ненадёжность будет меньше, чем H’(x)-C+e, где e. – сколь угодно малая величина.

Не существует способа кодирования, обеспечивающего ненадёжность, меньшую, чем H'(x)-C.

К сожалению, теорема К.Шеннона для каналов с шумами(помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако известно, что при приближении к пределу, устанавливаемому теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах кодирования и декодирования из-за увеличения длины кодового слова n. При этом вероятность ошибки на выходе канала стремится к величине

. (26)

Cледовательно, имеет место “обмен” верности передачи на скорость и задержку передачи.

Вопросы

1. Что такое пропускная способность канала связи, как она определяется?
2. Чему равна пропускная способность канала связи без помех?
3. Как влияют помехи на величину пропускной способности?
4. Что утверждает теорема Шеннона для канала связи без помех?
5. Что утверждает теорема Шеннона для канала связи с помехами?