8.4.1. Алгоритм формирования скремблированного линейного сигнала
8.4.2. Алгоритмы формирования линейных сигналов в классе кодов 1В2В
8.4.3. Алгоритмы формирования линейных сигналов в классе кодов nBmB
8.4.1. Алгоритм формирования скремблированного линейного сигнала
Скремблирование осуществляют с помощью устройства, реализующего логическую операцию суммирования по модулю два исходной двоичной последовательности и преобразующего случайного сигнала, в качестве которого используется псевдослучайная последовательность (рисунок 8.7).
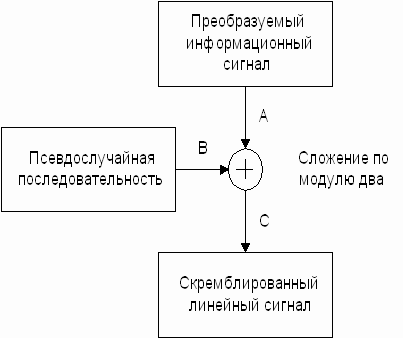
Рисунок 8.7. Схема формирования скремблированного линейного сигнала
Операция сложения по модулю два заключается в следующем:
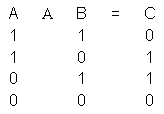
Псевдослучайная последовательность для линейного кодирования в ВОСП формируется циклически, например, линейный код SDH систем воспроизводится за 127 тактов. Для формирования линейного скремблированного кода в формате NRZ генерируется образующий полином по схеме
g(x) = 1 + x 6 + x 7, (8.4)
где x n обозначает единицу в n – м разряде, т.е. в разрядах 6 и 7. Общая длина скремблирующей последовательности равна 7.
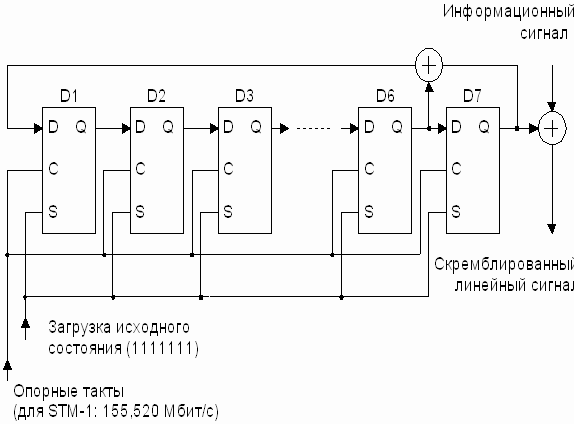
Рисунок 8.8. Схема формирования скремблирующей последовательности
Схема формирования скремблирующей последовательности представлена на рисунке 8.8.
Псевдослучайную последовательность формируют семь D-триггеров и сумматор по модулю два. Каждым опорным тактам цифровые данные перемещаются из триггера в триггер. Благодаря сумматору по модулю два образуется псевдослучайный код (рисунок 8.9).
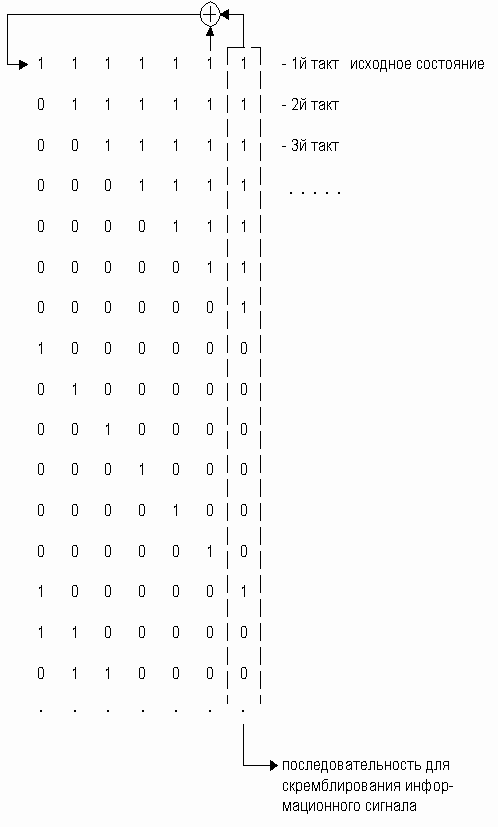
Рисунок 8.9. Формирование псевдослучайного скремблирующего кода
После скремблирования происходит формирование линейного сигнала в формате NRZ (рисунок 8.10).
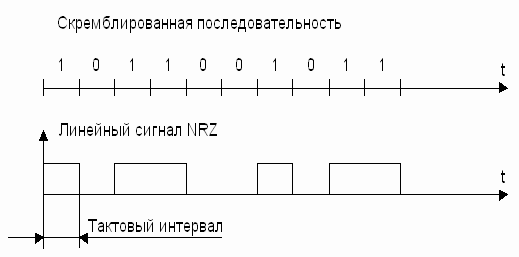
Рисунок 8.10. Формирование линейного сигнала в формате NRZ
При скремблировании линейного сигнала системы SDH группа двоичных символов, расположенная в начале цикла STM-N не подвергается преобразованию в скремблере. Эта группа символов (6 байт´ N) образует синхрослово, которое необходимо для распознавания цикла STM-N на приемной стороне. Обнаружение цикла STM-N в приемной части позволяет запустить процедуру дескремблирования и восстанавливать информационный сигнал из линейного.
Основные достоинства скремблированного линейного сигнала ВОСП:
- стабильность скорости передачи по линии;
- остаточно точное выделение тактовой частоты для регенерации;
- уменьшение влияния статистических параметров информационного сигнала на фазовое дрожание цифрового линейного сигнала.
8.4.2. Алгоритмы формирования линейных сигналов в классе кодов 1В2В
Широкое распространение кодов класса 1В2В обусловлено простотой формирования и требуемыми характеристиками. Среди этих кодов наибольшее применение получили:
- BI – L, Biphase – Level – абсолютный биимпульсный;
- DBI, Differential Biphase – дифференциальный бифазный;
- BI – M, BI – S, Biphase Mark and Space – бифазный относительно единицы и нуля;
- CMI, Complemented Mark Inversion – с инверсией групп символов;
- МCMI, модифицированный CMI.
Алгоритмы кодирования для указанных кодов представлены в таблице 8.2.
Таблица 8.2. Таблицы кодирования некоторых видов кода 1В2В
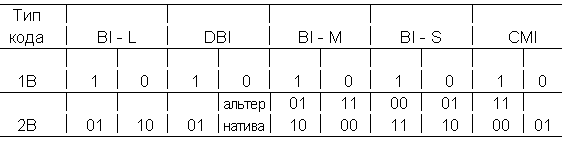
Код МCMI предназначен для преобразования троичного сигнала HDB-3 (High Density Bipolar of Order 3) в биимпульсный по правилу, приведенному в таблице 8.3.
Таблица 8.3

Примеры формирования линейных сигналов ВОСП в кодах класса 1В2В представлены на рисунке 8.11.
К достоинствам линейных кодов класса 1В2В относят малое число последовательностей одинаковых символов, малые размеры схем кодеров/декодеров, хорошую сбалансированность и устойчивый тактовый синхронизм. Недостатком этих кодов можно считать двукратное увеличение скорости передачи и, соответственно, расширение полосы частот сигнала. На рисунке 8.12 приведены спектральные характеристики для сигналов в кодах 1В2В.
Другие характеристики кодов класса 1В2В подробно представлены в [10].
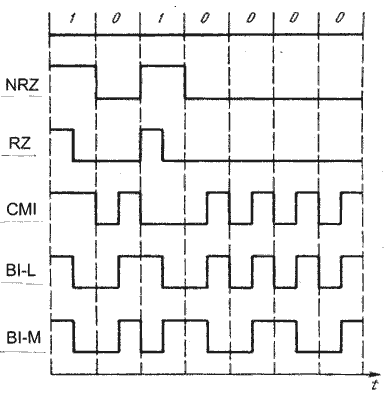
Рисунок 8.11. Примеры формирования линейных сигналов ВОСП в кодах класса 1В2В
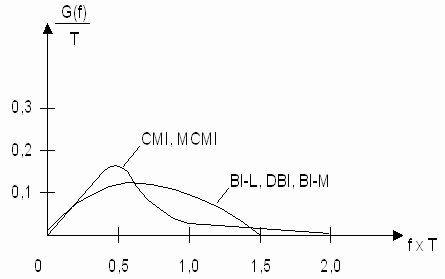
Рисунок 8.12. Энергетические спектры линейных кодов класса 1В2В
8.4.3. Алгоритмы формирования линейных сигналов в классе кодов nBmB
Блочные коды могут быть с постоянной или переменной длиной блоков. В ВОСП используются коды с постоянной длиной блоков, формируемые как nBmB по соответствующим таблицам - алфавитам. Примеры таблиц - алфавитов приведены ниже.
Таблица 8.4. Линейный блочный код 3В4В
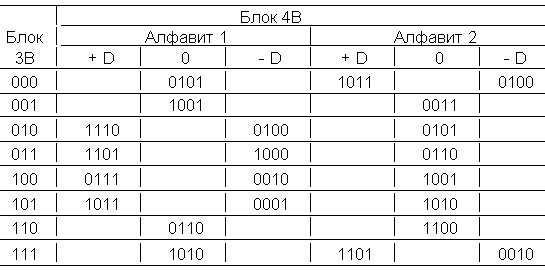
Представленный пример отражает принцип взвешенного кодирования с проверкой на четность и разными алфавитами. При взвешенном кодировании все комбинации из m символов (в примере m = 3) исходного двоичного кода общим числом 2 m (в примере 2 3 = 8) разбивается на две группы. В каждой комбинации каждой группы выбирается n > m (в примере n = m + 1), но таким, что для первой группы n содержит постоянное число единиц с равным весом (в примере диспаритет D = 0 для 0101, 1001, 0110, 1010), а комбинации n второй группы кодируются поочередно в блоки с неравенством единиц и нулей (в примере это 1110 и 0100 различного диспаритета + D и - D соответственно). Кроме того, может выбираться подходящий алфавит. Как видно из таблицы 8.4, некоторые блоки n вообще исключены из алфавитов, например, 0000 и 1111.
Другой пример блочного кодирования представлен на рисунке 8.13.
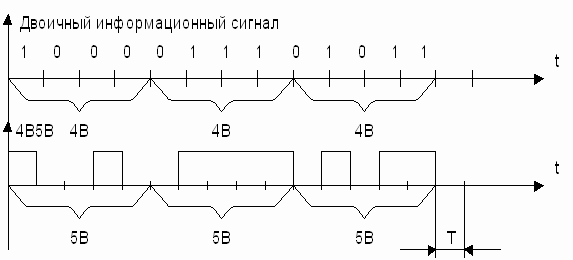
Рисунок 8.13. Сигнал в коде 4В5В – NRZ
Сбалансированное блочное кодирование обеспечивает устойчивый тактовый синхронизм приемника, надежное обнаружение ошибок при подсчете цифровой суммы, увеличение тактовой частоты заметно меньшее, чем при кодировании 1В2В. Энергия непрерывной составляющей сигнала в кодах mBnB сосредоточена в узком спектре частот и не содержит постоянной составляющей. Пример энергетического спектра кода 5В6В приведен на рисунке 8.14.
Алгоритмы формирования сигналов в кодах со вставками изложены выше. Примеры временных диаграмм, отражающих процессы кодирования, рассмотрены в [10]. Характеристики кодов со вставками близки характеристикам кодов mBnB.
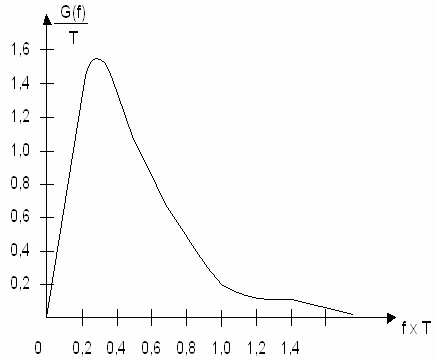
Рисунок 8.14. Спектральная характеристика кода 5В6В
Многоуровневые коды ВОСП пока не получили широкого применения и в предлагаемом учебном пособии не рассматриваются.

