14.1. Токи электрического влияния ближнем и дальнем концах
14.2. Токи магнитного влияния на ближнем и дальнем концах
14.3. Полный ток электромагнитного влияния на ближнем и дальнем концах
14.1. Токи электрического влияния ближнем и дальнем концах
Рассмотрим общий случай, когда две двухпроводные цепи с параллельными проводами имеют различные параметры и замкнуты на концах на согласованные нагрузки (рис. 1).
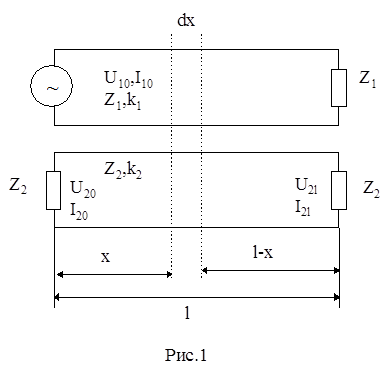
Допущения:
1. Другие цепи отсутствуют;
- цепь 1 - влияющая;
- цепь 2 - подверженная влиянию;
- линии электрически длинные.
2. Цепь 2, подверженная влиянию, собственных источников энергии не имеет.
3. Цепь 1, влияющая, имеет собственный источник энергии.
4. Обозначим напряжения и токи во влияющей цепи U10, I10; на ближнем конце U20, I20 и U2l, I2l на дальнем конце цепи подверженной влиянию.
Напряжение и ток в любой точке цепи 1, расположенной на расстоянии х от её начала при согласованных нагрузках (
) определяются выражениями (уравнение однородной линии):
, (1)
, (2)
, (3)
где 
и 
- соответственно волновое сопротивление и коэффициент распространения.
За счёт электрического влияния в цепи 2 ток на участке dx равен
(4)
Этот ток разветвляется на 2 части. Одна часть направляется к ближнему концу, а другая - к дальнему (рис. 2).
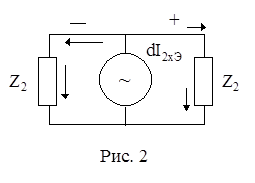
При распространении они будут уменьшаться по амплитуде и изменяться по фазе и через нагрузки на концах цепей пройдут токи одинакового направления.
Допущения: За положительное направление тока примем направление по часовой стрелке, а за отрицательное - против часовой стрелки.
На ближнем конце
, (5)
а на дальнем конце
(6)
Будем полагать, что Y12 = const. Тогда полные точки электрического влияния на ближнем и дальнем концах с учётом формул (1), (2) и (3), равны:
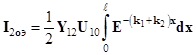, (7)
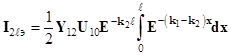, (8)
14.2. Токи магнитного влияния на ближнем и дальнем концах
За счёт магнитного влияния во втором проводе на участке dx, взятом на расстоянии х от начала сближения, индуктируется продольная ЭДС
.
При согласованной нагрузке через отрезок dx во второй цепи ток будет (рис. 3) :
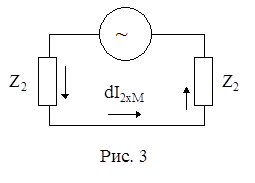
(9)
Ток 
замыкается по цепи последовательно проходя через нагрузки ближнего и дальнего концов в противоположных направлениях (рис. 6). С учётом волновых процессов на ближнем конце:
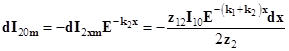(10)
- на дальнем конце
(11)
Полагая Z12 = Const на всей длине сближения цепей, определим полные токи магнитного влияния:
- на ближнем конце
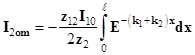; (12)
- на дальнем конце
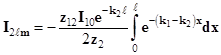. (13)
14.3. Полный ток электромагнитного влияния на ближнем и дальнем концах
Суммарный ток влияния в цепи 2 за счёт электрического и магнитного полей, поступающий к ближнему концу, составит
.
Подставив значения 
и 
из формул (7) и (12), получим
,
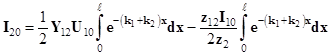и учитывая, что 
, в окончательном виде получим
, (14)
где 
- коэффициент ЭМ связи на ближнем конце.
На дальнем конце: 
. Подставив значения 
и 
из формул (8) и (13), получим
, (15)
где 
- коэффициент ЭМ связи на дальнем конце,
и
имеют размерность см/км.
В полученных уравнениях (14) и (15) величины 
и 
являются характеристиками ЭМ влияния на ближний и дальний концы, поскольку характеризуют отношение токов во влияющей и подверженной влиянию цепях. Поэтому их называют коэффициентом ЭМ связи на ближнем и дальнем концах.
Коэффициент ЭМ связи на ближнем конце:
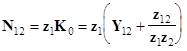. (16)
Коэффициент ЭМ связи на дальнем конце:
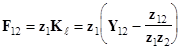. (17)
Коэффициенты 
и 
- безразмерны.
Учитывая (16) и (17) основные уравнения влияния между цепями примут вид:
- на ближнем конце
; (18)
- на дальнем конце
. (19)