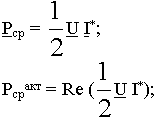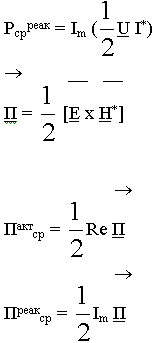5.4. Относительность свойств реальных сред
В основе классификации ЭМП лежат 2 критерия:
- Зависимость полей от времени.
- Соотношение между токами проводимости и смещения.
5.1. Статические поля
Статические поля не зависят от времени :
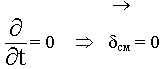
Заряды неподвижные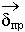 
= 0.
Уравнения Максвелла:
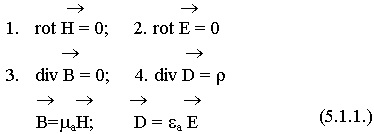
В статических полях электрические и магнитные явления проявляют себя независимо. Уравнения Максвелла распадаются на 2 системы:
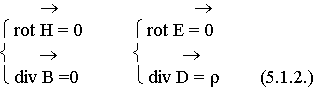
5.2. Стационарные поля
Стационарные поля не зависят от времени 
=0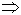 
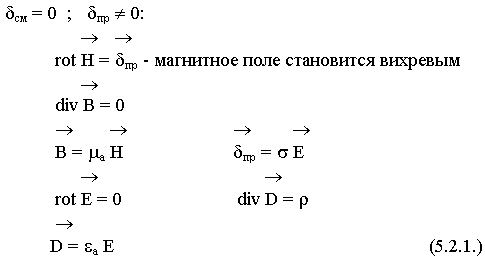
Поля зависят друг от друга. Электрическое поле не вихревое, магнитное вихревое.
5.3. Квазистационарные поля
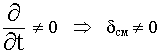Процессы медленно изменяются во времени.
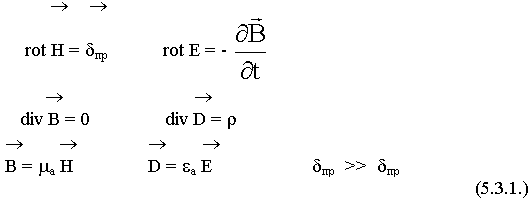
Эти поля детально изучаются в ТЭЦ.
5.4. Относительность свойств реальных сред
В реальных средах существуют токи проводимости и токи смещения. Рассмотрим поведение реальных сред в переменных полях.
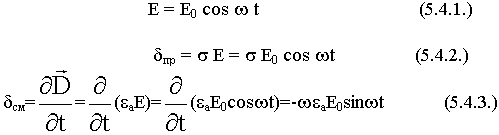
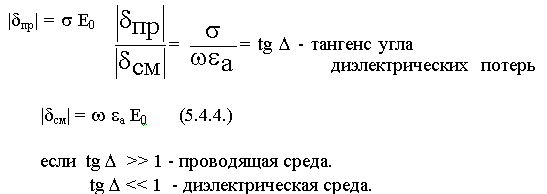
С ростом частоты все среды тяготеют к диэлектрикам.
5.5. Быстропеременные поля
5.5.1. Гармонические процессы и метод комплексных амплитуд
Из-за того, что процесс очень быстро изменяется по времени, то :
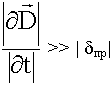(производные по времени большие)
Уравнения Максвелла принимают вид:
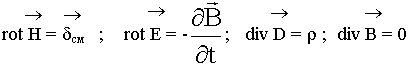(5.5.1.1.)
В дальнейшем в курсе мы будем иметь дело с таким классом полей, т.е. быстропеременным. Из всего многообразия временных зависимостей полей в нашем курсе мы рассмотрим группу, где поля изменяются по гармоническому закону:
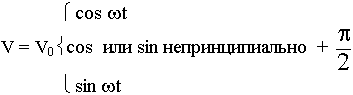
Метод комплексных амплитуд имеет те же предположения, что и в курсе ТЭЦ, мы несколько распространим его на векторные величины.
V = V0 cos w t - в общем виде записана производная векторная величина, изменяющаяся по гармоническому закону.
Как выражается такая величина в методе комплексных амплитуд ?
V = V0 cos w t 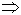V = V0 e j w t - временная зависимость.
Как вернуться к исходному вектору без точки? Какая теорема используется ? Теорема Эйлера.
V = Re V = V0 cos w t
V = V0 cos (w t + j ) 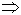V = V0 e j( w t + j) = V0 e jw t
V0 = V0 e j j В этом методе на амплитуду ничего не действует.
Вывод:
- В окончательных выражениях зависимость от времени исчезает, хотя она всегда известна, ее можно восстановить.
- Значительно упрощается дифференцирование и интегрирование по времени, дифференцируем
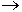умножаем на jw , интегрируем 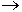делим на jw
= V0 jw e jw t = V jw
Средняя мощность:
5.5.2. Комплексные уравнения Максвелла
Комплексные уравнения Максвелла являются дифференциальной формой законов электромагнетизма для гармонических процессов:
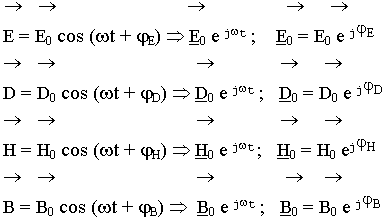(5.5.2.1.)
Применим метод комплексных амплитуд к этому процессу:
= 
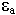
Формально можно записать, хотя деление векторов не встречается.
=
;
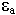где 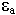- комплексная диэлектрическая проницаемость
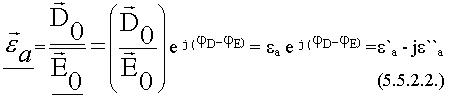
В общем случае фаза, с которой изменяется вектор и вектор могут неравны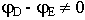 
, т.е. возможно опережение или отставание.
В гармонических полях абсолютная диэлектрическая и магнитная проницаемости величины комплексные:
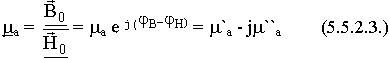
Площадь петли равна энергии на перемагничевание. В любых магнитных материалах имеется запаздывание вектора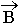 
относительно 
.
Уравнения Максвелла
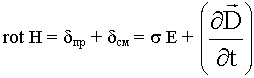- в обычной дифференциальной форме.
Покажем, что уравнения Максвелла относительно временных процессов являются линейными.
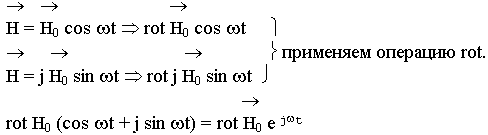
Применим первое уравнение Максвелла к векторным характеристикам полей, записанных в комплексной форме:
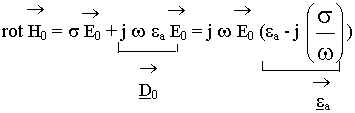(5.5.2.4.)
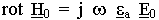в комплексной форме отсутствует зависимость от времени.
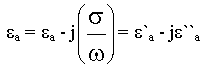
где: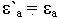 
- характеризует процессы поляризации.
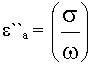- характеризует джоулевые потери.
По аналогии второе уравнение Максвелла:
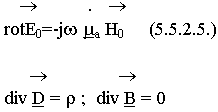
Третье и четвертое уравнения не реагируют на время, не зависят от того, какой процесс гармонический или нет.
Для гармонических процессов третье и четвертое уравнения теряют смысл, они входят в первое и второе.
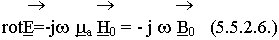
Применим к правой и левой части уравнения (5.5.2.6.) операцию div:
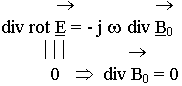
Метод комплексных амплитуд позволил существенно упростить описание полей, т.к. требуется только два уравнения:
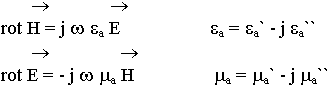
В дальнейшем черточку опускаем, но всегда имеем в виду, что комплексная форма, т.к. присутствует символ j.