Формула Фурье для дискретного сигнала:

– прямое преобразование Фурье.

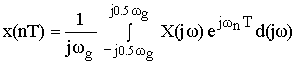– обратное преобразование Фурье.

Сигнал x(nT) нормирован по отношению к X.

После денормирования сигнала формулу записываем в виде:

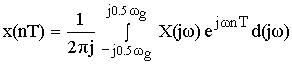
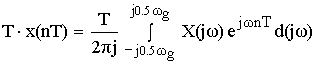
Устремляем T к нулю. Если , то T вырождается в непрерывную переменную

Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов:

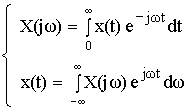
Это доказывает справедливость формулы Фурье для дискретного сигнала. Переменную ω можно распространить на всю плоскость комплексного переменного: , и тогда формулы Фурье для дискретного сигнала заменяются формулами Лапласа.

– прямое преобразование.

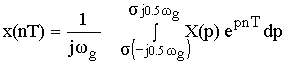– обратное преобразование.