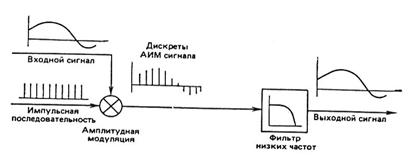
Рис. 7.1. Иллюстрация процедуры дискретизации аналогового сигнала

Под цифровым представлением речевых сигналов (РС) будем понимать их аналого-цифровое преобразование (АЦП). Первый шаг при АЦП РС состоит в его периодической дискретизации - замене непрерывной функции её дискретными значениями. Процесс базируется на теореме отсчетов (теорема В.А. Котельникова), в соответствии с которой произвольный сигнал со спектром, ограниченным некоторой частотой F_в, может быть полностью восстановлен (т.е. преобразован в аналоговую форму с помощью линейной интерполяции) по последовательности своих отсчетов, следующих с интервалом времени Т_д = 1 / (2F_в). Здесь F_в - наивысшая частота спектра (ширина полосы) входного сигнала. Обычно за наивысшую частоту спектра (называемую частотой Найквиста) принимают частоту, ниже которой максимумы спектра имеют уровень не более – 40 дБ. На практике неискаженная передача непрерывного (аналогового) сигнала с полосой частот, ограниченной значением F_в, дискретной последовательностью его отсчетов возможна, если F_д = kF_в, где k>2, а для восстановления используется идеальный фильтр (рис. 7.1). Метод, представленный на этом рисунке, называют обычно амплитудно-импульсной модуляцией (АИМ).

В соответствии с описанием гласных и фрикативных звуков РС не ограничен по полосе частот, хотя его спектр быстро спадает в области высоких частот. На рис. 7.2 изображены спектры типичных звуков речи. Видно, что для вокализованных звуков наивысшая частота, ниже которой максимумы спектра меньше уровня -40 дБ, составляет около 4 кГц. С другой стороны, для невокализованных звуков спектр не затухает даже на частотах выше 8 кГц. Таким образом, для точного воспроизведения всех звуков речи требуется частота дискретизации около 20 кГц. В большинстве приложений такая частота дискретизации, однако, не требуется. Например, если дискретизация предшествует оцениванию трех первых формантных частот вокализованной речи, то достаточно располагать частью спектра до частоты около 3,5 кГц. Следовательно, если перед дискретизацией РС пропускается через ФНЧ так, что F_в = 4 кГц, то частота дискретизации должна составлять 8 кГц.

Этот результат поясняет рис. 7.3, где представлен спектр входного сигнала и результирующий спектр импульсной последовательности АИМ сигнала, состоящий из дискретных гармоник частоты дискретизации. Входной сигнал модулирует каждую из этих гармоник отдельно. В результате этого создаются две боковые полосы около каждой дискретной частоты в спектре импульсной последовательности. ФНЧ, восстанавливающий исходный сигнал, рассчитывается на подавление всех частот, кроме частот исходного сигнала. Как показано на рис.7.3, такой фильтр должен иметь частоту среза, которая расположена между F_в и F_д – F_в. Следовательно, разделение возможно, если выполняется неравенство F_д > 2 F_в.

Входной сигнал перед дискретизацией должен быть ограничен по полосе, чтобы можно было удалить из него составляющие с частотой выше, чем F_д/2, даже если этими составляющими, как неслышимыми, можно было бы пренебречь. Таким образом, полная АИМ-система должна иметь фильтр, ограничивающий полосу сигнала перед дискретизацией, для гарантии того, что никакие ложные или связанные с источником сигналы не приведут к появлению помех в требуемой полосе вследствие наложения спектров после дискретизации. Поэтому этот фильтр часто называют фильтром защиты от перекрытия спектров.

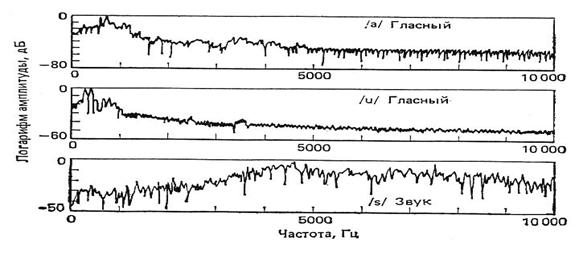
Рис. 7.2. Спектры типичных звуков речи

Второй шаг в процессе АЦП состоит в квантовании, когда непрерывному множеству мгновенных значений отсчетов аналогового сигнала ставят в соответствие конечное множество значений - уровней квантования. Набор разрешенных уровней квантования называется шкалой квантования. Расстояние между разрешенными уровнями - это шаг квантованияD. Разность d между исходным и квантованным сигналами называется ошибкой или шумом квантования. Мощность шумов квантования при наличии сигнала не зависит от сигнала и определяется шагом квантования: Р_ш.кв = D² / 12.

Для передачи квантованные по амплитуде отсчеты преобразуются в двоичные кодовые комбинации - кодовые слова, которые передаются затем в виде потока двоичных импульсов - бит. Эта операция называется кодированием. Необходимое число разрядов для кодирования m при заданном максимальном числе уровней шкалы квантования n_макс определяется из выражения m = log₂n_макс. В цифровых системах связи и вещания распространены двоичные симметричные коды, характеризуемые тем, что первый символ (т.е. старший значащий бит) кодовой комбинации определяется полярностью кодируемого отсчета сигнала, а остальные символы несут информацию об абсолютном значении отсчета.

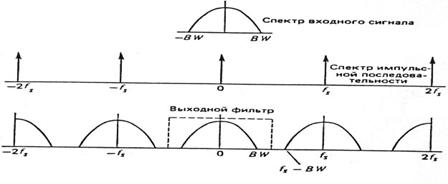
Рис. 7.3. Спектры входного сигнала и импульсной последовательности АИМ сигнала

При цифровой передаче сигналов речи по ТФ каналам общепринятой является F_д = 8 кГц, а число двоичных разрядов АЦП обычно выбирается равным m = 8, включая знаковый разряд. Поэтому диапазон чисел (исключая ноль) на выходе АЦП составляет от -127 до +127. В результате на выходе АЦП формируется последовательность 8-разрядных кодовых слов (т.е. 8-битовых чисел), следующих с частотой 8 кГц. Следовательно, цифровая скорость передачи сигнала на выходе АЦП составляет

R_ц = F_д ´ m = 8 ´ 8 = 64 кбит/с. (7.1)

Эта величина представляет собой информационный объем цифрового представления РС (система ИКМ-64), который необходимо знать при его передаче или хранении.

На приемной стороне линии цифровой передачи в декодере битовый поток восстанавливается и формируются величины квантованных отсчетов. Затем для интерполяции между величинами отсчетов и восстановления исходной формы сигнала используется ФНЧ. Декодер и ФНЧ образуют цифро-аналоговый преобразователь (ЦАП). Если ошибок в передаче не было, то сигнал на выходе идентичен входному - за исключением шума квантования Р_ш.кв. Структурная схема системы ИКМ приведена на рис. 7.4.

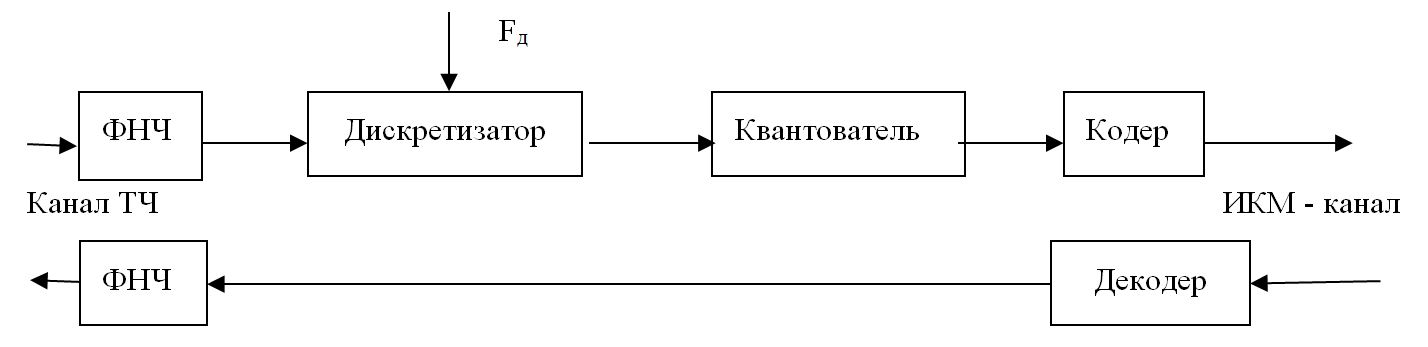
Рис. 7.4. Структурная схема системы ИКМ

Искажения (шум) квантования, возникающие при преобразовании аналогового сигнала в цифровую форму, обычно выражаются в виде отношения средних мощностей сигнала и шума, т.е. отношения сигнал-шум квантования (ОСШК) Р_с/Р_ш.кв. ОСШК, выраженное в децибелах, при равномерном квантовании определяется соотношением:

Р_с / Р_ш.кв = 6m + 4,8 – 20 lg Q, дБ, (7.2)

где Q – значение пик-фактора сигнала. Отсюда имеем:

• для гармонического сигнала (Q = Ö2) Р_с / Р_ш.кв = 6m + 1,8, дБ;
• для речевого сигнала (Q = 12 дБ) Р_с / Р_ш.кв = 6m – 7,2, дБ.

Система ИКМ с линейным квантованием практически не применяется, поскольку для достижения приемлемого качества восприятия восстановленного речевого сигнала при равномерном квантовании необходимо обеспечить m ≥ 12. Столь большое число уровней квантования n_макс = 2¹² при F_д = 8 кГц требует, чтобы скорость R_ц передачи символов в канале была не менее 96 кбит/с. Для существенного уменьшения скорости R_ц цифрового потока прибегают к нелинейному квантованию (рис. 7.5а) в процессе мгновенного компандирования(МК), когда на передающей стороне РС подвергают компрессии по логарифмическому закону, а на приемной осуществляют обратную операцию – экспандирование с помощью экспоненциального преобразования. При МК устраняется психофизическая избыточность, определяемая низкой заметностью искажений квантования на фоне сильного сигнала.

В электросвязи используется ИКМ с компандированием либо по m - закону, либо по А - закону; характеристика компрессии по m - закону приведена на рис. 7.5б для разных значений коэффициента сжатия. Обычно используют m = 30; 100; 255 или А = 87,6. Структурная схема системы ИКМ с МК дополняется элементами логарифмического компандера (рекомендация ITU-T G.711, 1960 г.). Так, можно либо компрессировать исходный сигнал по логарифмическому закону с последующим равномерным квантованием при сравнительно малом числе уровней (например, при m = 8), либо компрессировать предварительно преобразованный в цифровую форму сигнал при сравнительно большом исходном числе уровней квантования (например, при m = 12) с последующим преобразованием к восьмиразрядному коду (m = 8). Результатом преобразования является двоичная последовательность, передаваемая со скоростью R_ц = 64 кбит/с.

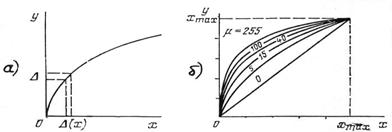
Рис. 7.5. Принцип нелинейного квантования (а) и характеристики компрессии по m - закону (б)

Из-за трудностей реализации неравномерного квантования с аналоговыми компрессорами переходят к цифровым, у которых плавная характеристика компрессии заменяется линейно-ломанной аппроксимирующей функцией с различным числом сегментов.