3. Проектирование реляционных БД. Проектирование реляционных баз данных

: Категория: Проектирование реляционных баз данных

3.1. Функциональные зависимости

3.1.1. Понятие функциональной зависимости

3.1.2. Правила вывода функциональных зависимостей

3.1.3. Неприводимые функциональные зависимости

3.1.4. Диаграммы (схемы) функциональных зависимостей

3.2. Нормализация отношений

3.2.1. Обзор нормальных форм

3.2.2. Декомпозиция без потерь

3.2.3. Первая, вторая и третья нормальные формы

3.2.4. Нормальная форма Бойса-Кодда

3.3. Нормальные формы более высокого порядка

3.3.1. Многозначные зависимости

3.3.2. Четвертая нормальная форма

3.3.3. Зависимость соединения

3.3.4. Пятая нормальная форма

3.4. Итоговая схема процедуры нормализации

3.1. Функциональные зависимости

Проектирование связано с построением логической структуры БД. Иными словами, нужно решить вопрос, какие базовые отношения, с какими атрибутами следует задать.

Суть этой проблемы сводится, в конечном счете, к нормализации отношений.

Сначала рассмотрим основные понятия, необходимые для обсуждения вопросов нормализации отношений.

3.1.1. Понятие функциональной зависимости

Вспомним, что любое отношение рассматривается как переменная, принимающая определенные значения в определенные моменты времени.

Пусть R – переменная отношения, X, Y – произвольные подмножества множества всех атрибутов R. Y функционально зависит от X тогда и только тогда, когда для любого допустимого значения R каждое значение X связано только с одним значением Y.

Обозначается: X→Y

Говорится: «X функционально определяет Y» или «Y функционально зависит от X».

Левая часть выражения называется детерминантом (детерминантой) функциональной зависимости (ФЗ), правая – зависимой частью ФЗ.

Например, в отношении Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Адрес, КодГруппы) существуют такие ФЗ

{№ ЗачетнойКнижки} → {Фамилия, Имя, Отчество}

{№ ЗачетнойКнижки} → {Адрес, КодГруппы}

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, КодГруппы}

Это лишь некоторые ФЗ, из которых можно сделать вывод, что если детерминант содержит первичный ключ, то множество всех остальных атрибутов отношения функционально зависит от него.

Еще пример: в отношении Кафедры (КодКафедры, НазваниеКафедры, Кабинет, Телефон) существуют ФЗ

{КодКафедры} → {Кабинет, Телефон}

{НазваниеКафедры} → {Кабинет, Телефон}

Таким образом, аналогичный вывод можно сделать не только для первичных ключей, но и для альтернативных, то есть для всех потенциальных ключей.

Множество атрибутов отношения, которое содержит в качестве подмножества потенциальный ключ называется суперключом этого отношения.

Рассмотрим еще один пример: если в то же отношение Студенты добавить атрибут СтаростаГруппы, то появятся такие ФЗ:

{КодГруппы} → {СтаростаГруппы}

{СтаростаГруппы} → {КодГруппы}

(причем, ни атрибут КодГруппы, ни атрибут СтаростаГруппы не являются потенциальными ключами)

В этом случае имеется избыточность данных, которая может привести к вводу ошибочных сведений (пользователь случайно может ввести в качестве старосты некоторой группы не того студента, который на самом деле является старостой, но система не выдаст ошибку).

Фактически, если в отношении имеется ФЗ, в которой детерминант не является суперключом, то отношение избыточно.

Существуют такие ФЗ, которые учитываются только формально, т.к. они всегда существуют и подразумеваются самим определением ФЗ. Это тривиальные ФЗ.

Тривиальная функциональная зависимость – это такая ФЗ, зависимая часть которой является подмножеством детерминанта.

Например,

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Фамилия, Имя, Отчество}

{КодГруппы, Курс} → {Курс}

Такие тривиальные ФЗ не рассматриваются при нормализации, но все же они существуют и всегда формально учитываются.

3.1.2. Правила вывода функциональных зависимостей

Из некоторого множества ФЗ конкретного отношения можно получить производные ФЗ.

Например, из ФЗ отношения Студенты

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес, Телефон}

можно получить такие ФЗ:

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес}

{№ ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Телефон}

Пусть S – некое множество ФЗ. Тогда множество всех ФЗ, которые можно получить из S называется замыканием множества S и обозначается S⁺.

Чтобы получить замыкание некоторого множества ФЗ нужны правила вывода ФЗ. Такие правила вывода сформулировал Армстронг (Швеция), поэтому их называют правилами Армстронга (или аксиомами Армстронга).

Обозначим за А, В, С произвольные подмножества множества атрибутов заданного отношения R, а записью АВ будем обозначать объединение А и В.

Правила вывода ФЗ Армстронга:

1) Рефлексивность: если В является подмножеством А, то А → В

2) Дополнение: если А → В, то АС → ВС

3) Транзитивность: если А → В и В → С, то А → С

Каждое из этих правил может быть доказано на основе определения ФЗ, а первое правило – это определение тривиальной ФЗ.

Эти правила полны, т.к. их достаточно для вывода замыкания (т.е. всех ФЗ) начального множества ФЗ.

Они также исчерпывающи, т.к. никакие дополнительные ФЗ не могут быть выведены из начального множества ФЗ.

Но из этих правил для упрощения практического вывода ФЗ можно вывести несколько дополнительных правил (следствий):

4) Самоопределение: А → А

5) Декомпозиция: если А → ВС, то А → В и А → С

6) Объединение: если А → В и А → С, то А → ВС

7) Композиция: если А → В и С → D, то АС → ВD

8) Теорема всеобщего объединения: если А → В и С → D, то А(С-В) → ВD

(названо это правило так, потому что многие другие правила могут быть выведены как частные случаи этой теоремы)

Пример: рассмотрим отношение Группы (КодГруппы, Специальность, Курс,Староста).

В качестве начального множества ФЗ возьмем множество из следующих двух ФЗ:

(1) {КодГруппы} → {Специальность, Курс}

(2) {КодГруппы} → {Староста}

Выведем замыкание этого множества ФЗ.

·По правилу 1 можно записать все тривиальные зависимости:

(3) {Специальность, Курс} → {Специальность}

(4) {Специальность, Курс} → {Курс}

·По правилу 2:

(5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

(6) {КодГруппы, Специальность} → {Староста, Специальность}

(7) {КодГруппы, Курс} → {Староста, Курс}

(8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

·По правилу 3 напрямую ничего не выведем.

·По правилу 4:

(9) {КодГруппы} → {КодГруппы}

(10) {Специальность} → {Специальность}

и т.д. (11), (12)

·По правилу 5:

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

·По правилу 6:

(15) {КодГруппы} → {Специальность, Курс, Староста}

·По правилу 7 напрямую ничего не выведем

·По правилу 8 тоже.

Однако, знание этих правил и умение ими пользоваться не обеспечивают вывода замыкания множества ФЗ, т.к. не существует четкого алгоритма такого вывода.

3.1.3. Неприводимые функциональные зависимости

Функциональная зависимость называется неприводимой слева, если ни один атрибут не может быть опущен из ее детерминанта без нарушения зависимости (иными словами, детерминант неизбыточен).

Например: ФЗ {№ЗачетнойКнижки, Фамилия, Имя, Отчество} → {Адрес} приводима, т.к. из детерминанта можно исключить атрибуты Фамилия, Имя, Отчество без нарушения ФЗ.

А ФЗ {КодГруппы, Дисциплина} → {Преподаватель} отношения Занятия (КодГруппы, Дисциплина, Преподаватель) неприводима, т.к. из детерминанта нельзя исключить ни атрибут КодГруппы, ни атрибут Дисциплина без нарушения зависимости.

Множество ФЗ называется неприводимым тогда и только тогда, когда выполняются три свойства:

1) зависимая часть каждой ФЗ из данного множества содержит только один атрибут;

2) каждая ФЗ из данного множества является неприводимой слева;

3) ни одна ФЗ из данного множества не может быть опущена.

Например, рассмотрим множество ФЗ отношения Группы из примера в предыдущем п.3.1.2.

(1) {КодГруппы} → {Специальность, Курс}

(2) {КодГруппы} → {Староста}

(3) {Специальность, Курс} → {Специальность}

(4) {Специальность, Курс} → {Курс}

(5) {КодГруппы, Староста} → {Специальность, Курс, Староста}

(6) {КодГруппы, Специальность} → {Староста, Специальность}

(7) {КодГруппы, Курс} → {Староста, Курс}

(8) {КодГруппы, Специальность, Курс} → {Староста, Специальность, Курс}

(9) {КодГруппы} → {КодГруппы}

(10) {Специальность} → {Специальность}

(11) {Курс} → {Курс}

(12) {Староста} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

(15) {КодГруппы} → {Специальность, Курс, Староста}

По первому свойству исключаем из этого множества следующие ФЗ: (1), (5), (6), (7), (8), (15).

По второму свойству исключаем следующие ФЗ: (3), (4).

По третьему свойству исключаем: (9), (10), (11), (12).

Остались:

(2) {КодГруппы} → {Староста}

(13) {КодГруппы} → {Специальность}

(14) {КодГруппы} → {Курс}

Полученное множество ФЗ неприводимо. Можно сделать вывод, что полученное множество ФЗ выражает то, что отношение Группы содержит атрибуты КодГруппы, Староста, Специальность, Курс, и КодГруппы – первичный ключ.

3.1.4. Диаграммы (схемы) функциональных зависимостей

Множество неприводимых ФЗ некоторого отношения можно представить в виде диаграммы функциональных зависимостей.

Из таких диаграмм лучше видно, какие ФЗ включить в множество ФЗ, а какие исключить, чтобы оно было неприводимо. Исключить нужно те стрелки (обозначающие ФЗ), которые идут не от потенциального ключа.

Таким образом, с помощью диаграмм можно привести множество ФЗ к неприводимому состоянию.

В качестве примера рассмотрим диаграмму первоначального множества ФЗ из п. 3.1.2.

После того, как лишние стрелки будут убраны, получим диаграмму:

Из нее как раз и следуют перечисленные ранее три оставшиеся ФЗ:

{КодГруппы} → {Курс}

{КодГруппы} → {Специальность}

{КодГруппы} → {Староста}

Таким образом, существует как минимум два способа преобразования множества ФЗ к неприводимому состоянию - путем проверки всех свойств их определения и путем анализа диаграмм ФЗ.

3.2. Нормализация отношений

Вся теория нормализации отношений является не более и не менее как формализацией соображений здравого смысла. Потребность такой формализации в том, чтобы сформулировать общие правила для разработчиков БД, а главное – если такая задача будет полностью выполнена - эти правила могут быть автоматизированы для реализации на ЭВМ.

3.2.1. Обзор нормальных форм

Процесс нормализации отношений основан на концепции нормальных форм (НФ).

Говорят, что отношение находится в некоторой НФ, если оно удовлетворяет заданному набору условий.

Известно несколько НФ (рис. 4).

Из рис. 4 видно, что все условия, необходимые для некоторой НФ, должны выполняться и для всех последующих НФ.

Первые три НФ были определены Коддом, следующая – нормальная форма Бойса-Кодда (НФБК) – Бойсом и Коддом, 4 и 5 НФ были определены Фейгином.

Возникает вопрос, можно ли продолжить нормализацию дальше, получить 6, 7 и т.д. НФ? Действительно, существуют дополнительные НФ, но 5 НФ считается в некотором смысле окончательной. А для практического проектирования достаточной считают 3 НФ.

3.2.2. Декомпозиция без потерь

Нормализация использует операцию декомпозиции. Дело в том, что процедура нормализации предусматривает разбиение отношения на другие, т.е. его декомпозицию. Причем эта декомпозиция должна произойти без потерь информации из первоначального отношения. Можно сказать, что декомпозиция должна быть обратимой.

Например, рассмотрим отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, Адрес, Телефон).

Выполним декомпозицию на два отношения:

Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество) и

Студенты2 (КодГруппы, Адрес, Телефон)

При такой декомпозиции информация утрачивается – для каждой группы будет выведены адрес и телефон только первого по списку студента этой группы. При соединении полученных отношений невозможно восстановить полностью первоначальное отношение.

Выполним декомпозицию по-другому:

Студенты3 (№ЗачетнойКнижки, Фамилия, Имя, Отчество) и

Студенты4 (№ЗачетнойКнижки, Адрес, Телефон)

Вот это – декомпозиция без потерь. Можно соединить полученные два отношения, получив первоначальное.

По своей сути декомпозиция – это операция проекции реляционной алгебры, поэтому каждое полученное при декомпозиции отношение называют проекциями первоначального.

Возникает вопрос: какие условия должны соблюдаться для того, чтобы проекции первоначального отношения при обратном соединении гарантировали получение исходного отношения? На этот вопрос дает ответ теорема Хеза:

Пусть R (А, В, С) – отношение, где А, В, С – подмножества множества его атрибутов.

Если R удовлетворяет ФЗ А → В, то R равно соединению его проекций {А, В} и {А, С}.

(Заметим, что теорема не утверждает «тогда и только тогда»).

3.2.3. Первая, вторая и третья нормальные формы

Отношение находится в 1 НФ тогда и только тогда, когда все используемые в нем домены содержат только скалярные значения.

Иными словами:

Отношение находится в 1 НФ тогда и только тогда, когда значения всех полей неделимы.

Например, если в отношении есть поле ФИО, отношение не находится в 1 НФ, т.к. значения этого поля можно разделить на фамилию, имя и отчество.

Отношение находится во 2 НФ тогда и только тогда, когда оно находится в 1 НФ и каждый неключевой атрибут неприводимо зависит от первичного ключа.

Например, рассмотрим отношение Успеваемость (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Дисциплина, Оценка).

Если первичным ключом здесь назначить №ЗачетнойКнижки, то от этого ключа не будет зависеть атрибут Дисциплина. Т.е. в этом случае отношение не находится во 2 НФ.

Можно тогда в качестве первичного ключа взять множество атрибутов {№ЗачетнойКнижки, Дисциплина}. В этом случае от такого ключа зависят все атрибуты, но атрибуты Фамилия, Имя, Отчество зависят приводимо, т.к. из детерминанта следующей ФЗ можно убрать атрибут Дисциплина без нарушения зависимости:

{№ЗачетнойКнижки, Дисциплина} → {Фамилия, Имя, Отчество}

И при таком первичном ключе отношение не находится во 2 НФ.

Чтобы получить отношения во 2 НФ произведем декомпозицию. Можно это сделать по теореме Хеза.

Отношение Успеваемость удовлетворяет ФЗ:

{№ЗачетнойКнижки} → {Фамилия, Имя, Отчество} (А → В)

Вне этой ФЗ осталось следующее множество атрибутов: {Дисциплина, Оценка} (С)

Тогда по теореме Хеза отношение Успеваемость равно соединению его проекций с такими множествами атрибутов:

{№ЗачетнойКнижки, Фамилия, Имя, Отчество} ({А, В})

{№ЗачетнойКнижки, Дисциплина, Оценка} ({А, С})

То есть, декомпозиция без потерь возможна на отношения:

Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество)

Успеваемость1 (№ЗачетнойКнижки, Дисциплина, Оценка).

Отношение находится в 3 НФ тогда и только тогда, когда оно находится во 2 НФ и каждый неключевой атрибут нетранзитивно зависит от первичного ключа.

Иными словами:

Отношение находится в 3 НФ тогда и только тогда, когда каждый кортеж отношения состоит из значения первичного ключа, которое идентифицирует некоторый объект, и набора взаимно независимых (или пустых) значений атрибутов, описывающих этот объект.

Например, добавим в отношение Студенты атрибут СтаростаГруппы. Тогда в отношении будут следующие ФЗ:

{№ЗачетнойКнижки} → {КодГруппы}, {КодГруппы} → {СтаростаГруппы}

То есть атрибут СтаростаГруппы зависит от первичного ключа (№ЗачетнойКнижки) транзитивно через атрибут КодГруппы, а не напрямую.

Значит, это отношение не находится в 3 НФ.

Проведем декомпозицию. В данном случае по теорема Хеза может быть два варианта декомпозиции.

1 вариант основан на ФЗ {№ЗачетнойКнижки}→{Фамилия, Имя, Отчество, КодГруппы}.

В результате получим такие проекции:

{№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы} и

{№ЗачетнойКнижки, СтаростаГруппы}

2 вариант основан на ФЗ {КодГруппы}→{СтаростаГруппы}.

В результате получим такие проекции:

{КодГруппы, СтаростаГруппы}

{КодГруппы, №ЗачентойКнижки, Фамилия, Имя, Отчество}

Подходит второй вариант, т.к. при первом варианте возможны ошибки при обновлении данных (пользователь может ввести для конкретного студента старосту неверно, и система не выдаст ошибки). Такая ситуация говорит о том, что теорема Хеза не всегда является удачным и единственным способом для выбора проекций при декомпозиции.

В результате при декомпозиции на две проекции

Группы (КодГруппы, СтаростаГруппы) и

Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы)

получим отношения в 3 НФ.

Таким образом, если отношение не находится ни во 2 НФ, ни в 3 НФ, существует избыточность, которая приводит к так называемым аномалиям обновления, т.е. нарушении целостности при вставке, удалении или изменении данных.

Например, рассмотрим отношение, которое не находится ни во 2 НФ, ни в 3 НФ.

Успеваемость (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, СтаростаГруппы, Дисциплина, Оценка).

Изобразим диаграмму ФЗ этого отношения:

Какие могут произойти аномалии при обновлении данных в таком отношении?

Например, такие:

При добавлении нового студента при правильном указании группы, в которой он учится, может быть ошибочно указан староста группы.
При удалении одной из записей будет удалена не только информация об оценке соответствующего студента, но и информация о том, в какой группе он учится.
При изменении старосты группы необходимо вручную изменить его для всех записей студентов этой группы – при этом можно ошибиться.

Для этого отношения можно произвести декомпозицию. Это удобно сделать, руководствуясь схемой. Например, на три следующие проекции:

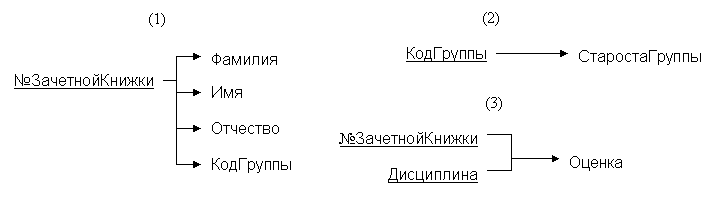
Все полученные отношения находятся во2 НФ и в 3 НФ.

Но без потерь ли произведена эта декомпозиция? Да, т.к. после соединения этих трех отношений получим первоначальное.

Полученные отношения являются независимыми проекциями.

Проекции R₁ и R₂ отношения R независимы тогда и только тогда, когда выполняются два условия:

1) каждая ФЗ в отношении R является логическим следствием ФЗ в проекциях R₁ и R₂;

2) общие атрибуты проекций R₁ и R₂ образуют потенциальный ключ хотя бы для одной из них.

Для наших трех проекций первое условие выполняется, т.к. все их ФЗ (обозначенные стрелками) обеспечивают ФЗ первоначального отношения.

Выполняется и второе условие: для проекций (1) и (2) общий атрибут – КодГруппы, он первичный ключ для (2); для (1) и (3) общий атрибут - №ЗачетнойКнижки, он первичный ключ для (1).

А вот если разбить отношение Успеваемость на следующие проекции:

(4)

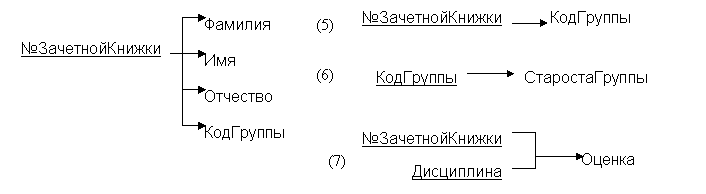
первое условие выполнится, а второе - не выполнится (атрибут КодГруппы общий для (4) и (5), но не является потенциальным ключом ни в одном из них). То есть, эти проекции не являются независимыми.

Отношение, которое не может быть подвергнуто декомпозиции с получением независимых проекций, называется атомарным.

Но это не означает, что любое неатомарное отношение может быть разбито на атомарные отношения. И не всегда есть смысл такого разбиения.

Например, отношение Студенты (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы) атомарно. А отношение Студенты1 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, КодГруппы, Адрес, ДомашнийТелефон) неатомарно, т.к. домашний телефон зависит от адреса, поэтому отношение Студенты1 можно разбить на такие независимые проекции: Студенты2 (№ЗачетнойКнижки, Фамилия, Имя, Отчество, Адрес) и АдресаТелефоны (Адрес, ДомашнийТелефон). Но в этом нет смысла.

3.2.4. Нормальная форма Бойса-Кодда

При определении 3 НФ делалось допущение о том, что отношение имеет только один потенциальный ключ, который и является первичным. Но определение 3 НФ не совсем подходит для отношений со следующими свойствами:

отношение имеет два или более потенциальных ключа;
потенциальные ключи сложные;
потенциальные ключи перекрываются, т.е имеют хотя бы один общий атрибут.

Для отношений, обладающих этими свойствами данного ранее определения 3 НФ недостаточно, поэтому Бойс и Кодд ввели определение НФ Бойса-Кодда.

Отношение находится в НФБК тогда и только тогда, когда каждая нетривиальная и неприводимая слева ФЗ обладает потенциальным ключом в качестве детерминанта.

На практике отношения с комбинацией перечисленных свойств встречаются крайне редко, а для отношений без этих свойств 3 НФ и НФБК эквивалентны.

Можно заметить, что определение НФБК проще, чем 3 НФ, т.к. в нем нет упоминания 2 НФ и не используется понятие транзитивной зависимости.

Например, рассмотрим отношение с двумя перекрывающимися потенциальными ключами.

Успеваемость (№ЗачетнойКнижки, КодДисциплины, НазваниеДисциплины, Оценка)

Потенциальные ключи: {№ЗачетнойКнижки, КодДисциплины} и {№ЗачетнойКнижки, НазваниеДисциплины}.

Это отношение не в НФБК, т.к. в нем есть такие ФЗ:

КодДисциплины → НазваниеДисциплины

НазваниеДисциплины → КодДисциплины

А детерминанты этих ФЗ не являются потенциальными ключами.

Это отношение также не в 3 НФ, т.к. не находится во 2 НФ, потому что атрибут НазваниеДисциплины зависит только от части первичного ключа (ФЗ {№ЗачетнойКнижки, КодДисциплины} → {НазваниеДисциплины} приводима).

Видно, что этому отношению присуща избыточность.

Возможна декомпозиция на два отношения:

Дисциплина (КодДисциплины, НазваниеДисциплины)

Успеваемость1 (№ЗачетнойКнижки, КодДисциплины, Оценка)

Рассмотрим пример отношения, которое находится в 3 НФ, но не находится в НФБК. Пусть в БД Факультет есть отношение Занятия (КодГруппы, Дисциплина, Преподаватель):

КодГруппы	Дисциплина	Преподаватель
ИНФ-21	ПО ЭВМ	Пятышева Е.А.
ИНФ-22	ПО ЭВМ	Суворова Т.Н.
ИНФ-31	СУБД	Шиляева М.С.
ИНФ-32	СУБД	Петухова М.В.
…

Введем следующие ограничения:

a) каждую дисциплину у конкретной группы ведет только один преподаватель, но одну и ту же дисциплину могут вести разные преподаватели;

b) каждый преподаватель ведет только одну дисциплину (в действительности это не всегда так, но мы предположим именно это).

Тогда существует два потенциальных ключа: {КодГруппы, Дисциплина} и {КодГруппы, Преподаватель}. Опять ситуация с двумя перекрывающимися потенциальными ключами. Первый из них назначим первичным.

Это отношение в 3 НФ, т.к.

Оно находится во 2 НФ. Докажем это: единственная ФЗ неключевого атрибута {КодГруппы, Дисциплина} → Преподаватель. Она неприводима, т.к. атрибут КодГруппы из детерминанты исключить нельзя (одну и ту же дисциплину могут вести разные преподаватели, т.е. не верна ФЗ Дисциплина → Преподаватель); атрибут Дисциплина тоже исключить нельзя (группа изучает несколько дисциплин у разных преподавателей, т.е. не верна ФЗ КодГруппы → Преподаватель).
Отношение находится и в 3 НФ. Докажем это: в единственной ФЗ для неключекого атрибута (см. 1) этот неключевой атрибут нетранзитивно зависит от первичного ключа.

Но это отношение не в НФБК, т.к. есть ФЗ Преподаватели → Дисциплины (по условию каждый преподаватель может вести только одну дисциплину), и детерминант этой ФЗ не является потенциальным ключом.

Поэтому в отношении Занятия могут произойти аномалии обновления. Например, если требуется удалить информацию о группе ИНФ-31, то при этом утратится информация о том, что дисциплину СУБД ведет преподаватель Шиляева М.С.

Необходима декомпозиция на проекции, которые будут в НФБК:

ГП (Группа, Преподаватель) и ПД (Преподаватель, Дисциплина)

Но эти проекции не являются независимыми, т.к. при попытке вставить новую запись в одну из них может возникнуть противоречие. Например, вставляем в отношение ГП кортеж {ИНФ-31, Васенина Е.А.}, но если, допустим, Васенина Е.А. преподает дисциплину ИТО, и в этом отношении есть уже кортеж {ИНФ-31, Огородников Е.В.} и преподаватель Огородников Е.В. тоже преподает дисциплину ИТО. Возникнет противоречие (два преподавателя ведут одну дисциплину у одной группы). А проверить это можно только в отношении ПД.

Вывод: не всегда можно достичь две цели сразу – разбить на отношения в НФБК и чтобы эти отношения были независимы.

Действительно, отношение Занятия является атомарным, но атомарность не является ни необходимым, ни достаточным условие хорошего макета БД. А если стремиться к НФБК, то это в некоторых случаях усложняет БД.

Все это показывает, что на практике целей лучше избегать отношений с перекрывающимися потенциальными ключами, тогда достаточно 3 НФ.

Но если без них сложно обойтись, то вводят особые правила обновления, в каждом конкретном случае – свои.

3.3. Нормальные формы более высокого порядка

3.3.1. Многозначные зависимости

Для введения 4 НФ необходимо ввести понятие многозначной зависимости (МЗ).

Пусть А, В, С – произвольные подмножества множества атрибутов отношения R.

Тогда В многозначно зависит от А тогда и только тогда, когда множество значений В, соответствующее заданной паре значений (значение А, значение С) отношения R, зависит только от А, но не зависит от С.

Обозначается: А 8 В

Говорится: «А многозначно определяет В» или «В многозначно зависит от А» или «А двойная стрелка В».

Упрощенно можно сказать так: А многозначно определяет В, если для каждого значения А не существует единственного соответствующего ей значения В (не верна ФЗ А ® В), но каждое значение А определяет множество соответствующих ей значений В.

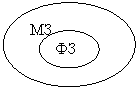По сути ФЗ – это частный случай МЗ:

Пример, который пояснит суть МЗ:

Пусть имеется отношение ДПК (Дисциплина, Преподаватель, Кабинет).

Дисциплина	Преподаватель	Кабинет
ИС	Огородников Е.В.	140
ИС	Огородников Е.В.	218
ИС	Шиляева М.С.	140
ИС	Шиляева М.С.	218
СУБД	Шиляева М.С.	315
СУБД	Шиляева М.С.	411
СУБД	Петухова М.В.	315
СУБД	Петухова М.В.	411
…

Введем следующие ограничения:

a) каждой дисциплине может соответствовать любое количество преподавателей и любое количество кабинетов;

b) преподаватели и кабинеты не зависят друг от друга (т.е. независимо от того, кто преподает данную дисциплину, для этой дисциплины используется один и тот же набор кабинетов);

c) конкретный преподаватель и конкретный кабинет могут быть связаны с любым количеством дисциплин.

В этом случае первичный ключ – множество всех атрибутов.

Проверим, в каких НФ находится это отношение.

1) 1 НФ – т.к. атрибуты неделимы (будем считать, что вместо ФИО преподавателя используется некий код преподавателя, но для удобства в примере будем использовать ФИО).

2) 2 НФ – т.к. неключевых атрибутов вообще нет.

3) 3 НФ – по той же причине.

4) НФБК – не подходит для этого отношения, т.к. в нем нет нескольких перекрывающихся потенциальных ключей.

Попутно можно сделать вывод, что полностью ключевое отношение (если оно в 1 НФ) находится в 3 НФ и в НФБК.

По ограничению b) можно утверждать, что если существуют два кортежа

{Дисциплина1, Преподаватель1, Кабинет1} и

{Дисциплина1, Преподаватель2, Кабинет2},

то существуют и кортежи

{Дисциплина1, Преподаватель1, Кабинет2} и

{Дисциплина1, Преподаватель2, Кабинет1}.

Например, если существуют кортежи

{СУБД, Шиляева М.С., 315} и

{СУБД, Петухова М.В., 411},

то существуют и кортежи

{СУБД, Шиляева М.С., 411} и

{СУБД, Петухова М.В., 315}.

В этом случае отношение явно избыточно и может привести к аномалиям обновления. Например, для добавления информации о том, что дисциплина СУБД будет вестись новым преподавателем Ивановым И.И. необходимо создать столько новых кортежей, сколько кабинетов подходят для этой дисциплины. А при этом ошибочно можно ввести кортежи не для всех кабинетов или, наоборот, с лишними кабинетами.

Существование подобных проблем вызвано, как правило, независимостью атрибутов. В нашем примере – атрибутов Преподаватель и Кабинет.

Как исправить ситуацию, чтобы избежать избыточности и аномалий обновления?

Можно заменить отношение ДПК двумя его проекциями:

ДП (Дисциплина, Преподаватель) и ДК (Дисциплина, Кабинет)

Обе проекции полностью ключевые, следовательно, находятся в НФБК.

Кроме того, это декомпозиция без потерь, т.к. при соединении обратно по атрибуту Дисциплина получим первоначальное отношение ДПК.

Можно сказать, что все эти рассуждения были на интуитивном уровне, из соображений здравого смысла – мы не пользовались какими-либо строгими правилами.

Только в 1971 году эти соображения были формализованы Фейгином с помощью понятия многозначных зависимостей.

Формализуем процесс декомпозиции отношения ДПК. Этого нельзя сделать, основываясь на ФЗ, т.к. диаграмма ФЗ выглядит так:

И все ФЗ здесь тривиальны.

Но произведенную декомпозицию можно сделать на основе МЗ, т.к. в отношении их две:

Дисциплина 8 Преподаватель

Дисциплина 8 Кабинет

Первая означает, что хотя для каждой дисциплины не существует единственного соответствующего ей преподавателя (не верна ФЗ Дисциплина ® Преподаватель), но каждая дисциплина определяет множество соответствующих ей преподавателей.

Вторая означает, что хотя для каждой дисциплины не существует единственного соответствующего ей кабинета (не верна ФЗ Дисциплина ® Кабинет), но каждая дисциплина определяет множество соответствующих ей кабинетов.

По этим МЗ и можно произвести декомпозицию.

Можно заметить, что для отношения ДПК многозначная зависимость Дисциплина 8 Преподаватель выполняется тогда и только тогда, когда выполняется МЗ Дисциплина 8 Кабинет.

Для подобных отношений это выполняется всегда, т.е. в обобщенном виде можно сформулировать правило многозначных зависимостей:

Для R (А, В, С) А 8 В тогда и только тогда, когда А 8 С.

Таким образом, МЗ образуют пары и их обычно представляют так: А 8В½С.

Для ДПК можно записать Дисциплины 8 Преподаватели½Кабинеты.

Теорема Фейгина:

Пусть А, В, С – подмножества множества атрибутов отношения R. Отношение R будет равно соединению его проекций {А, В} и {А, С} тогда и только тогда, когда для отношения R выполняется МЗ А 8В½С.

3.3.2. Четвертая нормальная форма

Отношение R находится в 4 НФ тогда и только тогда, когда

если существуют такие подмножества А и В множества атрибутов R, что выполняется нетривиальная МЗ А 8 В,

то все атрибуты отношения R функционально зависят от атрибута А.

Другая формулировка:

Отношение R находится в 4 НФ если оно находится в НФБК и все МЗ отношения R фактически являются ФЗ от потенциальных ключей.

Отношение ДПК из предыдущего примера не находится в 4 НФ, т.к. (по первой формулировке):

1) Существует МЗ Дисциплина 8 Преподаватель, но при этом атрибут Кабинет не зависит функционально от атрибута Дисциплина.

2) Существует МЗ Дисциплина 8 Кабинет, но при этом атрибут Преподаватель не зависит функционально от атрибута Дисциплина.

Но обе проекции ДП и ДК находятся в 4 НФ, т.к. в каждой из них существует по одной МЗ, и других атрибутов (не входящих в эти МЗ) нет.

Фейгин доказал также, что 4 НФ всегда может быть получена, т.е. любое отношение, содержащее МЗ может быть подвергнуто декомпозиции без потерь на набор отношений в 4 НФ.

3.3.3. Зависимость соединения

Не всегда можно произвести декомпозицию без потерь одного отношения на две проекции. Если это невозможно, но возможно разбить отношение на три или более проекций, такое отношение называют n-декомпозируемым, где n – число проекций, на которое можно разбить отношение без потерь.

Например, рассмотрим отношение ЛДС (Литература, Дисциплина, Специальность), полностью ключевое. Это отношение выражает информацию о том, что некая имеющаяся в библиотеке книга подходит для некоторой дисциплины, изучаемой определенной специальностью.

Отношение ЛДС:

Литература	Дисциплина	Специальность
Хомоненко А. и др. Базы данных	СУБД	Информатика с доп. спец. ин. язык
Хомоненко А. и др. Базы данных	ИС	Математика с доп. спец. информатика
Хомоненко А. и др. Базы данных	ИС	Информатика с доп. спец. ин. язык
Дейт К. Введение в системы баз данных	СУБД	Информатика с доп. спец. ин. язык
Дейт К. Введение в системы баз данных	ИС	Информатика с доп. спец. ин. язык

Произведем декомпозицию на три проекции: ЛД, ДС, ЛС.

ЛД ДС ЛС

Литература	Дисциплина	Дисциплина	Специальность	Литература	Специальность
Хомоненко	СУБД	СУБД	Информатика	Хомоненко	Информатика
Хомоненко	ИС	ИС	Математика	Хомоненко	Математика
Дейт	СУБД	ИС	Информатика	Дейт	Информатика
Дейт	ИС

Соединим обратно только две проекции, ЛД и ДС по атрибуту Дисциплина, и сравним кортежи полученного отношения с кортежами первоначального отношения ЛДС:

Литература	Дисциплина	Специальность
Хомоненко	СУБД	Информатика	- есть
Хомоненко	ИС	Математика	- есть
Хомоненко	ИС	Информатика	- есть
Дейт	СУБД	Информатика	- есть
Дейт	ИС	Математика	- нет!
Дейт	ИС	Информатика	- есть

В результате получили лишний кортеж.

Аналогичная ситуация будет и при соединении ЛД и ЛС, а также ДС и ЛС.

А если соединить все три проекции, то получим именно первоначальное отношение ЛДС.

Таким образом, можно сделать вывод, что отношение ЛДС 3-декомпозируемо.

В связи с такими n-декомпозициями вводится понятие зависимости соединения (ЗС), на основе которого затем определяется 5 НФ.

Пусть R – отношение, А, В, …, Z – произвольные подмножества множества атрибутов R.

Отношение R удовлетворяет зависимости соединения *(А, В, …, Z) тогда и только тогда, когда оно равносильно соединению своих проекций с подмножествами атрибутов А, В, …, Z.

Для нашего примера отношение ЛДС удовлетворяет зависимости соединения

*(ЛД, ДС, ЛС) или

*({Литература,Дисциплина},{Дисциплина,Специальность},{Литература,Специальность}).

Как ФЗ является частным случаем МЗ, так и МЗ является частным случаем ЗС.

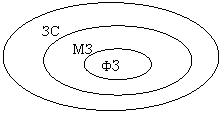3.3.4. Пятая нормальная форма

Отношение R находится в 5 НФ, которая также называется проекционно-соединительной НФ, тогда и только тогда, когда каждая ЗС в отношении R подразумевается потенциальными ключами отношения R.

Например, рассмотрим отношение Группы (КодГруппы, НазваниеГруппы, Курс, Староста). Имеется два потенциальных ключа: КодГруппы и НазваниеГруппы. Эти ключи подразумевают (т.е. обеспечивают) такие, например, ЗС:

*({КодГруппы, Староста}, {КодГруппы, НазваниеГруппы, Курс})

*({КодГруппы, НазваниеГруппы}, {КодГруппы, Курс}, {НазваниеГруппы, Староста})

и т.п.

А если убрать альтернативный ключ (НазваниеГруппы), оставив единственный потенциальный ключ (КодГруппы), то еще проще:

*({КодГруппы, Курс}{КодГруппы, Староста})

и всё.

Рассмотренное в предыдущем примере отношение ЛДС не в 5 НФ, т.к. ЗС *(ЛД, ДС, ЛС) не подразумевается единственным в этом отношении потенциальным ключом {Литература, Дисциплина, Специальность}.

Найти все ЗС гораздо сложнее, чем ФЗ и МЗ, - нет точного алгоритма такого поиска. То есть процесс проверки отношения на 5 НФ не определен достаточно четко. Утешает то, что на практике подобные отношения встречаются редко.

Из определения 5 НФ можно сделать вывод, что эта НФ является окончательной по отношению к проекции и соединению (это и отражено в ее втором названии).

Таким образом, гарантируется, что отношение в 5 НФ не содержит избыточности данных, которые могут привести к аномалиям обновления.

3.4. Итоговая схема процедуры нормализации

В общем случае можно выделить следующие четыре цели процедуры нормализации:

Исключение избыточности.
Устранение аномалий обновления.
Проектирование макета данных, который соответствовал бы реальному миру, был интуитивно понятен и служил основой для дальнейшего развития.
Упрощение процесса наложения ограничений целостности. Эта цель связана с потенциальными ключами, т.е. если соблюдать условие уникальности потенциальных ключей и организовывать связи только через них, то эта цель будет достигнута.

Пусть имеется отношение R, которое находится в 1 НФ. Также известны все ограничения этого отношения, т.е. ключи, ФЗ, МЗ и ЗС.

Тогда основная идея нормализации отношения R состоит в декомпозиции без потерь, принципы которой в следующем:

·последовательно отношение R приводится к набору меньших отношений, который эквивалентен отношению R, но более предпочтителен;

·каждый этап этого процесса состоит из разбиения на проекции отношений, полученных на предыдущем этапе;

·при этом все заданные зависимости (ФЗ, МЗ, ЗС) используются на каждом шаге для выбора проекций следующего этапа.

Перечислим основные правила, на которые опирается процедура нормализации.

Отношение в 1 НФ следует разбить на проекции для исключения всех приводимых ФЗ. В результате – набор отношений во 2 НФ.
Отношения во 2 НФ следует разбить на проекции для исключения всех транзитивных ФЗ. В результате – набор отношений в 3 НФ.
Отношение в 3 НФ следует разбить на проекции для исключения всех оставшихся ФЗ, в которых детерминанты не являются потенциальными ключами. В результате – набор отношений в НФБК.
(Заметим, что все первые три правила можно сконцентрировать в одном: «исходное отношение следует разбить на проекции для исключения всех ФЗ, в которых детерминанты не являются потенциальными ключами»)
Отношение в НФБК следует разбить на проекции для исключения всех МЗ, которые не являются ФЗ. В результате – набор отношений в 4 НФ. (На практике такие МЗ обычно исключаются перед первым этапом, т.е. отделяются независимые повторяющиеся группы)
Отношение в 4 НФ следует разбить на проекции для исключения всех ЗС, которые не подразумеваются потенциальными ключами (если такие ЗС можно выявить). В результате – набор отношений в 5 НФ.

К правилам можно выделить следующие дополнения:

Процесс разбиения на проекции должен быть выполнен без потерь и с сохранением зависимостей исходных данных.
При проверке на НФБК, 4 НФ и 5 НФ можно пользоваться их альтернативными определениями, что иногда бывает удобнее, - в зависимость от конкретной ситуации.
Бывают ситуации, когда удобнее менять последовательность процедуры нормализации.
Хотя идеи нормализации важны и наиболее приемлемы для проектирования БД, они не являются универсальным средством по следующим причинам:
- кроме ФЗ, МЗ и ЗС существуют и другие типы зависимостей и ограничений – специфические для каждой БД;
- декомпозиция может быть не уникальной, т.е. могут существовать разные ее варианты. А для выбора предпочтительного не так уж много критериев;
- не всякую избыточность данных можно устранить разбиением на проекции.

Но, несмотря на эти замечания, можно сказать, что методика нисходящего проектирования БД, реализованная в нормализации отношений, позволяет создать непротиворечивый, нормализованный макет БД.