Б.2.1. Элементы задачи теории принятия решений
Б.2.2. Проверка методом отношения правдоподобий и критерий максимума апостериорной вероятности
Б.3. Пример обнаружения сигнала
Б.3.1. Двоичное решение по принципу максимального правдоподобия
Б.1. Теорема Байеса
Математические основы проверки гипотез базируются на теореме Байеса, которая следует из определения отношения между условной вероятностью и совместной вероятностью случайных переменных A и В.
Р(А|В)Р(В) = Р(В|А)Р(А) = Р(А,В) (Б.1)
Теорема формулируется следующим образом.
Р(А|В)=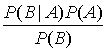
(Б.2)
Теорема Байеса позволяет выводить условную вероятность Р(А|В) из условной вероятности Р(В|А).
Б. 1.1. Дискретная форма теоремы Байеса
Теорему Байеса можно записать в дискретной форме следующим образом.
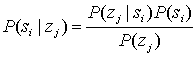i = 1, …, M; j = 1, … (Б.З) где
В приложениях связи si - это i-й класс сигнала из набора М классов, a zj - j-я выборка принятого сигнала. Уравнение (Б.З) можно рассматривать как описание эксперимента, в котором задействована принятая выборка и некоторые статистические знания о классах сигнала, к которым может принадлежать эта принятая выборка. До эксперимента вероятность появления i-гo класса сигнала P(si) называется априорной. В результате изучения конкретной принятой выборки zj из плотности условной вероятности P(zj|si) можно найти статистическую меру правдоподобия принадлежности zj к классу si. После эксперимента можно вычислить апостериорную вероятность P(si|zj), которую можно рассматривать как "уточнение" наших априорных знаний. Таким образом, к эксперименту мы приступаем, имея некоторые априорные знания, касающиеся вероятности состояния природы, а после изучения выборочного сигнала получаем апостериорную ("после свершения") вероятность. Параметр P(zj) — это вероятность принятой выборкиzj, во всем пространстве классов сигналов. Этот термин, P(zj), можно рассматривать как масштабный множитель, поскольку его значение одинаково для всех классов сигнала.
Пример Б.1. Использование (дискретной формы) теоремы Байеса
Имеется два ящика деталей. Ящик 1 содержит 1000 деталей, 10% из которых неисправны, а ящик 2 — 2000 деталей, из которых неисправными являются 5%. Если в результате случайного выбора ящика и детали из него деталь оказывается исправной, то чему равна вероятность того, что данная деталь взята из ящика 1?
Решение
P (ящик 1|ИД) = Р(ИД | ящик 1)/Р(ИД),
где ИД означает "исправная деталь".
Р(ИД) = Р(ИД | ящик 1)Р(ящик 1) + Р(ИД | ящик 2)Р(ящик 2) =
= (0,90)(0,5) + (0,95)(0,5) = 0,450 + 0,475 = 0,925
Р(ящик 1| ИД) =
= 0,486
До эксперимента априорные вероятности выбора ящика 1 или 2 равны. После получения исправной детали вычисления, проведенные согласно теореме Байеса, могут рассматриваться как способ "точной подстройки" нашего представления о том, что Р(ящик 1) = 0,5, в результате которой возникает апостериорная вероятность 0,486. Теорема Байеса — это просто формализация здравого смысла. Если была получена исправная деталь, то не кажется ли вам (интуитивно), что она с большей вероятностью могла быть взята из ящика с более высокой концентрацией исправных деталей и с меньшей - из ящика с меньшей концентрацией? Теорема Байеса уточняет априорную статистику выбора ящиков, порождая апостериорную статистику.
Пример Б.2. Применение теории принятия решений в теории игр
В ящике находится три монеты: обычная, с двумя орлами и с двумя решками. Вам предлагается случайным образом вытянуть одну монету, взглянуть на одну ее сторону и угадать, что находится на другой стороне. Какой стратегии лучше всего придерживаться?
Решение
Данную задачу можно рассматриваться как задачу обнаружения сигнала. Сигнал передается, но вследствие шума канала принятый сигнал не совсем отчетлив. Невозможность взглянуть на обратную сторону монеты равносильна приему сигнала, возмущенного шумом. Пусть Hi представляет гипотезу (i = П, О, Р), где индексы П, О и Р обозначают правильную монету, монету с двумя орлами и монету с двумя решками.
НП = О,Р (правильная монета)
НО = О,О (монета с двумя орлами)
НР= Р, Р (монета с двумя решками)
Пусть zj представляет принятую выборку (j=O,P), где zO - орел, аzO - решка. Пусть априорные вероятности гипотез равновероятны, так что Р(НП) = =Р(НО) = Р(НР) = 1/3. Используем теорему Байеса.
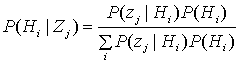
Нам необходимо вычислить вероятности всех гипотез для всех классов сигнала. Следовательно, нам нужно изучить результаты шести вычислений, после чего мы сможем установить оптимальную стратегию принятия решения. В каждом случае значение 
можно вычислить из условных вероятностей, изображенных на рис. Б.1. Пусть мы выбрали монету и увидели орел (zO), тогда вычисление трех апостериорных вероятностей дает следующие результаты.
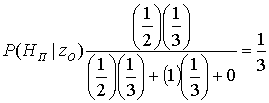
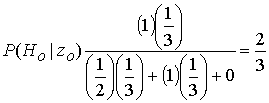
P(HP / zO) = 0
Если принятой выборкой является решка (zP), вычисления дают следующее.
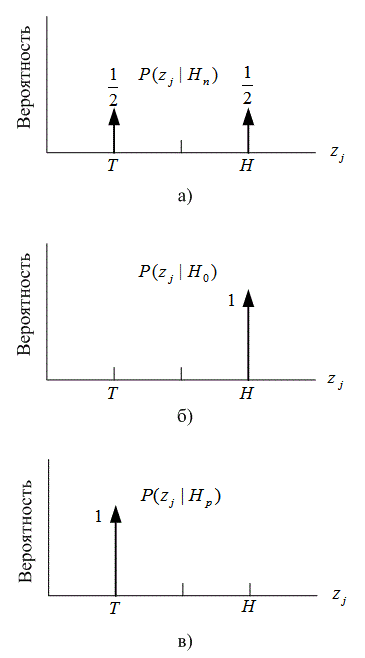
Рис. Б.1. Условная вероятность :
а) для правильной монеты; б) для монеты с двумя орлами;
в) для монеты с двумя решками
Таким образом, оптимальной стратегией принятия решения является следующая: если принят орел (zO), выбрать гипотезу НO (соответствующую монете с двумя орлами); если принята решка (zP), выбрать гипотезу HP (соответствующую монете с двумя решками).
Б.1.2. Теорема Байеса в смешанной форме
Для большинства приложений связи, представляющих практический интерес, возможные значения принятой выборки принадлежат непрерывному диапазону (причина - наличие в канале связи аддитивного гауссового шума). Следовательно, наиболее полезная форма теоремы Байеса содержит плотность вероятности с непрерывными, а не дискретными значениями. Изменим соответствующим образом формулу (Б.З).
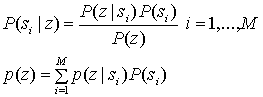(Б.4)
Здесь 
- плотность условной вероятности принятой выборки z (принимающей значения из непрерывного диапазона) при условии принадлежности к классу si.
Пример Б.З. Наглядное представление теоремы Байеса
Даны два класса сигнала s1 и s2, которые описываются треугольными функциями плотности условной вероятности 
и 
, показанными на рис. Б.2. Принят некоторый сигнал; он может иметь любое значение по оси z. Если функции плотности вероятности не перекрываются, сигнал можно классифицировать однозначно. В данном же примере, приведенном на рис. Б.2, нам требуется правило, которое позволит классифицировать принятые сигналы, поскольку некоторые из них попадут в область перекрывающихся функций плотности вероятности. Рассмотрим принятый сигнал za. Пусть два класса сигналов s1 и s2 являются равновероятными. Нужно вычислить две возможные апостериорные вероятности и предложить правило принятия решений, которое следует использовать при определении принадлежности сигнала za к определенному классу. То же самое нужно сделать для сигнала zb.
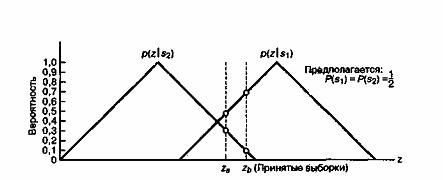
Рис. Б.2. Наглядное представление теоремы Байеса
Решение
Из рис. Б.2 видим, что 
= 0,5 и 
= 0,3. Следовательно,
=
=
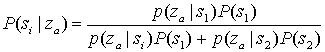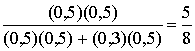
и
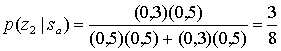
Одно из возможных правил - определять принятый сигнал к классу с максимальной апостериорной вероятностью (классу S1). Эквивалентное правило, для равных априорных вероятностей, - это исследовать значение функции плотности вероятности, обусловленной каждым классом сигналов (называемой правдоподобием класса сигналов), и выбрать класс с максимальным значением. Рассмотрим рис. Б.2 и отметим, что правило максимального правдоподобия соответствует нашей интуиции. Правдоподобие принадлежности сигналаza к каждому классу сигналов соответствует обведенной кружком точке на каждой функции плотности вероятности. Правило максимального правдоподобия заключается в выборе класса сигналов, дающего максимальную условную вероятность из всех имеющихся. Повторим вычисления для принятого сигнала zb.
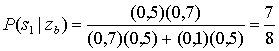
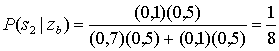
Как и ранее, правило максимального правдоподобия указывает нам выбрать класс сигналов s1. Заметим, что при принятии выборки zb, мы более уверены в точности нашего выбора, по сравнению с принятием, сигнала za. Это объясняется тем, что отношение 
к существенно больше отношения к 
.
Б.2. Теория принятия решений
Б.2.1. Элементы задачи теории принятия решений
После того как мы описали проверку гипотез на основе статистики Байеса, перейдем к рассмотрению элементов задачи теории принятия решений в контексте системы связи, как показано на рис. Б.З. Источник сигнала в передатчике состоит из множества {si(t)}, i = 1, ..., М сигналов (или гипотез). Принимается сигнал r(t) = si(t) + n(t), где n(t) — присутствующий в канале аддитивный белый гауссов шум (additive white Gaussian noise — AWGN). В приемнике сигнал сокращается до единственного числа z (t = T), которое может принимать любое значение. Поскольку шум является гауссовым процессом и приемник предполагается линейным, выход z(t) также есть гауссовым процессом [1], а число z(T) — случайной переменной, принимающей значения из непрерывного диапазона.
z(T) = ai(T) + n0(T) (Б.5)
Выборка z(T) составляется из сигнального компонента аi(Т) и шумового компонента п0(Т). Время Т - это длительность символа. В каждый момент времени kT, где k - целое, приемник использует правило принятия решения для определения принадлежности принятого сигнала к определенному классу сигнала. Для простоты записи выражение (Б.5) иногда используют в виде z = ai + n0, где функциональная зависимость от T не выражается явно.
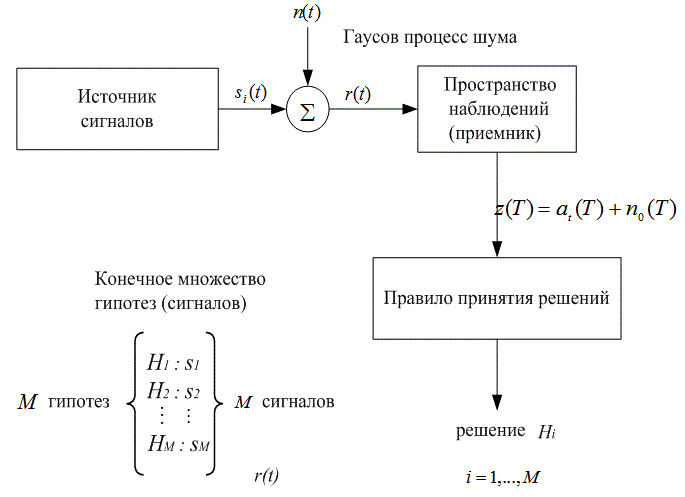
Рис. Б.3. Элементы задачи теории принятия решений в контексте системы связи
Б.2.2. Проверка методом отношения правдоподобий и критерий максимума апостериорной вероятности
При определении правила принятия решения для двух классов сигналов разумно начать со следующего соотношения.
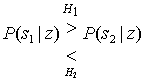(Б.6)
Выражение (Б.6) — это сокращенная запись следующего утверждения: "выбрать гипотезу H1 если апостериорная вероятность P(s1|z) больше апостериорной вероятности P(s2|z); в противном случае выбрать гипотезу H2".
Апостериорные вероятности в формуле (Б.6) можно заменить эквивалентными выражениями, полученными вследствие использования теоремы Байеса (уравнение (Б.4)), что дает следующее.
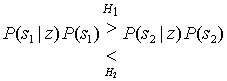(Б.7)
Итак, у нас есть правило принятия решения, выраженное через плотности вероятности (правдоподобия). Если переписать выражение (Б.7) и привести его к следующему виду
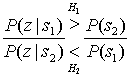(Б.8)
то отношение в левой части будет называться отношением правдоподобий, а все выражение часто именуют критерием отношения правдоподобий. Выражение (Б.8) — это принятие решений на основе сравнения принятого сигнала с порогом. Поскольку проверка опирается на выбор класса сигналов с максимальной апостериорной вероятностью, критерий принятия решения часто называется критерием максимума апостериорной вероятности (maximum a posteriori — MAP). Другое название — критерий минимума ошибки, поскольку в среднем он дает минимальное количество неверных решений. Стоит отметить, что данный критерий является оптимальным, только если ошибки всех типов наносят одинаковый вред (или имеют равную цену). Если ошибки некоторых типов обходятся дороже других, необходимо применять критерий, который учитывал бы относительные стоимости ошибок [1].
Б.2.3. Критерий максимального правдоподобия
Довольно часто сведения об априорных вероятностях гипотез или классов сигналов отсутствуют. Даже при наличии такой информации ее точность иногда вызывает сомнения. В таких случаях решения обычно принимаются исходя из предположения о возможности наиболее выгодной априорной вероятности; иными словами, значения априорных вероятностей выбираются так, чтобы классы были равновероятными. Если выбран такой подход, то критерий принятия решения является критерием максимального правдоподобия, и выражение (Б.8) записывается в следующем виде.
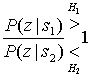(Б.9)
Отметим, что критерий максимального правдоподобия, приведенный в выражении (Б.9), аналогичен правилу максимального правдоподобия, описанному в примере Б.З.
Б.3. Пример обнаружения сигнала
Б.3.1. Двоичное решение по принципу максимального правдоподобия
В наглядном представлении процесса принятия решения (пример Б.З) фигурировали треугольные функции плотности вероятности. На рис. Б.4 приведены функции плотностей условных вероятностей для двоичных выходных сигналов, искаженных шумом: z(T) = а1+ п0 и z(T) = а2 + n0. Сигналы а1и а2взаимно независимы и равновероятны. Шум n0 предполагается независимой гауссовой случайной переменной с нулевым средним, дисперсией 
и плотностью вероятности, описываемой следующей формулой.
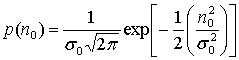(Б.10)
Следовательно, отношение правдоподобий, выраженное в формуле (Б.8), можно записать следующим образом.
= 
=
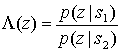
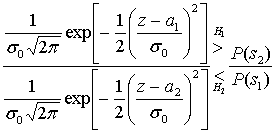
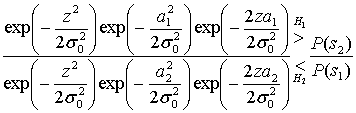(Б.11)
=
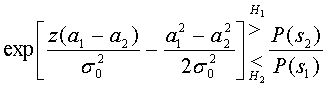
Здесь a1 — сигнальный компонент на выходе приемника при переданном s1(t), а а2— сигнальный компонент на выходе приемника при переданном s2(t). Неравенство (Б. 11) сохраняется при любом монотонно возрастающем (или убывающем) преобразовании.
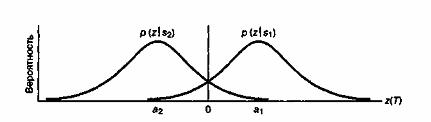
Рис. Б.4. Плотности условных вероятностей для типичного двоичного приемника
Следовательно, для упрощения выражения (БЛ1) от его обеих частей можно взять натуральный логарифм, что даст логарифмическое отношение правдоподобий.
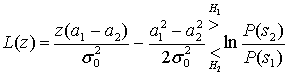(Б.12)
Если классы равновероятны, то
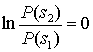
так что
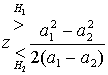(Б.13)
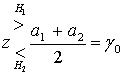
Для антиподных сигналов s1(t) = - s2(t) и a1 = -а2, так что можем записать следующее.
(Б.14)
Следовательно, правило максимального правдоподобия для равновероятных антиподных сигналов заключается в сравнении принятой выборки с нулевым порогом, что равносильно выбору s1(t), если выборка положительна, и выбору s2(t) — если она отрицательна.
Б.3.2. Вероятность битовой ошибки
Для двоичного примера, приведенного в разделе Б.3.1, рассчитаем вероятность битовой ошибки РВс помощью правила принятия решений из формулы (Б.13). Вероятность ошибки вычисляется путем суммирования вероятностей различных возможностей появления ошибки.
PB = P(H2|sl)P(sl) + P(H1|s2)P(s2) (Б.15)
Другими словами, при переданном сигнале s1(t) ошибка произойдет, если будет выбрана гипотеза H2; или ошибка произойдет, если при переданном сигнале s2(t) будет выбрана гипотеза H1. Для частного случая симметричных функций плотности вероятности и для P(s1) = P(s2) = 0,5 можем записать следующее.
PB = P(H2|sl) = P(H1|s2) (Б.16)
Вероятность ошибки РВравна вероятности принятия неверной гипотезы Н1при переданном сигнале s2(t) или принятия неверной гипотезы Н2при переданном сигнале s1(t). Следовательно, РB численно равна площади под хвостом любой функции плотности вероятности, 
или 
, "заползающим" на неверную сторону порога. Таким образом, РВмы можем вычислить, проинтегрировав от 
до 
или от до 
.
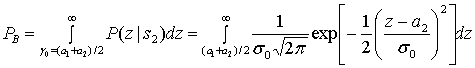(Б.17)
Пусть
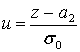
Тогда 
и
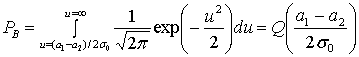, (Б.18)
где Q(x), именуемая гауссовым интегралом ошибок [1], протабулирована в табл. Б.1.
Таблица Б.1. Гауссов интеграл ошибок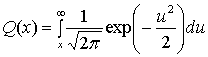 
|
Q(x) |
||||||||||
|
x |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 |
0,5000 0,4602 0,4207 0,3821 0,3446 0,3085 0,2743 0,2420 0,2169 0,1841 0,1587 0,1357 0,1151 0,0968 0,0808 0,0668 0,0548 0,0446 0,0359 0,0287 0,0228 0,0179 0,0139 0,0107 0,0082 0,0062 0,0047 0,0035 0,0026 0,0019 0,0013 0,0010 0,0007 0,0005 0,0003 |
0,4960 0,4562 0,4168 0,3783 0,3409 0,3050 0,2709 0,2389 0,2090 0,1814 0,1562 0,1355 0,1131 0,0951 0,0793 0,0655 0,0537 0,0436 0,0351 0,0281 0,0222 0,0174 0,0136 0,0104 0,0080 0,0060 0,0045 0,0034 0,0025 0,0018 0,0013 0,0009 0,0007 0,0005 0,0003 |
0,4920 0,4522 0,4129 0,3745 0,3372 0,3015 0,2676 0,2358 0,2061 0,1788 0,1539 0,1314 0,1112 0,0934 0,0778 0,0643 0,0526 0,0427 0,0344 0,0274 0,0217 0,0170 0,0132 0,0102 0,0078 0,0059 0,0044 0,0033 0,0024 0,0018 0,0013 0,0009 0,0006 0,0005 0,0003 |
0,4880 0,4483 0,4090 0,3707 0,3336 0,2981 0,2643 0,2327 0,2033 0,1762 0,1515 0,1292 0,1093 0,0918 0,0764 0,0630 0,0516 0,0418 0,0336 0,0268 0,0212 0,0166 0,0129 0,0099 0,0075 0,0057 0,0043 0,0032 0,0023 0,0017 0,0012 0,0008 0,0006 0,0004 0,0003 |
0,4840 0,4443 0,4052 0,3669 0,3300 0,2946 0,2611 0,2296 0,2005 0,1736 0,1492 0,1271 0,1075 0,0901 0,0749 0,0618 0,0505 0,0409 0,0329 0,0262 0,0207 0,0162 0,0125 0,0096 0,0073 0,0055 0,0041 0,0031 0,0023 0,0016 0,0012 0,0008 0,0006 0,0004 0,0003 |
0,4801 0,4404 0,4013 0,3632 0,3264 0,2912 0,2578 0,2266 0,1997 0,1711 0,1469 0,1251 0,1056 0,0885 0,0735 0,0606 0,0495 0,0401 0,0322 0,0256 0,0202 0,0158 0,0122 0,0094 0,0071 0,0054 0,0040 0,0030 0,0022 0,0016 0,0011 0,0008 0,0006 0,0004 0,0003 |
0,4761 0,4364 0,3974 0,3594 0,3228 0,2877 0,2546 0,2236 0,1949 0,1685 0,1446 0,1230 0,1038 0,0869 0,0721 0,0594 0,0485 0,0392 0,0314 0,0250 0,0197 0,0154 0,0119 0,0091 0,0069 0,0052 0,0039 0,0029 0,0021 0,0015 0,0011 0,0008 0,0006 0,0004 0,0003 |
0,4721 0,4625 0,3936 0,3557 0,3192 0,2843 0,2514 0,2206 0,1922 0,1660 0,1423 0,1210 0,1020 0,0853 0,0708 0,0582 0,0475 0,0384 0,0307 0,0244 0,0192 0,0150 0,0116 0,0089 0,0068 0,0051 0,0038 0,0028 0,0021 0,0015 0,0011 0,0008 0,0005 0,0004 0,0003 |
0,4681 0,4286 0,3897 0,3520 0,3156 0,2810 0,2483 0,2168 0,1894 0,1635 0,1401 0,1190 0,1003 0,0838 0,0694 0,0571 0,0465 0,0375 0,0301 0,0239 0,0188 0,0146 0,0113 0,0087 0,0066 0,0049 0,0037 0,0027 0,0020 0,0014 0,0010 0,0007 0,0005 0,0004 0,0003 |
0,4641 0,4247 0,3859 0,3483 0,3121 0,2776 0,2451 0,2148 0,1867 0,1611 0,1379 0,1170 0,0985 0,0823 0,0681 0,0599 0,455 0,0367 0,0294 0,0233 0,0183 0,0143 0,0110 0,0084 0,0064 0,0048 0,0036 0,0026 0,0019 0,0014 0,0010 0,0007 0,0005 0,0003 0,0002 |
Еще одной часто используемой формой гауссова интеграла ошибок является следующая.
(Б.19)
Функции Q(x) и erfc(x) связаны следующим образом.
erfc(x) = 2Q(x
) (Б.20)
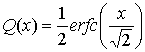(Б.21)
Литература
1. Van Trees H. L. Detection, Estimation, and Modulation Theory. Part 1, John Wiley & Sons. Inc., New York, 1968.
2. Papoulis A. Probability, Random Variables, and Stochastic Processes. McGraw-Hill Book Company, New York, 1965.