Импульсная характеристика и передаточная функция являются общими характеристиками цепи.

h(nT) – импульсная характеристика,

H(Z) – передаточная функция.

Обе характеристики связаны Z – преобразованиями.

При проектировании дискретной цепи требования к цепи задаются в виде требований импульсной характеристики цепи или передаточной функции.

Обычно схему цепи строят по известной передаточной функции. Если схема цепи известна, то импульсную характеристику можно получить одним из следующих способов:

1) непосредственно по схеме, как реакцию цепи на δ–функцию;

2) решением разностного уравнения, полагая: x(nT)= δ(nT), y(nT)=H(nT);

3) по известной передаточной функции H(Z):

a) применяя обратное Z–преобразование,

b) применяя теоремы разложения для H(Z) (аналогично определению оригинала по известному изображению),

c) делением числителя H(Z) на знаменатель с последующим применением теорем линейности и запаздывания (простой способ).

Пример простого способа: Определить h(nT), если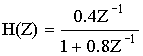

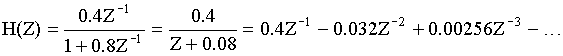
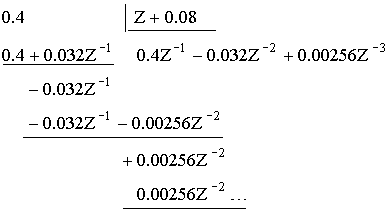
Применяя теорему линейности и запаздывания, получаем h(nT).

h(nT) = {0; 0.4; -0.032; 0.00256; …}