2.1. Отражение и преломление света на границе раздела двух диэлектрических сред

2.2. Полное внутреннее отражение

2.3. Числовая апертура

2.4. Частотное и пространственное изменения показателя преломления

2.5. Оптические волокна со ступенчатым профилем показателя преломления

2.6. Оптические волокна с градиентным профилем показателя преломления

2.7. Многоступенчатый профиль показателя преломления

2.1. Отражение и преломление света на границе раздела двух диэлектрических сред

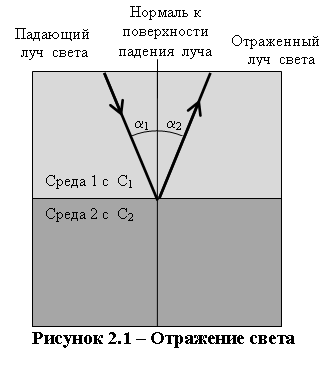
Отражение света. Когда свет падает на границу раздела двух сред, определённая его часть отражается. Количество отражённого света зависит от угла α₁ между падающим лучом света и нормалью к поверхности падения. Термин «луч света» здесь используется для обозначения пути, по которому проходит световая энергия. Для отражённого луча и угла α₂, образованного нормалью к поверхности падения и отражённым лучом света (рисунок 2.1), имеют силу следующие утверждения:

Отражённый луч:

- остаётся в плоскости падения, образуемой падающим лучом света и нормалью к поверхности падения луча;

- по отношению к падающему лучу света лежит на противоположной стороне от нормали к поверхности падения луча;

- имеет угол отражения по отношению к нормали к поверхности падения, равный углу падения.

a₁ = a_{2 .} (2.1.1)

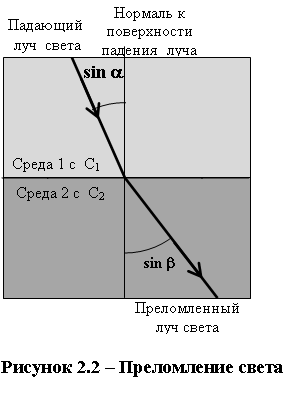
Преломление света. Когда луч света входит под углом падения α в оптически более плотную среду (например, стекло или воду) из оптически менее плотной среды (например, воздуха), то его направление распространения по отношению к нормали к поверхности падения изменяется, он преломляется под углом преломления β.

Для изотропной среды, то есть материала или вещества, имеющего одинаковые свойства во всех направлениях, применим закон преломления Снеллиуса: отношение угла падения к синусу угла преломления является величиной постоянной и также идентично отношению с₁/с₂ скоростей света с₁ в первой среде и с₂ во второй среде (рисунок 2.2)

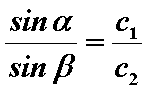, (2.1.2)

где α – угол падения; с₁– скорость света 1;

β – угол преломления; с₂– скорость света 2.

Из двух оптических сред более плотной называется та, в которой скорость света меньше.

При переходе из вакуума (воздуха), где свет распространяется со скоростью с_о, в среду со скоростью света с имеет силу отношение

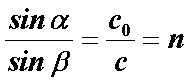. (2.1.3)

Отношение скорости света с_о в вакууме к скорости света с в среде называется показателем преломления n (более точно, фазовым показателем преломления) соответствующей среды. Показатель преломления вакуума (воздуха) n_o=1.

Для двух различных сред с показателями преломления n₁ и n₂ и скоростями света в них c₁ и c₂ имеют силу следующие соотношения:

c₁=c_o/n₁ и c₂=c_o/n_{2 .} (2.1.4)

Отсюда следует еще одна форма закона Снеллиуса - отношение синуса угла падения к синусу угла преломления равно обратному отношению соответствующих показателей преломления:

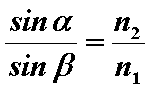. (2.1.5)

2.2. Полное внутреннее отражение

Если луч света (3) падает на поверхность раздела между средой с показателем преломления n₁ и  средой с показателем преломления n₂<n₁ под постепенно уменьшающимся углом, то есть с постепенно увеличивающимся углом падения a, то при определенном угле падения a_о угол преломления становится равным β_о = 90^о (рисунок 2.3).

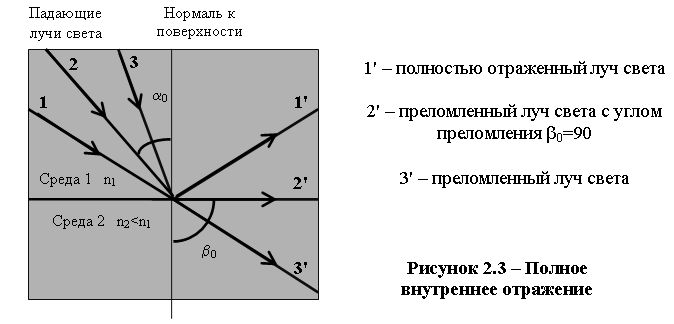
В этом случае луч света (2') распространяется параллельно поверхности раздела двух сред. Угол падения a_о называется критическим (предельным) углом двух сред.

Для критического угла a_о имеет силу следующее соотношение:

                                                   sin a_о = n₂ / n₁  ,

то есть критический угол зависит от отношения показателей преломления n₁ и n₂ двух сред.

Например, для критического угла между водой с n₁=1,333 и воздухом с n_o=1 имеем   sina_о=1/1,333 » 0,75    и    a_о » 49^о; между стеклом с n₁=1,5 и воздухом с n_o=1 он равен  sina_о=1/1,5 » 0,67    и    a_о»42^о.

Для всех лучей, у которых угол падения a больше критического угла a_о, не существует соответствующих преломленных лучей в оптически менее плотной среде. Эти лучи света отражаются на поверхности раздела обратно в оптически более плотную среду - это явление называется полное внутреннее отражение (луч света 1).

Полное внутреннее отражение может происходить на поверхности раздела сред только тогда, когда луч света распространяется из оптически более плотной среды (например, стекло n₁=1,5) в оптически менее плотную среду (например, воздух n_o=1), и никогда не происходит в обратном случае.

2.3. Числовая апертура

Эффект полного внутреннего отражения реализуется в оптических волноводах за счет того, что в середине световода имеется «стеклянная сердцевина» с показателем преломления n₁ и вокруг нее – «стеклянная оболочка» с показателем преломления n₂, при этом n₁ несколько выше n₂ (рисунок 2.4).

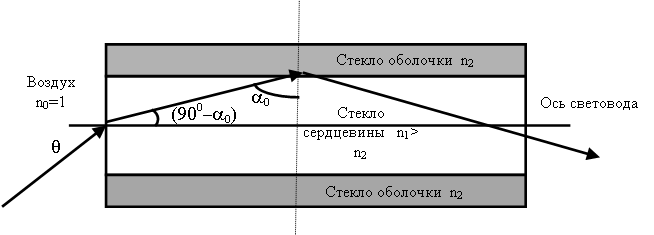
Рисунок 2.4 – Распространение света в волоконном световоде

Из требования sina_о=n₂/n₁ следует, что все лучи, отклоняющиеся от оси световода на угол не более (90^о–a₀), будут распространяться в сердцевине. Для того чтобы ввести свет снаружи (воздух с показателем преломления n₀=1) в сердцевину, угол ввода между лучом света и осью световода можно определить в соответствии с законом преломления:

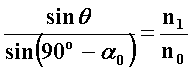                                      ,                                             (2.3.1)

и следовательно,

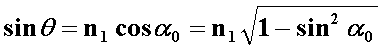                         .           (2.3.2)

С учетом требования относительно критического угла sina_о=n₂/n₁ результат будет следующим:

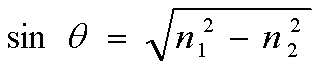                                  .              (2.3.3)

Максимальный возможный угол ввода (лучей на торец световода) q_max называется входной угловой апертурой световода. Она зависит только от двух показателей преломления: n₁ и n₂. Синус входной угловой апертуры называется числовой апертурой NA световода

                                                   .                          (2.3.4)

Эта величина очень важна для ввода света в волоконный световод.

2.4. Частотное и пространственное изменения показателя преломления

Внутри волновых пакетов отдельные волны распространяются с различными скоростями благодаря их различным длинам. Скорость распространения такого волнового пакета называется групповой скоростью. Определен и соответствующий групповой показатель преломления n_g, который соотносится с показателем преломления следующим образом

n_g = n –l ^. (2.4.1)

На рисунке 2.5 показаны кривые для n и n_g для чистого кварцевого стекла в зависимости от длины волны l.

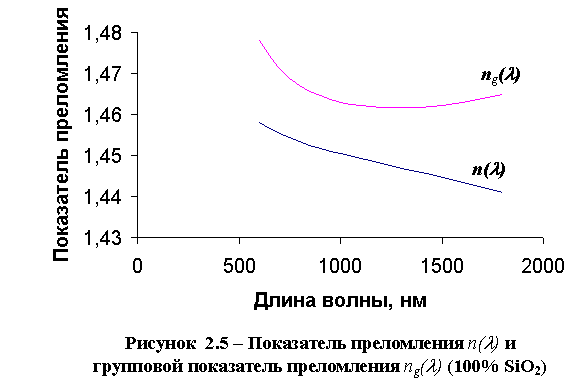
В таблице 2.1 представлены некоторые численные значения n(l) и n_g(l) для кварца.

Таблица 2.1 – Показатель преломления n(l) и групповой показатель преломления n_g(l)

Выражение dn/dl дает наклон кривой показателя преломления n(l), который в рассматриваемом диапазоне длин волн является нисходящим (отрицательным). Поэтому групповой показатель преломления n_g при любой длине волны больше показателя преломления n. Для расчетов времени передачи оптических сигналов следует использовать только групповой показатель преломления n_g.

Полезно отметить, что групповой показатель преломления достигает своего минимума вблизи длины волны 1300 нм. Этот диапазон длин волн является особенно интересным для оптической связи.

Если рассматривать показатель преломления n волоконного световода как функцию от радиуса r, то используется термин профиль распределения показателя преломления. С его помощью описывается радиальное изменение показателя преломления от оси волокна в стекле сердцевины в направлении стекла оболочки: n=n(r).

Распределение мод в волоконном световоде зависит от формы этого профиля распределения показателя преломления (рисунок 2.6).

Для практического применения важными являются «профили распределения показателя преломления, описываемые по степенному закону» (степенные профили). Под ними понимаются профили показателя преломления, у которых кривая изменения по радиусу описывается как степенная функция радиуса:

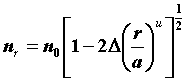, для r < a (в сердцевине) (2.4.2)

и

n²(r)=n²₂ = постоянная , для r ³ a (в оболочке) (2.4.3)

где

n₀ - показатель преломления в центре сердцевины;

n₁ - показатель преломления вдоль оси оптического волокна;

D - нормированная разность показателей преломления;

r - расстояние от оси оптического волокна, мкм;

a - радиус сердцевины, мкм;

u - показатель степени профиля;

n₂ - показатель преломления оболочки.

Нормированная разность показателей преломления соотносится с числовой апертурой NA или показателями преломления n₁ и n₂ следующим образом

D = (NA)² / 2 n²₁ = (n²₁ - n²₂) / 2 n²₁ . (2.4.4)

Отметим особые случаи (рисунок 2.6):

u = 1 – треугольный профиль

u = 2 – параболический профиль

u ®¥ – ступенчатый профиль (предел величины u - бесконечность).

Лишь в последнем случае – при ступенчатом профиле – показатель преломления n(r)=n₁ в стекле сердцевины остается постоянным. Для всех других профилей показатель преломления n(r) в стекле сердцевины постепенно увеличивается от n₂ для стекла оболочки до n₁ у оси волоконного световода.

Поэтому такие профили называют градиентными профилями распределения показателя преломления. Это название особенно хорошо закрепилось за параболическим профилем, имеющим u=2, оптические волокна с таким профилем имеют технически очень хорошие характеристики передачи света.

2.5. Оптические волокна со ступенчатым профилем показателя преломления

Для того чтобы свет направлялся в стекле сердцевины волоконного световода со ступенчатым профилем показателя преломления благодаря полному внутреннему отражению, необходимо иметь показатель преломления n₁ стекла сердцевины немного больше показателя преломления n₂ стекла оболочки на границе раздела двух стеклянных сред. Если показатель преломления n₁ одинаков по всему поперечному сечению сердцевины, то говорят, что показатель преломления  имеет ступенчатый профиль, так как при переходе от стекла оболочки к стеклу сердцевины показатель преломления возрастает ступенеобразно и остается там неизменным. На рисунке 2.7 приведены ступенчатый профиль показателя преломления волоконного световода, а также распространение луча света с соответствующими углами. Такой волоконный волновод называется световодом со ступенчатым профилем показателя преломления или ступенчатым световодом. Этот тип волоконного световода легко изготовить. Однако в настоящее время он применяется довольно редко. Для того чтобы лучше проиллюстрировать распространение света в таком световоде, выбран нижеследующий пример (рисунок 2.7).

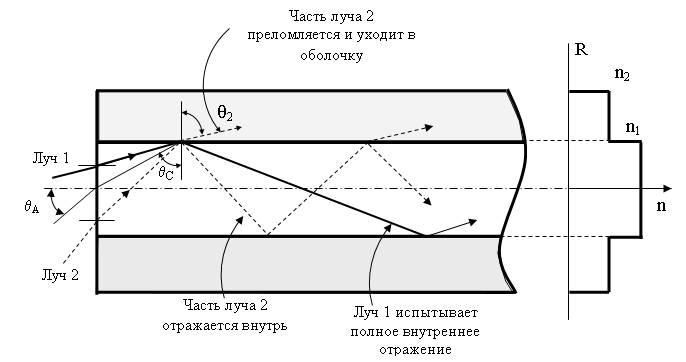
Рисунок 2.7 - Ход лучей в многомодовом оптическом волокне

Типичные размеры многомодового световода со ступенчатым профилем показателя преломления:

- диаметр сердцевины    2а = 100 мкм;

- диаметр оболочки       D = 140 мкм;

- показатель преломления сердцевины  n₁= 1,48;

- показатель преломления оболочки         n₂ = 1,46.

В этом случае для критического угла a_о  полного внутреннего отражения, то есть наименьшего угла к нормали падения, при котором луч света направляется в стекле сердцевины и не преломляется в стекле оболочки, справедливы

           sina_о=n₂/n₁=1,46/1,48 » 0,9865;              a_о  = 80,6^o.                           (2.5.1)

Все лучи света, которые образуют угол с осью волоконного световода £ (90^о - a_о) = 9,4^о, распространяются в стекле сердцевины.

Когда свет вводится в стекло сердцевины снаружи (воздух n_o = 1), то следует учитывать закон преломления, так как свет может войти в оптическое волокно только в пределах определенного апертурного угла q. В таком случае справедливо

           ; q»14,0^о  .         (2.5.2)

Такой волоконный световод является многомодовым. Импульс света, распространяющийся в нем, состоит из многих составляющих, направляемых в отдельных модах световода. Каждая из этих мод возбуждается на входе волновода под своим определенным углом ввода и направляется по нему в пределах стекла сердцевины соответственно по различным траекториям движения луча. Каждая мода проходит разное расстояние оптического пути и поэтому приходит на выход световода в разное время. Наибольшее время прохождения соотносится с меньшим временем прохождения так же, как соотносятся показатели преломления стекла сердцевины и оболочки, и поэтому такое отношение имеет величину того же порядка, что и нормированная разность показателей преломления D, то есть выше 1%.

Эта модовая дисперсия может быть полностью исключена, если структурные параметры ступенчатого световода подобрать таким образом, что в нем будет направляться только одна мода, а именно – фундаментальная (основная) мода HE₁₁.

Однако основная мода также уширяется во времени по мере ее прохождения по такому световоду. Это явление называется хроматической дисперсией (раздел 5.3). Поскольку она является свойством материала, она, как правило, имеет место в любом оптическом световоде. По сравнению с дисперсией мод хроматическая дисперсия в диапазоне длин волн от 1200 до 1600 нм относительно мала или отсутствует.

Чтобы описать размер (радиальную амплитуду поля) фундаментальной моды, был введен термин диаметр поля моды 2w_o (раздел 3.5). Для изготовления ступенчатого волоконного световода с малым затуханием, который направляет только фундаментальную моду в диапазоне длин волн более 1200 нм, диаметр поля моды 2w_o должен быть уменьшен до 10 мкм. Такой ступенчатый волоконный световод называется одномодовым оптическим волокном.

Здесь полезно отметить, что не только диаметр сердцевины, но и числовая апертура и вследствие этого также входная угловая апертура намного меньше, чем соответствующие параметры у многомодового ступенчатого световода, что делает относительно трудным введение света в одномодовый световод.

Если одномодовые световоды имеют изгибы или соединения, то размер диаметра поля моды является важным фактором, влияющим на характеристики затухания. Так, увеличение диаметра поля моды приводит к ухудшению пропускания света в изгибах, но уменьшает потери в разъемных и неразъемных соединениях.

2.6. Оптические волокна с градиентным профилем показателя преломления

В многомодовом ступенчатом световоде моды распространяются по оптическим путям различной длины и поэтому приходят к концу световода в разное время. Эта нежелательная модовая дисперсия может быть значительно уменьшена, если показатель преломления стекла сердцевины уменьшается параболически от максимальной величины n₀ у оси световода до величины показателя преломления n₂ на поверхности раздела с оболочкой. Такой градиентный профиль показателя преломления или профиль показателя преломления, описываемый по степенному закону, с показателем степени профиля u=2 характеризуется уравнениями:

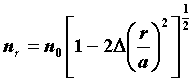           ,    для r<a в сердцевине                               (2.6.1)

           n²(r)=n²₂  ,                          для r>a в оболочке                                  (2.6.2)

Оптический волновод с таким градиентным профилем показателя преломления также называется градиентным волоконным световодом.

Типичные размеры световода с градиентным профилем показателя преломления

- диаметр сердцевины    2а = 50 мкм;

- диаметр оболочки        D = 125 мкм;

- максимальный показатель преломления сердцевины n₁ = 1,46;

- разность показателей преломления         D = 0,010.

На рисунке 2.8 представлены ход световых волн различного порядка и профиль показателя преломления градиентного световода.

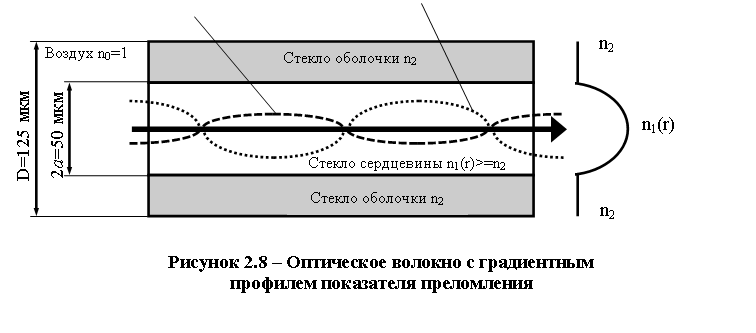
Лучи света проходят по оптическому волокну по волно- и винтообразным спиральным траекториям. В противоположность ступенчатому профилю показателя преломления, они распространяются уже не зигзагообразно. Вследствие непрерывного изменения показателя преломления n(r) в стекле сердцевины лучи непрерывно преломляются, и поэтому их направление распространения меняется, за счет чего они распространяются по волновым траекториям. Лучи, колеблющиеся вокруг оси волновода, проходят более длинный путь, чем луч света вдоль оси световода. Однако, благодаря меньшему показателю преломления в отдалении от оси оптического волокна эти лучи распространяются соответственно быстрее, благодаря чему более длинные оптические пути компенсируются меньшим временем прохождения. В результате различие временных задержек разных лучей почти полностью исчезает. При точном изготовлении параболического профиля показателя преломления разность временных задержек по результатам измерений в градиентном световоде составляет немногим более 0,1 нс при времени прохождения света 5 мкс на расстоянии 1 км.

Эта незначительная разница временных задержек в градиентных световодах обуславливается, наряду с дисперсией материала, дисперсией профиля. Она возникает вследствие того, что показатели преломления сердцевины и оболочки изменяются по мере изменения длины волны l по-разному, поэтому разность показателей преломления D и показатель степени профиля u зависят от длины волны. Оптимальный показатель степени параболического градиентного профиля может быть теоретически рассчитан по формуле

                                                     U_опт=2–2P-D(2-P) ,                             (2.6.3)

причем как параметр Р<<1, так и разность показателей преломления D зависят от длины волны l, и поэтому показатель степени профиля u также зависят от длины волны.

Отсюда профиль показателя преломления градиентного световода при u»2 делает возможным, чтобы все направления моды имели почти одинаковую временную задержку лишь в ограниченном диапазоне длин волн.

Поскольку показатель преломления n₁(r) градиентного волоконного световода зависит от расстояния r от оси световода, то числовая апертура, играющая важную роль для ввода света в сердцевину, является функцией r:

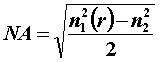                                                   .                                      (2.6.4)

Для типичного световода с градиентным профилем показателя преломления числовая апертура равна

                             ,                           (2.6.5)

и максимальная входная угловая апертура q_max у оси световода равна

           sinq_max=NA » 0,206;                           q_max  » 11,9^o.                     (2.6.6)

2.7. Многоступенчатый профиль показателя преломления

Дисперсия в одномодовом волоконном световоде состоит из дисперсии двух типов. С одной стороны, существует дисперсия материала, вызываемая зависимостью показателя преломления и, следовательно, скорости света от длины волны n=n(l) (рисунок 2.5), c=c(l). С другой стороны, существует волноводная дисперсия, возникающая в результате зависимости распределения света фундаментальной моды НЕ₁₁ по стеклу сердцевины и оболочки (рисунок 4.5) и, следовательно, разности показателей преломления от длины волны: D=D(l). Оба типа дисперсии, вместе взятые, называются хроматической дисперсией. В диапазоне длин волн более 1300 нм эти два типа дисперсии в кварцевом стекле имеют противоположные знаки. Дисперсия материала может быть изменена лишь незначительно с помощью других легирующих добавок. Напротив, волноводная дисперсия может быть подвержена сильному влиянию за счет использования другой структуры профиля показателя преломления.

Профиль показателя преломления обычного одномодового световода бывает ступенчатым с разностью показателей преломления D. Для такой простой структуры профиля сумма дисперсии материала и волноводной дисперсии при длине волны l=1300 нм равна нулю.

Если желательно иметь нулевую дисперсию при других длинах волн, то необходимо изменить волноводную дисперсию и, следовательно, структуру профиля волоконного световода. Это приводит к многоступенчатому или сегментному профилю показателя преломления. Используя эти профили, можно производить волоконные световоды, у которых длина волны с нулевой дисперсией сдвинута до 1550 нм (так называемые волоконные световоды со сдвинутой дисперсией) или величины дисперсии очень малы во всем диапазоне длин волн от 1300 до 1550 нм (так называемые волоконные световоды со сглаженной дисперсией или волоконные световоды с компенсированной дисперсией).

Контрольные вопросы 1.  Почему на практике применяется волоконный световод, состоящий из сердцевины и оболочки? 2.  Что такое «профиль показателя преломления волоконного световода»? 3.  Какой волоконный световод (оптическое волокно) называется ступенчатым и какой градиентным? 4.  Дайте определение числовой апертуры волоконного световода; чем она отличается от действительной числовой апертуры? 5.  Какие материалы используют для изготовления волоконных световодов? 6.  Что понимают под «оптимальным профилем» показателя преломления градиентного световода? 7.  Нарисуйте картину преломления света. Изобразите падающий луч, преломленный луч и нормаль к поверхности раздела двух диэлектрических сред. 8.  Нарисуйте картину отражения света. Изобразите падающий луч, отраженный луч и нормаль к поверхности раздела двух диэлектрических сред. 9.  Где скорость света больше: в воздухе или в стекле? 10.  В соответствии с каким принципом свет распространяется вдоль волокна со ступенчатым профилем показателя преломления? 11.  Как называется волокно с перемsенным показателем преломления сердцевины? 12.  Охарактеризуйте процесс распространения оптических сигналов с точки зрения геометрической оптики.