При передаче цифровых данных по каналу с шумом и, тем более, с замираниями, обусловленными многолучевым распространением радиоволн, всегда существует вероятность того, что принятые данные будут содержать ошибки. Частота появления ошибок, при превышении которой принятые данные использовать нельзя, определяется свойствами слухового восприятия человека. А именно - должна быть установлена допустимая вероятность ошибок Р_ош, не приводящая к заметным на слух искажениям на аналоговом выходе. Поэтому средняя вероятность ошибочного приема элемента сигнала Р_ош является основной характеристикой помехоустойчивости цифрового канала связи. Снижение вероятности ошибок может быть достигнуто путем повышения требований к энергетическим характеристикам радиосистемы передачи – мощности радиопередатчиков, коэффициенту усиления антенн, шумовой температуре приемников. Однако далеко не всегда эти меры экономически оправданы и позволяют снизить вероятность ошибок до пренебрежимо малой величины.

Одним из важнейших средств в обеспечении достоверности передачи цифровых данных является использование канального кодирования с исправлением ошибок (FEC coding). Кодирование канала (иначе – избыточное или помехоустойчивое кодирование), основанное на применении специальных корректирующих кодов, реализуется путем добавления по определенному алгоритму в каждый кодовый блок некоторого количества поверочных символов. Эта избыточность позволяет корректирующему ошибки декодеру детектировать и исправлять неверно дошедшие данные и восстанавливать исходный поток данных по принятому потоку.

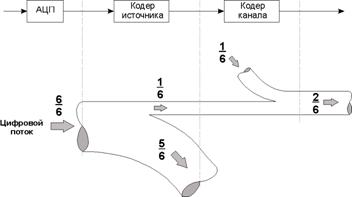
Рис. 15.1. Иллюстрация процессов кодирования источника и канала

Выбор типа корректирующего кода и его параметров зависит от требуемой достоверности приема, допустимой скорости передачи, вида ошибок в канале, сложности (стоимости) реализации схем декодирования. Учитывается также, что в результате эффективного устранения избыточности в процессе кодирования источника, предшествующего кодированию канала, информационная ценность каждого передаваемого в канал бита резко возрастает. Приблизительное соотношение естественной избыточности речевого сигнала и искусственной избыточности, вносимой в канал кодером канала, иллюстрирует рис. 15.1.

Обсудим простые модели канала, описывающие процессы, происходящие между кодером и декодером (см. также рис. 6.1). На рис. 15.2 представлено несколько базовых моделей каналов, применимых для анализа канального кодирования. Наиболее простая модель называется двоичным симметричным каналом (ДСК) без памяти (рис. 15.2,а). Входы и выходы этого канала - двоичные. Переданные и принятые блоки данных соблюдают побитовый порядок и на входе, и на выходе модели канала. Каждый бит кодируемой последовательности приходит на выход канала в неизменном виде с вероятностью 1 – Р_ош. С вероятностью Р_ош передаваемые биты инвертируются, т.е. возникают битовые ошибки. Декодер принимает решение о переданной закодированной последовательности с по принятой двоичной последовательности г. В процессе принятия решения декодером могут применяться только те отношения алгебраической независимости между отдельными битами переданной последовательности, которые были установлены правилом кодирования. Отсутствие у рассматриваемой модели памяти приводит к тому, что ошибки статистически становятся взаимно независимыми, т.е. возникновение ошибок в предшествующие моменты времени никак не влияет на вероятность появления ошибок в текущий момент.

Очень немногие реальные каналы передачи могут считаться действительно не имеющими памяти. В большинстве случаев ошибки возникают пакетами. С другой стороны, существует множество алгоритмов декодирования, разработанных специально для исправления случайных ошибок, т.е. ориентированных на каналы без памяти. С целью обеспечения достаточно высокой эффективности коррекции ошибок предпринимаются дополнительные меры для разбиения пакетов ошибок в приемнике, в частности, метод перемежения (interleaving) данных.

Вторая модель канала (рис. 15.2,б) учитывает пакетную природу ошибок, возникающих в канале передачи данных. Это значит, что появление одной ошибки в конкретный момент времени увеличивает вероятность появления ошибки в следующий момент. В этом случае говорят, что канал обладает памятью о своих предыдущих состояниях. Для таких ситуаций разработаны специальные коды и алгоритмы декодирования.

В третьей модели (рис. 15.2,в), которая аналогично первой не имеет памяти, декодер использует не только знания об алгебраических соотношениях между отдельными битами, но и дополнительную информацию, поступающую из канала и позволяющую оптимизировать процесс декодирования. Для получения такой информации отсчет сигнала, полученный в приемнике в процессе демодуляции, квантуется в М-уровневом квантователе.

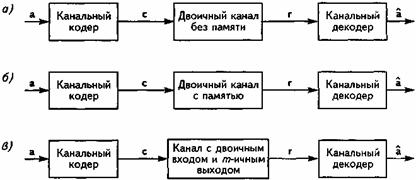
Рис. 15.2. Модели каналов с точки зрения канального кодирования

Если каждому возможному уровню квантования поставить в соответствие число от 0 до М – 1, то будет получена модель канала с двоичным входом и т-ичным выходом (рис. 15.3). В такой модели сигнал на выходе канала измеряется намного точнее, чем в модели двоичного канала. Это позволяет использовать дополнительную информацию, содержащуюся в принятом символе для повышения качества декодирования, т.е. снизить вероятность принятия неверного решения о принимаемой кодированной последовательности. Декодирование, при котором используется дополнительная информация канала, называется декодированием с мягким решением. В противовес ему, декодирование с использованием только информации двоичных символов называется декодированием с жестким решением. В большинстве применяемых в современной цифровой сотовой телефонии алгоритмов декодирования используются мягкие решения.

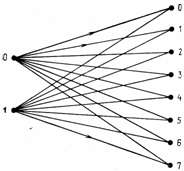
Рис. 15.3. Модель двоичного канала, обеспечивающего мягкие решения при M = 8.

В современных цифровых системах связи и вещания для обнаружения и исправления ошибок применяют либо блочные (блоковые) корректирующие (n,k)-коды, либо сверточные коды (СК). Определяющее различие между кодерами для кодов этих двух типов состоит в наличии или отсутствии памяти.

Кодер для блокового кода отображает последовательности из k входных символов в последовательности из n выходных символов, причем всегда п > k.. При этом каждый блок из n символов зависит только от соответствующего блока из k символов и не зависит от других блоков. Параметрами блокового кода являются n, k, R = k/n – скорость кода и d - кодовое расстояние. Кодовое расстояние является основным показателем корректирующей способности кода. Оно равно минимальному числу позиций, в которых кодовые комбинации отличаются друг от друга. Если в пределах блока кода при передаче появляется q ошибочных символов, то считают, что произошла ошибка кратности q. Кратность обнаруживаемых q_о и исправляемых q_и кодом ошибок связаны с кодовым расстоянием соотношением d = q_о + q_и + 1, причем всегда q_о ³ q_и. Конкретный тип кода задается тремя параметрами: n, k и d. При q > 3…5 эффективность блоковых кодов заметно снижается, то есть существенно возрастает требуемая при этом избыточность. Поэтому в современных СПРС используются более эффективные сверточные коды.

Сверточный код - это линейный рекуррентный код. В общем случае он образуется следующим образом. В каждый тактовый момент времени на вход кодирующего устройства (регистр сдвига с K ячейками) поступает m символов сообщения; n выходных символов формируются с помощью рекуррентного соотношения из K = m + q символов сообщения, среди которых m поступили в данный тактовый момент времени, а q - в предшествующие. Символы сообщения, из которых формируются выходные символы, хранятся в памяти кодера. Параметр K часто называют длиной кодового ограничения данного кода. СК характеризуются также скоростью R = m / n и свободным расстоянием d_св, аналогичным параметру d блоковых кодов. Типичные значения параметров СК: m,n = 1 - 8, R = 1/4 - 7/8, K = 3 -10.

Введение при кодировании канала в информационный сигнал избыточных символов сопровождается негативным эффектом — снижением, при неизменной скорости цифрового потока (R_ц), скорости передачи полезной нагрузки (С_ц) обратно пропорционально скорости кода (R): R_ц = С_ц / R, бит/с. Поэтому для сохранения скорости передачи полезной нагрузки необходимо расширение полосы частот канала в R раз или повышение кратности модуляции.

Положительным эффектом помехоустойчивого кодирования является либо снижение вероятности ошибки, либо снижение энергетики передачи при той же вероятности ошибки, либо и то, и другое одновременно. Таким образом, кодирование расширяет возможности компромисса между полосой и энергетикой канала, присущего любой системе связи.

Обычно качество системы связи характеризуется отношением энергии, приходящейся на один информационный символ, к односторонней спектральной мощности шума, т.е. отношением сигнал-шум (ОСШ) h₀ = Е_б / N₀, которое требуется для достижения заданной вероятности ошибки Р_ош. Уменьшение ОСШ (при заданном уровне Р_ош), достигнутое благодаря кодированию канала, характеризует энергетический выигрыш кодирования (ЭВК). При использовании блочных кодов величина ЭВК (при Р_ош» 1´10^-5), как правило, не превышает 2,5...3,5 дБ. Применение сверточных кодов декодируемых по алгоритму Витерби с мягкими решениями позволяет получить оценку для ЭВК 4…6 дБ.

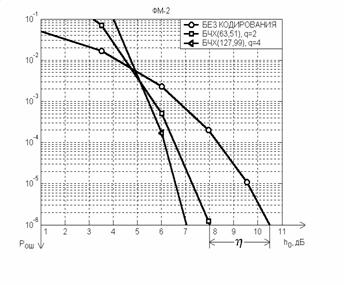
Рис. 15.4. Кривые помехоустойчивости ФМ канала с кодированием

При применении конкретного кода величина ЭВК легко находится по кривым помехоустойчивости, представляющим собой зависимости вероятности ошибки декодирования Р_ош от ОСШ на входе демодулятора. Реально достижимый ЭВК зависит, в первую очередь, от свойств корректирующего кода и алгоритма его декодирования. В качестве примера на рис. 15.4 кривые помехоустойчивости построены для двух вариантов кода БЧХ в канале с ФМ-2 при использовании жестких решений в корреляционном демодуляторе.

Определение ЭВК осуществляется относительно кривой помехоустойчивости для ФМ канала без кодирования (R=1) - при приемлемом пользователю допустимом долговременном уровне ошибок на бит информации после декодирования (Р_ош)_доп, не приводящем к заметным на слух искажениям на аналоговом выходе. Из построений следует, что при (Р_ош)_доп = 1´10^-6 (63,51)-код, обнаруживающий и исправляющий двукратные (q=2) ошибки, обеспечивает ЭВК h » 2,5 дБ, а (127,99)-код при q = 4 - выигрыш h » 3,5 дБ.

Кодирование канала сопровождается двумя весьма простыми, но чрезвычайно эффективными процедурами – перемежением символов и скремблированием цифровых потоков. Использование перемежения как одного из основных методов повышения верности передачи дискретных сообщений в каналах с группирующимися ошибками является характерной особенностью сотовой связи. Это следствие неизбежных глубоких замираний сигнала в условиях многолучевого распространения, которое практически всегда имеет место, особенно в условиях плотной городской застройки. При этом группа следующих один за другим символов, попадающих на интервал замирания (провала) сигнала, с большой вероятностью оказывается ошибочной. Если же перед выдачей информационной последовательности в радиоканал она подвергается процедуре перемежения, а на приемном конце восстанавливается прежний порядок следования символов, то пакеты ошибок с большой вероятностью рассыпаются на одиночные ошибки. Таким образом, простое перемежение (перестановка во времени) символов позволяет декоррелировать ошибки в канале, то есть преобразовать пакеты ошибок большой кратности в одиночные, сведя, в первом приближении, канал с памятью к ДСК без памяти.

Скремблирование (рандомизация), предваряя кодирование канала, превращает цифровой сигнал в квазислучайный. Это, с одной стороны, позволяет создать в цифровом сигнале достаточно большое число перепадов уровня и обеспечить самосинхронизацию - возможность выделения из него тактовых импульсов, а с другой - приводит к более равномерному энергетическому спектру излучаемого радиосигнала. Благодаря этому повышается эффективность работы передатчика и минимизируется мешающее действие радиосигнала цифровой системы передачи по отношению к аналоговым сигналам, излучаемым другими передатчиками в том же частотном диапазоне. Собственно рандомизация осуществляется путем сложения по модулю 2 исходного транспортного потока данных с выхода мультиплексора кодера речи и двоичной псевдослучайной последовательности.