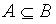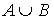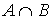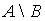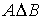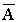1.1. Множества и отношения. Множества и элементы множеств

1.2. Сравнение множеств

1.3. Операции над множествами

1.4. Диаграммы Эйлера-Венна

1.5. Табличный способ задания множеств

1.6. Свойства операций над множествами

1.7. Отношения

1.8. Специальные бинарные отношения

1.1. Множества и отношения

Множества и элементы множеств

Определение. Множество – любая определенная совокупность объектов произвольной природы. Обозначают множества прописными латинскими буквами: A, B, ¼ , а его элементы обозначаются строчными латинскими буквами: a, b, ¼.

Например:

( является элементом множества (" принадлежит A")),

( не является элементом множества A).

Определение. Пустое множество – это множество, не содержащее ни одного элемента, обозначается оно символом: Æ.

Определение. – универсальное множество (универсум) – множество, из которого берутся элементы в конкретном рассуждении. – множество, рассматриваемое как наиболее общее в данной ситуации.

Множество элементов , удовлетворяющих свойству P(x) обозначается .

Примеры.

– множество натуральных чисел;

– множество вещественных чисел.

– множество комплексных чисел.

1.2. Сравнение множеств

Определение. (А содержится в В или В включает А), если . А называется подмножеством В. Если и 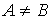, то А называется строгим (собственным) подмножеством В. Обозначается это .

Определение. 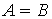если они являются подмножествами друг друга, то есть или

Определение. Мощность конечного множества – число его элементов. Мощность бесконечного множества равна ¥.

1.3. Операции над множествами

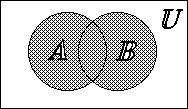
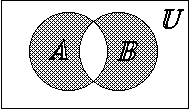
Определение. Объединением множеств А и В () называется множество, состоящее из элементов, принадлежащих хотя бы одному из них.

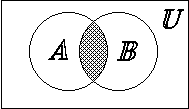
Определение. Пересечением множеств А и В () называется множество, состоящее из элементов, принадлежащих и первому и второму одновременно.

Определение. Разностью множеств А и В () называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Определение. Симметрической разностью множеств А и В () называется множество, состоящее из элементов множества А, не являющихся элементами множества В и элементов множества В, не являющихся элементами множества А.

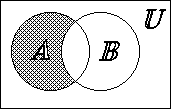
Определение. Дополнением множества А () называется множество, состоящее из элементов множества U, не принадлежащих множеству А.

Пример:

зависит от того, какое U. Если , то , если , то .

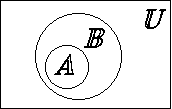
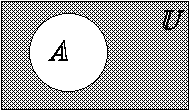
1.4. Диаграммы Эйлера-Венна

Диаграммы Эйлера-Венна – это геометрическое представление множеств. Множество U изображается прямоугольником, рассматриваемые множества – фигурами (окружностями). Для выделения результата применяется штриховка.

1.5. Табличный способ задания множеств

Пусть задано множество U. Рассмотрим произвольное его подмножество и элемент .

Определение. Индикаторной (характеристической) функцией для множества A называется функция
.

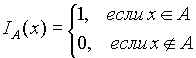Таким образом: .

Для имеют место свойства:

;

Индикаторы удобно задавать с помощью таблиц:

0 0 1 1	0 1 0 1	0 1 1 1	0 0 0 1	0 0 1 0	1 1 0 0	0 1 1 0

1.6. Свойства операций над множествами

Объединение и пересечение:

1. = – коммутативность

2. = – коммутативность

3. – ассоциативность

4. – ассоциативность

5. – дистрибутивность

6. – дистрибутивность

7. 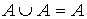– идемпотентность

8. 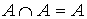– идемпотентность

9. – свойство дополнения

10. – свойство дополнения

11. – закон де Моргана

12. – закон де Моргана

13. – свойство нуля

14. – свойство нуля

Дополнение:

15. – инволютивность

16.

17.

Разность, симметрическая разность:

18.

19.

20.

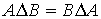
21.

22.

23.

1.7. Отношения

Определение. Пусть A и B произвольные множества. Декартовым произведением множеств A и B называется множество всевозможных упорядоченных пар, в которых первый элемент принадлежит множеству A, а второй – множеству B.

Пример. – точки плоскости.

Свойства декартовых произведений

1.

2.

3.

4.

5.

6.

Понятие отношения.

Отношение это один из способов задания взаимосвязей между элементами множества.

Унарные (одноместные) отношения отражают наличие какого-либо признака R у элемента множества A. Например, "быть четным" на множестве натуральных чисел. Все элементы множества A, отличающиеся признаком R , образуют подмножество множества A, называемое отношением R.

Бинарные отношения

Бинарные (двуместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множеств A и B. Все пары элементов множеств A и B, находящиеся в отношении R , образуют подмножество множества .

Определение. Бинарное отношение – это тройка множеств , где – график отношения. Пишут или aRb.

Область определения : ;

Область значений: ;

Обратное отношение: ;

Композиция отношений и :

.

Частичным порядком (пишут ), если оно рефлексивно, антисимметрично и транзитивно.

1.8. Специальные бинарные отношения

Бинарное отношение на A называется

1. Рефлексивным, если ;
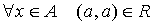2. Симметричным, если ;
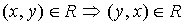3. Транзитивным, если ;
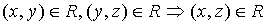4. Антисимметричным, если ;
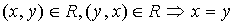5. Отношением эквивалентности на 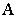(пишут 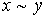), если оно рефлексивно, симметрично и транзитивно;

Определение. Бинарное отношение называется функцией из в , если и .

Функция называется

1. Сюръективной, если ;
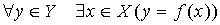2. инъективной, если ;
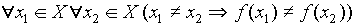3. биективной, если она сюръективна и инъективна.