Интеграл Дюамеля может быть получен, если аппроксимировать приложенное воздействие f₁(t) с помощью единичных функций, сдвинутых относительно друг друга на время Dt (рис. 8.2).

Реакция цепи на каждое ступенчатое воздействие определится как

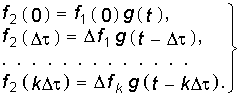
Результирующая реакция цепи на систему ступенчатых воздействий найдется, исходя из принципа наложения:

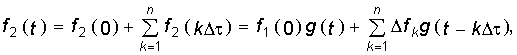
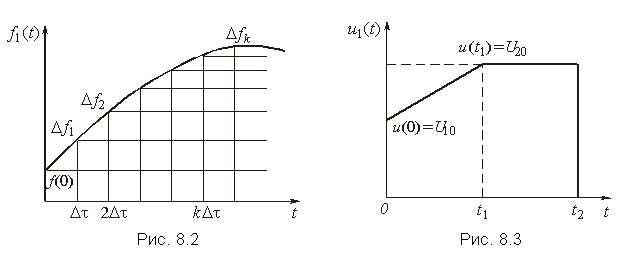
где п — число аппроксимирующих участков, на которые разбит интервал 0 ... t. Домножив и разделив выражение, стоящее под знаком суммы, на Dt и перейдя к пределу с учетом того получим одну из форм интеграла Дюамеля: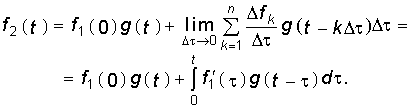

Уравнение (8.8) отражает реакцию цепи на заданное воздействие, поскольку аппроксимирующая функция стремится к исходной.

Вторая форма интеграла Дюамеля может быть получена с помощью теоремы свертки:

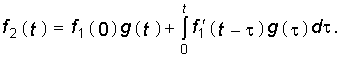
Наконец, интегрируя по частям выражения, стоящие в уравнениях (8.8) и (8.9), получаем третью и четвертую формы интеграла Дюамеля:

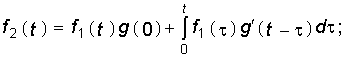
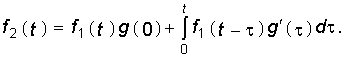
Применение той или иной формы интеграла Дюамеля диктуется удобством и простотой вычисления подынтегральных выражений.

Пример. Запишем реакцию цепи (см. рис. 8.1) на напряжение, изображенное на рис. 8.3 с помощью интеграла Дюамеля (8.8). Переходная характеристика данной цепи имеет вид .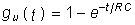

После нахождения переходной функции определяем число участков интегрирования, где функция непрерывна и дифференцируема. Определяем значение 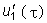на этих участках. Для рассматриваемого воздействия таких участков будет три: 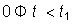, , 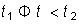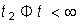. Необходимость включения третьего участка объясняется тем обстоятельством, что несмотря на прекращение входного воздействия в силу переходных процессов в цепи будет наблюдаться остаточная реакция. Для каждого из выделенных участков запишем уравнение (8.8) с учетом реакций предыдущих участков:

на участке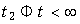

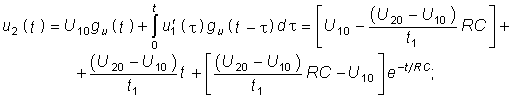
на участке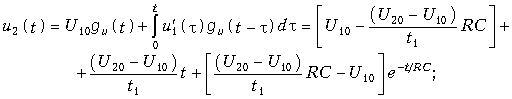

на участке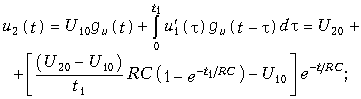

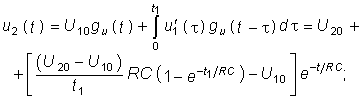
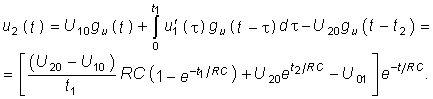
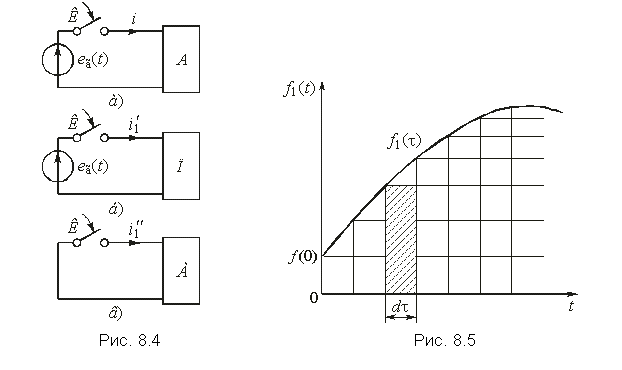
В случае, когда воздействие прикладывается к активной цепи (рис. 8.4, а), расчет переходных процессов можно вести методом наложения. При этом вначале расчет ведется с помощью интеграла Дюамеля для пассивной цепи (рис. 8.4, б), затем определяется классическим или операторным методом реакция цепи при включении рассматриваемой ветви к активному двухполюснику (рис. 8.4, в). Результирующая реакция находится как сумма реакций: 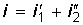.