В теории информации чаще всего необходимо знать не количество информации I(xi), содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.

Если имеется ансамбль (полная группа) из k сообщений x1, x2 ... xi, xk с вероятностями p(xi) ... p(xk), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений H(x), определяется формулой

(2) или (3)

Размерность энтропии - количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения.

Рассмотрим свойства энтропии.

1. Чем больше неопределённость выбора сообщений, тем больше энтропия. Неопределённость максимальна при равенстве вероятностей выбора каждого сообщения: p(x1)=p(x2)= . . .=p(xi)=1/k.

В этом случае

(4) (т.е. максимальная энтропия равна логарифму от объёма алфавита).

Например, при k=2 (двоичный источник) бит.

2. Неопределённость минимальна, если одна из вероятностей равна единице, а остальные - нулю (выбирается всегда только одно заранее известное сообщение, например, - одна буква): p(x1)=1; p(x2)= p(x3)= ... = p(xk)= 0. В этом случае H(x)=Hmin(x)=0.

Эти свойства энтропии иллюстрируются следующим образом.

Пусть имеется двоичный источник сообщений,

т.е. осуществляется выбор всего двух букв (k=2): x1 и x2, p(x1)+ p(x2)= 1. Тогда

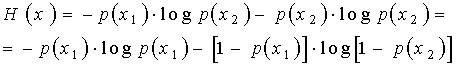(5)

Зависимость H(x) от вероятностей выбора для двоичного источника приведена на рис. 1.

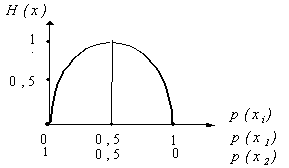
Рис. 1

3. Укрупним алфавит. Пусть на выходе двоичного источника имеется устройство, которое группирует буквы в слова из n букв. Тогда k = 2n слов (объём алфавита). В этом случае бит. (6)

Таким образом, укрупнение алфавита привело к увеличению энтропии в n раз, так как теперь уже слово включает в себя информацию n букв двоичного источника. Тем самым доказывается свойство аддитивности энтропии.

4. Энтропия дискретного источника не может быть отрицательной.

Термин “энтропия” заимствован из термодинамики и применительно к технике связи предложен американским учёным К.Шенноном, в трудах которого были заложены основы теории информации (математической теории связи).

Вопросы

1. Что такое энтропия источника с независимым выбором сообщений?
2. Как определяется энтропия дискретного источника с независимым выбором сообщений? Размерность энтропии источника.
3. Когда энтропия дискретного источника максимальна и чему она равна?
4. Когда энтропия дискретного источника минимальна (в частности, когда она равна нулю)?
5. Чему равна энтропия источника при укрупнении алфавита( при объединении букв в слова)?