При выборе электронного режима генераторной лампы стремятся от неё получить необходимую величину колебательной мощности при высоком электронном КПД. Энергетические показатели генератора зависят от первой гармоники и постоянной составляющей импульса анодного тока, которые могут быть определены если известен импульс анодного тока при заданных напряжениях, действующих на электродах лампы. Эта задача может быть решена, если известны зависимости анодного тока от параметров лампы и от приложенных к ней напряжений. Однако, анодный ток в лампе выражается сложной функцией этих напряжений . Эта функция не имеет точного аналитического выражения, поэтому расчет электронного режима генератора можно выполнить либо при графическом представлении реальных вольтамперных статических характеристик лампы, либо аналитическим методом при определенной идеализации реальных характеристик.

Графический метод расчета генератора является весьма трудоемким, так как при этом приходится рассчитывать не один, а целую серию режимов генераторной лампы при различных нагрузках, а затем уже определить наиболее благоприятный режим.

При аналитическом методе расчета идеализируют реальные статические характеристики лампы, находят выражение для анодного тока и вычисляют его гармонические составляющие. Наибольшее распространение получила квазилинейная теория лампового генератора, созданная А.И. Бергом. Её сущность заключается в следующем.

1. Предполагается, что добротность нагруженного анодного контура достаточно высокая (Q_н>>1) и можно считать, что при действии на сетке лампы напряжения

на анодном контуре генератора, настроенном в резонанс на рабочую частоту w, имеет место падение напряжения только частоты w. При этом напряжение на аноде лампы равно:

Тогда анодный ток является функцией:

2. Криволинейные участки реальных характеристик лампы заменяют отрезками прямых (ломаных) линий, которые хорошо с ними совмещаются.

3. Статические параметры лампы, крутизну S и внутреннее сопротивление R_i, заменяют средними за период высокой частоты параметрами, зависящими от положения рабочей точки лампы, её электронного режима и характера нагрузки.

Благодаря кусочно-линейной аппроксимации статических характеристик лампы, процессы, происходящие в генераторе, описываются простыми линейными уравнениями и, главное - при косинусоидальной форме напряжения возбуждения в цепи управляющей сетки анодный ток представляет собой периодическую последовательность импульсов также косинусоидальной формы, что позволяет использовать для определения их гармонических составляющих разложение в ряд Фурье, согласно которому любая гармоника такого импульса определяется простой формулой:

I_n= a_n i_max , … (1.3)

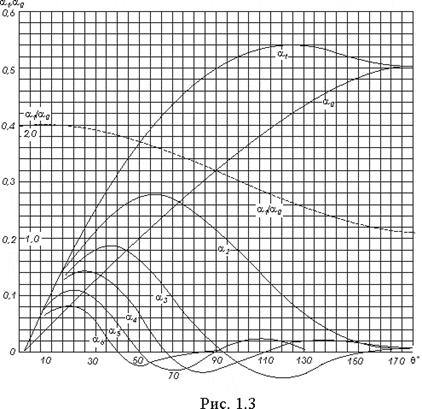
где a_n - коэффициенты разложения периодической последовательности остроконечных косинусоидальных импульсов, которые табулированы. Таким образом, для расчёта гармонических составляющих импульса достаточно вычислить его угол отсечки q и максимальное значение i_max.

Можно показать, что при линейной аппроксимации характеристик лампы суммарный ток описывается выражением:

i_s = S(e_g– E_g0 + De_a) , …(1.4)

где e_g и e_а описываются выражениями (1.1) и (1.2), D-проницаемость и S- крутизна лампы - статические параметры лампы (как известно, SDR_i=1, где R_i - внутреннее сопротивление лампы), a E_g0 - напряжение сеточного приведения, при котором в системе координат (i_s,e_g) идеализированная характеристика суммарного тока, соответствующая анодному напряжению Е_а=0, пересекает ось абсцисс. Из (1.4) следует, что суммарный ток практически не зависит от анодного напряжения, поскольку проницаемость D ламп очень мала: у триодов она порядка 10^-2 , а у экранированных ламп - порядка 10^-3. При работе генератора в недонапряженном и критическом режимах можно считать, что анодный ток равен суммарному. Тогда, подставляя в (1.4) выражения (1.1) и (1.2) для e_g и e_а и производя несложные преобразования, получим формулы для максимального значения импульса анодного тока i_amax и косинуса его угла отсечки q:

i_amax=S(1-cosq)(U_g-DU_к) , … (1.5)

cosq = , … (1.6)

где U_к = I_a1R_э – напряжение на анодном контуре, R_э – его эквивалентное сопротивление. Формулы (1.5) и (1.6) можно представить также в виде:

i_amax=SU_упр(1-cosq), … (1.5')

cosq = - 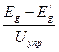, … (1.6')

где E_g^' = E_g0-DE_a - напряжение запирания, при котором угол отсечки q=90⁰, а U_упр носит название управляющего напряжения суммарного тока, с ним всегда совпадает по фазе первая гармоника суммарного тока, а в недонапряженном режиме, когда сеточным током можно пренебречь - первая гармоника анодного тока. (Методика определения статических параметров лампы S и D, напряжения сеточного приведения E_g0, а также напряжения запирания E'_g , изложена в Приложении 2).