При изучении непрерывных цепей было установлено, что описание таких цепей можно проводить при помощи временных и частотных характеристик. Аналогичные характеристики можно определить для линейных дискретных цепей.
Импульсная характеристика линейной дискретной цепи представляет собой отклик (реакцию) цепи на входной сигнал в виде единичного импульса (единичного отсчета) ![]()
![]() , (8.33)
, (8.33)
где единичный импульс характеризуется следующими параметрами
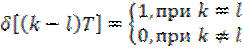 . (8.34)
. (8.34)
Так, например, импульсная характеристика цепи, описываемой уравнением
![]()
![]() , (8.35)
, (8.35)
определяется, если положить ![]()
![]() . (8.36)
. (8.36)
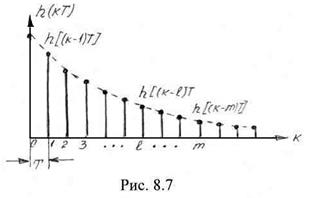
и представляет собой последовательность отсчетов, которые совпадают с коэффициентами ![]() . Действительно, в соответствии с (8.34) при
. Действительно, в соответствии с (8.34) при ![]()
![]() , при
, при ![]()
![]() и т.д. Иными словами для рассматриваемой цепи
и т.д. Иными словами для рассматриваемой цепи
![]() . (8.37)
. (8.37)
Тогда уравнение (8.35) с учетом (8.37) можно записать следующим образом
![]() . (8.38)
. (8.38)
 Из условия физической реализуемости цепи
Из условия физической реализуемости цепи
![]() , при
, при ![]() ,
,
что означает, что отклик не может появиться раньше входного сигнала верхний предел суммы (8.38) можно заменить на k и тогда
![]() . (8.39)
. (8.39)
Уравнение (8.39) представляет собой дискретный аналог интеграла Дюамеля. Таким образом, как и в непрерывной цепи, сигнал на выходе дискретной цепи представляет собой свертку входного сигнала и импульсной характеристики цепи. Однако, в отличие от интеграла Дюамеля свертка (8.39) называется дискретной.
Возвратимся к разностному уравнению (8.32) и представим его в виде:
![]()
![]() .. (8.40)
.. (8.40)
Применим к обеим частям этого уравнения преобразование Лапласа с учетом того, что
![]() .
.
Тогда уравнение (8.40) принимает вид
![]()
![]() .
.
Передаточная функция дискретной цепи
![]() . (8.41)
. (8.41)
Подставляя в это выражение ![]() , получим комплексный коэффициент передачи дискретной цепи
, получим комплексный коэффициент передачи дискретной цепи
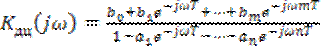 . (8.42)
. (8.42)
Очевидно, АЧХ и ФЧХ цепи определяется как модуль и аргумент выражения (8.42).
В качестве примера найдем комплексный коэффициент передачи цепи, описываемой уравнением (8.31). Приводя это уравнение к виду (8.40), после несложных преобразований получим
![]() .
.
Амплитудно-частотная характеристика цепи (рис. 8.8а)
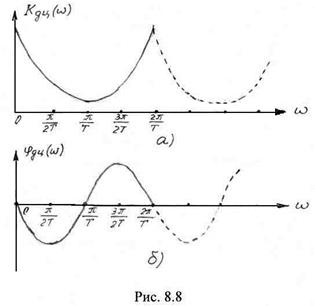
![]()
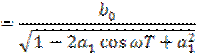
и фазо-частотная характеристика (рис. 8.8б)
![]()
![]() ,
,
имеют периодический характер, что свойственно для всех дискретных цепей.

