2.1. Формы представления информации

2.2. Классификация дискретных представлений

2.3. Рациональное представление информации

2.4. Точностные характеристики передаваемой информации

2.1. Формы представления информации

Наиболее характерными для современных РСПИ являются три формы представления сообщений, которые формируются на борту и передаются по линиям связи:

1. Сообщения о наличии/отсутствии некоторого априорно известного сообщения (включения/выключения двигателей, удары метеорита). В этом случае требуется определить момент времени, когда произошло событие. Параметры указанного типа называются сигнальными. Для фиксации события имеется несколько возможностей:

а) в момент совершения события посылается специальный сигнал;

б) в момент совершения события изменяется уровень напряжения, который подлежит измерению.

2. Сообщения о величинах характеризуют значения параметров в определенный момент времени. Контролируемые величины имеют различную физическую природу. Поэтому, для формирования сообщений используются первичные преобразователи. При нелинейности канала передачи необходимо произвести калибровку амплитуды и масштабирование по времени.

3. Сообщения о процессах должны с заданной точностью воспроизводить процессы на определенном отрезке времени, т.е. в этом случае также необходимо производить калибровку амплитуды и масштабирование по времени.

Существует два основных способа представления процессов: аналоговый и дискретный. Аналоговое представление заключается в том, что электрическая величина, играющая роль сообщения, формируется непрерывно. Такое представление используется в системах ЧРК, где непрерывное напряжение модулирует несущие или поднесущие гармонические колебания. Дискретное представление делится на дискретно-аналоговое и дискретно-квантованное (цифровое). Дискретно-аналоговое представление сводится к тому, что непрерывный процесс заменяется совокупностью аналоговых выборок, которые формируются через определенные интервалы времени (используются АИМ, ШИМ, ВИМ). Дискретно-квантованное представление отличается от дискретно-аналогового тем, что выборки формируются в цифровой форме.

2.2. Классификация дискретных представлений

Дискретно-аналоговые и цифровые представления могут быть классифицированы следующим образом (рисунок 2.1).

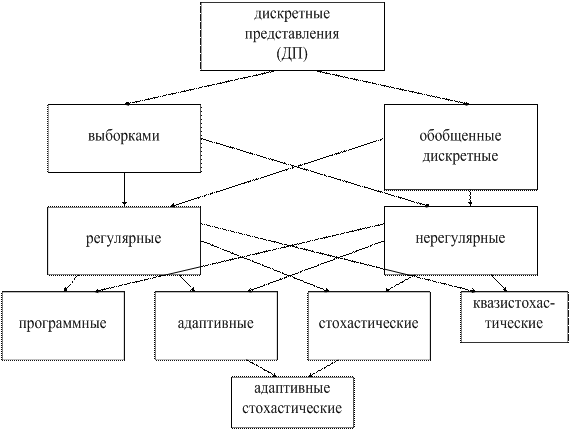
Рисунок 2.1

Дискретные представления – это процесс замены непрерывного сообщения x(t) (первичный сигнал) функцией дискретного времени . В общем случае дискретное представление может быть описано выражением:

Х1,Х2,…,Хn = АХ(t), (2.1)

где Х1…Хn – координаты сообщения; А – оператор представления.

При линейности оператора представления справедливо равенство:

, i = 1,2,...n , (2.2)

где Vi(t) – весовая функция ; Т – интервал представления.

Исходное сообщение восстанавливается с помощью оператора восстановления В по формуле:

, (2.3)

где Wi(t) – координатная (восстанавливающая, синтезирующая) функция, знак * указывает отличие восстановленного сообщения от исходного за счет искажений и шумов.

При представлении выборками весовые функции Vi(t)= δ(t – ti) , при этом Xi =X(ti).

При обобщенном дискретном представлении координаты сообщения представляют собой коэффициенты некоторого ряда, это позволяет сократить количество координат, т.е. объем выборки. В качестве координат функций могут использоваться полиномы Чебышева, Лежандра, Уолша и др.

При регулярных дискретных представлениях координаты X1, Xn формируются через одинаковые промежутки времени. Такие системы наиболее широко распространены благодаря простоте технической реализации.

Определим основные особенности классов дискретных представлений.

Программируемые дискретные представления предусматривают возможность изменения алгоритма представления, объема координат, показателя точности и других характеристик по определенной априори установленной программе.

Адаптивные дискретные представления дают возможность изменять те же характеристики автоматически на основе анализа данных об изменяемом сообщении и имеют цель приспособиться к этим изменениям.

Приведем классификацию адаптивных алгоритмов дискретизации (рисунок 2.2).

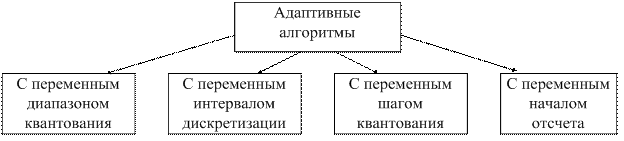
Рисунок 2.2

Адаптивные дискретные представления с переменным диапазоном квантования позволяют уменьшить объем сообщения при заданном показателе верности путем согласования динамического диапазона характеристики квантования и диапазона сигнала (например система адаптивной импульсно – кодовой модуляции).

Система с переменным интервалом дискретизации (например, система адаптивной дискретизации) используется, когда в процессе передачи изменяется полоса спектра частоты сообщения. Введение такой адаптации позволяет в несколько раз уменьшить среднюю частоту дискретизации.

Система с переменным шагом квантования (например, система адаптивной δ – модуляцией) позволяет уменьшить, по сравнению с равномерным квантованием, среднеквадратическую погрешность представления или уменьшить требуемую скорость передачи.

Система с переменным уровнем начала отсчета обычно использует разностные виды модуляции, например разностную импульсно – кодовую модуляцию. Формирование разностей значений выборок равноценно перемещению уровня начала отсчетов, что позволяет уменьшить число уровней квантования.

Стохастические дискретные представления предполагают преднамеренное введение элемента случайности в процесс преобразования сообщения для увеличения точности представления исходного процесса. В псевдослучайный шум добавляют сигнал перед квантованием, а на приемной стороне осуществляется подсчет квантованных значений двух соседних уровней в интересах увеличения точности представления.

При квазистохастических ДП используется комбинация детерминированного и случайного элемента в процессе формирования координат сообщения.

Адаптивные стохастические представления – результат соединения адаптивных и стохастических представлений, при которых одна группа характеристик изменяется стохастически, а другая адаптируется к измененному сообщению.

2.3. Рациональное представление информации

При ракетно–космических исследованиях наметилась постоянная тенденция к росту космических измерений и регистрации на борту летательного объекта информации. На ракете – носителе Сатурн – 5 системой измерения контролировалось около 2400 сигналов, а объем измерений в одном пуске достигал 6 млрд. двоичных слов. Для космического аппарата «Аполлон» этот объем возрос на порядок при количестве датчиков равном 20 тыс. Для космического объекта типа «Пионер – 10», предназначенного для проведения измерений в дальнем космосе, объем измерений равен двоичных слов. Эти обстоятельства обусловливают необходимость увеличения скорости передачи информации по радиоканалам.

Стоимость радиоканала передачи информации в настоящее время соизмерима, а иногда превышает стоимость бортовой системы. Однако по оценкам специалистов в связи со сложностью алгоритма вторичной обработки информации при анализе характеристик летательного и космического аппарата обычно используют 5-10% данных, полученных с борта. Для вычисления вероятностных характеристик наблюдаемых параметров бывает достаточно обработать 0,1-1% полученной информации. Т.о, эффективность бортовой системы измерений низка, несмотря на затраты значительных средств. В связи с этим системы телеизмерений на борту стали превращаться в бортовые системы сбора и обработки информации (БССО). Одна из первых систем БССО была разработана для ракет типа ТИТАН -3.

Эта БССО выполняла следующие задачи:

1. Адаптивный опрос и сжатие телеметрической информации.
2. Вычисление статистических характеристик наблюдаемых процессов.
3. Кодирование информации с контролем достоверности.
4. Определение летно-тактических характеристик бортовой системы.

Благодаря использованию ЭВМ стало возможно перенести на борт целиком или частично обработку измеряемых данных. Только таким путем, а не увеличивая пропускную способность канала передаваемой информации, можно решить задачу передачи возрастающего объема сведений. Дальнейший рост скорости передачи информации в УКВ и СВЧ диапазонах затруднен. Поэтому, начиная с 1965 года, начинают интенсивно изучаться различные методы рационального представления информации.

Основные направления исследований:

1. Согласование частот опросов с характеристиками сигнала в случае регулярных выборок и заданном способе восстановления сообщения.
2. Разработка эффективных обобщенно-дискретных представлений сообщений.
3. Разработка квазиобратимых методов сжатия данных.
4. Исследование методов эффективного кодирования.
5. Определение помехоустойчивых кодов и узкополосных методов модуляции.

Натурные испытания алгоритмов квазиобратного сжатия данных на ракете “Полярис” показали, что при точности восстановления данных 1% средний коэффициент сжатия составляет 12-30. Использование системы сжатия данных на космическом аппарате “Апполон” сократило затраты на 200 млн. $. Наибольшего эффекта в смысле сокращения избыточности следует ожидать от реализации методов необратимого сжатия, которые не позволяют восстановить на приемной стороне передаваемую реализацию как функцию времени.

2.4. Точностные характеристики передаваемой информации

Для характеристики точности передаваемой информации в РТМС применяют различные показатели верности. В соответствии с введенной выше классификацией необходимо получить оценки точности величины, функции и совокупность величин.

1. Величина (рисунок 2.3), где - текущая ошибка.

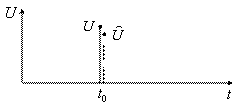
Рисунок 2.3

В качестве показателя верности используется: 1. Среднеквадратическое отклонение (СКО)

, (2.4)

где - операция усреднения, - среднее значение ошибки. 2. Среднеквадратическое значение (СКЗ)

. (2.5)

3. Относительная ошибка , где .

В ряде случаев бывает удобно приводить ошибки не к шкале , а к эффективному значению сигнала. Для эргодических процессов СКЗ сигнала совпадает с эффективным значением.

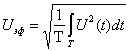. (2.6)

Тогда эффективная относительная ошибка равна: .

Обычно в РСПИ используется понятие отношения сигнал/шум, связанное с эффективной относительной ошибкой соотношением: .

2. Функция (рисунок 2.4), где - текущая ошибка.

Рисунок 2.4

В качестве показателей верности используются математически вводимые расстояния:

, (2.7)

. (2.8)

3. Совокупность величин (рисунок 2.5), где , , … , - текущая ошибка.

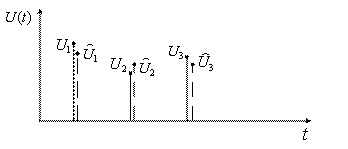
Рисунок 2.5

При оценке совокупности величин в качестве показателя вероятности используют:

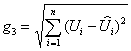(2.9)

(2.10)