До сих пор мы рассматривали модуляцию несущего колебания детерминированным процессом u(t), который отображает определенное сообщение или отдельную его реализацию. Совокупность же возможных сообщений представляет собой некоторый случайный процесс. Так, при передаче речи или музыки статистические свойства передаваемых сообщений очень близки к свойствам нормального случайного процесса. Важнейшими характеристиками колебания, модулированного случайным процессом, являются функция корреляции и энергетический спектр.

Следует подчеркнуть, что модулированный сигнал является нестационарным случайным процессом даже тогда, когда модулирующие процессы (сообщения) стационарны. Энергетический спектр нестационарного случайного процесса определяется посредством двукратного усреднения — по множеству и по времени. Сначала определяется усредненная по времени корреляционная функция, а затем обратным преобразованием Фурье — искомый энергетический спектр.

Рассмотрим случай, когда передаваемое сообщение u(t) представляет собой стационарный процесс с u(t)=0, а переносчик — гармоническое колебание .

При амплитудной модуляции

s(t) = А0[1 + ти(t)]cos ω0t,

где m — среднеквадратическое значение коэффициента модуляции. Функция корреляции модулированного сигнала

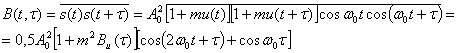
где Bu(t) — функция корреляции передаваемого сообщения u(t). Как видим, функция B(t, τ) зависит от времени, что указывает на нестационарность модулированного сигнала. После усреднения по времени получаем

(3.52)

Применяя к В (τ) преобразование Фурье (2.84), находим энергетический спектр сигнала при AM

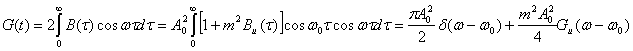
Таким образом, спектр модулированного по амплитуде гармонического колебания случайным процессом состоит из несущего колебания с частотой и смещенного на спектра передаваемого сообщения u(t).

Сигнал при угловой модуляции (ЧМ и ФМ) можно записать в общем виде

s(t) = А0cos ,

При ФМ , а при ЧМ.Здесь и — среднеквадратические значения девиации соответственно фазы и частоты.

Функция корреляции модулированного сигнала

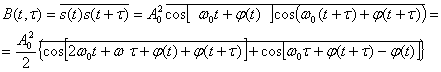
При усреднении по времени первое слагаемое обращается в нуль. Второе слагаемое не зависит от времени t поэтому

Обозначим разность и по известной формуле представим косинус суммы двух углов в виде

Средние по множеству значения косинуса и синуса можно найти, если известен закон распределения вероятностей сообщения u(t). Если u(t) подчиняется нормальному закону, то , являющееся линейным преобразованием от u(t), также будет иметь нормальное распределение с нулевым средним значением и дисперсией . Легко убедиться, что в этом случае:

Таким образом, усредненная по времени функция корреляции сигнала при угловой модуляции

(3.54)

Дисперсию процесса можно выразить через функцию корреляции или энергетический спектр сообщения u(t). Действительно.

(3.55)

где — функция корреляции процесса . При , поэтому ; при ЧМ , где , поэтому . Далее можно определить энергетический спектр модулированного сигнала путем преобразования Фурье (2.81) от функции (3.54).