Дифференциальное уравнение генератора

Обратимся вновь к схеме рис. 15.2. По первому закону Кирхгофа

или

Эти уравнения отличаются от соответствующих уравнений одиночного колебательного контура, полученных в 15.1. Физические процессы в автоколебательных цепях , тем, что в правой части записан коллекторный ток i_К.

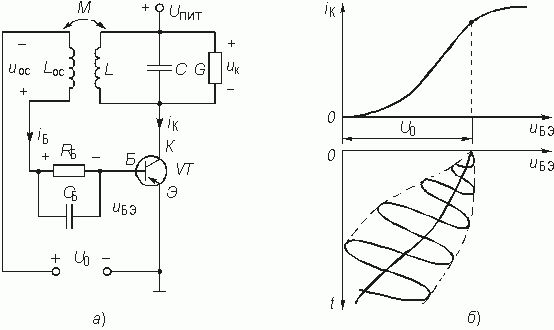
Вольт-амперная характеристика транзистора i_К = F(и_БЭ – U₀) в окрестности рабочей точки U₀ является, вообще говоря, нелинейной, так как ток коллектора i_К нелинейно зависит от напряжения и_БЭ – U₀. Из рис. 15.2 следует, что напряжение ОС, снимаемое с катушки индуктивности обратной связи L_ос, равно u_ос = и_БЭ – U₀, поэтому в дальнейшем удобно рассматривать ВАХ i_К = F(u_ос) = = i_К(u_ос).

Заметим далее, что напряжение ОС u_ос вычисляется через коэффициент взаимной индуктивности М и ток в катушке L

В свою очередь, ток в катушке i_Lи напряжение на ней u_к связаны соотношением u_к = Ldi_L/ dt, поэтому напряжение ОС u_ос можно выразить через напряжение на контуре u_к:

Вернемся к уравнению (15.4). Продифференцируем его по времени и разделим обе части на С:

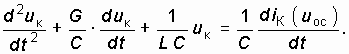
В отличие от уравнения (15.1) для одиночного колебательного контура в правой части уравнения (15.6) присутствует вынуждающая составляющая di_К(u_ос)/ dt. Производную функции i_К(u_ос) будем искать как производную сложной функции:

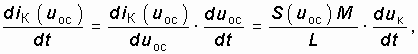
где S(u_ос) = di_К(u_ос)/ du_ос – дифференциальная крутизна ВАХ транзистора, нелинейно зависящая от напряжения u_ос.

При дифференцировании напряжения u_ос по времени учтено соотношение (15.5).

Подставив (15.7) в (15.6), получим дифференциальное уравнение автогенератора

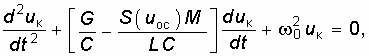
где – резонансная частота контура.

Это дифференциальное уравнение является нелинейным, так как коэффициент при первой производной напряжения u_к, в который входит крутизна S(u_ос), нелинейно зависит от напряжения обратной связи u_ос (или, что то же, от искомой переменной – напряжения на контуре). Уравнение (15.8) определяет все свойства автогенератора и позволяет установить условия самовозбуждения колебаний, особенности стационарного режима и характер переходных процессов в автогенераторе.

Условие возникновения колебаний

При определении условий самовозбуждения следует учесть, что амплитуда нарастающих колебаний в автогенераторе достаточно мала и работа автогенератора происходит на линейном участке ВАХ транзистора i_К = F(u_ос). Иными словами, для малых амплитуд колебаний ВАХ можно аппроксимировать линейно-ломаной функцией, крутизна которой в рабочем диапазоне амплитуд напряжения является постоянной, не зависящей от напряжения u_ос, т. е. S(u_ос) = S. В этом случае дифференциальное уравнение автогенератора (15.8) становится линейным:

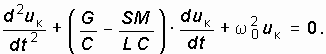
Перепишем его в виде

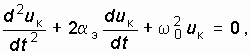
где – эквивалентный коэффициент затухания колебательного контура, включенного в цепь коллектора транзистора.

Сопоставление уравнения (15.9) с уравнением (15.2) для одиночного колебательного контура показывает, что при включении колебательного контура в коллекторную цепь транзистора коэффициент затухания контура a _э уменьшится на величину SM/ 2LC, зависящую от взаимоиндукции М, т. е. от ОС:

где a = G/ 2С – коэффициент затухания свободных колебаний контура.

Чтобы в контуре возникли нарастающие по амплитуде колебания, необходимо сделать коэффициент a _э < 0. Это возможно при условии SM/ LС > G/ C. Отсюда получаем значение коэффициента взаимной индукции М при котором в колебательном контуре возникнут нарастающие по амплитуде колебания:

Условие (15.10) называется условием самовозбуждения LC-автогенератора. Величина M_кр = LG/ S называется критическим коэффициентом взаимной индукции. Колебания в автогенераторе могут возникнуть только при обратной связи с М > M_кр. При М < M_кр коэффициент затухания контура a _э > 0 и колебание в контуре становится затухающим. Коэффициент a _э в (15.9) можно представить в следующем виде:

где G_вн = —(SM/ L) – проводимость, вносимая в контур за счет действия обратной связи. Знак коэффициента М может меняться в зависимости от направления включения (согласно или встречно) вторичной обмотки трансформатора. При М > 0 вносимая проводимость оказывается отрицательной и если ее величина |G_вн| > G, что имеет место при М > M_кр, то a _э < 0 и в контуре возникнут нарастающие по амплитуде колебания. Положительные значения М соответствуют положительной ОС, отрицательные – отрицательной ОС.

Эквивалентная схема колебательного контура, соответствующая уравнению (15.9) с a _э из (15.11), приведена на рис. 15.4. Отрицательная общая проводимость контура G + G_вн < 0 при М > M_кр свидетельствует о том, что в контур поступает энергии больше, чем расходуется ее на активной проводимости контура G.

Стационарный режим работы

При больших амплитудах сигнала нелинейностью ВАХ транзистора i_К = F(u_ос) пренебречь уже нельзя: в общем случае она должна аппроксимироваться степенным полиномом высокого порядка.

Ток в цепи коллектора в стационарном режиме будет из-за нелинейности ВАХ несинусоидальной периодической функцией времени и может быть представлен рядом Фурье

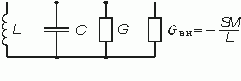
Падение напряжения u_к на колебательном контуре, настроенном на частоту w ₀, определяется в основном первой гармоникой коллекторного тока, так как сопротивление контура для тока этой гармоники является наибольшим (равным R_оэ = l/ G), а для остальных гармоник – достаточно малым. Напряжение ОС u_ос, определяемое (15.5), вследствие этого также будет гармоническим; его можно записать в виде

Введем понятие средней крутизны ВАХ

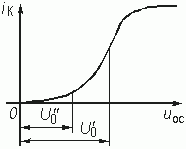
Она определяется отношением амплитуды I_m1 первой гармоники тока i_К, протекающего через нелинейный элемент, к амплитуде U_mос, действующего на нелинейный элемент напряжения u_ос. Среднюю крутизну часто поэтому называют крутизной ВАХ по первой гармонике. Средняя крутизна S_cp(U_mос) зависит от амплитуды напряжения обратной связи U_mос и от положения рабочей точки U₀. На рис. 15.5 показана типичная ВАХ транзистора i_К = = F(u_ос). Пусть рабочая точка выбрана на середине линейного участка характеристики (U₀ = U_0¢ ). При увеличении амплитуды напряжения U_mос средняя крутизна, пока мы находимся в пределах линейного участка характеристики, остается неизменной. Затем средняя крутизна ВАХ падает (рис. 15.6, а). Если выбрать рабочую точку (U₀ = U_{0¢ ¢} )на нижнем загибе характеристики i_К = = F(u_ос), где средняя крутизна мала, то по мере увеличения амплитуды U_mос будут охватываться участки характеристики с большей крутизной и, следовательно, S_cp(U_mос) станет расти. После прохождения участка с наибольшей крутизной дальнейшее увеличение U_mос приводит к уменьшению средней крутизны (рис. 15.6, б).

Дифференциальное уравнение (15.8) при работе генератора в режиме больших амплитуд является, вообще говоря, нелинейным, поскольку в коэффициент при du_к/ dt входит средняя крутизна S_cp(U_mос), зависящая от амплитуды U_mос напряжения ОС.

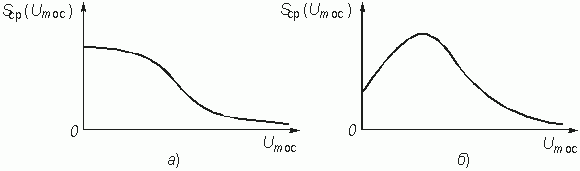
Однако в стационарном режиме, когда гармоническое напряжение на контуре u_к характеризуется установившейся (стационарной) амплитудой U_mк, гармоническое напряжение обратной связи u_ос также описывается установившейся (стационарной) амплитудой U_mос. При этом средняя крутизна S_cp(U_mос) является постоянной величиной и дифференциальное уравнение (15.8) можно считать линейным:

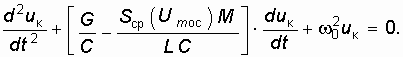
В стационарном режиме генерируются незатухающие гармонические колебания. Это имеет место, когда

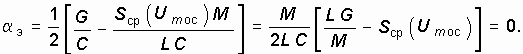
Отсюда установившееся (стационарное) значение средней крутизны равно

С учетом этого обозначения коэффициент затухания контура перепишем в виде

Из формулы (15.13) при a _э = 0 можно определить стационарную амплитуду , которая соответствует точке пересечения кривой S_ср(U_mос) и прямой линии . Рис. 15.7 иллюстрирует процесс нахождения стационарной амплитуды для двух зависимостей средней крутизны, соответствующих различным положениям рабочей точки на ВАХ (см. рис. 15.5).

Частота генерируемых колебаний, определяемая как w _г = = , в стационарном режиме при a _э = 0 совпадает с резонансной частотой колебательного контура w ₀.

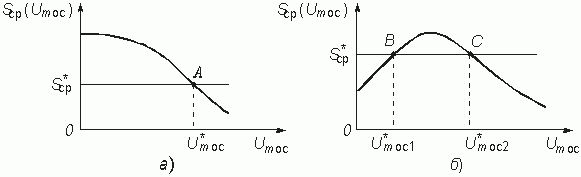
Устойчивость стационарного режима

Стационарный режим называется устойчивым, если отклонение D U_m.. от стационарной амплитуды с течением времени будет уменьшаться.

Рассмотрим стационарный режим в точке А на рис. 15.7, а. Отклонение —D U_m.. от амплитуды приведет к S_ср(U_m..) > и, в соответствии с (15.13), к a _э < 0, т. е. амплитуда колебаний будет увеличиваться и приближаться к стационарному значению. При отклонении +D U_m.. средняя крутизна S_ср(U_m..) < , т. е. коэффициент затухания a _э, станет положительным и амплитуда уменьшится, вновь приближаясь к стационарной. Таким образом, точка А соответствует устойчивому стационарному режиму.

Точка В на рис. 15.7, б соответствует неустойчивому режиму, так как отклонение амплитуды U_m.. от стационарного значения в сторону уменьшения ведет к S_ср(U_m..) < и a _э > 0, т. е. к дальнейшему уменьшению амплитуды U_m.., а отклонение амплитуды U_m.. от стационарной в сторону увеличения вызовет дальнейший ее рост и переход в следующее стационарное состояние, отмеченное точкой С.

Стационарное состояние в точке С является устойчивым, в чем легко убедиться с помощью рассуждений, аналогичных приведенным выше.

Можно заметить, что справедливо следующее утверждение: пересечение прямой линии с кривой средней крутизны S_ср(U_m..) дает устойчивые значения стационарной амплитуды , если на этом участке dS_ср(U_m..)/ dU_m.. < 0 и неустойчивые значения – если dS_ср(U_m..)/ dU_m.. > 0. Поэтому условие dS_ср(U_m..)/ dU_m.. < < 0 можно считать условием устойчивости стационарного режима.

Режим самовозбуждения

Будем менять коэффициент взаимной индукции М и наблюдать за процессом возникновения колебаний. Этот процесс зависит также от выбора рабочей точки на ВАХ (напряжения смещения U₀).

Выбору рабочей точки в области наибольшей крутизны (напряжение смещения U_0¢ на рис. 15.5) соответствует график средней крутизны S_ср(U_m..), показанной на рис. 15.8, а.

При изменении параметра М меняется значение средней крутизны = LG/ M. На рис. 15.8, а изображены несколько прямых , соответствующих различным М.

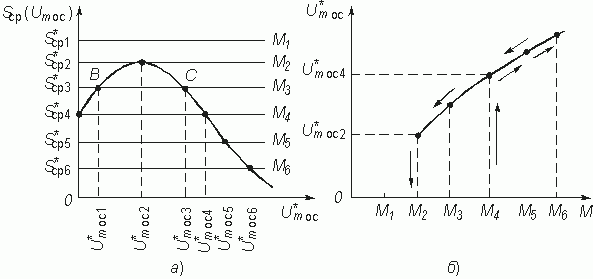
При М = М₁ колебания в автогенераторе возникнуть не могут, поскольку > S_ср(U_m..) и коэффициент затухания контура a _э > 0, значит, любые случайные флуктуации напряжения U_m.. будут быстро затухать.

Увеличение М до значения М₂ приводит к = S_ср(U_m..) и a _э = 0. Дальнейший рост М снижает значение ; при этом коэффициент a _э становится отрицательным, т. е. a _э < 0. Таким образом, начиная с M М₂, в автогенераторе возникают незатухающие колебания с соответствующими стационарными амплитудами . С увеличением М стационарная амплитуда колебаний плавно нарастает. Уменьшение М вызовет плавное уменьшение значений стационарной амплитуды . График зависимости стационарной амплитуды генерируемых в автогенераторе колебаний от коэффициента взаимной индукции М приведен на рис. 15.8, б. Такой режим самовозбуждения генератора, при котором амплитуда колебаний плавно нарастает с увеличением М, называется мягким режимом самовозбуждения.

Если рабочую точку выбрать на нижнем загибе ВАХ, как это показано на рис. 15.5 при U₀ = U_{0¢ ¢} , то график средней крутизны S_ср(U_m..) имеет вид, показанный на рисунке 15.9, а.

При М, равном М₁, М₂ и М₃, наличие малых флуктуаций напряжения U_m.. не приведет к установлению стационарной амплитуды, поскольку при значениях , равных , и ,коэффициент затухания контура a _э будет положительным.

Только начиная с М = М₄, когда S_ср(U_m..) = и a _э = 0, малые флуктуации амплитуды напряжения обратной связи начинают быстро расти, пока не установится устойчивое стационарное значение амплитуды . Дальнейшее увеличение М ведет к плавному росту стационарной амплитуды.

При плавном уменьшении обратной связи (коэффициента М) стационарная амплитуда будет также плавно уменьшаться. Колебания сорвутся при значении М = М₂, меньшем М₄, когда перестанет выполняться условие стационарности S_ср(U_m..) = . На рис. 15.9, б дан график изменения амплитуды в зависимости от М. Такой режим, когда колебания возбуждаются при большем значении М, а срываются при меньшем значении М, называется жестким режимом самовозбуждения.

Достоинством мягкого режима самовозбуждения является плавное изменение амплитуды при изменении коэффициента М; достоинством жесткого режима является высокий КПД за счет работы с отсечкой коллекторного тока.

Можно объединить достоинства мягкого и жесткого режимов самовозбуждения, если ввести в автогенератор цепь автоматического смещения R_Б С_Б (рис. 15.10, а). Исходное смещение U₀ выбирают таким, при котором рабочая точка находится на участке наибольшей крутизны ВАХ, что соответствует мягкому режиму. При нарастании амплитуды колебаний u_ос в цепи базы за счет нелинейности ВАХ i_Б = F(u_БЭ) произойдет детектирование колебаний. Возрастание постоянной составляющей тока базы I_БO, которая на резистивном сопротивлении R_Б создает напряжение I_БO× R_Б, приводит к уменьшению результирующего напряжения смещения U₀ – I_БO× R_Б и, как результат, к сдвигу рабочей точки влево (рис. 15.10, б) к нижнему загибу ВАХ i_К = F(u_БЭ).

Переходный процесс заканчивается (при соответствующем значении R_Б) установлением жесткого стационарного режима с более высоким КПД.