Флуктуационная помеха представляет собой стационарный процесс с нормальным распределением вероятностей (гауссов процесс). Это непосредственно следует из центральной предельной теоремы теории вероятностей, согласно которой распределение суммы большого числа независимых случайных величин сходится к нормальному закону. Флуктуационная помеха, представляющая собой сумму большого числа независимых колебаний, удовлетворяет условиям этой теоремы.

Одномерная плотность вероятности гауссова процесса определяется следующим выражением:

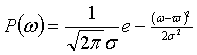(2.27)

где — среднее значение процесса, σ² — его дисперсия. Для флуктуационной помехи положительные и отрицательные значения ω встречаются одинаково часто и поэтому = 0. Дисперсия в этом случае равна средней мощности помех Р, а эффективное значение помехи UПЭ= Таким образом, плотность вероятности помехи приводится к виду

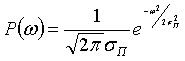(2.28)

Соответственно интегральная функция распределения

(2.29)

где u=ω/σ— относительное значение помехи:

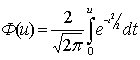(2.30)

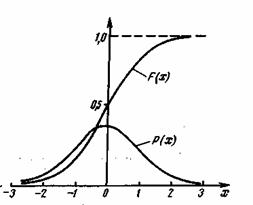
Рис. 2.4. Графики дифференциального и интегрального распределений гауссова процесса

Функция Ф(и) называется интегралом .вероятности или функцией Крампа. Значения этой функции приводятся в таблицах (см. приложение 1). Заметим, что функция Ф(и) является нечетной: Ф(-и)=-Ф(и), кроме этого, Ф()=1 и Ф(0)=0. На рис. 2.4 изображены графики дифференциального и интегрального распределений гауссова процесса.

Зная закон распределения вероятностей, легко найти вероятность того, что уровень помехи примет значение, лежащее в заданных пределах, например, между и . Очевидно,

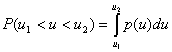
Подставляя р(и) согласно (2.28), находим

(2.31)

Вероятность того, что помеха превысит некоторый пороговый уровень и0, можно определить непосредственно из (2.31), если в последнем положить и :

(2.32)

Расчеты на основании (2.32) показывают, что вероятность превышения помехой порогового уровня быстро падает с увеличением . Так вероятность превышения уровня =1 равна 0,16, при 3 эта вероятность уже равна 0,0013, а при =4 она равна 3,5 и т. д. Отсюда следует, что колебания помехи практически не превышают трехкратного эффективного значения :помехи. Пикфактор помехи, определяемый как отношение максимального значения к эффективному, обычно лежит в пределах 3,5÷4,6. Поэтому флуктуационную помеху часто называют гладкой, в отличие от импульсных помех, для которых это отношение обычно много больше.

Двумерное распределение флуктуационной помехи имеет следующее выражение:

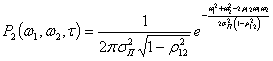(2.33)

Если помеха представлена последовательностью своих значений ωk=ω(tk) (k=1,2...), то ее исчерпывающим описанием будет n-мерное распределение

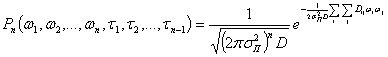(2.34)

где D — определитель п-го порядка корреляционной матрицы, а

— алгебраическое дополнение элемента . Здесь = коэффициент корреляции.

Из (2.34) следует, что гауссова функция распределения любого порядка содержит в качестве параметров только средние значения и моменты второго порядка (функцию корреляции), для нахождения которых достаточно знать лишь двумерную плотность вероятности, а тем самым и. Таким образом, нормальный случайный процесс вполне определяется заданием двумерной плотности вероятности.

Флуктуационная помеха называется белым шумом, если ее значения статистически независимы. В этом случае поэтому D=1, a

Следовательно, для белого шума n-мерный закон распределения согласно (2.34) будет

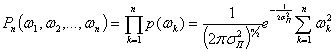(2.35)

Энергетический спектр такой помехи является равномерным (см. § 2.6). Следует иметь в виду, что понятие о белом шуме является идеализацией, так как энергетический спектр реальных процессов всегда убывает с частотой, а интервал корреляции имеет конечное значение Δτ0. Эта идеализация применима в тех случаях, когда интервал корреляции помехи много меньше постоянной времени системы, на которую она воздействует, или, иначе, когда в пределах полосы пропускания системы спектральную плотность помехи можно приближенно считать постоянной. В реальных системах эти условия обычно выполняются и помеху можно в первом приближении считать белым шумом.

Флуктуационный случайный процесс называется узкополосным, когда ширина спектра процесса относительно мала по сравнению со средней частотой этого спектра. Такого рода процессы имеют место на выходе схем, работающих на высоких и промежуточных частотах. Если смотреть на реализацию узкополосного процесса на экране осциллографа, то она будет иметь вид синусоиды с медленно меняющимися амплитудой (огибающей) и фазой. Мгновенные напряжения изменяются при этом со средней частотой спектра, а скорость изменения амплитуды определяется шириной спектра процесса. Процесс на выходе узкополосной системы внешне напоминает амплитудно-модулированное колебание со случайно изменяющимися огибающей и фазой. Аналитически узкополосный процесс можно представить в виде

(2.36)

где — средняя частота, U(t) и φ(t) — огибающая и фаза процесса — обе функции времени, медленно меняющиеся по сравнению с колебаниями на частоте .

Путем простого тригонометрического разложения (2.36) узкополосный процесс можно представить в виде суммы двух составляющих:

(2.37)

Здесь

U1(t) = U(t)cosφ(t) (2.38)

U(t) = U(t)sinφ(t) (2.39)

также являются медленно меняющимися функциями времени. Очевидно,

(2.40)

(2.41)

Если процесс (2.36) является гауссовым, то и его составляющие и будут иметь нормальное распределение с нулевым средним и дисперсией . В силу независимости составляющих и совместная плотность вероятности для одного и того же момента времени будет равна произведению одномерных плотностей вероятности и т. е.

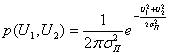(2.42)

Далее можно показать, что плотность вероятностей огибающей U узкополосного гауссова процесса определяется следующим выражением [6]:

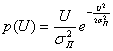
(2.43)

При расчетах вместо огибающей U удобно пользоваться ее нормированным значением z=U/.Подставив это значение в (2.43) и учитывая, что dz=, получим (2.44)

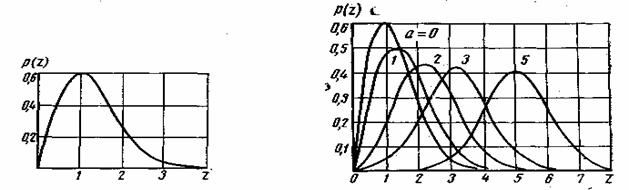
Рис. 2.5. Распределение Рэлея Рис. 2.6. Обобщенное распределение Рэлея

Это распределение известно под названием распределения Рэлея; его график изображен на рис. 2.5. Не следует путать распределение огибающей узкополосного нормального шума с распределением нормального широкополосного шума. В первом случае имеет место одностороннее, расположенное в положительной области, распределение Рэлея (рис. 2.5), а во втором — симметричное нормальное распределение (рис. 2.4).

Плотность вероятности фазы φ узкополосного гауссова процесса равномерна по всей области возможных значений φ :

(2.45)

В дальнейшем нам потребуются распределения вероятностей огибающей и фазы суммарного колебания гармонического сигнала s(t)=Acos и помехи ω(t). Если помеха представляет собой узкополосный гауссов шум, то согласно (2.37) суммарное колебание x(t) можно записать в виде

х(t)=s(t)+ω(t)= где

(2.46)

(2.47)

Плотность вероятности огибающей суммарного колебания сигнала и помехи в этом случае определяется следующим выражением:

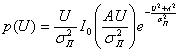(2.48)

где — модифицированная функция Бесселя нулевого порядка, — дисперсия помехи.

Распределение (2.48) называется обобщенным распределением Рэлея или распределением Раиса. При А=0 распределение (2.48) превращается в обычное распределение Рэлея (2.43).

Полагая и а=А/распределение Раиса можно записать в следующем виде:

(2.49)

На рис. 2.6. изображены графики этого распределения для различных значений где — мощность сигнала, — мощность помехи.

Выражение для плотности вероятности фазы суммарного колебания имеет следующий вид:

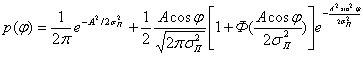(2.50)

где Ф(х) — функция Крампа (2.30).