Физиологические основы цветового зрения базируются на теории трехкомпонентного зрения, выдвинутой впервые М.В. Ломоносовым в 1756 г. Согласно этой теории мы допускаем существование на сетчатке глаза трех видов нервных аппаратов, каждый из которых обладает преимущественной чувствительностью к определенному участку видимого спектра – коротковолновому (синему), средневолновому (зеленому), длинноволновому (красному).
Изолированное возбуждение одного из этих аппаратов дает ощущение одного из трех насыщенных цветов — синего, зеленого, красного. Обычно (при наблюдении малонасыщенных цветов) воздействующее излучение содержит весь спектр видимого диапазона волн, но с разной спектральной интенсивностью. Это приводит к раздражению не одного, а двух или трех световоспринимающих аппаратов одновременно. При этом волны различной длины возбуждают эти аппараты в различной степени. Различное соотношение возбуждений световоспринимающих аппаратов вызывает ощущение цвета. Таким образом, анализ воздействующего излучения тремя селективными светочувствительными аппаратами глаза и последующий синтез результатов их возбуждений корой головного мозга вызывает ощущение большого числа цветовых оттенков окружающих нас предметов. Теория эта хорошо согласуется с законами смешения цветов, которые косвенно ее подтверждают.
В телевидении используется локальное, пространственное и бинокулярное смешение цветов. Локальное смешение может быть одновременным (оптическим), когда на одну поверхность проецируются два или несколько излучений, вызывающие каждый в отдельности ощущение разных цветов, и последовательным, когда аналогичные излучения воздействуют на глаз последовательно одно за другим. При быстрой смене излучений в зрительном аппарате возникает ощущение единого результирующего цвета. При пространственном смешении участки, окрашиваемые смешиваемыми цветами, имеют достаточно малые размеры и глаз воспринимает их как единое целое. Примером этому могут служить мелкие штрихи, мозаика и др. Воспроизведение цветного изображения на телевизионном экране в большинстве случаев основано на пространственном смешении цветов. Бинокулярным смешением называется смешение двух или нескольких цветов путем раздельного раздражения левого и правого глаза разными цветами, в результате чего возникает ощущение нового цвета.
В основном законе смешения утверждается, что любые четыре цвета находятся в линейной зависимости. Иначе говоря, любой цвет может быть выражен через любые три взаимно-независимых цвета:
f'F = r'R + g'G + b'B ; (2.1)
здесь f'F – излучение произвольного состава, единица которого обозначена через F, а количество единиц – через f'; R, G, В – единичные количества основных цветов; r', g', b' – множители, указывающие количества излучений, соответствующих цветам R, G, В, – или модули этих цветов.
Основными цветами называются взаимно-независимые цвета, которые нельзя получить смешением двух других, т.е. они не могут быть связаны уравнениями типа
r'R = g'G + b'B; g'G = r'R + b'B; b'B = r'R + g'G,(2.2)
Примером взаимно-независимых цветов являются красный (R), зеленый (G) и синий (В) .
Экспериментальную проверку законов смешения цветов удобно производить путем установления тождества цветов полей сравнения с помощью устройства, состоящего из гипсовой призмы, на одну из граней которой проецируется излучение исследуемого источника, а на другую грань – излучение от трех источников: красного R, зеленого G и синего В. Зрительная труба, при помощи которой ведутся наблюдения, направлена на ребро призмы, разделяющее освещенные грани. Следовательно, поле зрения трубы разделено на два поля сравнения: одно, освещаемое исследуемым цветом, другое – освещаемое смесью трех источников. Между каждым из трех источников R, G, В и призмой стоит устройство, ослабляющее полное излучение данного источника в определенное число раз. Меняя интенсивность потоков излучения, подаваемого на грань призмы от того или иного источника, колориметрист добивается уравнивания цвета (т.е. цветности и яркости) полей сравнения.
Необходимо отметить, что для чистых спектральных цветов нельзя получить цветового равенства (2.1) ни при каких значениях основных цветов R, G, В. Согласование для этих цветов наступает лишь тогда, когда один из основных цветов переносится на сторону исследуемого цвета.
В случае переноса в сторону исследуемого цвета, например красной составляющей, цветовое уравнение принимает следующий вид:
f'F + r'R = g'G + b'B ; (2.3)
или
f'F = – r'R + g'G + b'B ; (2.4)
Таким образом, при описании некоторых цветов с помощью уравнения (2.1) коэффициенты r', g', b' могут иметь отрицательные значения. Это позволяет расширить применимость форм цветового уравнения (2.1), показывающего, что в общем случае цвет определяется тремя независимыми переменными r',g',b', что подтверждает его трехмерность.
Знание численных значений цветовых коэффициентов r', g', b' полностью определяет воздействующее на глаз излучение и количественно, и качественно. Для определения только качественной характеристики светового потока цветности F достаточно знать не абсолютные, а относительные количества основных цветов r, g, b, определяемые из выражений
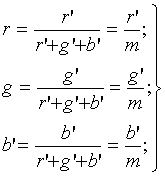 (2.5)
(2.5)
где m = r' + g' + b' — цветовой модуль.
Очевидно,что
r+g+b=1 (2.6)
Символы r, g, b носят название координат цветности.
В уравнении (2.1) множитель указывает f' – количество цвета F, необходимое для обеспечения цветового равенства. Известно, что яркость смеси равна сумме яркостей смешиваемых цветов, т.е.
f' = r' + g' + b' = m . (2.7)
Тогда, разделив (2.1) на цветовой модуль, получим
F = rR + gG + bB. (2.8)
Цвет F носит название единичного цвета; сумма его координат равна единице.
Координаты цветности являются зависимыми величинами, так как, зная две из них, третью находим из равенства (2.6). Это подтверждает двумерность параметра цвета – цветности и позволяет отобразить ее точкой в плоскости треугольника основных цветов.

