Шум квантования на выходе цифровой цепи не зависит от уровня сигнала. Чем выше уровень сигнала в цепи, тем лучше соотношение сигнал/шум. Но высокие уровни сигнала могут привести к переполнению (перегрузке) сумматора, т.е. к выходу числа за пределы разрядной сетки слева.
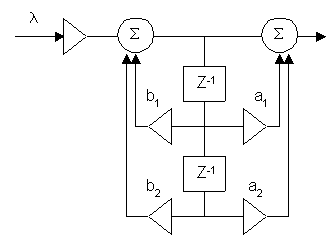
Чтобы получить нужный уровень применяется масштабирование сигнала. С этой целью на входе цепи устанавливают умножитель с коэффициентом умножения λ.
Для расчета λ используют различные методы.
1. Расчет λ по условию ограничения максимума сигнала.
Сигнал на выходе i-го сумматора, т.е. yi (n) можно рассчитать применением свертки:
Условия maxсигнала yi(n)
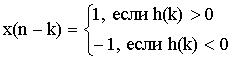
Учитывая эти условия получим формулу для максимально возможного сигнала на выходе сумматора.
Потребуем, чтобы maxyi(n) = 1
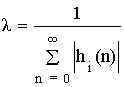
Расчет λ выполняется по каждому сумматору. Из всех λ выбирается наименьшее и округляется в меньшую сторону до ближайшего числа кратного степени 2, что позволяет осуществить умножение простым сдвигом числа в числовом регистре.
Расчет λ по условию max сигнала приводит к низким уровням сигнала цепи, поэтому расчет λ часто выполняется по условию ограничения энергии сигнала.
2. Расчет λ по условию ограничения энергии сигнала.
Расчет энергии сигнала на выходе i-го сумматора определяется:
формула справедлива для случайного
сигнала с равномерным энергетическим спектром, что соответствует реальному сигналу.
Энергия сигнала на выходе i-го сумматора равна энергии сигнала на входе, т.е. Wyi = Wx. В результате исходная формула примет вид:
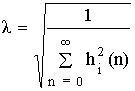
Уровень сигнала цепи получается выше, но здесь не исключена возможность перегрузки сумматора (но вероятность перегрузки мала).
3. Расчет λ по условию ограничения максимума усиления цепи.
Спектр сигнала на выходе i-го сумматора определяется:
Если ω∞ – частота максимального усиления сигнала, то условие максимума усиления сигнала запишется:
где: ω∞ – частота высокодобротного полюса
– коэффициенты высокодобротного полюса.
Потребуем, чтобы Y(ω∞) = X(ω∞), тогда выражение для максимального спектра выходного сигнала принимает вид:
1 = λ H(ω∞)
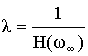
Расчет λ приводит к значениям λ, где–то между случаями 1 и 2. Расчет λ в этом случае применяется для каскадной реализации, когда масштабирование осуществляется внутри каждого звена, за счет чего масштабирование получается очень эффективным.