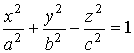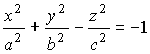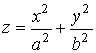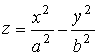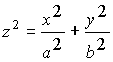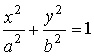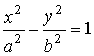3.3. Поверхности второго порядка
3.1. Линейные образы
3.1.1. Прямая на плоскости
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение прямой на плоскости | n=(A,B) - нормальный вектор прямой;
k - a - отрезок, отсекаемый прямой на оси х; b - отрезок, отсекаемый прямой на оси y; q=(l,m) - направляющий вектор прямой |
|
| уравнение прямой, проходящей через данную точку | ||
| уравнение прямой с данным угловым коэффициентом | ||
| уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | ||
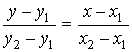 |
уравнение прямой, проходящей через две точки | |
| уравнение прямой в отрезках | ||
| каноническое уравнение прямой |
Формулы для вычисления угла между двумя прямыми на плоскости:
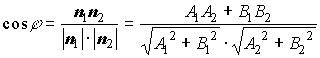 ;
; 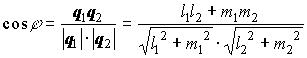 ,
,
где ![]() и
и ![]() -нормальный и направляющий векторы первой прямой;
-нормальный и направляющий векторы первой прямой;
![]() и
и ![]() - нормальный и направляющий векторы второй прямой.
- нормальный и направляющий векторы второй прямой.
Условия параллельности двух прямых на плоскости:
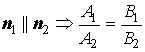 ;
;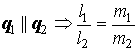 ;
;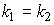 , где
, где 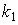 и
и 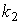 - угловые коэффициенты прямых.
- угловые коэффициенты прямых.
Условия перпендикулярности двух прямых на плоскости:
- n1
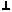 n2
n2 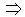 n1
n1 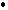 n2=0 или A1A2+B1B2=0;
n2=0 или A1A2+B1B2=0; - q1
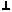 q2
q2 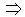 q1
q1  q2=0 или l1l2+m1m2=0;
q2=0 или l1l2+m1m2=0; 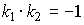
3.1.2. Плоскость в пространстве
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение плоскости в пространстве |
a,b,c – отрезки, отсекаемые плоскостью
p - длина перпендикуляра, опущенного |
|
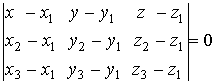 |
уравнение плоскости, проходящей через три точки |
|
| уравнение плоскости в отрезках | ||
|
нормальное уравнение плоскости |
Выражение направляющих косинусов через координаты нормального вектора:
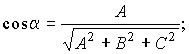
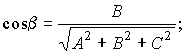
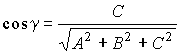 .
.
Формулы для вычисления угла между двумя плоскостями:
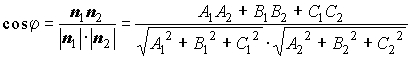 ;
;
где![]() и
и ![]() -нормальные векторы плоскостей.
-нормальные векторы плоскостей.
Условие параллельности двух плоскостей:
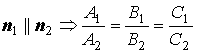 .
.
Условие перпендикулярности двух плоскостей:
n1![]() n2
n2 ![]() n1
n1![]() n2=0 или A1A2+B1B2+С1С2=0.
n2=0 или A1A2+B1B2+С1С2=0.
3.1.3. Прямая в пространстве
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
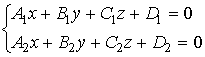 |
общие уравнения прямой в пространстве | направляющий вектор прямой; координаты фиксированных точек на прямой |
| канонические уравнения прямой в пространстве | ||
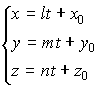 |
параметрические уравнения прямой в пространстве | |
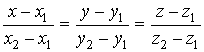 |
уравнения прямой, проходящей через две фиксированные точки |
Формулы для вычисления угла между двумя прямыми в пространстве:
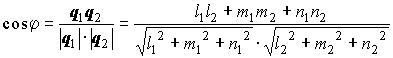 ,
,
где ![]() и
и ![]() - направляющие векторы прямых.
- направляющие векторы прямых.
Условие параллельности двух прямых в пространстве:
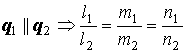 .
.
Условие ортогональности двух прямых в пространстве:
q1 ![]() q2
q2 ![]() q1
q1 ![]() q2=0 или l1l2+m1m2+n1n2=0.
q2=0 или l1l2+m1m2+n1n2=0.
3.2. Кривые второго порядка
Общее уравнение кривой второго порядка:
![]() .
.
3.2.1. Окружность
| Каноническое уравнение:
Радиус окружности: a. |
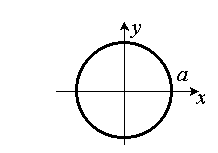 |
||||
| Параметрическое уравнение: | 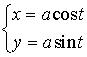 |
Уравнение в полярных координатах: | |||
| Уравнение окружности радиуса |
|||||
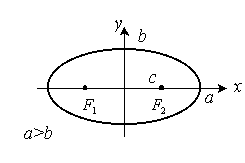
3.2.2. Эллипс
|
Каноническое уравнение:
Полуоси эллипса: |
 |
|||
|
Эксцентриситет: |
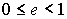 . . |
Параметрическое уравнение: | 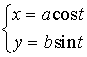 . . |
|
3.2.3. Гипербола
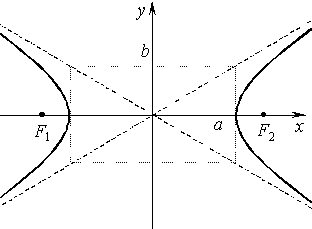
| Каноническое уравнение:
Действительная полуось: a, мнимая полуось: |
 |
|
|
Эксцентриситет: |
Асимптоты: |
Параметрическое |
3.2.4. Парабола
| Каноническое уравнение:
Параметр: p. |
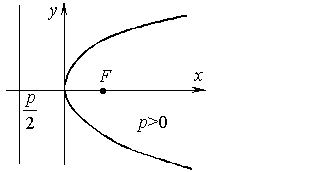 |
3.3. Поверхности второго порядка
|
Каноническое уравнение |
Наименование |
Параметры |
Чертеж |
|
|
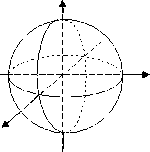
сфера |
a – |
 |
|
|
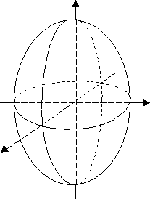
эллипсоид |
|
 |
|
|
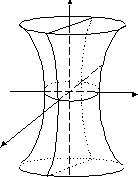
однополостный гиперболоид |
|
 |
|
|
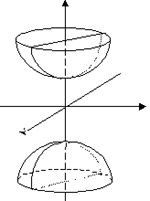
двуполостный гиперболоид |
|
 |
|
|
эллиптический параболоид |
|
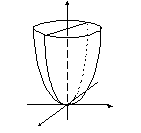 |
|
|
гиперболический параболоид |
|
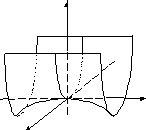 |
|
|
конус |
|
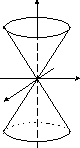 |
|
|
параболический цилиндр |
р - параметр |
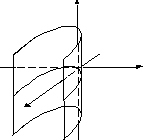 |
|
|
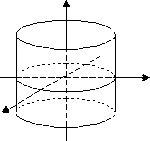
эллиптический цилиндр |
|
 |
|
|
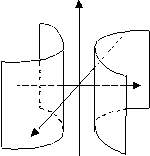
гиперболический цилиндр |
|
 |
3.4. Преобразование координат
3.4.1. Преобразование координат на плоскости
Преобразование декартовой прямоугольной системы координат.
Параллельный перенос: 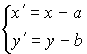 , ,
|
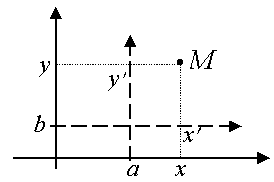 |
где координаты точки M в старой системе координат: ![]() ;
;
координаты точки M в новой системе координат: ![]() ;
;
координаты нового начала координат: ![]() .
.
Поворот: 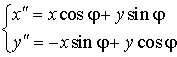 , ,
|
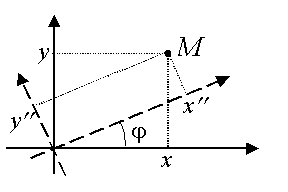 |
где координаты точки M в старой системе координат: ![]() ;
;
координаты точки M в новой системе координат: ![]() ;
;
угол поворота: j .
| Переход от декартовых прямоугольных координат 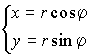 ; ; |
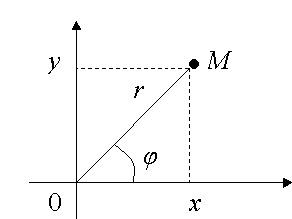 |
3.4.2. Преобразование координат в пространстве
Переход от декартовых координат ![]() к цилиндрическим координатам
к цилиндрическим координатам ![]() и обратно:
и обратно:
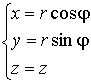 |
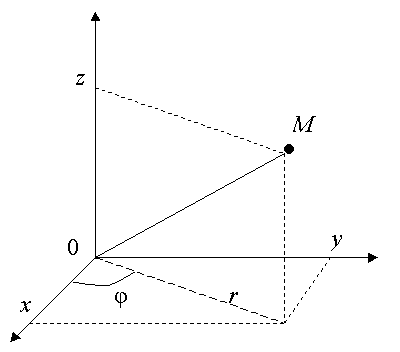 |
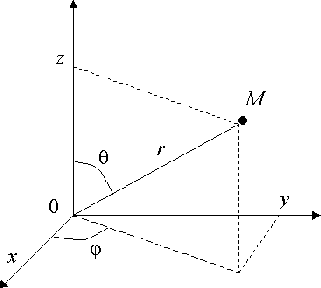
Переход от декартовых координат ![]() к сферическим координатам
к сферическим координатам ![]() и обратно:
и обратно:
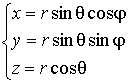 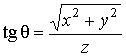 ; ; |
 |


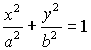 .
.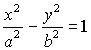 .
.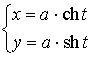
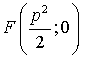 ;
;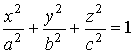 .
.