Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (7.4). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (7.4) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:

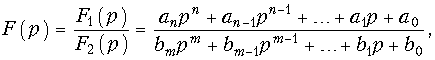
где 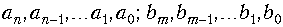— вещественные коэффициенты, причем F₁(p) и F₂(p) не имеют общих корней.

Для нахождения оригинала f(t) разложим F(p) на простые дроби:

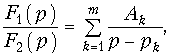
где p_k — простые корни характеристического уравнения

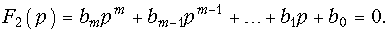
A_k — коэффициенты разложения.

Для того, чтобы найти коэффициент A_k домножим обе части (7.26) на (р — p_k) и перейдем к пределу:

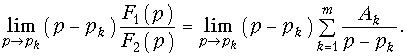
Раскрывая неопределенность в левой части равенства (7.28) по правилу Лопиталя и учитывая, что согласно (7.27) правая часть (7.28) равна A_k, получаем

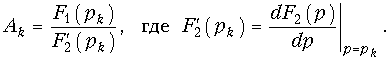
Подставив значения A_k в формулу (7.26), найдем:

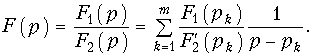
Если учесть, что изображение 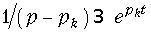(см. табл. 7.1), то на основании свойства линейности преобразования Лапласа окончательно получим:

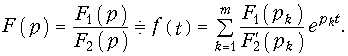
Формула (7.30) является математической формулировкой теоремы разложения и позволяет найти оригинал по изображению в виде (7.25), в случае простых корней. Если среди корней p_k имеется один нулевой корень, т. е. F₂(р) = pF₃(p), то теорема разложения примет вид

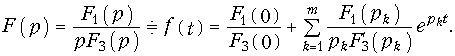
Формулу (7.31) можно получить, если подставить в (7.30) вместо F₂(р) значение pF₃(р) и осуществить операцию дифференцирования.

Если среди корней уравнения (7.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни p_k и p_k+1, то в формуле (7.30) достаточно взять p_k, а для p_k+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом действительности f(t) будет равна

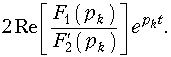
При этом в уравнении для f(t) появятся составляющие типа (6.9): .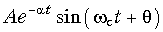

Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (7.25) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).

Пример. Задано изображение в виде

.

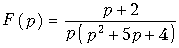Обозначим F₁(p) = p + 2; F₂(p) = p(p² + 5p + 4). При этом получим F(p) в виде (7.25). Найдем корни характеристического уравнения F₂(p) = p(p² + + 5p + 4) = 0.

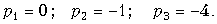
При этом F₁(p₁) = 2; F₁(p₂) = 1; F₁(p₃) = –2.

Определим производную

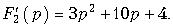
Отсюда F₂¢(p₁) = 4; F₂¢(p₂) = –3; F₂¢(p₃) = 12. Воспользовавшись формулой (7.30), окончательно получим:

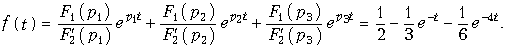
Учитывая, что среди корней характеристического уравнения F₂(p) = 0 имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим

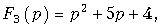
то получим

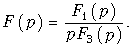
Тогда корни уравнения F₃(p) = 0 будут равны p₁ = —l, p₂ =—4. С учетом значений

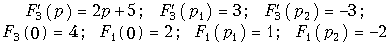
согласно (7.31) окончательно получим

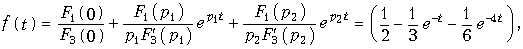
что полностью совпадает с ранее полученным решением.