Дискретная цепь может осуществлять любые операции: фильтрацию сигнала, корректирование характеристик и т.п., т.е. выполнять функции любой аналоговой цепи.
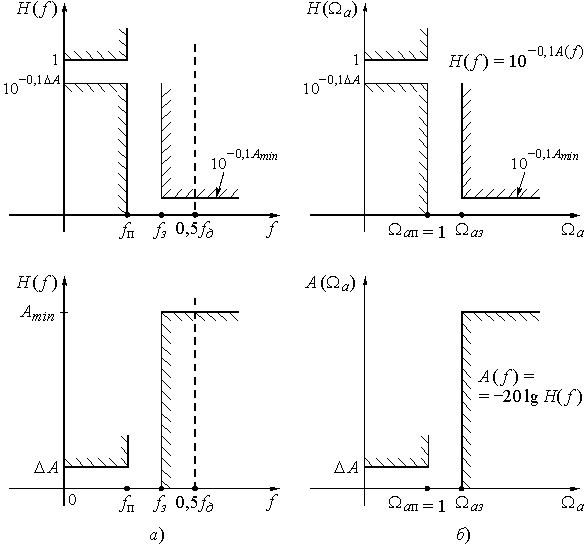
Рис. 58
В частности, при синтезе дискретных частотных фильтров нужно найти такие коэффициенты передаточной функции (19), (22) или (24), частотная характеристика которой удовлетворяла бы нормам ослабления фильтра в полосах пропускания и непропускания (рис. 58,а). Определение коэффициентов - это задача аппроксимации. Известен целый ряд методов ее решения. Наиболее распространенным является следующий метод. Сначала рассчитывают аналоговый НЧ-прототип и получают его передаточную функцию ![]() , затем путем замены комплексной переменной
, затем путем замены комплексной переменной ![]() переходят от
переходят от ![]() к передаточной функции дискретной цепи
к передаточной функции дискретной цепи ![]() .
.
Использование стандартного преобразования ![]() или
или ![]() не приведет к дробно-рациональной функции. Поэтому для ФНЧ применяют билинейное преобразование
не приведет к дробно-рациональной функции. Поэтому для ФНЧ применяют билинейное преобразование
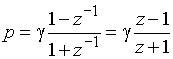 . (28)
. (28)
(g - некоторый постоянный множитель), которое является первым приближением стандартного преобразования при разложении его в ряд Тейлора:
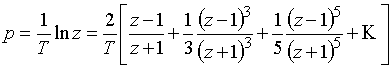 . (29)
. (29)
Из разложения (29) следует, что необходимо выбирать ![]() . Однако, далее мы покажем, что удобнее брать другие значения коэффициента g.
. Однако, далее мы покажем, что удобнее брать другие значения коэффициента g.
Билинейное преобразование (28) переводит все точки из левой полуплоскости переменной p в точки на единичной окружности плоскости z. Так что, если была устойчива аналоговая цепь, будет устойчивой и дискретная. Подтвердим эти утверждения на примере.
Пример 20.1. Найдем положения точек на z-плоскости, соответствующих следующим значениям переменной p: ![]() ;
; ![]() = -2 + j2;
= -2 + j2; ![]() = j2.
= j2.
Из формулы (28) найдем выражение для расчета z:
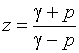 .
.
Подставляя в эту формулу значение полюса p =![]() = -2, лежащего в левой полуплоскости плоскости p, получаем
= -2, лежащего в левой полуплоскости плоскости p, получаем
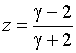 .
.
Поскольку g - число вещественное и положительное, то числитель (g - 2) меньше знаменателя (g + 2), и значит z< 1, т.е. точка z лежит внутри единичной окружности, что говорит об устойчивости цепи.
При p = ![]() = -2 + j2 получаем
= -2 + j2 получаем
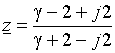 .
.
Найдем модуль z
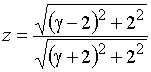 .
.
Он меньше единицы, поскольку модуль числителя меньше модуля знаменателя, т.е. точка z также лежит внутри единичной окружности.
При p =![]() = j2 получаем
= j2 получаем
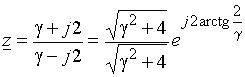 .
.
Модуль z равен 1, т.е. точка p = j2, лежащая на мнимой оси плоскости p, переходит в точку на единичной окружности плоскости z при использовании билинейного преобразования.
Переход к аналоговому прототипу применяется обычно для дискретных фильтров, имеющих бесконечную импульсную характеристику ![]() , принимающую ненулевые значения на бесконечном множестве значений n = 0, 1, ... .
, принимающую ненулевые значения на бесконечном множестве значений n = 0, 1, ... .
Дискретные цепи с конечной импульсной характеристикой, принимающей ненулевые значения лишь при n = 0, 1, ..., N - 1, не имеют аналогов среди пассивных электрических фильтров, поэтому для их расчета применяются другие методы.
Нерекурсивные фильтры с передаточной функцией (19) всегда имеют конечные импульсные характеристики. Рекурсивные фильтры с передаточными функциями (22) и (24) могут иметь как конечные, так и бесконечные импульсные характеристики.
Пример 20.2. Найдем дискретные импульсные характеристики фильтров, имеющих передаточные функции
![]() ,
, 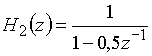 ,
,
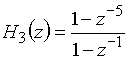 .
.
Дискретная импульсная характеристика ![]() - это обратноеz-преобразование передаточной функции
- это обратноеz-преобразование передаточной функции ![]() , т.е.
, т.е. ![]() . Нерекурсивной цепи с передаточной функцией
. Нерекурсивной цепи с передаточной функцией ![]() соответствует
соответствует ![]() = {2; 0,5; -3}, т.е. это фильтр с конечной импульсной характеристикой.
= {2; 0,5; -3}, т.е. это фильтр с конечной импульсной характеристикой.
Импульсная характеристика цепи с передаточной функцией ![]() рассчитывается по формуле
рассчитывается по формуле ![]() (см. пример 10.1), т.е. это рекурсивный фильтр с бесконечной импульсной характеристикой.
(см. пример 10.1), т.е. это рекурсивный фильтр с бесконечной импульсной характеристикой.
Отсчеты импульсной характеристики рекурсивной цепи с передаточной функцией ![]() будут конечными и равными 1 только для n = 0, 1, 2, 3, 4, а для n³ 5
будут конечными и равными 1 только для n = 0, 1, 2, 3, 4, а для n³ 5 ![]() . Значит этот рекурсивный фильтр имеет конечную импульсную характеристику.
. Значит этот рекурсивный фильтр имеет конечную импульсную характеристику.
Самоконтроль
1. В чем суть задачи аппроксимации и метода ее решения для дискретных фильтров?
2. Какое билинейное преобразование применяется при расчете дискретных фильтров?
3. Почему при использовании билинейного преобразования устойчивой аналоговой цепи соответствует устойчивая дискретная цепь?
4. Докажите, что дискретная цепь неустойчива, если полюс передаточной функции соответствующей аналоговой цепи лежит в правой полуплоскости плоскости p, т.е. p = a + jw, a> 0.
5. Что такое конечная (и бесконечная) импульсная характеристика?
6. Какая импульсная характеристика у нерекурсивных (у рекурсивных) фильтров: конечная или бесконечная?

