Требования к любому типу фильтра преобразуются в требования к аналоговому ФНЧ-прототипу. Затем рассчитывается аналоговый прототип, как это показано выше, и с помощью замены переменных переходят от ![]() к
к ![]() .
.
Конечно, формулы замены переменных уже не такие, как для ФНЧ. Они приведены для разных типов фильтров в табл. 2. Требования к дискретным фильтрам графически изображены на рис. 64.
Пример 25.1. Определить передаточную функцию дискретного полосового фильтра с параметрами: ![]() = 140 Гц;
= 140 Гц; ![]() = = 15,5 Гц;
= = 15,5 Гц; ![]() = 30 Гц;
= 30 Гц; ![]() = 7,75 Гц;
= 7,75 Гц; ![]() = 60 Гц;
= 60 Гц; ![]() = 0,5 дБ;
= 0,5 дБ; ![]() = 40 дБ.
= 40 дБ.
Определяем:
![]() = 15,5/140 = 0,110714;
= 15,5/140 = 0,110714; ![]() = 30/140 = 0,214286;
= 30/140 = 0,214286;
![]() = 7,75/140 = 0,055357;
= 7,75/140 = 0,055357; ![]() = 60/140 = 0,428571;
= 60/140 = 0,428571;
![]() = 2,964087;
= 2,964087;
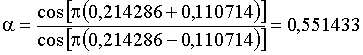 ;
;
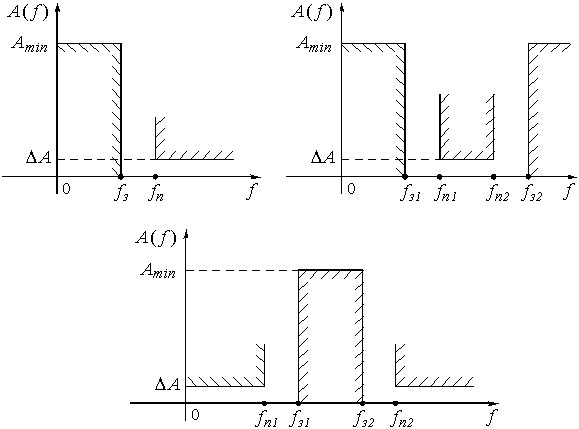
Рис. 64
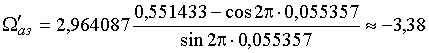 ;
;
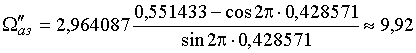 ;
;
![]() .
.
По данным ![]() = 3,38, DА = 0,5 дБ и
= 3,38, DА = 0,5 дБ и ![]() =40 дБ из справочника находим
=40 дБ из справочника находим
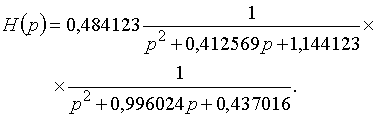
Передаточную функцию ![]() найдем, используя подстановку
найдем, используя подстановку
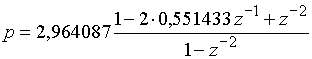
и разлагая каждый из двух полиномов четвертой степени (в знаменателе ![]() ) на множители (полиномы второй степени):
) на множители (полиномы второй степени):
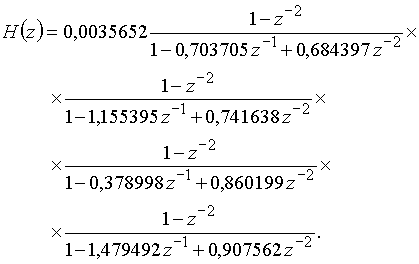
Самоконтроль
1. Каков порядок расчета дискретного фильтра верхних частот (полосового, режекторного)?
2. Какие формулы замены переменных (p и z) используются при расчете дискретного фильтра верхних частот (полосового, режекторного)?
3. Как рассчитать нормированную частоту аналогового дискретного фильтра верхних частот (полосового, режекторного), если известна соответствующая частота дискретного фильтра?

