Количественно помехоустойчивость определяется некоторой мерой соответствия принятого сообщения (сигнала) переданному. Эта мера (мера качества решения) из-за случайного характера помех всегда является статистической и определяется потребителем сообщения (степенью чувствительности потребителя к тем или иным искажениям).

Оптимальный приемник (оптимальное правило решения) обеспечивает наилучшее качество решения, то есть обеспечивает минимум искажений переданного сообщения в соответствии с мерой качества, заданной потребителем. Оптимальное значение меры качества, которое достигается приемником в процессе оптимизации, называется критерием оптимальности приема (или просто критерием качества).

При приеме дискретных сигналов в качестве меры помехоустойчивости обычно используется средний риск Rср, тогда критерием оптимальности является min {Rср};

Rср = 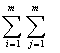Пij P (Si , yj), (2.1)

где P (Si , yj) - совмеcтная вероятность передачи S i и приема yj ;

Пij - функция потерь (риск потребителя) при приеме yj , когда передавался сигнал Si ; при этом i = j соответствует правильному приему (значения Пij =0), i ¹ j - ошибка (значения Пij > 0) ;

m - число передаваемых сигналов.

Приемник, работающий по этому критерию, называется байесовским, а правило решения - байесовским правилом.

Рассмотрим некоторые наиболее часто применяемые критерии при передаче двух сигналов S1(t) и S2(t), так как в технике связи такая задача встречается наиболее часто.

При различении сигналов обязательно возникают ошибки при любой мощности сигнала и помехи, так как из-за случайного характера помех возможны выбросы помехи значительной величины. На рис.2.1 приведен граф переходов в системе связи, когда передаются сигналы S1(t) и S2(t). Если передавался сигнал S1, а принят y1 - это означает, что первый сигнал принят правильно. Если же передавался сигнал S1, а принят у2 - это означает, что при приеме вместо первого сигнала получен второй сигнал - произошла ошибка.

Условные вероятности Р(у1/S1) и Р(у2/S2) есть вероятности правильного приема этих сигналов.

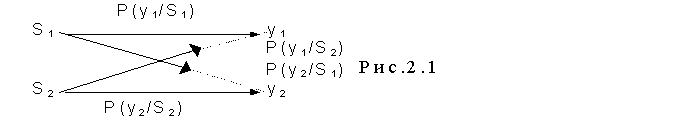
Существует несколько критериев помехоустойчивости при различении сигналов. Эти критерии фактически отличаются правилом решения, которые определяют положение границы подпространств (пунктир на рис.1.2), исходя из конкретных требований потребителя к качеству приема сигналов различного назначения.

1. Критерий минимального среднего риска.

Согласно (2.1) этот критерий для двух сигналов минимизирует средний риск

Rср = {П12Р(S1,y2) + П21Р(S2,y1) = П12Р(S1)Р(y2/S1) + П21Р(S2)Р(y1/S2) . (2.2)

В зависимости от значения функции потерь (в данном случае весовых коэффициентов П12 и П21) этот критерий может применяться в системах связи различного назначения с учетом тех потерь (или убытков), которые являются следствием искажения сигналов S1 и S2.

Например, если сигнал S1 - отсутствие тревоги, а S2 - сигнал тревоги (пожарная или охранная сигнализация), то Р(у2/S1) - это вероятность ложной тревоги, а Р(у1/S2) - вероятность пропуска сигнала тревоги. Если это система противопожарной сигнализации, то в результате ложной тревоги убытки составляют, например, 10 рублей (затраты на ложный выезд), а в результате пропуска тревоги (в результате чего может сгореть важный объект) убытки составляют миллион рублей. В этом случае весовые коэффициенты могут быть соответственно равны П12 =10, П21 = 106. Приемник должен принимать решение таким образом, чтобы получить min{Rср}. Очевидно, для этой цели границу подпространств (рис.1.2) целесообразно удалить от сигнала тревоги S2 за счет увеличения вероятности искажения сигнала S1, при этом уменьшится вероятность пропуска сигнала тревоги; в результате критерий min{Rср} обеспечит минимальные убытки системы противопожарной безопасности.

2. Критерий максимального правдоподобия (критерий МП).

Критерий МП получается из критерия минимального среднего риска, если принять, что П12 = 1/P(S1), П21 = 1/P(S2).

При этом оптимальный приемник принимает решение таким образом, что минимизируется значение

l п = P(y2/S1) + P(y1/S2) . (2.3)

Критерий МП иногда называется критерием минимума потерь информации, так как оптимальное правило решения в этом случае устанавливает границу подпространства (рис.1.2) так, чтобы уменьшить вероятность искажения того сигнала, вероятность передачи которого меньше (следовательно, этот сигнал содержит больше информации).

Критерий МП применяется в системах связи также в тех случаях, когда априорные вероятности Р(S1) и P(S2) неизвестны.

3. Критерий идеального наблюдателя.

Если весовые коэффициенты П12 = П21 =1, то критерий минимального среднего риска минимизирует среднюю вероятность ошибки

pош = P(S1)P(y2/S1) + P(S2)P(y1/S2) (2.4) и называется критерием идеального наблюдателя.

Критерий идеального наблюдателя широко применяется в системах связи, когда искажения любого сигнала одинаково нежелательны и совпадает с критерием МП, если вероятности Р(S1) = P(S2) = 0,5.

4. Критерий Неймана-Пирсона.

В некоторых системах передачи информации (системах радиолокации, некоторых системах сигнализации) имеется необходимость фиксирования (задания) одной из условных вероятностей Р(у1/S2) или Р(у2/S1). При этом оптимальный приемник принимает решение таким образом, чтобы минимизировать ту условную вероятность, которая не задана. Критерий оптимальности, который используется таким приемником называется критерием
Неймана-Пирсона.

Например, задана вероятность пропуска сигнала S1 , то есть Р(у2/S1) = a.. Тогда критерий Неймана-Пирсона требует минимизации условной вероятности Р(у1/S2), обеспечивая заданное значение a. Вероятность Р(у1/S2) обычно обозначается b, тогда (1-b) = Р(у2/S2) называется качеством решения. Правило решения Неймана-Пирсона обеспечивает (min b) или мах(1- b) при a = const.

Приемник при использовании критерия Неймана-Пирсона строится таким образом, чтобы получить достаточно малую вероятность пропуска cигнала(цели ) Р(у2/S1)=a.. С тем, что при этом может (несмотря на минимизацию b=Р(у1/S2)) оказаться много ложных тревог, приходится мириться. В этом и заключается сущность данного критерия.