Дискретная цепь считается неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на ее выходе бесконечно нарастающий отклик. Наоборот, дискретная цепь устойчива когда отклик на ограниченное воздействие также ограничен.
Известно, что у устойчивой аналоговой цепи полюсы передаточной функции располагаются в левой полуплоскости переменной p. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа z-преобразованием точки левой полуплоскости p-плоскости переходят в точки, лежащие внутри единичной окружности z-плоскости (рис. 20). Таким образом, полюсы передаточной функции устойчивой дискретной цепи располагаются внутри единичной окружности z-плоскости.
Пример 16.1. Определим устойчивость цепей, имеющих передаточные функции:
а) 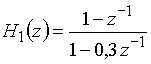 ,
,
б) 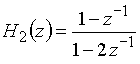 ,
,
в) 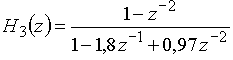 ,
,
г) 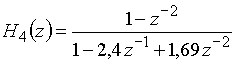 .
.
Полюс передаточной функции
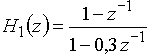
найдем, приравняв знаменатель ![]() к нулю,
к нулю, ![]() = 0.
= 0.
Получаем полюс ![]() = 0,3, который находится внутри единичной окружности z-плоскости. Это означает, что цепь устойчива.
= 0,3, который находится внутри единичной окружности z-плоскости. Это означает, что цепь устойчива.
Передаточная функция
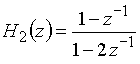
имеет полюс в точке ![]() = 2; такая цепь неустойчива.
= 2; такая цепь неустойчива.
Полюсы передаточной функции
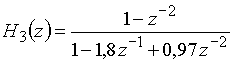
являются комплексно-сопряженными ![]() и
и ![]()
![]() . Поскольку эти полюсы лежат внутри единичной окружности (их модули
. Поскольку эти полюсы лежат внутри единичной окружности (их модули ![]() ), то данная дискретная цепь устойчива.
), то данная дискретная цепь устойчива.
Примером неустойчивой цепи служит цепь с передаточной функцией
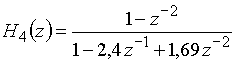 ,
,
у которой ![]() и
и ![]() и
и ![]() .
.
Пример 16.2. Дискретная цепь, являющаяся фильтром верхних частот с ослаблением в полосе непропускания (0 ¸ 500 Гц) более 36 дБ и с неравномерностью ослабления в полосе пропускания (выше 600 Гц) 1,25 дБ, при частоте дискретизации ![]() = 2,5 кГц имеет передаточную функцию
= 2,5 кГц имеет передаточную функцию
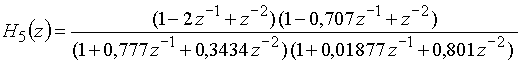 .
.
Ее полюсы ![]() и
и ![]() также лежат внутри области устойчивости. Заметим, что на нули таких ограничений нет: они оказались в точках z = 1 (двойной нуль) и
также лежат внутри области устойчивости. Заметим, что на нули таких ограничений нет: они оказались в точках z = 1 (двойной нуль) и ![]() , т.е. лежат на единичной окружности.
, т.е. лежат на единичной окружности.
Пример 16.3. Цифровой фильтр Баттерворта нижних частот 3-го порядка описывается передаточной функцией
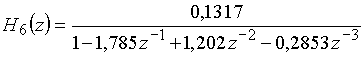 (25)
(25)
с полюсами ![]() и
и ![]() . Расположение полюсов в плоскости z показано на рис. 49, а). Здесь же приведена структурная схема такого фильтра (рис. 49, б). Цепь устойчива.
. Расположение полюсов в плоскости z показано на рис. 49, а). Здесь же приведена структурная схема такого фильтра (рис. 49, б). Цепь устойчива.
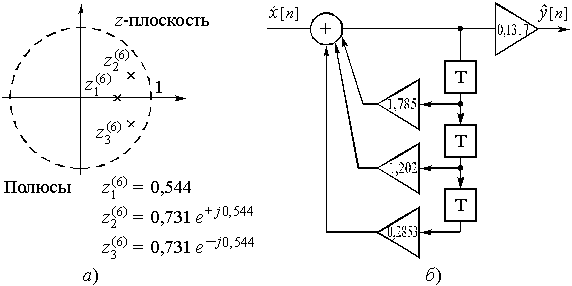
Рис. 49
Пример 16.4. Рассчитаем сигнал ![]() на выходе дискретной цепи, имеющей передаточную функцию
на выходе дискретной цепи, имеющей передаточную функцию 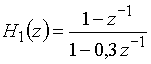 (см. Пример 16.1, а), если на вход подается сигнал
(см. Пример 16.1, а), если на вход подается сигнал ![]() = {3; 2; 1}.
= {3; 2; 1}.
Воспользуемся выражениями (23) и (24) для нахождения выходного сигнала ![]() в рекурсивной дискретной цепи с прямыми и обратными связями:
в рекурсивной дискретной цепи с прямыми и обратными связями:
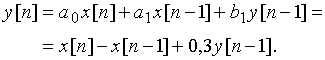
Рассчитаем значения выходного сигнала, подставляя значения ![]() в выражение для
в выражение для ![]() . Получаем выходную последовательность
. Получаем выходную последовательность ![]() = {3; -0,1; -1,03; -1,31: -0,39; -0,11; -0,03; -0,01; ...}. Таким образом, отклик
= {3; -0,1; -1,03; -1,31: -0,39; -0,11; -0,03; -0,01; ...}. Таким образом, отклик ![]() цепи с передаточной функцией
цепи с передаточной функцией ![]() на ограниченное воздействие также ограничен, т.е. цепь является устойчивой.
на ограниченное воздействие также ограничен, т.е. цепь является устойчивой.
Вывод: полюсы передаточной функции устойчивой дискретной цепи лежат внутри единичной окружности z-плоскости. Нерекурсивные цепи всегда устойчивы.
Самоконтроль
1. Какая дискретная цепь является устойчивой (неустойчивой)?
2. Где расположены полюсы передаточной функции устойчивой дискретной цепи?
3. Что можно сказать об устойчивости цепей с передаточными функциями
а) ![]() ,
,
б) 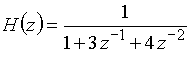 ,
,
в) 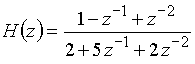 ?
?

