Средняя вероятность ошибки в соответствии с формулой (2.4) зависит от вероятности неправильного приема сигналов S1 и S2 . Однако при применении идеального приемника Котельникова канал связи предполагается симметричным, т.е. P(y2/S1) = P(y1/S2). Поэтому формула (2.4) упрощается. В нашем случае Pош = P(y2/S1). Эту формулу мы возьмем за основу при определении вероятности ошибки в приемнике Котельникова.
Допустим, нам известно, что на вход приемника поступает сигнал S1(t). В этом случае, в соответствии с правилом решения приемника Котельникова (4.4), должно выполняться следующее неравенство
[x(t) - S1(t)]2 < [x(t) - S2(t)]2 . (7.1)
Однако, несмотря на поступление сигнала S1(t), при сильной помехе знак неравенства может измениться на противоположный, в результате чего приемник вместо сигнала S1(t) выдает сигнал S2(t), то есть произойдет ошибка. Вероятность искажения сигнала S1(t) можно определить как вероятность изменения знака неравенства (7.1), если подставить туда x(t) = S1(t) + n(t).
После очевидных преобразований получаем
Pош = P(y2/S1) = P{n2(t) > [n(t) + S1(t) - S2(t)]2} =P{0 > 2 n(t) [S1(t) - S2(t)] + [S1(t) - S2(t)]2} =
= P{1/T ![]() 2n(t) [S1(t) - S2(t)]dt + 1/T
2n(t) [S1(t) - S2(t)]dt + 1/T ![]() [S1(t) - S2(t)]2dt < 0}.
[S1(t) - S2(t)]2dt < 0}.
Сокращая на Т, получаем
Pош = P{ ![]() n(t) [S1(t) - S2(t)]dt + 0,5
n(t) [S1(t) - S2(t)]dt + 0,5 ![]() [S1(t) - S2(t)]2dt < 0}.
[S1(t) - S2(t)]2dt < 0}.
Обозначим в этом выражении:
![]() n(t) [S1(t) - S2(t)]dt = m ,
n(t) [S1(t) - S2(t)]dt = m , ![]() [S1(t) - S2(t)]2dt = Еэ (7.2)
[S1(t) - S2(t)]2dt = Еэ (7.2)
С учетом этих обозначений вероятность искажения сигнала S1 будет определятся формулой
Pош = P{m < 1/2× Eэ}. (7.3)
В этой формуле Eэ - энергия разности сигналов S1(t) - S2(t), называемая "эквивалентной энергией" , а m - некоторая случайная величина, зависящая от помехи n(t) и разности сигналов S1(t) - S2(t).
Так как помеха n(t) имеет гауссовское распределение, а величина m есть результат линейной операции над n(t) , то и величина m распределена также по гауссовскому закону
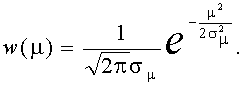
Тогда, в соответствии с (7.3)
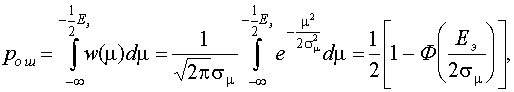 (7.4)
(7.4)
где 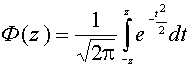 - табулированный интеграл вероятностей.
- табулированный интеграл вероятностей.
Можно доказать,что при флюктуационной помехе на входе приемника со спектральной плотностью помехи N0 дисперсия величины m определяется формулой s2m = N0Eэ /2.
Подставляя это значение s2m в (7.4) получим окончательно 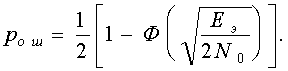 (7.5)
(7.5)
Таким образом, в приемнике Котельникова вероятность ошибки полностью определяется эквивалентной энергией сигналов и спектральной плотностью помехи и от полосы пропускания приемника не зависит. На практике обычно на входе приемника все-таки ставят полосовой фильтр, так как в канале связи, кроме флюктуационных помех, часто встречаются также другие помехи (от соседних каналов, импульсные и др.)
Формула (7.5) является достаточно общей. Для конкретных видов модуляции в канале связи эту формулу видоизменяют, для чего вычисляют соответствующее значение Eэ . При этом для различных видов модуляции Eэ определяют через энергию одного из сигналов, а в окончательную формулу вводят величину
h20 = E1/N0 . (7.6)
Следовательно, в приемнике Котельникова, который также называется когерентным (в приемнике известна фаза принимаемого сигнала) вероятность ошибки зависит не от отношения мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличить его энергию за счет увеличения его длительности, что дает дополнительные возможности в построении помехоустойчивых систем связи.

