1. Уравнение Шредингера - основное динамическое уравнение релятивистской квантовой механики. Оно играет такую же фундаментальную роль, как уравнение Ньютона в классической механике и уравнения Максвелла в классической теории электромагнетизма.

Уравнение Шредингера описывает изменение во времени состояния квантовых объектов, характеризуемое волновой функцией: . Если известна волновая функция в начальный момент времени, то решая уравнение Шредингера, можно найти в любой последующий момент времени t.

Для частицы массы m, движущейся в потенциальном поле U=U(r), временное уравнение Шредингера имеет вид:

,

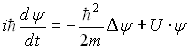где

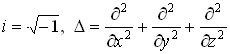
- оператор Лапласа, x, y, z – координаты.

Решение дифференциального уравнения есть - волновая функция, которая прямого физического смысла не имеет. Смысл имеет квадрат модуля волновой функции , как плотность вероятности обнаружения частицы (системы) в момент времени t в квантовом состоянии в точке пространства с координатами x, y, z в объеме .

Эта вероятностная интерпретация временной функции - один из основных постулатов квантовой механики.

2. Стационарное (не зависящее от времени) уравнение Шредингера имеет вид:

,

где W - полная, а (W-U) - кинетическая энергия частицы (системы). Потенциальная энергия в уравнении Шредингера не зависит от времени. Решением такого уравнения является функция вида:

.

Оператор Лапласа в сферических координатах имеет вид:

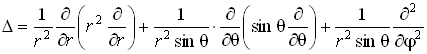
3. Зная -функцию, можно рассчитать поведение микрочастиц. Вероятность обнаружения частицы в объёме V определяется:

.

В одномерном случае вероятность найти частицу в интервале от X₁ до X₂ рассчитывается так:

4. Среднее значение любой характеристики микрочастицы вычисляется по формуле:

в одномерном случае:

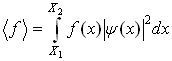
- величины, определяющие границы изменения величины x, они могут быть любые, включая и, и 0, и .

5. Если необходимо найти наиболее вероятное положение частицы в пространстве, то необходимо исследовать на экстремум функцию .

6. Функция , где - функция в комплексном виде, а -функция, сопряжённая . Возвращаясь к формуле (42), имеем:

Тогда ,

так как , то

не зависит от времени, что означает стационарное (независимое от t) состояние системы.

7. Для квантовых систем, движение которых происходит в ограниченной области пространства, решение уравнения Шредингера существует только для некоторых дискретных значений: нумерация которых определяется набором целых квантовых чисел. Значениям ряда соответствуют волновые функции Значения называются спектром собственных значений энергии, а соответствующие волновые функции - -спектром собственных функций. (i=1,2, …n).

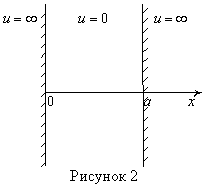
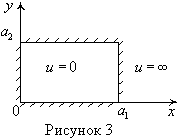
8. Частица массой m в бесконечной прямоугольной яме шириной .

Собственные волновые функции

,

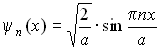где n - квантовое число, n=1,2,3….

Собственные значения энергии:

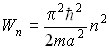
9. Гармонический осциллятор

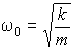- собственная частота;

- потенциальная энергия.

Собственные значения энергии

,

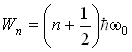где n=1,2…. - квантовое число, k- коэффициент жёсткости действующей упругой силы, m - масса частицы.

10. Движение квантовой частицы отличается от движения классической частицы. В квантовой механике существует конечная вероятность обнаружить частицу в классически запрещённой области пространства.

Потенциальный барьер - ограниченная в пространстве область высокой потенциальной энергии частицы в силовом поле. Если энергия частицы больше высоты потенциального барьера , то в квантовой механике существует ненулевая вероятность отражения частицы от такого барьера, хотя в классической физике частица при таких условиях двигается, не замечая барьера. При квантовая частица проходит (просачивается) сквозь потенциальный барьер. Такое явление называется туннельным эффектом. Вероятность прохождения частицей барьера называется коэффициентом прозрачности D.

Решая уравнение Шредингера для прямоугольного потенциального одномерного барьера высотой и шириной , получим коэффициент прозрачности : 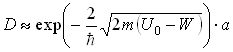(52)

Для потенциального одномерного барьера произвольной формы (рисунок 1):

и определяются при условии , где задается явной функцией координаты . Согласно рисунку равенство определяет координату , – координату . В формуле присутствует под знаком корня, где x – переменная, которая учитывается при интегрировании.

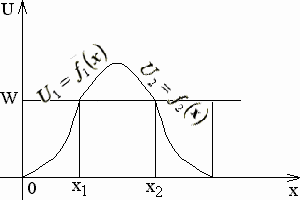
Рисунок 1

Движение в центрально-симметричном поле (примером является движение одного электрона в поле ядра с зарядом ). Если Z=1, то это атом водорода, при Z>1 – атом называется водородоподобным.

При решении этой задачи надо использовать уравнение Шредингера в сферических координатах. Потенциальная энергия в СИ имеет вид:

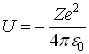(смотри раздел 4)

Собственные функции для описания поведения электрона в водородоподобных атомах:

где , –радиальная и угловая волновые функции, n, l, m – квантовые числа (главное, орбитальное, магнитное). При переходе в сферическую систему координат элемент объема

Пределы полного изменения параметров от до ; – от до ; – от до .

Вероятность обнаружения электрона в шаровом слое от до от ядра равна

.

Тогда плотность вероятности расположения в шаровом слое толщиной равна

.

И при определении наиболее вероятного расстояния электрона до ядра на экстремум исследуют именно функцию .