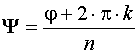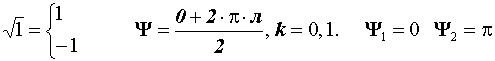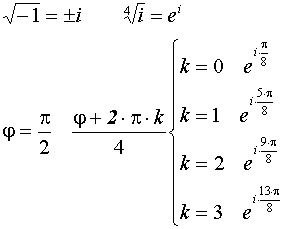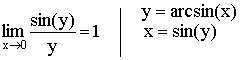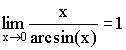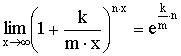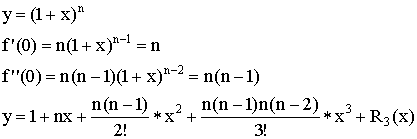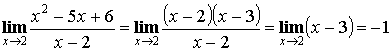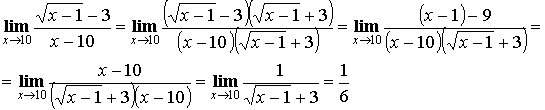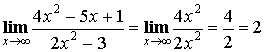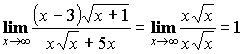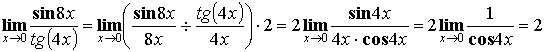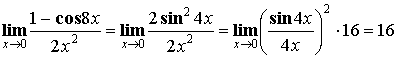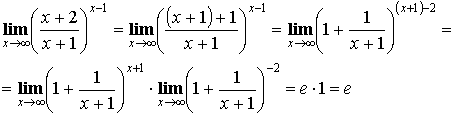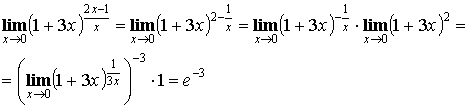1. Введение в анализ. Теория пределов
1.2. Функция, способы задания, простейшие свойства
2. Дифференциальное исчисление
2.1. Производная функции, её физический и геометрический смысл
2.2. Правила дифференцирования
2.4. Основные теоремы дифференциального исчисления
2.6. Монотонность, экстремумы функции
3.1. Понятие первообразной и неопределенный интеграл
3.3. Основные методы интегрирования
1. Введение в анализ
1.1. Комплексные числа (КЧ)
Комплексным числом z называется выражение z = a+bi, где ![]() , i – мнимая единица. i 2 = –1.
, i – мнимая единица. i 2 = –1.
a – действительная часть КЧ или a = Re z.
b – мнимая часть КЧ или b = Im z.
0+bi = bi - чисто мнимое число
a + 0i = a - действительное число
|
0 + 1i = i |
1 + 0i = 1 |
0 + 0i = 0 |
|
мнимая единица |
обычная единица |
обычный нуль |
Z1 = a1 + b1i
Z2 = a2 + b2i
![]()
Действия над КЧ
Z1 ![]() Z2 = (a1
Z2 = (a1 ![]() a2) + (b1
a2) + (b1 ![]() b2)
b2)![]() i – сложение/вычитание КЧ.
i – сложение/вычитание КЧ.
Возведение в степень мнимой единицы:
i1 = i i2 = – 1 i3 = i i4 = 1
Z1 ![]() Z2 = (a1 + b1
Z2 = (a1 + b1![]() i)
i)![]() (a2 + b2
(a2 + b2![]() i) = a1
i) = a1![]() a2 + a1
a2 + a1![]() b2
b2![]() i
i
+ a2![]() b1
b1![]() i
i
+ b1![]() b2
b2![]() i2 =
i2 =
= (a1![]() a2 – b1
a2 – b1![]() b2) + (a1
b2) + (a1![]() b2 + a2
b2 + a2![]() b1)
b1)![]() i – произведение КЧ.
i – произведение КЧ.
Сопряженным числом (![]() ) для данного комплексного числа называется число, которое отличается только знаком мнимой части от данного числа.
) для данного комплексного числа называется число, которое отличается только знаком мнимой части от данного числа.
![]()
Пример: ![]()
![]()
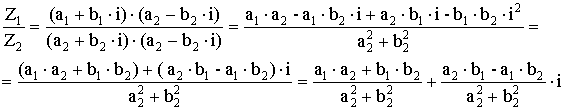 – деление КЧ.
– деление КЧ.
Пример:
![]()
Комплексная плоскость
Z = a + bi – алгебраическая форма записи КЧ.
Модуль КЧ
![]()
Аргумент КЧ
Аргумент КЧ – ![]() .
.
Полярная система координат
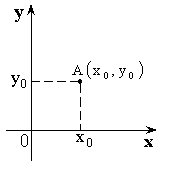
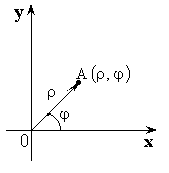
Декартова система. Полярная система
![]() – полярный радиус,
– полярный радиус, ![]() – полярный угол,
– полярный угол, ![]() – полярные координаты.
– полярные координаты.
![]()
![]()
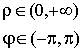
![]() ;
; ![]()
![]()
Пример:
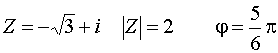
![]()
![]() – тригонометрическая форма записи КЧ.
– тригонометрическая форма записи КЧ.
Примеры:
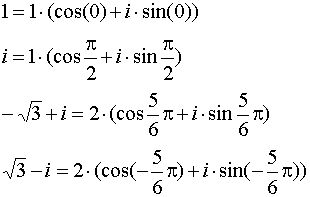
Формула Эйлера
|
|
– Формула Эйлера |
|
|
|
– взаимосвязь между e, i и |
![]() – показательная форма КЧ.
– показательная форма КЧ.
![]()
КЧ не сравнивают между собой. Множество КЧ не упорядоченно.
Возведение в степень КЧ
![]()
При возведении в степень модуль возводиться в эту степень, а аргумент умножается на показатель степени.
Формула Муавра
![]()
Возведение во 2 – ю и 3 – ю степень по формуле Муавра:
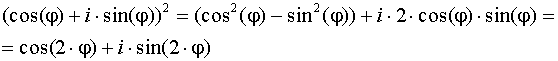
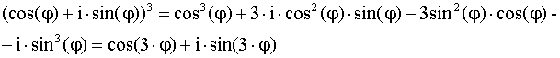
Используя равенство КЧ, получим: 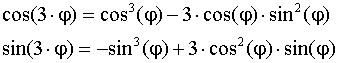 s
s
Извлечение корня из КЧ
![]()
![]()
![]()
![]()
|
|
k = 0, 1…,n – 1. |
Корень n – ой степени из КЧ имеет n различных значений.
Примеры:
Все корни n-ой степени из единицы находятся на единичной окружности и делят эту окружность на n равных частей.
1.2. Функция, способы её задания, простейшие свойства
Основные обозначения:
N – натуральные числа,
Q – рациональные(дробные),
Z – целые числа,
R – действительные числа;
![]()
Счетное множество – это множество, элементы которого можно пересчитать.
![]() – счетные и имеют одинаковую мощность
– счетные и имеют одинаковую мощность
R – несчетное множество.
 Множество действительных чисел всюду плотно на числовой оси.
Множество действительных чисел всюду плотно на числовой оси.
 [a, b] – замкнутый интервал, (a, b) – открытый интервал
[a, b] – замкнутый интервал, (a, b) – открытый интервал
Окр [x0] – окрестность точки x0 , любой открытый интервал, содержащий x0.
Окр [x0] = (a, b), где (a, b) содержит x0 – это окрестность.
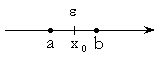 ax0 = x0b,
ax0 = x0b, ![]() – окрестность x0
– окрестность x0
Кванторы
1) ![]() – кванты всеобщности;
– кванты всеобщности;
2) ![]() – кванты существования.
– кванты существования.
|x – x0| – расстояние от точки x до точки x0
Числовой функцией называется соответствие между числовыми множествами X![]() Y, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.
Y, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.
![]()
![]()
![]()
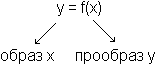
У каждого прообраза всегда один образ, у каждого образа может быть много прообразов.
Взаимнооднозначная функция – это когда разные x имеют разные y.
Способы задания функций:
а) аналитический;
б) графический;
в) табличный;
г) алгоритмический.
Функции делятся на 2 класса
- Элементарные
- Неэлементарные (специальные).
Элементарные функции изучаются в школьной математике и делятся на:
- Основные элементарные функции
а) степенные y = xn
б) показательные y = ax
в) тригонометрические y = sin x и другие.
- Элементарные, полученные из основных с помощью арифметических операций и операции получения сложной функции (операции композиции).
f
X Y
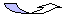
f -1 (обратная функция)
Обратные к показательным функциям – логарифмические функции. Обратные к тригонометрическим
Пример:
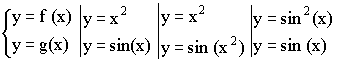
y = f (g(x)) – сложная функция – композиция элементарных функций.
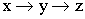
Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции.
Г(f) – график функции. График функции есть множество точек (x, y), где y = f(x).
Общие свойства функций
- Четность –
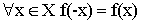
- Нечетность –
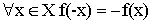
- Периодичность –
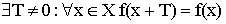
f(x) – ограниченная сверху, если ![]()
f(x) – ограниченная снизу, если ![]()
f(x) – ограниченная, если ![]()
f(x) – монотонная, если она постоянно возрастает или постоянно убывает
Если y = f(x), то Д – область определения данной функции.
Свойства модулей суммы и разности
1.3. Предел функции. Свойства пределов
Число b называется пределом функции в точке а, если для любой ![]() – окрестности точки b существует
– окрестности точки b существует ![]() – окрестность точки а.
– окрестность точки а.
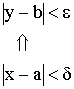
![]()
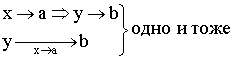
![]() – предел функции при
– предел функции при ![]() , равный b.
, равный b.
Число b называется пределом функции при неограниченном возрастании аргумента ![]() .
.
Для любого ![]() существует такое N, и если
существует такое N, и если ![]() , то
, то ![]() .
.
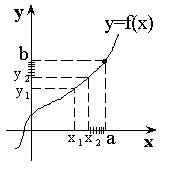
Примеры:
y = f(x) = ![]()
![]()
y = f(x) = x2 ![]()
Пример:
y =![]() , когда
, когда ![]() ,
, ![]()
Неопределенности: 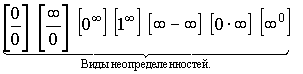
Раскрытие неопределенностей.
Теорема об ограниченности функции, имеющей предел
Если функция f(x) имеет предел в точке a ![]() , то она ограниченна в некоторой окрестности точки a.
, то она ограниченна в некоторой окрестности точки a.
Доказательство:
Пусть ![]() , тогда
, тогда ![]() , отсюда получаем
, отсюда получаем ![]() .
.
Обратное неверно.
Контрольный пример:
![]() в окрестности точки 0.
в окрестности точки 0.
![]() – не существует.
– не существует.
Бесконечно малой величиной при ![]() называется функция, предел которой в точке a равен 0.
называется функция, предел которой в точке a равен 0.
![]()
![]() – бесконечно малая величина (б.м.в.).
– бесконечно малая величина (б.м.в.).
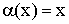 – бесконечно малая величина при
– бесконечно малая величина при 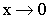
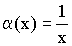 – бесконечно малая величина при
– бесконечно малая величина при 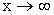
s
Бесконечно большой величиной при ![]() называется функция неограниченно возрастающая.
называется функция неограниченно возрастающая.
![]()
![]() – бесконечно большая величина (б.б.в.)
– бесконечно большая величина (б.б.в.)
Любая бесконечно большая величина неограниченна.
Теорема о связи предела и бесконечно малой величины
Если ![]() , то
, то ![]() , где
, где ![]() – бесконечно малая величина. Или
– бесконечно малая величина. Или ![]() .
.
Доказательство:
Допустим, что ![]() , тогда
, тогда 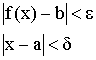 .
.
![]() , значит
, значит ![]() ,
, ![]() – бесконечно малая величина.
– бесконечно малая величина.
Пример:
f(x) = x2 + 1
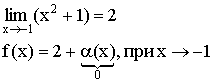
Теорема о связи бесконечно малой и бесконечно большой величиной
Если ![]() – бесконечно малая величина при
– бесконечно малая величина при ![]()
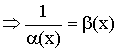 – бесконечно большая величина.
– бесконечно большая величина.
Если ![]() – бесконечно большая величина при
– бесконечно большая величина при ![]()
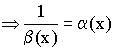 – бесконечно малая величина.
– бесконечно малая величина.
Доказательство:
Допустим, что ![]() – бесконечно малая величина при
– бесконечно малая величина при ![]() , то
, то ![]() , что
, что ![]() .
.
Значит ![]()
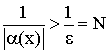
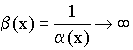
Следствие: 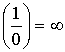 и
и 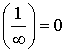
Свойства бесконечно малых величин
1) Алгебраическая сумма бесконечно малых величин есть бесконечно малая: ![]()
Доказательство:
![]()
![]() или
или ![]() , значит
, значит ![]() – бесконечно малая величина.
– бесконечно малая величина.
2) Произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая: ![]() , где f(x) – ограниченная.
, где f(x) – ограниченная.
Доказательство:
![]()
![]() , значит
, значит ![]() – бесконечно малая величина.
– бесконечно малая величина.
3) Частное от деления бесконечно малой величины на любую функцию, предел которой не равен 0, есть бесконечно малая: 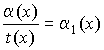 при
при ![]() и
и ![]() .
.
Теоремы о пределах
Теорема 1. Предел суммы равен сумме пределов, если они существуют: ![]()
Доказательство:
![]()
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
![]()
![]()
![]()
Получаем ![]()
![]()
Теорема 2. Предел произведения равен произведению пределов, если они существуют: ![]()
Доказательство:
![]()
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
![]()
![]()
![]()
Получаем ![]()
![]()
![]()
Теорема 3. Предел частного равен частному пределов: 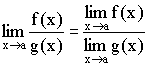 .
.
При условии: все пределы существуют и ![]() .
.
Доказательство:
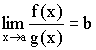
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
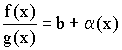
![]() ;
;
Получаем: 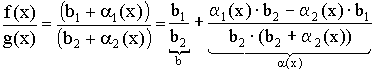
![]()
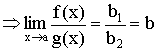
Теорема 4. Предел сохраняет знак неравенства. Если ![]()
![]() .
.
Доказательство:
![]()
Следовательно, ![]()
![]()
Следствие:
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел: ![]()
Теорема 6. Критерий Коши.
Если ![]() , тогда и только тогда
, тогда и только тогда ![]() .
.
Приемы раскрытия неопределенностей.
1) Выделение общего множителя (для неопределенности ![]() ).
).
Пример:
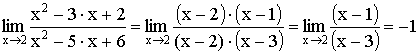
2) Умножение на сопряженное выражение (для неопределенности ![]() ).
).
Пример:
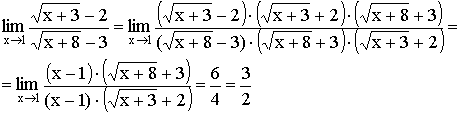
3) Выделение главной части (для неопределенности ![]() ).
).
Примеры:
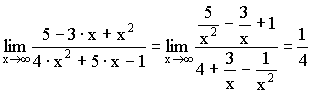
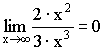 ;
;
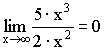
Теорема. Первый замечательный предел ![]() .
.
Доказательство (геометрическое):
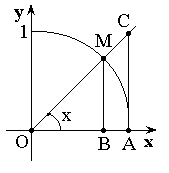
![]()
![]()
![]()
![]()
![]()
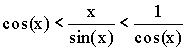
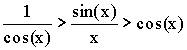
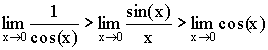
Так как 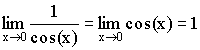 ,
,
то ![]() .
.
Следствия из теоремы:
1)
2)
3)
4)
5)
Теорема. Второй замечательный предел 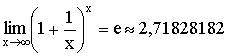 .
.
Доказательство:
Бином Ньютона:
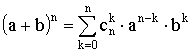 ,
,
где 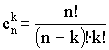 .
.
Используем бином Ньютона для доказательства неравенства: 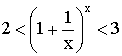
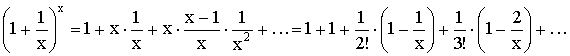
Отсюда заключаем, что 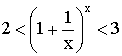 ,
,
а значит 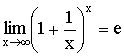 .
.
Следствия из теоремы:
1)
2)
3)
4)
Доказательство:
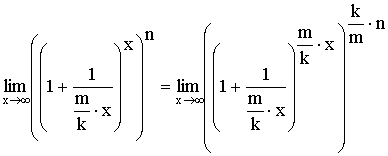
Если принять, что ![]() ,
,
то 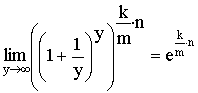
Примеры:
1) 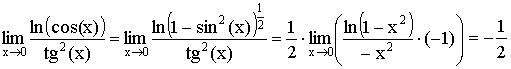
Учитывая, что ![]() .
.
2) ![]()
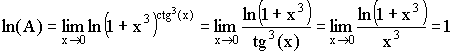 . Отсюда A = e.
. Отсюда A = e.
Учитывая, что ![]() .
.
Сравнение бесконечно малых величин (б.м.в.)
Пусть ![]() – бесконечно малые величины при
– бесконечно малые величины при ![]() , т.е.
, т.е. ![]() .
.
Определение 1. Если 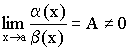 , то
, то ![]() – б.м.в. одного порядка малости.
– б.м.в. одного порядка малости.
Определение 2. Если 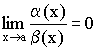 , то
, то ![]() – б.м.в. более высокого порядка, чем
– б.м.в. более высокого порядка, чем ![]() .
.
![]() –
– ![]() более высокого порядка, чем
более высокого порядка, чем ![]() ("о" – читается как "о малое").
("о" – читается как "о малое").
![]() –
– ![]() более низкого порядка, чем
более низкого порядка, чем ![]() ("О" – читается как "О большое").
("О" – читается как "О большое").
Определение 3. Если 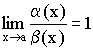 , то
, то ![]() и
и ![]() эквивалентны –
эквивалентны – ![]() .
.
Следствие из определения 3: ![]() при
при ![]() .
.
Теорема. Если ![]() и
и ![]() эквивалентны (
эквивалентны (![]() ), то
), то ![]() и
и ![]() .
.
Доказательство:
Пусть ![]() – бесконечно малые величины при
– бесконечно малые величины при ![]() и они эквивалентны (
и они эквивалентны (![]() ).
).
Тогда 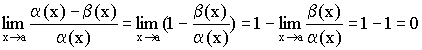 .
.
1.4. Непрерывность функции в точке и на интервале
Определение 1.
Пусть функция ![]() определена в окрестности точки
определена в окрестности точки ![]() , тогда функция непрерывна в
, тогда функция непрерывна в ![]() , если
, если ![]() .
.
Определение 2.
Функция ![]() непрерывна, если
непрерывна, если![]() .
.
Определение 3.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если
, если ![]() .Приращение аргумента
.Приращение аргумента ![]() . Приращение функции
. Приращение функции ![]() .
.
Определение 4. Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если
, если ![]() .Если функция не является непрерывной в точке
.Если функция не является непрерывной в точке ![]() , то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).
, то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).
Определение 5.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() справа, если
справа, если ![]() .
.
Определение 6.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() слева, если
слева, если ![]() .
.
Функция непрерывна на отрезке ![]() , если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.
, если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.
Теоремы о непрерывных функциях
Теорема 1. Сумма, произведение и частное непрерывных функций – непрерывны (кроме случая, когда знаменатель обращается в нуль).
Доказательство:
Пусть ![]() и
и ![]() .
.
Тогда ![]() .
.
Доказательство для умножения и деления аналогично доказательству для сложения.
Теорема 2. Композиция непрерывных функций непрерывна:
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если g(x) непрерывна в точке
, если g(x) непрерывна в точке ![]() и f(y) непрерывна в
и f(y) непрерывна в ![]() .
.
Теорема 3. Все элементарные функции непрерывны в своей области определения.
Разрывы функции
Разрыв первого рода
Пусть ![]() и
и ![]() существуют:
существуют:
I. Если ![]() , то в точке
, то в точке ![]() функция
функция
испытывает разрыв скачок первого рода.
Примеры:
-
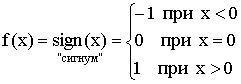
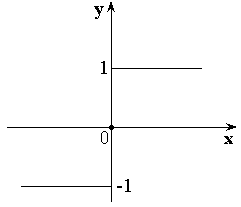
 – целая часть числа x.
– целая часть числа x.
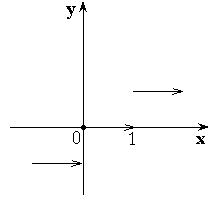
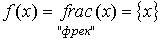 – дробная часть от числа x.
– дробная часть от числа x. 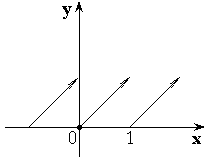
II. Если ![]() , то в точке
, то в точке ![]() функция испытывает устранимый разрыв первого рода.
функция испытывает устранимый разрыв первого рода.
Примеры:
1) 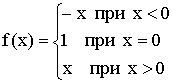
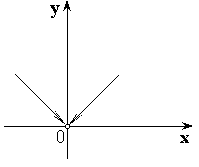
2) 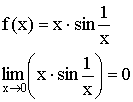
3) 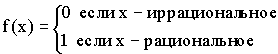
4) 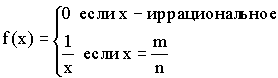
Разрыв второго рода
Функция испытывает разрыв второго рода, если ![]() – не существует.
– не существует.
Свойства функции, непрерывной на замкнутом отрезке
Пусть функция ![]() непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке ![]() .
.
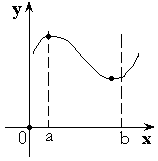
Теорема 1. Функция принимает наибольшее и наименьшее значение на ![]() .
.
Или ![]() , где
, где ![]() .
.
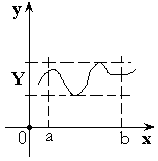
Теорема 2. Функция принимает все свои промежуточные
значения на ![]() .
.
Или ![]() , где
, где ![]() – область значений.
– область значений.
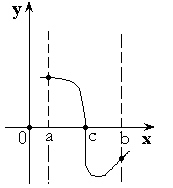
Теорема 3. Если функция принимает на концах отрезка ![]() значения разных знаков, то внутри отрезка найдется точка, в которой
значения разных знаков, то внутри отрезка найдется точка, в которой ![]() .
.
Или ![]() .
.
2. Дифференциальное исчисление
2.1. Производная функции. Её физический и геометрический смысл
Пусть функция ![]() определенна в окрестности точки
определенна в окрестности точки ![]() .
.
Тогда 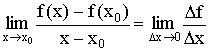 , где
, где ![]() и
и ![]() .
.
Производная функции в точке есть предел отношения приращения функции (![]() ) и приращения аргумента (
) и приращения аргумента (![]() ), когда
), когда ![]() .
.
Дифференцируемость
Механический смысл производной
Производная – это скорость изменения функции.
Геометрический смысл производной
Производная – это тангенс наклона угла касательной к график функции в данной точке к оси ![]() .
.
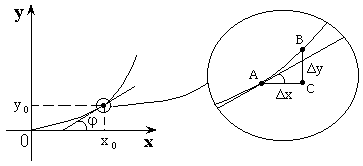
![]() ;
;
![]()
![]() при
при ![]()
Вычисление производной
Теорема. Если функция дифференцируема в точке, то она непрерывна в этой точке.
Доказательство:
![]()
![]() при
при ![]()
![]()
![]() при
при ![]() , следует
, следует ![]()
Обратное неверно.
Пример:
1) ![]()
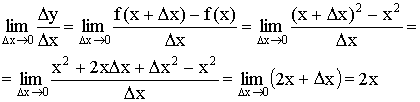
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; 
Таблица производных
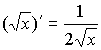 |
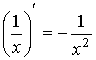 |
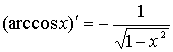 |
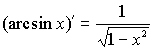 |
2.2. Правила дифференцирования
1) Производная от суммы равна сумме производных: 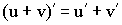
Доказательство:
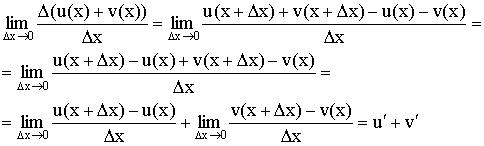
2) Постоянный множитель выносится за знак производной: ![]() .
.
3) Производная произведения: ![]() .
.
Доказательство:
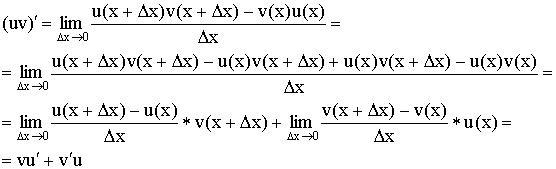
4) Производная дроби: 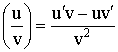 .
.
Доказательство:
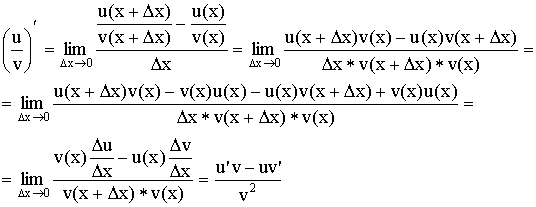
Вывод формул для производных
1) ![]()
2) 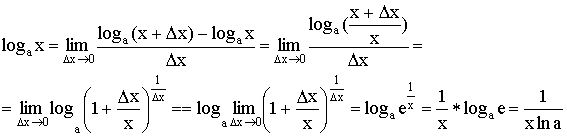
3) 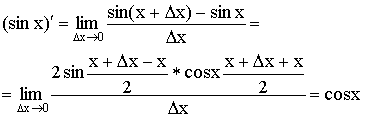
4) 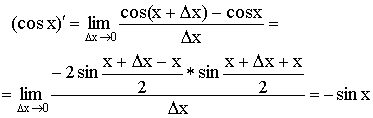
5) 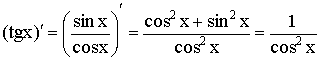
6) 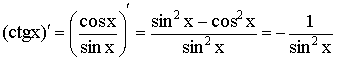
7) 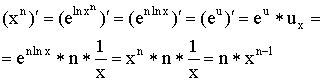
8) ![]()
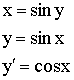
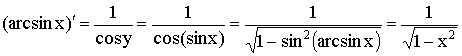
9) 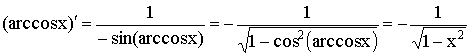
10) 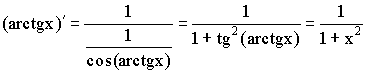
11) 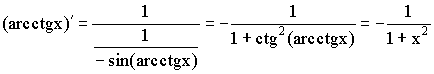
Теорема о производной сложной функции
Теорема. Доказательство:
Пусть ![]() , определена и непрерывна в окрестности точки (
, определена и непрерывна в окрестности точки (![]() , определена и непрерывна в окрестности точки
, определена и непрерывна в окрестности точки ![]() . Тогда
. Тогда ![]() .
.
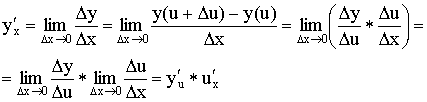
Это верно при условии, что каждая из функций дифференцируема.
Теорема о производной обратной функции
Теорема. Доказательство:
Пусть ![]() дифференцируемая в точке (
дифференцируемая в точке (![]() ).
).![]() - обратная к
- обратная к ![]() . Обратная функция существует если
. Обратная функция существует если ![]() монотонная функция. Тогда
монотонная функция. Тогда 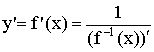
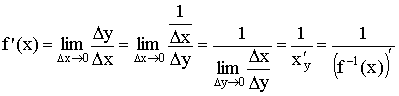
Производная сложной степенной функции
![]()
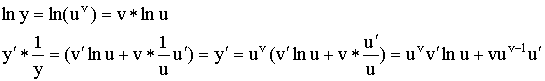
Прием логарифмического дифференцирования.
Производная неявной функции
![]() – общий вид неявно заданной функции.
– общий вид неявно заданной функции.
![]()
![]()
![]()
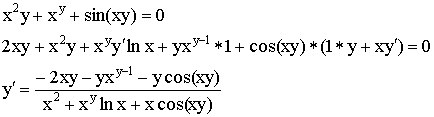
Производная параметрически заданной функции
Примеры параметрических функций:
1) 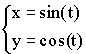
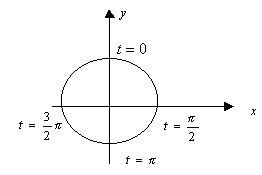
2) 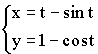

3) 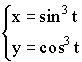
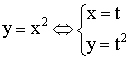
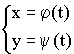
![]() – дифференцируемы.
– дифференцируемы.
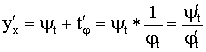
Пример:
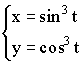
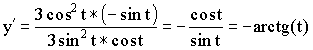
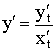
Гиперболические функции
| arsh x (ареа синус) | |
| arсh x (ареа косинус) | |
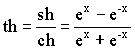 (гиперболический тангенс) (гиперболический тангенс) |
arth x (ареа тангенс) |
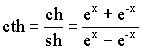 (гиперболический котангенс) (гиперболический котангенс) |
arcth x (ареа котангенс) |
![]()
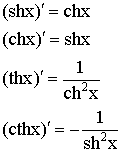
Схематичные графики гиперболических функций:
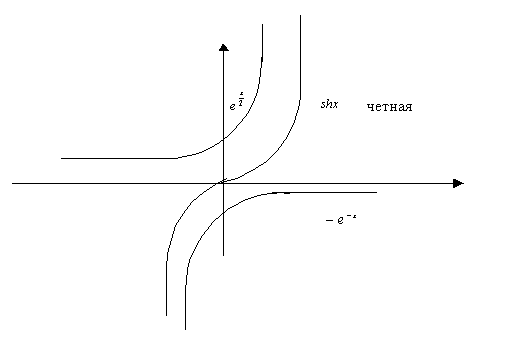
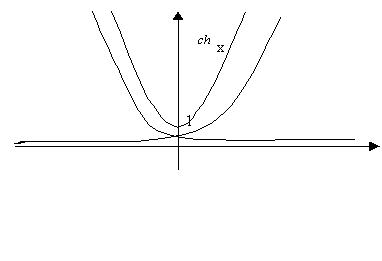
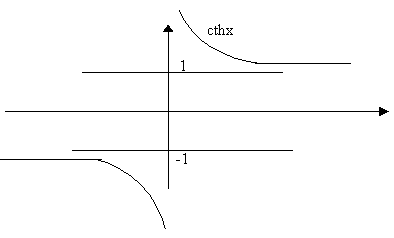
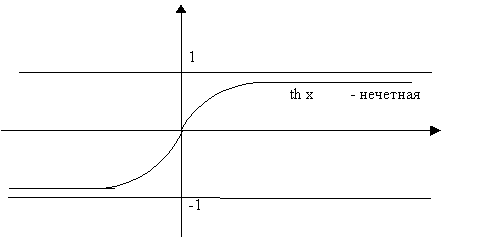
Производные высших порядков
Механический смысл второй производной – это ускорение.
Геометрический смысл второй производной – отвечает за вогнутость или выпуклость графика функции.
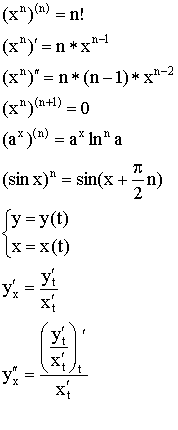
2.3. Дифференциал
![]() – гладкая, непрерывная и дифференцируемая.
– гладкая, непрерывная и дифференцируемая.
![]()
![]()
![]()
Дифференциалом называется главная (линейная) часть приращения функции.
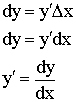 если
если 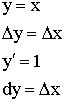
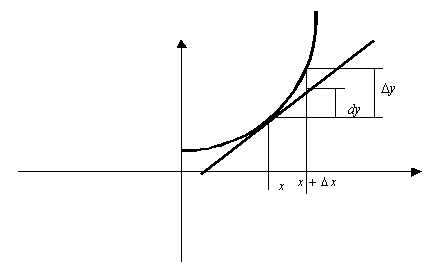
Свойства дифференциала:
1) ![]()
2) ![]()
3) ![]()
4) 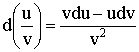
Доказательство для ![]() :
:
![]()
Остальные доказываются аналогично.
Инвариантность формы дифференцирования
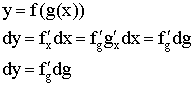
![]()
Форма дифференциала функции (производная умножить на дифференциал аргумента), не зависит от того, является ли аргумент функции независимой переменной или функций другого аргумента.
2.4. Основные теоремы дифференциального исчисления
Теорема Ролля, теорема о корнях производных
Доказательство:
Пусть ![]() гладкая на
гладкая на ![]() ,
, ![]() .
.
Тогда ![]()
![]()
![]()
![]() :
: ![]()
Любая гладкая функция, имеющая на концах отрезка одинаковые значения имеет, внутри этого отрезка, хотя бы один корень производной.
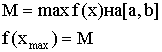
![]() при
при ![]()
![]() при
при ![]()
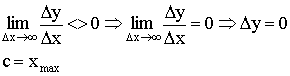
![]()
Теорема Коши о среднем
Доказательство:
Пусть ![]() - гладкие на
- гладкие на ![]() .
.
![]() на
на ![]()
Тогда ![]()
![]()
![]() :
: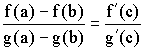 , где
, где ![]() .
.
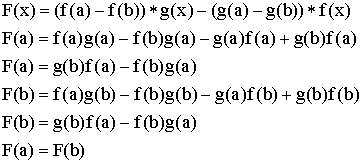
F – гладкая на отрезке ![]() .
.
По теореме Ролля ![]()
![]() :
: ![]() .
.
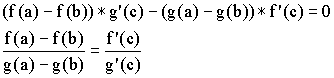
![]() по условию, а
по условию, а ![]() так как иначе по теореме Ролля
так как иначе по теореме Ролля ![]() , что противоречит условию.
, что противоречит условию.
Теорема Логранжа. Теорема о конечных приращениях
Доказательство:
Пусть ![]() гладкая на
гладкая на![]() ,
,
Тогда ![]()
![]()
![]()
![]() :
: ![]() .
.
Пусть ![]() :
:
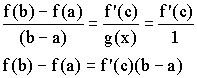
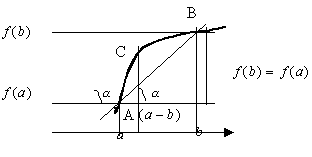
Геометрический смысл
Для любой гладкой на замкнутом отрезке кривой найдется точка, в которой касательная параллельна хорде AB.
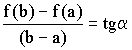
Правило Лопиталя (теорема Вернули – Лопиталя)
Пусть ![]() и
и ![]() гладкие в окрестности
гладкие в окрестности ![]() и
и ![]()
Тогда 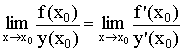
Правило Лопиталя: Предел отношения функций равен пределу отношения их производных.
Доказательство:
Применим теорему для ![]() и
и ![]() ,
, ![]() ,
,
где а - точка в окрестности ![]() .
.
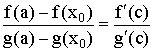 где
где ![]() .
.
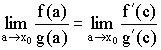
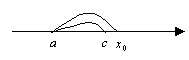
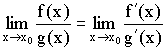
Примеры:
1) 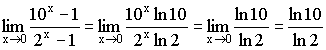
2) 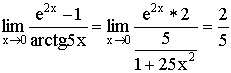
3) 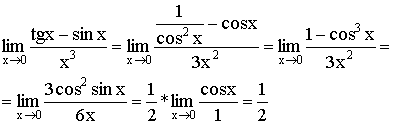
2.5. Формула Тейлора
Пусть ![]() определена и непрерывна и имеет все производные до n-ого порядка включительно, в некоторой точке
определена и непрерывна и имеет все производные до n-ого порядка включительно, в некоторой точке ![]() .
.
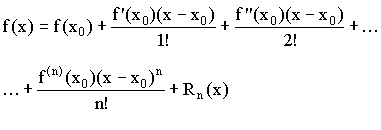
![]() - остаточный член в форме Тейлора.
- остаточный член в форме Тейлора.
![]() - полином Тейлора для
- полином Тейлора для ![]() .
.
![]()
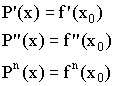
1) 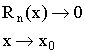
2) ![]()
3) ![]() , где k=0,1,2,…n.
, где k=0,1,2,…n.
Запись остаточного члена
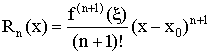
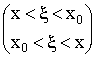 – остаточный член в форме Логранжа.
– остаточный член в форме Логранжа.
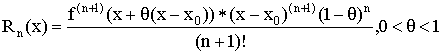 – остаточный член в форме Коши.
– остаточный член в форме Коши.
![]() – остаточный член в форме Пиано.
– остаточный член в форме Пиано.
Ряд Тейлора
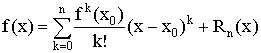
Формула Маклорена
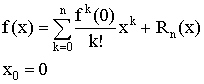
Любой многочлен совпадает со свой формулой Маклорена, при этом постоянный член равен.
1) ![]()
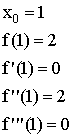
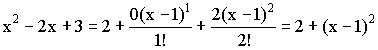
2) 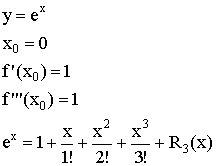
3) 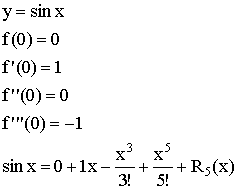
4) 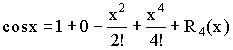
2.6. Монотонность, экстремумы функции
Функция называется возрастающей если большему значению аргумента соответствует большее значение функции, а меньшему соответствует меньше.
Функция называется убывающей если большему значению аргумента соответствует меньшее значение функции, а меньшему соответствует большее.
Теорема. У возрастающей функции производная больше 0 (![]() ).
).
Доказательство:
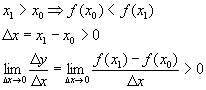
![]()
![]()
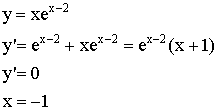
|
x |
|
-1 |
|
|
y |
min |
||
|
|
– |
0 |
+ |
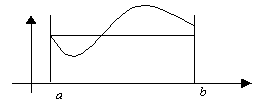
Экстремумы функции
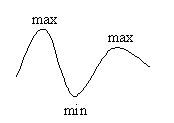 Точка
Точка ![]() -называется точкой max, если существует некоторая окрестность точки, что для любой точки x из этой окрестности
-называется точкой max, если существует некоторая окрестность точки, что для любой точки x из этой окрестности ![]() .
.
Точка ![]() -называется точкой min, если существует некоторая окрестность точки, что для любой точки x из этой окрестности
-называется точкой min, если существует некоторая окрестность точки, что для любой точки x из этой окрестности ![]() .
.
Необходимый признак экстремума, если ![]() -точка экстремума.
-точка экстремума. ![]()
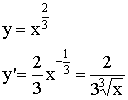
Если ![]()
![]() и
и ![]() , то это точка экстремума.
, то это точка экстремума.
Если ![]() - точка экстремума и существует
- точка экстремума и существует ![]() , то производная
, то производная ![]() =0. Точка, в которой производная, равна нулю, называется критической точкой.
=0. Точка, в которой производная, равна нулю, называется критической точкой.
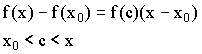 ,
,
теорема Логранжа. 
Первый достаточный признак экстремума
Если при переходе через критическую точку производная меняет знак с ”+” на “-“,то в этой точке максимум.
Если при переходе через критическую точку производная меняет знак с ”-” на “+“,то в этой точке минимум.
Второй достаточный признак экстремума
Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.
Пример:
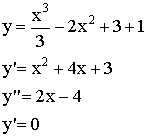
![]()
![]()
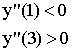
| x | 1 | 3 | |||
| y | Max | Min | |||
| + | 0 | - | 0 | + |
2.7. Выпуклость и вогнутость функции
Если в окрестности точки, график функции ниже касательной, то в окрестности этой точки график функции выпуклый.
Если в окрестности точки, график функции выше касательной, то в окрестности этой точки график функции вогнутый.
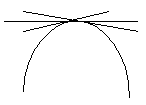
Теорема. В
точке выпуклости 2-ая производная меньше 0. В точке вогнутости вторая производная больше 0.
Доказательство:
Если прямая проходит через точку
![]()
Применим теорему Логранжа: 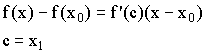
![]()
Поставим “-“ в ![]() , учитывая, что
, учитывая, что ![]() , тогда
, тогда ![]() должна быть <0.
должна быть <0.
Второй раз применим теорему Логранжа:
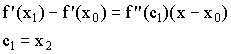
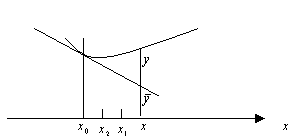
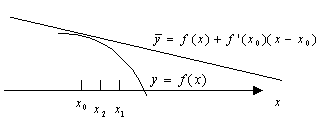
Для вогнутости поставим “+”
![]()
![]()
![]() должно быть >
должно быть >
Точка, в которой вторая производная равна нулю, называется точкой перегиба.
|
|
|
|
|
|
|
|
y |
п |
п |
|||
|
|
+ |
0 |
- |
0 |
+ |
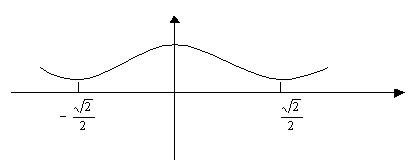
2.8. Асимптоты
Асимптотой к кривой называется прямая, к которой график функции неограниченно приближается.
Асимптоты:
- Вертикальные
- Наклонные
- Горизонтальные - (частный
случай наклонной асимптоты)
I. Вертикальные асимптоты всегда имеют уравнение ![]() , где
, где ![]() – точка разрыва второго рода.
– точка разрыва второго рода.
Значит ![]()
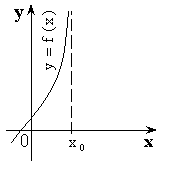
II. Наклонная асимптота имеет вид ![]() .
.
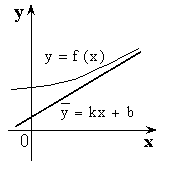
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример:
![]()
![]() – вертикальная асимптота, т.к.
– вертикальная асимптота, т.к. ![]()
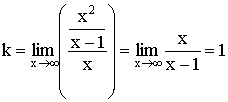
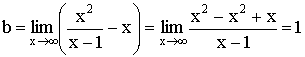
Наклонная асимптота ![]()
Возможный вариант графика функции.
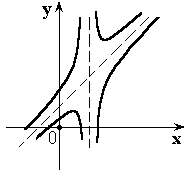
2.9. Исследование функции
План общего исследования функции.
- Область определения, четность, периодичность.
- С помощью пределов выясняем непрерывность, ищем асимптоты.
- С помощью первой производной – монотонность и экстремумы.
- С помощью второй производной – выпуклость и вогнутость, точки перегиба.
- График функции.
Примеры исследования функции
I. 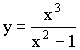
1) 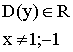 Функция нечетная.
Функция нечетная.
2) 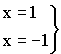 вертикальные асимптоты, т.к.
вертикальные асимптоты, т.к. 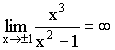
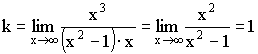
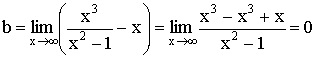
Наклонная асимптота ![]()
3) 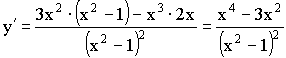
![]()
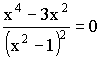
![]()
![]()
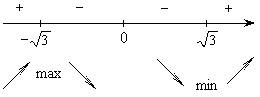
4) 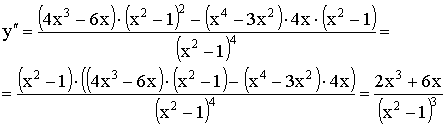
![]()
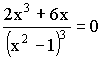
![]() – точка перегиба.
– точка перегиба.
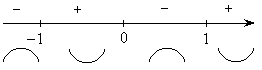
Схематичный график данной функции:
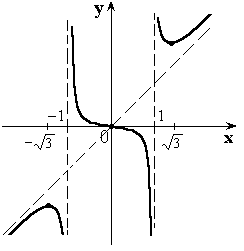
3) ![]() – функция нечетная.
– функция нечетная.
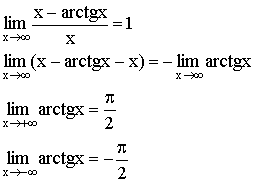
![]() - при
- при ![]()
![]() - при
- при ![]()
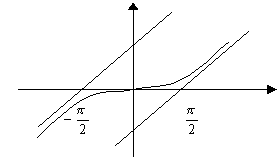
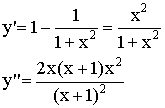
4) 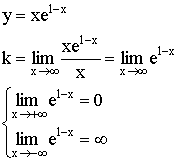 наклонных асимптот нет.
наклонных асимптот нет.
![]()
![]() - горизонтальная асимптота.
- горизонтальная асимптота.
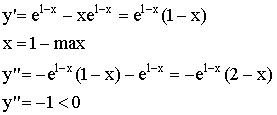
![]() - точка перегиба.
- точка перегиба.
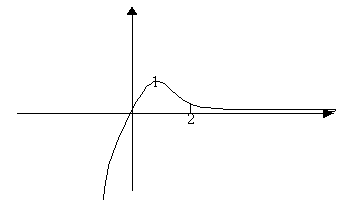
5) ![]()
![]() - вертикальная асимптота.
- вертикальная асимптота.
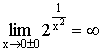
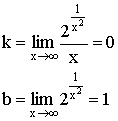
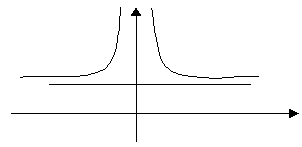
6) 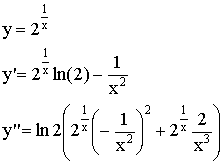
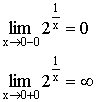
![]()
![]() -точка перегиба.
-точка перегиба.
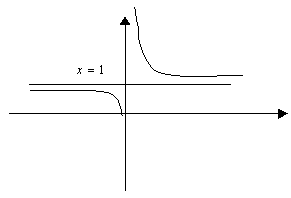
7) 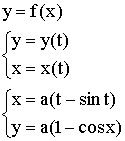
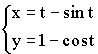
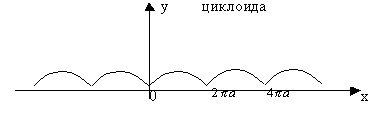
8) 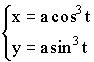
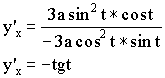
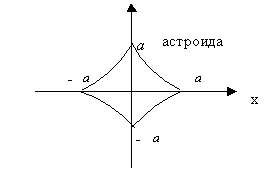
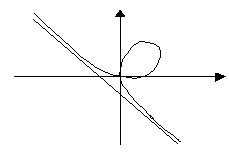
9) Декартов лист.
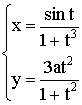
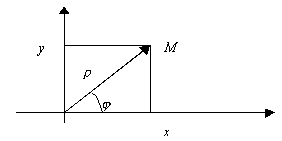
Полярные координаты
![]() – декартовы координаты.
– декартовы координаты.
![]() - полярные координаты.
- полярные координаты.
![]()
![]()
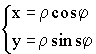
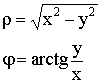
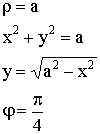
3. Интегральное исчисление
3.1. Понятие первообразной и неопределенный интеграл
Основные определения
Функция ![]() называется первообразной для функции
называется первообразной для функции ![]() , если
, если ![]() .
.
Т.1: Если ![]() и
и ![]() - первообразные для
- первообразные для ![]() , то
, то ![]()
Доказательство:
![]() ; ЧТД.
; ЧТД.
Неопределенным интегралом от ![]() называется класс всех первообразных для
называется класс всех первообразных для ![]() .
.
![]()
![]() - подынтегральная функция.
- подынтегральная функция.
![]() - дифференциал.
- дифференциал.
![]() - переменная интегрирования.
- переменная интегрирования.
Для любой непрерывной функции существует первообразная.
Основные тождества
1.![]()
2.![]()
3.![]()
3.2. Таблица интегралов
1. 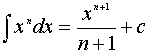
![]()
2. 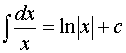
3. 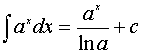
4. ![]()
5. ![]()
6. 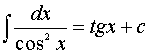
7. 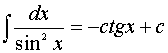
8. 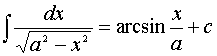
9. 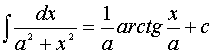
10. 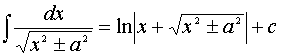
11. 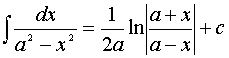
12. ![]()
13. ![]()
Доказательство каждого из табличных интегралов осуществляется с помощью дифференцирования (по определению). Например, для 10 и 11 табличных интегралов:
Доказательство:
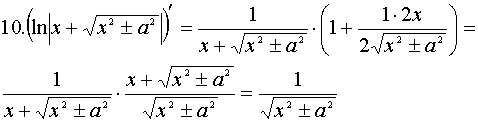
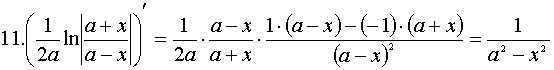
Основные свойства неопределенного интеграла
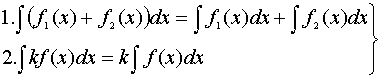 - линейность
- линейность
Следствие:
1.![]() ;
; 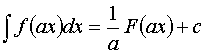
2.![]()
3.3. Основные методы интегрирования
Замена переменных под знаком неопределенного интеграла
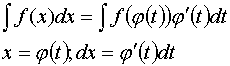
Интегрирование по частям.
![]()
Доказательство:
![]() (формула дифференцирования произведения).
(формула дифференцирования произведения).
![]() (интегрируем обе части равенства)
(интегрируем обе части равенства)
![]() (использование основного тождества)
(использование основного тождества)
![]() (что и требовалось доказать).
(что и требовалось доказать).
Пример:
1) (замена переменной)
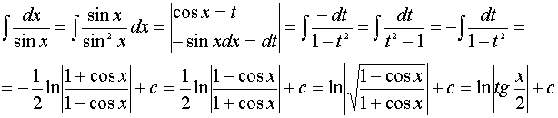
2) (интегрирование по частям)
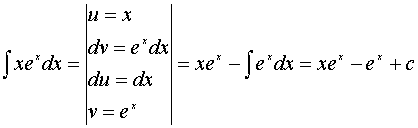
Дополнительный материал
Интегрирование рациональных дробей. Простейшие дроби и их интегрирование
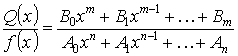
Все коэффициенты действительные числа.
m , n – целые числа.
Нет общих корней.
Если ![]() , то дробь называется неправильной, если
, то дробь называется неправильной, если ![]() , то дробь называется правильной.
, то дробь называется правильной.
Если дробь неправильная, то 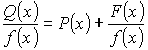 , где
, где ![]() - правильная дробь;
- правильная дробь; ![]() - многочлен.
- многочлен.
Простейшие дроби:
1.![]()
2.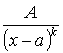 ,
, ![]() и целое число.
и целое число.
3.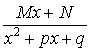 ( в знаменателе неприводимый квадратный трехчлен).
( в знаменателе неприводимый квадратный трехчлен).
4.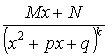 ,
, ![]() и целое число.
и целое число.
![]()
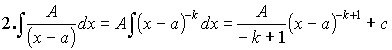
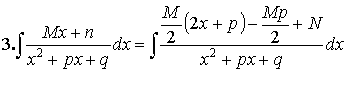 =
=
=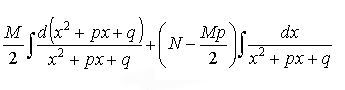 =
=
=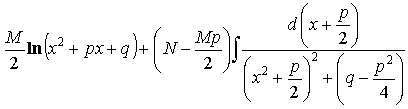 =
=
=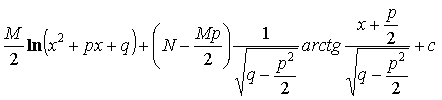
Разложить рациональные дроби на простейшие
Теорема. Если х = а – корень знаменателя f(x) кратности k , то
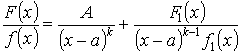
Доказательство:
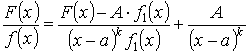 ; (1)
; (1)
Будем подбирать А так, чтобы ![]() По теореме Безу это возможно, если
По теореме Безу это возможно, если
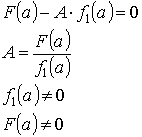
Тогда ![]()
Подставим в (1) 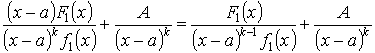
Следствие:
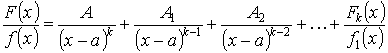
Теорема. Если ![]() (
(![]() - неприводимый квадратный трехчлен.
- неприводимый квадратный трехчлен. ![]() ), то
), то
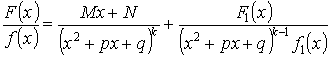
Доказательство:
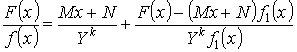
Подберем M и N так, чтобы числитель делился на Y :
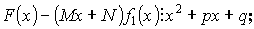
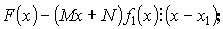
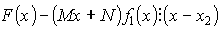
![]() - по теореме Безу.
- по теореме Безу.
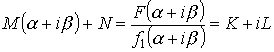
![]()
M и N можно найти из этой системы всегда.
Следствие: всякая правильная рациональная дробь может быть разложена в сумму простейших дробей.
![]()
Пример:
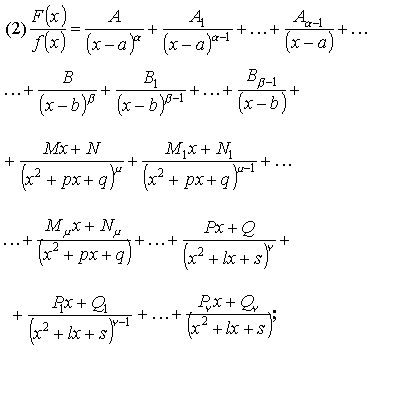
Метод неопределенных коэффициентов
Правую часть равенства (2) надо привести к общему знаменателю и приравнять в числители коэффициенты при одинаковых степенях F(x). Решая полученную систему уравнений можно определить все коэффициенты.
Интегрирование рациональных дробей
- Выделить целую часть дроби.
- Разложить знаменатель на множители.
- Представить в виде суммы простейших дробей.
- Найти неопределенные коэффициенты.
- Интегрировать каждую простейшую дробь.
Интегрирование иррациональных функций
3.3.1. 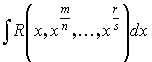
k – общий знаменатель дробей ![]()
![]() - рационализирующая подстановка.
- рационализирующая подстановка.
Пример:
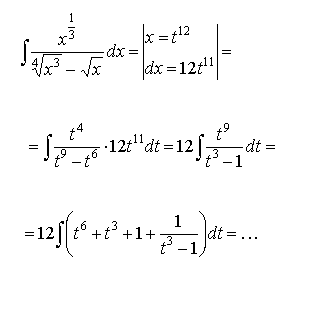
3.3.2. 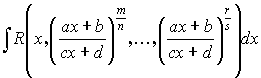
k – общий знаменатель дробей ![]()
![]()
Пример:
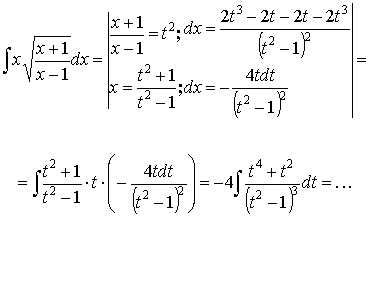
3.3.3. Тригонометрические подстановки.
![]()
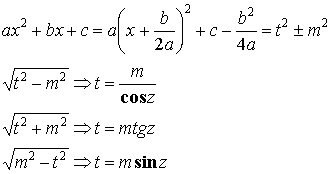
Пример:
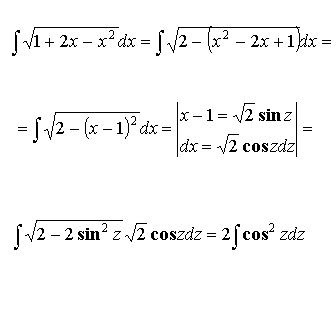
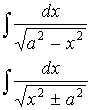 - обратные гиперболические функции.
- обратные гиперболические функции.
![]()
![]()
![]()
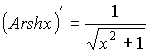
![]()
![]()
![]()
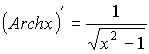
![]()
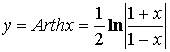
![]()
![]()
![]()
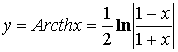
![]()
![]()
3.4. Понятие определенного интеграла и его вычисление
Определение и свойства
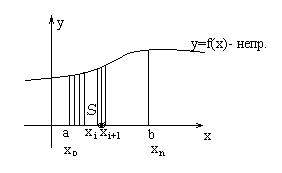
S – область – криволинейная трапеция.
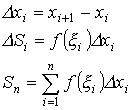
Интегральная сумма: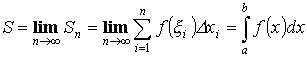
![]()
Определенным интегралом называется предел интегральной суммы.
Теорема. “О существовании определенного интеграла”
Если f(x) – непрерывна на отрезке (a,b), то определенный интеграл существует и не зависит от порядка разбиения и выбора точек.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Свойства определенного интеграла:
-
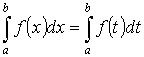
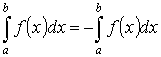
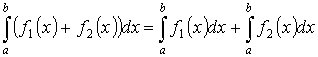
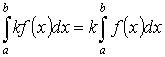
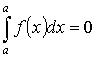
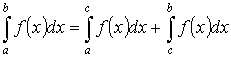 - аддитивность.
- аддитивность.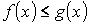 на
на 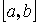
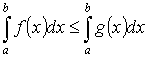
Основные теоремы интегрального исчисления
Теорема 1. “об оценке”
Пусть y =f(x) интегрируема на [a ,b] ![]() Тогда
Тогда 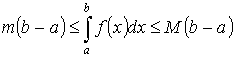
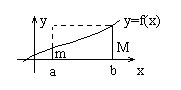
Доказательство:
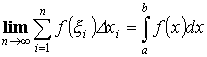
![]()
![]()
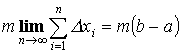
![]()
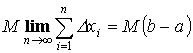
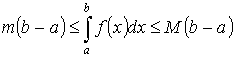
Теорема 2. “о среднем”
Пусть y =f(x) интегрируема на [a ,b] Тогда 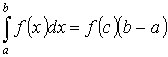 - где
- где ![]() f(c) – среднее значение f(x) на [a ,b].
f(c) – среднее значение f(x) на [a ,b].
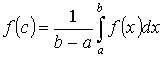
Доказательство:
По Т.1: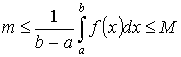
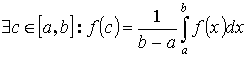
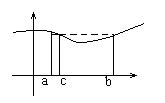
Т.к. f(x) – непрерывна на [a ,b], то она принимает все промежуточные значения от m до M. Следовательно она принимает значение
А. Т.е. существует такая 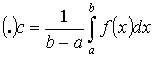
Теорема 3. “о производной определенного интеграла по переменному верхнему пределу”
Пусть y =f(x) - интегрируема на [a , b]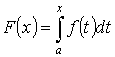
![]() . Тогда
. Тогда ![]()
Доказательство:
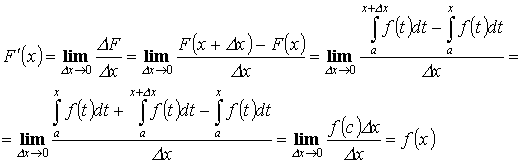
![]()
Теорема 4. “формула Ньютона-Лейбница”
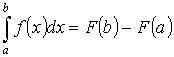 , где F(x) – первообразная для f(x).
, где F(x) – первообразная для f(x).
Доказательство:
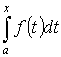 - первообразная для f(x) по Т.3. Т.к. первообразные отличаются на const, то
- первообразная для f(x) по Т.3. Т.к. первообразные отличаются на const, то 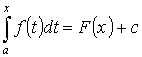 Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b
Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b 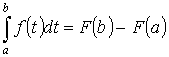
Методы вычисления определенного интеграла
Замена переменных под знаком определенного интеграла.
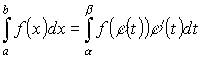
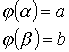
Пример:
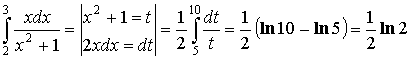
Интегрирование по частям в определенном интеграле.
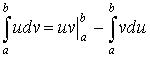
Пример:
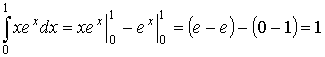
3.5. Приложения определенного интеграла
Площадь плоской фигуры (в декартовой системе координат)
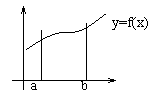
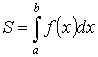 - из определения
- из определения
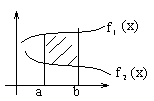

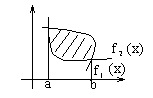
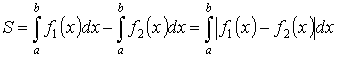
![]()
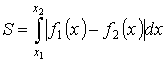
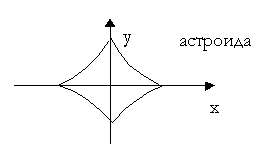
Площадь плоской фигуры (параметрическое задание)
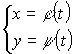
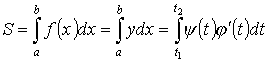
Пример:
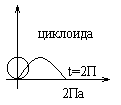
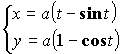
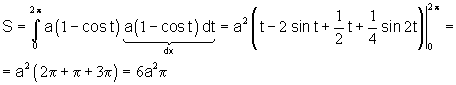
Площадь плоской фигуры (в полярной системе координат)
![]()
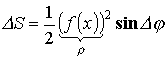 .
. 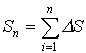 .
. 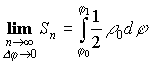 .
. 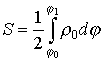 .
.
Пример:
![]()
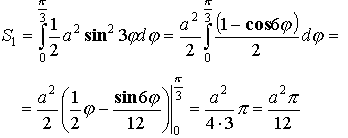
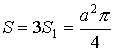
Примеры решения задач
Задача 1.
Теоретическое введение
Функцией переменной величины ![]() , называется величина
, называется величина ![]() такая, что каждому значению
такая, что каждому значению ![]() , принадлежащей некоторой области
, принадлежащей некоторой области ![]() , соответствует единственное значение величины
, соответствует единственное значение величины ![]() .
.
Обозначение: ![]() .
.
![]() – область определения функции,
– область определения функции, ![]() – аргумент.
– аргумент.
![]() – область изменения функции,
– область изменения функции, ![]() – значение;
– значение;
Функция может быть задана аналитически, таблично, графически.
Основными элементарными функциями являются:
-
- степенные (
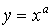 , где
, где  – произвольное число)
– произвольное число)
- степенные (
- показательные (
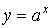 ,
, 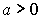 ,
,  )
) - логарифмические (
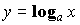 ,
,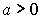 ,
,  )
) - тригонометрические
(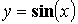 ,
, 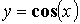 ,
, 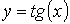 ,
, 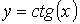 )
) - обратные тригонометрические
(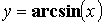 ,
,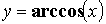 ,
,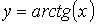 ,
, 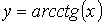 )
)
Композиция (суперпозиция) двух функций ![]() и
и ![]() есть функция, в которой аргументом одной из данных функции, является значение другой функции.
есть функция, в которой аргументом одной из данных функции, является значение другой функции.
Обозначение: ![]() и
и ![]() .
.
Сложная функция есть композиция двух и более функций.
Элементарная функция есть функция, полученная из основных элементарных функций с помощью арифметических действии и композиции.
Целью математического анализа является изучение различных функций, их свойств, и операций связанных с функциями.
Функция называется четной, если ![]() для всех своих аргументов.
для всех своих аргументов.
Функция называется нечетной, если ![]() для всех своих аргументов.
для всех своих аргументов.
Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , стремящемся к
, стремящемся к ![]() и обознается
и обознается ![]() , если при неограниченном приближении
, если при неограниченном приближении ![]() к
к ![]() ,
, ![]() неограниченно приближается
неограниченно приближается ![]() .
.
Свойства пределов:
- Передел суммы двух функций равен сумме пределов этих функций, если они существуют:
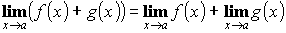
- Предел произведения функции равен произведению пределов, если они существуют:
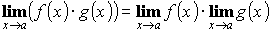
- Предел частного двух функций равен частному пределов, если они существуют, и предел знаменателя не равен нулю:
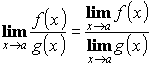 , при
, при 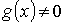 .
.
Обычно ![]() , например:
, например:
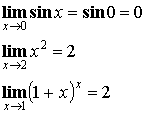
Однако, иногда значение ![]() не входит в область определения функции
не входит в область определения функции ![]() .
.
В этом случае имеются различные методы вычисления пределов:
Выделение общего множителя
Выделение главной части
Использование замечательных пределов
Первый замечательный предел: ![]()
Второй замечательный предел: 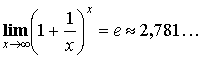
Задача 2.
Теоретическое введение
Производная ![]() или
или ![]() от данной функции
от данной функции ![]() есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:
есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю: ![]() или
или ![]()
Механический смысл производной – скорость изменения функции.
Геометрический смысл производной – тангенс угла наклона касательной к графику функции:
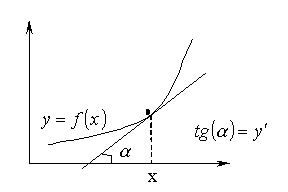
Правила дифференцирования:
- Производная постоянной величины равна 0.
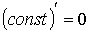
- Производная суммы равна сумме производных.
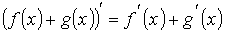
- Производная произведения:

- Производная частного:
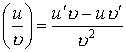
Производная сложной функции:
Производная от сложной функции ![]() по независимому аргументу
по независимому аргументу ![]() равна производной от
равна производной от ![]() по промежуточному аргументу
по промежуточному аргументу ![]() , умноженной на его производною по независимой переменной
, умноженной на его производною по независимой переменной ![]() .
.
![]()
Примеры:
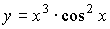 ;
; 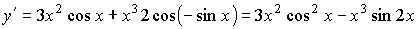
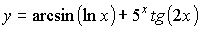 ;
; 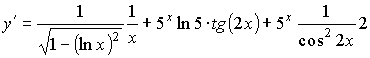
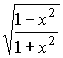 ;
; 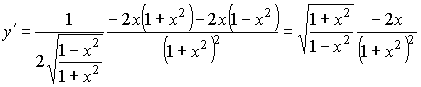
Задача 4.
Найти неопределенные интегралы:
а)![]() ;
;
Решение: введем переменную ![]() . Тогда
. Тогда ![]() ;
; 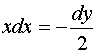 . Сделаем замену:
. Сделаем замену:
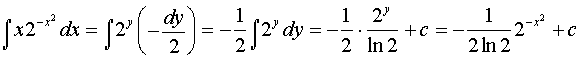 .
.
б) ![]() ;
;
Решение: используем метод интегрирования по частям:
![]() .
.
Обозначим: ![]() .
.
Тогда 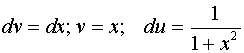 .
.
Задача 5.
Вычислить площадь фигуры, ограниченной линиями:
![]() и
и ![]() .
.
Решение:
Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение ![]()
![]()
Итак, точки пересечения ![]() и
и ![]() .
.
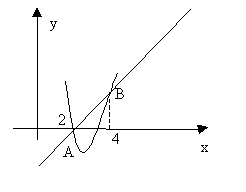
Площадь фигуры найдем, используя формулу
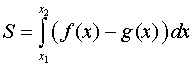 .
.
В нашем случае
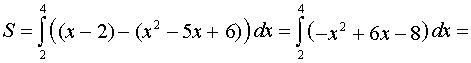
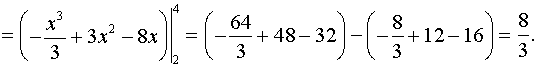
Ответ: площадь равна ![]() (квадратных единиц).
(квадратных единиц).