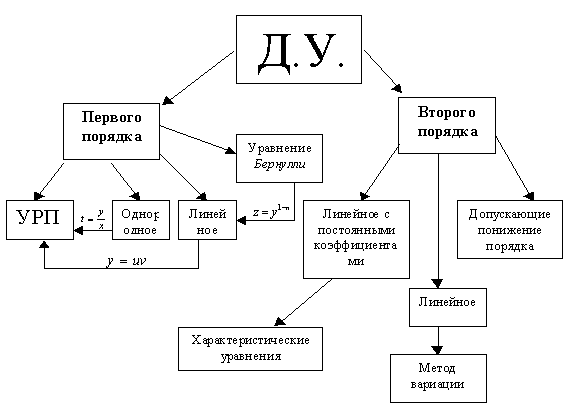
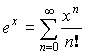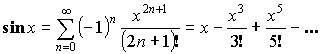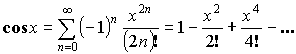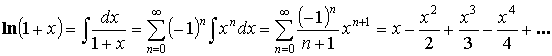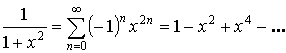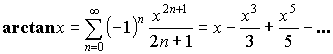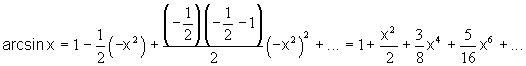10. Дифференциальные уравнения
10.1. Понятие о дифференциальном уравнении. Общее и частное решение уравнения. Задача Коши
8. Кратные интегралы
8.1. Двойной интеграл
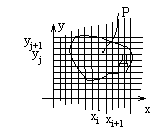
Пусть функция двух переменных z=f(x,y) – непрерывна на Д, где Д={(x,y)} – замкнутая область.
Разобьем эту область на прямоугольные части, как показано на рисунке.
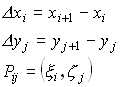
Вычислим объем параллелепипеда с основанием 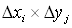 и высотой
и высотой 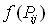 :
:
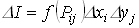 - элементарный объем параллелепипеда.
- элементарный объем параллелепипеда.
Тогда двойным интегралом от функции f(x,y) по области Д называется предел интегральной суммы (суммарного объёма)
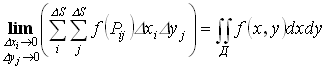 ,
,
если этот предел существует.
Теорема о существовании двойного интеграла
Если функция от x, y непрерывна в замкнутой области Д, то двойной интеграл существует и не зависит от способов разбиения и выбора точки в каждой элементарной области.
Геометрический смысл двойного интеграла – объем цилиндра, ограниченного снизу областью Д на плоскости (x, y), сверху поверхностью z = f(x, y).
Свойства двойного интеграла:
1)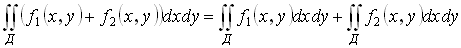
2)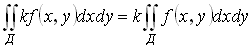
3)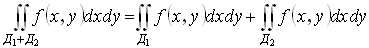
Вычисление двойного интеграла:
Пусть Д – правильная область, т.е. любая прямая, параллельная осям координат пересекает область не более, чем в двух точках
Пусть (соответственно рисунку) уравнения верхней и нижней граничных линий есть 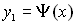 и
и 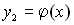 .
.
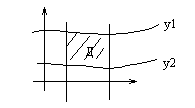 Тогда двойной интеграл можно представить в виде повторного интеграла
Тогда двойной интеграл можно представить в виде повторного интеграла
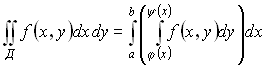 .
.
Пример:
F(x, y)=x+ y
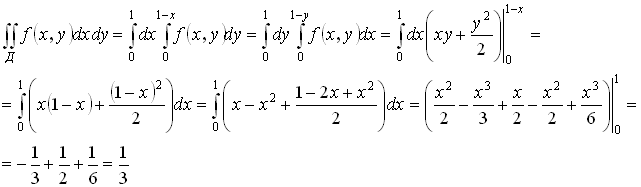
Для вычисления двойного интеграла формируется повторный интеграл (порядок интегрирования выбирается самостоятельно). Заметим, что пределы внутреннего интеграла могут зависеть только от внешней переменной.
Теорема об оценке двойного интеграла:
Пусть 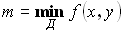 и
и 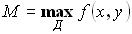 . Тогда
. Тогда
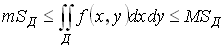 .
.
Следствие: площадь области Д равна 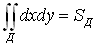
Пример:
Пусть область Д ограничена линиями: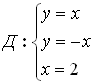
Интегрируемая функция 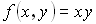 . Тогда
. Тогда
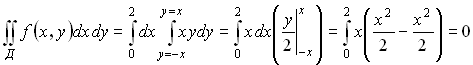 .
.
8.2. Двойной интеграл в полярной системе координат
Формулы перехода от декартовой в полярную систему координат:
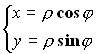 .
.
Тогда 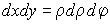 . Двойной интеграл принимает вид:
. Двойной интеграл принимает вид:
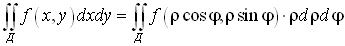
8.3. Тройной интеграл
Пусть функция трёх переменных u=f(x,y,z) непрерывна в V , где V – замкнутая, ограниченная область в пространстве.
Разобьем область V на части плоскостями, параллельными координатным плоскостям. В каждом полученном параллелепипеде выберем точку 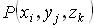 и вычислим значение функции в этой точке
и вычислим значение функции в этой точке 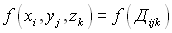 . Составим интегральную сумму
. Составим интегральную сумму 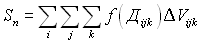 , где
, где 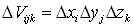 .
.
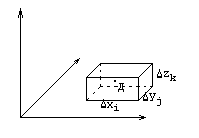
Переходя к пределу (если он существует), получим тройной интеграл:
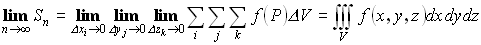 .
.
Если функция непрерывна в замкнутой, ограниченной области, то тройной интеграл существует и не зависит от способа разбиения и выбора точки.
Свойства тройного интеграла:
1. Линейность
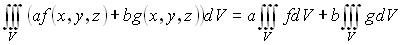
2. Аддитивность
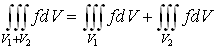 . Здесь
. Здесь 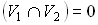 .
.
3. Если 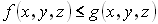
на V
то 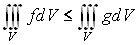
Вычисление тройного интеграла:
Пусть V – прямоугольный параллелепипед.
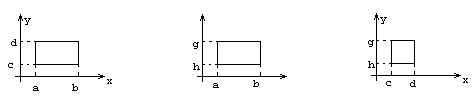
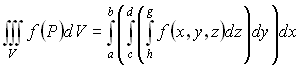 - трехкратный повторный интеграл.
- трехкратный повторный интеграл.
Пример:
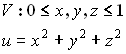
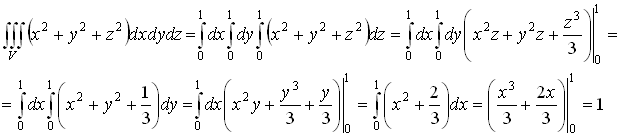
Пример:
V – произвольное тело (правильное)
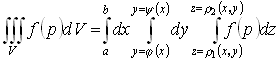
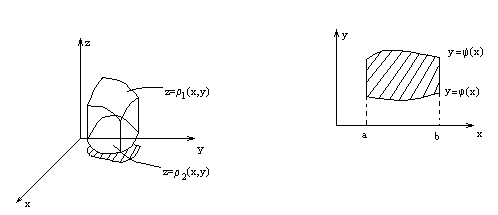
Вычисление тройного интеграла по произвольной области сводится к вычислению трехкратного повторного интеграла, причем внутренний интеграл берется между двумя ограничивающими поверхностями, средний – между двумя ограничивающими линиями, внешний – между двумя числами. Пределы интегрирования повторного интеграла не должны зависеть от внутренних переменных.
Пример:
u=f(x,y,z)
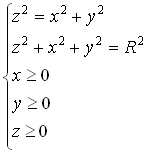
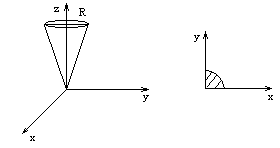
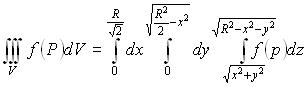
В этом примере удобно перейти в цилиндрическую систему координат.
9. Ряды
9.1. Числовые ряды
Сходимость ряда. Сумма ряда
Пусть даны ![]() , тогда
, тогда 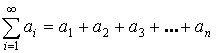 – ряд, где
– ряд, где ![]() – член ряда.
– член ряда.
Примеры различных рядов:
- 1+2+4+…+
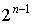 – ряд сходится.
– ряд сходится. - 1–1+1–1+…+
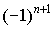 – расходится.
– расходится.
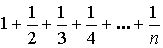 – расходится (гармонический ряд).
– расходится (гармонический ряд).
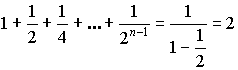 - сходится.
- сходится.
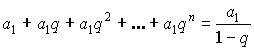 , при
, при ![]() .
.
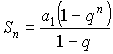
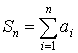 – частичная сумма
– частичная сумма
Если ![]() , то
, то ![]() – сумма ряда. Ряд сходится, если этот предел существует, и расходится, если не существует.
– сумма ряда. Ряд сходится, если этот предел существует, и расходится, если не существует.
Пример:
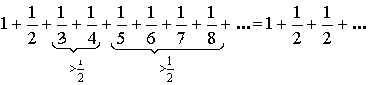
![]()
Теорема. О сходимости ряда
Сходимость ряда не измениться, если отбросить конечное число его членов.
Признаки сходимости ряда
- Необходимый признак сходимости:
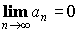
- Достаточный признак расходимости:
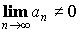
Доказательство:
![]()
![]()
![]()
Если ![]() , то ряд сходится.
, то ряд сходится.
-
- Достаточный признак сходимости (для знакопостоянных рядов):
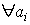
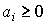
- Признак сравнения:
- Достаточный признак сходимости (для знакопостоянных рядов):
Имеем ![]() и
и ![]() , то
, то
![]()
![]() и
и ![]() – сходится, тогда
– сходится, тогда ![]() – сходится.
– сходится.
![]() или
или ![]() .
.
Если 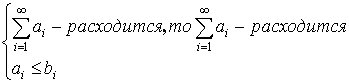
Пример:
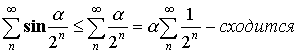 , а значит
, а значит 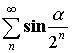 – сходится.
– сходится.
-
- Признак Даламбера:
Пусть 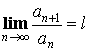 , тогда при
, тогда при
![]() – ряд сходится,
– ряд сходится, ![]() – ряд расходится,
– ряд расходится, ![]() – требуются дальнейшие исследования.
– требуются дальнейшие исследования.
Доказательство:
Пусть ![]() , тогда
, тогда ![]() , начиная с некоторого
, начиная с некоторого ![]() .
.
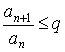
![]() или
или ![]()
Получаем 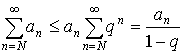
Пример:
Ряд – ![]()
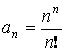 и
и 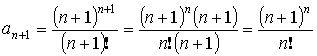
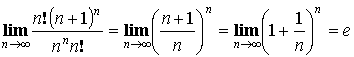 – ряд расходится.
– ряд расходится.
- Радикальный признак Коши:
![]() , при
, при ![]() ,
, ![]() .
.
Тогда если ![]() , то ряд сходится, если
, то ряд сходится, если ![]() – ряд расходится.
– ряд расходится.
Доказательство:
-
- Пусть
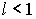 и
и 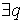
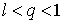
- Пусть
Тогда, начиная с некоторого ![]() ,
, ![]() , выполняется неравенство
, выполняется неравенство ![]() или
или ![]() .
.
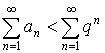
![]() – сходится (бесконечно убывающая геометрическая прогрессия), а значит
– сходится (бесконечно убывающая геометрическая прогрессия), а значит ![]() –сходится по принципу сравнения.
–сходится по принципу сравнения.
- Пусть
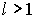 и
и 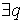
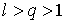
Тогда, начиная с некоторого ![]() ,
, ![]() , выполняется неравенство
, выполняется неравенство ![]() или
или ![]() .
.
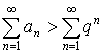
Получаем, что ![]() –расходится.
–расходится.
Пример:
Ряд – ![]() .
.
Получаем 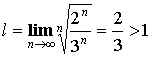 – ряд сходится.
– ряд сходится.
- Интегральный признак Коши:
![]() , при
, при ![]() .
.
![]()
![]()
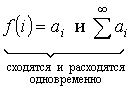
Доказательство:
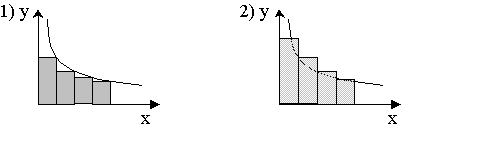
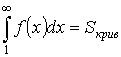 и
и 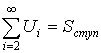
![]()
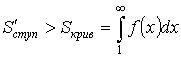
Значит, если ![]() – сходится
– сходится 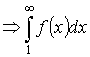 – сходится.
– сходится.
Знакочередующиеся ряды
Ряды вида: ![]() , где
, где ![]() .
.
Теорема Лейбница
Если ![]() и
и ![]() , то ряд
, то ряд 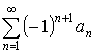 – сходится.
– сходится.
Доказательство:
Пусть ![]() , тогда
, тогда
![]() . При
. При ![]()
![]() .
. ![]() ограниченна сверху
ограниченна сверху ![]() .
.
Так как ![]() – возрастает и ограниченна сверху
– возрастает и ограниченна сверху ![]()
Пример: ![]() – сходится.
– сходится.
Пусть дан ряд ![]() , тогда
, тогда
-
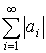 – сходится, тогда ряд – абсолютно сходится.
– сходится, тогда ряд – абсолютно сходится.
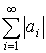 – расходится и
– расходится и 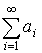 – сходится, тогда ряд сходится условно.
– сходится, тогда ряд сходится условно.
Теорема. Если ряд абсолютно сходится, то любая перестановка членов не меняет сумму.
Если ряд сходится условно, то подходящей перестановкой можно сделать его сумму равной любому числу и даже сделать его расходящимся.
Действия над рядами
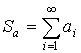 ,
, 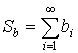 – абсолютно сходящиеся.
– абсолютно сходящиеся.
Тогда 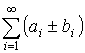 – абсолютно сходится.
– абсолютно сходится.
Функциональные ряды
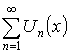 , где
, где ![]() – функция.
– функция.
Область сходимости
Пусть ![]() фиксировано.
фиксировано.
Тогда 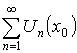 сходится, если
сходится, если ![]() –точка сходимости, и расходится, если
–точка сходимости, и расходится, если ![]() – точка расходимости.
– точка расходимости.
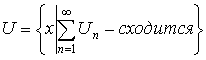 – область сходимости.
– область сходимости.
Пример:
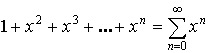
![]() , то ряд сходится.
, то ряд сходится.
![]()
![]() , где
, где ![]() – остаток ряда.
– остаток ряда.
Если ряд сходится, то ![]()
Мажорируемые ряды
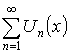 , где
, где ![]() – мажорируемы.
– мажорируемы.
Тогда ![]() – мажоранжа (если ряд сходится), при
– мажоранжа (если ряд сходится), при ![]() .
.
Теорема. О непрерывности суммы ряда
Пусть 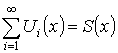 .
.
![]()
![]() – сходится и
– сходится и ![]() ,
, ![]() – непрерывна на
– непрерывна на ![]() .
.
Тогда ![]() – непрерывна на
– непрерывна на ![]() .
.
Доказательство:
![]() (из определения непрерывности)
(из определения непрерывности)
![]() ,
,
где ![]() .
.
При ![]() и
и ![]() .
.
Отсюда ![]()
Пример:
![]() на
на ![]()
![]()
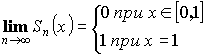 , разрыв при
, разрыв при ![]()
Теорема. О почленном интегрировании ряда
Пусть 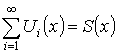 на
на ![]() – мажорируемый,
– мажорируемый, ![]() – интегрируемы на
– интегрируемы на ![]() (
(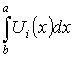 – существует). Тогда
– существует). Тогда 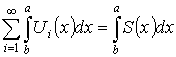
Теорема. О почленном дифференцировании ряда
Пусть 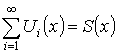 на
на ![]() – мажорируемый,
– мажорируемый, ![]() – дифференцируемы на
– дифференцируемы на ![]() (
(![]() – существует). Тогда
– существует). Тогда 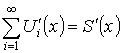
9.2. Степенные ряды
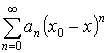 , где
, где ![]() – коэффициент,
– коэффициент, ![]() – произвольная точка,
– произвольная точка, ![]() .
.
Частный случай: 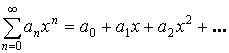
Теорема Абеля: У каждого степенного ряда существует радиус сходимости.
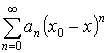 , при
, при
![]() – сходится
– сходится
![]() – расходится.
– расходится.
![]() – точка сходимости.
– точка сходимости.
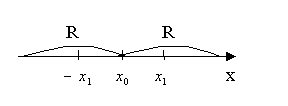
Если ![]() , то
, то ![]() , т.е.
, т.е. ![]() – мажорируемый.
– мажорируемый.
Область сходимости: ![]()
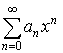 – сходится при
– сходится при ![]()
Пример:
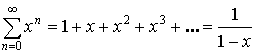 – сходится при
– сходится при ![]() .
.
Теорема. Радиус сходимости ![]() определяется как
определяется как 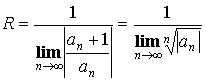 .
.
Доказательство:
Возьмем ![]() , тогда
, тогда 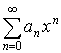
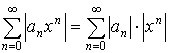
По признаку Даламбера:
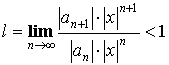
Отсюда 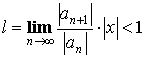 или
или 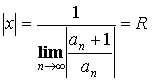
Внутри радиуса сходимости степенной ряд мажорируем, его сумма непрерывна, его можно почленно интегрировать и дифференцировать.
Пример:
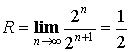 или при
или при ![]() ряд сходится.
ряд сходится.
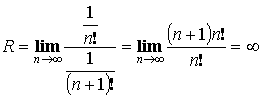 , значит ряд сходится при любых
, значит ряд сходится при любых ![]()
![]() , значит при
, значит при ![]() ряд сходится.
ряд сходится.
Разложение функций в степенной ряд
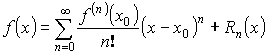 – ряд Тейлора.
– ряд Тейлора.
![]() , тогда
, тогда 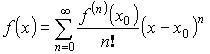
При ![]()
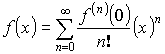 – ряд Маклорена.
– ряд Маклорена.
Разложение некоторых функций в степенной ряд
![]() или
или ![]() – любое.
– любое.
![]() или
или ![]() – любое.
– любое.
![]() или
или ![]() – любое.
– любое.
-
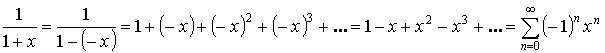
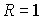 или при
или при 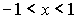 ряд сходится
ряд сходится
![]() или при
или при ![]() ряд сходится
ряд сходится
Сумма знакочередующегося ряда имеет погрешность не превосходящую первого отброшенного члена.
![]()
![]()
Пример:
![]()
Имеем
![]()
![]()
![]()
Получаем
![]()
![]()
Считая, что 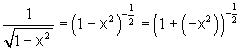
Пример:
![]()
Контрольные примеры:
-
- Разложим в ряд
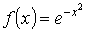 и посчитаем
и посчитаем 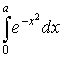
- Разложим в ряд
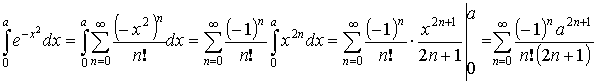
- Разложим в ряд
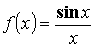 и посчитаем
и посчитаем 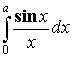
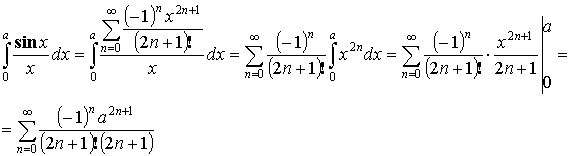
Пример разложения функции в ряд Маклорена:
![]()
![]()
![]()
![]()
![]()
Получаем ![]()
10. Дифференциальные уравнения
10.1. Понятие о дифференциальном уравнении. Общее и частное решение уравнения. Задача Коши
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и её производные.
Общий вид ![]() ,
,
где n - порядок старшей производной, который определяет порядок дифференциального уравнения.
Решением дифференциального уравнения является всякая функция, которое превращает уравнение в тождество.
Примеры:
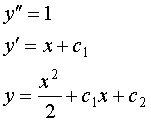
Общее решение - это решение, зависящее от произвольных констант или совокупность всех частных решений. Частное решение - это решение при фиксированном значении произвольных констант. Общий интеграл дифференциального уравнения:
![]()
Пример:
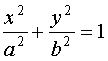
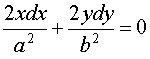
![]() - дифференциальное уравнение в дифференциалах.
- дифференциальное уравнение в дифференциалах.
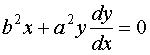 или
или ![]()
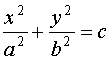 - общий интеграл.
- общий интеграл.
Задача Коши. Начальные условия: ![]() и
и ![]()
Частное решение дифференциального уравнения должно удовлетворять и тому и другому условию.
10.2. Дифференциальные уравнения первого порядка
![]()
![]() – уравнение, разрешенное относительно производной.
– уравнение, разрешенное относительно производной.
Теорема. О существовании и единственности решения (Теорема Ковалевской).
Пусть ![]() непрерывна в открытой области Д и
непрерывна в открытой области Д и ![]() .
.
Открытая область – это область без своей границы.
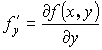 – существует и непрерывна в Д, гладкая по
– существует и непрерывна в Д, гладкая по ![]() .
.
Пусть ![]()
Тогда имеется решение ![]() такое, что
такое, что ![]() , и это решение единственное.
, и это решение единственное.
УРП (Дифференциальные уравнения 1-ого порядка с разделяющимися переменными).
![]() - УРП, если
- УРП, если ![]() .
.
![]()
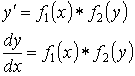
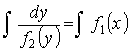 - разделение переменных
- разделение переменных
![]() - общее решение данного дифференциального уравнения.
- общее решение данного дифференциального уравнения.
Пример:
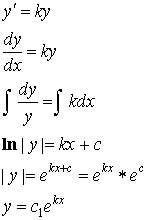
Однородное уравнение 1-ого порядка.
![]() - называется однородным если функция
- называется однородным если функция ![]() , является однородной функцией, нулевого измерения.
, является однородной функцией, нулевого измерения.
![]() - однородная функция n-ого измерения если
- однородная функция n-ого измерения если ![]()
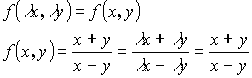 (0-е измерение)
(0-е измерение)
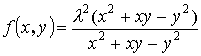
![]() (2-ого порядка)
(2-ого порядка)
![]() (неоднородная)
(неоднородная)
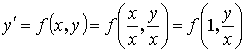
Введем новую функцию:
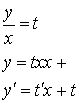
Уравнение примет вид:![]()
![]() - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными
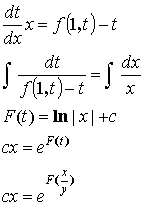
Пример:
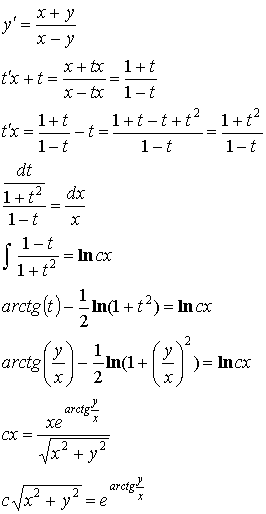
![]()
Линейные уравнение 1-ого порядка и их решение
Уравнение называется линейным, если его можно записать в следующем виде: ![]() , где
, где ![]() и
и ![]() - произвольные функции от
- произвольные функции от ![]() .
.
![]() - линейное уравнение без правой части.
- линейное уравнение без правой части.
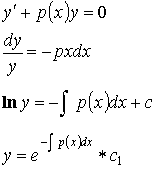
![]()
![]()
![]()
Два метода решения линейных уравнений:
- Метод Бернулли
- Метод Лагранжа (вариации произвольной постоянной)
-
- Метод Бернулли: замена неизвестной функции y(x) на произведение двух неизвестных функций
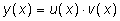
- Метод Бернулли: замена неизвестной функции y(x) на произведение двух неизвестных функций
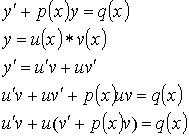
Выберем ![]() так, чтобы
так, чтобы ![]() .
.
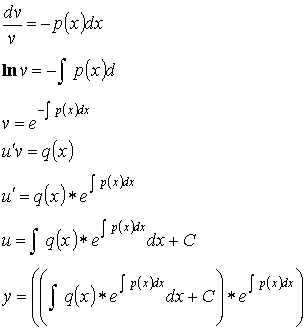
- Метод Лагранжа:
![]()
![]() - уравнение без правой части.
- уравнение без правой части.
![]() (2)
(2)
![]() - удовлетворяет уравнению (2).
- удовлетворяет уравнению (2).
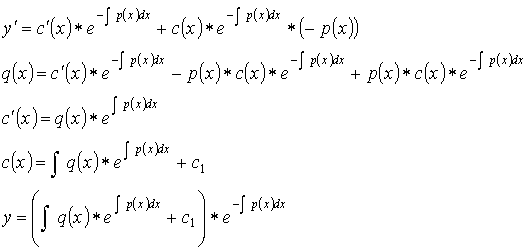
Пример:
![]()
1)
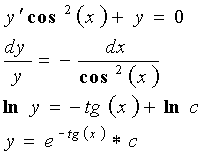
2)
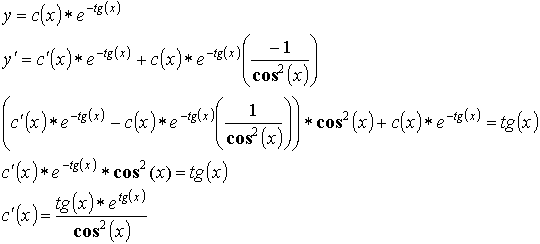
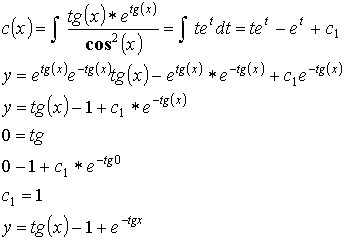
10.3. Дифференциальные уравнения второго порядка
Линейное дифференциальное уравнения 2-ого порядка с постоянными коэффициентами.
![]() (****),
(****), ![]()
![]() и
и ![]() - константы – неоднородное или с правой частью.
- константы – неоднородное или с правой частью.
![]() (***) - однородное или без правой части.
(***) - однородное или без правой части.
![]() - общее решение уравнения (****), где
- общее решение уравнения (****), где ![]() - общее решение соответствующего однородного уравнения (***),.где
- общее решение соответствующего однородного уравнения (***),.где ![]() и
и ![]() - произвольные постоянные, а
- произвольные постоянные, а ![]() и
и ![]() - линейно независимые решения (***).
- линейно независимые решения (***).
![]() - какое-либо частное решение уравнение (****).
- какое-либо частное решение уравнение (****).
Решение линейных дифференциальных уравнений 2-ого порядка с постоянными коэффициентами без правой части.
Будем искать ![]() и
и ![]() в виде
в виде ![]() .
.
Подставим ![]() в уравнение (***).
в уравнение (***).
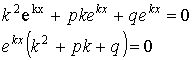
![]() - характеристическое уравнение для уравнения (***).
- характеристическое уравнение для уравнения (***).
Случай 1) ![]()
![]() и
и ![]() - действительные различные корни.
- действительные различные корни.
![]()
![]()
![]()
Случай 2) ![]()
![]() , где
, где ![]() - корень уравнения кратности 2.
- корень уравнения кратности 2.
![]()
Подставим ![]() в уравнение (***).
в уравнение (***).
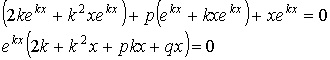
![]()
![]() , так как
, так как ![]() - это корень.
- это корень.
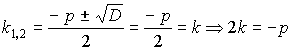
![]()
Случай 3) ![]()
![]() , где
, где ![]() -мнимая единица
-мнимая единица ![]() .
.
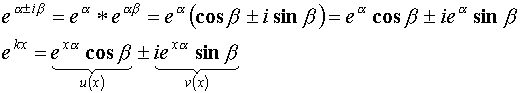
Подставим в уравнение (***).
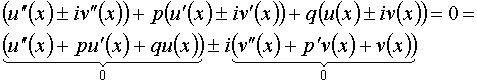
![]() - линейно независимые, следовательно:
- линейно независимые, следовательно:
![]()
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
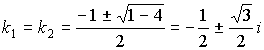
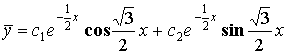
![]()
![]()
![]()
![]()
![]()
Решение линейных дифференциальных уравнений 2-ого порядка с постоянными коэффициентами с правой частью.
![]()
![]()
![]() - ищется в таком же виде, в котором задана правая часть.
- ищется в таком же виде, в котором задана правая часть.
а)
![]()
![]() ,где А - неопределенный коэффициент.
,где А - неопределенный коэффициент.
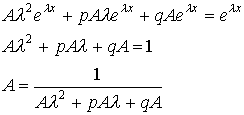
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
б) ![]()
![]()
![]()
![]()
![]()
![]()
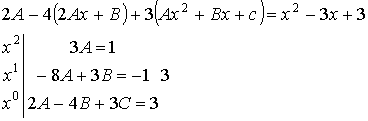
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Общий случай ![]()
![]() - характеристическое уравнение.
- характеристическое уравнение.
а) Если ![]() не корень характеристического уравнения:
не корень характеристического уравнения:
![]()
б) Если ![]() корень характеристического уравнения кратности
корень характеристического уравнения кратности ![]()
![]()
![]()
|
|
|||||
|
1 |
2 |
|
2 |
0 |
|
|
1 |
2 |
|
0 |
-1 |
|
|
1 |
2 |
|
1 |
-1 |
|
|
1 |
2 |
|
0 |
i |
|
|
1 |
2 |
|
1 |
i |
|
|
1 |
2 |
|
0 |
1 |
|
|
1 |
2 |
|
2 |
1 |
|
|
1 |
2 |
|
0 |
1+i |
|
|
0 |
1 |
|
2 |
0 |
|
|
2 |
2 |
|
0 |
2 |
|
|
2 |
2 |
|
1 |
2 |
|
|
i |
-i |
|
0 |
i |
|
|
2+i |
2-i |
|
0 |
2 |
|
|
2+i |
2-i |
|
0 |
2+i |
|
Теорема. Если ![]() , то
, то ![]() , где
, где ![]() отвечает за
отвечает за
![]() , а
, а ![]() отвечает за
отвечает за ![]() .
. ![]() - частное решение уравнения
- частное решение уравнения ![]() , а
, а ![]()
![]() - частное решение уравнения
- частное решение уравнения ![]() .
.
Общая классификация дифференциальных уравнений