Для анализа переходных процессов при воздействии на цепь сигналов произвольной формы наряду с временным и операторным методом широко используется частотный метод анализа, базирующийся на спектральных представлениях сигнала.
Для непериодических сигналов используются спектральные представления, основанные на паре преобразований Фурье. Преобразование Фурье может быть получено предельным переходом от ряда Фурье (5.6). Для этого зададим непериодический сигнал f(t), удовлетворяющий условию абсолютной интегрируемости в бесконечных пределах (рис. 9.1):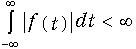 
. С физической точки зрения, это означает, что задается реализуемый сигнал с конечной энергией; при этом
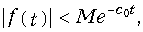
где М, с0 — положительные постоянные величины.
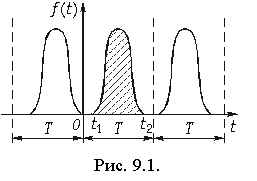
Условие (9.1) означает, что модуль |f(t)| имеет ограниченный показатель роста. Превратим мысленно этот сигнал в периодический повторением его через период Т (см. рис. 9.1). К полученному таким образом сигналу применимо разложение (5.6), которое после перехода к переменной t можно записать в виде
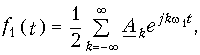
где
После подстановки Аk в уравнение (9.2) с учетом (9.3) получаем
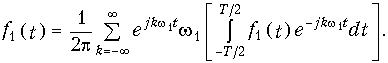
Переходя в уравнении (9.4) учитывая, что при этом w1 dw и kw1 w, а сумма вырождается в интеграл, получаем для исходного сигнала
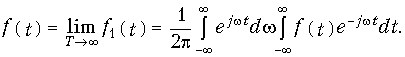
Внутренний интеграл в уравнении (9.5) носит название спектра сигнала F(jw):
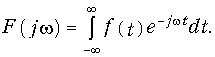
Тогда формула (9.5) принимает вид
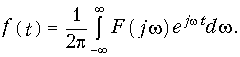
Уравнения (9.6) и (9.7) являются основными в теории спектрального анализа, причем (9.6) называется прямым, а (9.7) — обратным преобразованием Фурье. По аналогии с Аk спектр F(jw) является в общем случае комплексной функцией частоты и может быть записан в алгебраической форме
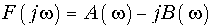
и показательной форме
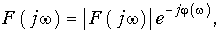
где
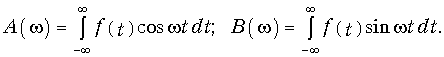
Модуль
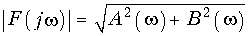
определяет амплитудный, а аргумент
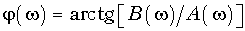
— фазовый спектр сигнала. Причем, как и для периодического сигнала, амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Физический смысл преобразования Фурье лучше всего проявляется при представлении обратного преобразования (9.7) в тригонометрической форме. Если подставить вместо F(jw) в (9.7) его значение из (9.9), то получим
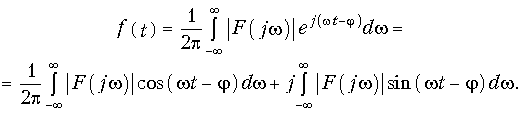
Учитывая, что |F(jw)| — четная, а синус — нечетная функция частоты интеграл от второго слагаемого равен нулю. Следовательно, принимая во внимание четность подынтегрального выражения в первом слагаемом, обратное преобразование Фурье имеет вид
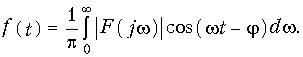
Из (9.13) следует важнейший вывод о том, что непериодический сигнал может быть представлен пределом суммы (интеграл) бесконечно большого числа бесконечно малых гармонических колебаний с амплитудами (1/p)|F(jw)| и начальными фазами j = j(w), причем, учитывая, что разность частот соседних гармоник бесконечно мала Dw = dw, то F(jw) в уравнении (9.13) представляет непрерывный сплошной спектр в отличии от спектра периодического сигнала, который является дискретным (линейчатым). Поэтому F(jw) называют комплексной спектральной плотностью, a |F(jw)| — спектральной плотностью амплитуд непериодического сигнала.
Смысл комплексного спектра F(jw) следует из связи между спектрами периодических и непериодических сигналов. Сравнение уравнений (9.3) с (9.6) позволяет установить эту связь между спектрами: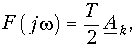 
и спектр комплексных амплитуд Ak обращается в комплексную спектральную плотность F(jw).
Из (9.14) следует и другой важный вывод: модуль спектральной плотности непериодического сигнала и огибающая линейчатого спектра периодического сигнала, полученного повторением с периодом Т непериодического сигнала, совпадают по форме и отличаются только масштабом. Это наглядно можно проиллюстрировать на примере периодической последовательности прямоугольных импульсов (см. рис. 5.3, а): с увеличением периода (скважности q) спектр становится гуще (см. рис. 5.4, б) и в пределе при T = ¥ периодический сигнал превращается в непериодический (рис. 9.2), а дискретный спектр обращается в сплошной (рис. 9.3). При этом огибающая как линейчатого, так и сплошного спектра описывается функцией отсчетов (5.29): sinx/x.
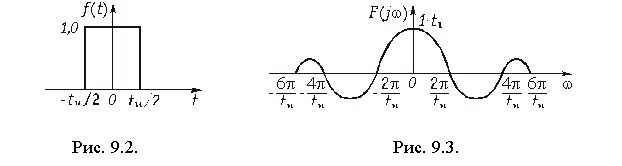
Рассмотрим некоторые основные свойства преобразования Фурье. Если сигнал f(t) является четной функцией времени, то, его спектр F(jw) — вещественный. Действительно, согласно (9.6) для F(jw) можно записать:
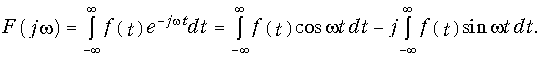
Второй интеграл равен нулю в силу нечетности подынтегральной функции, следовательно,
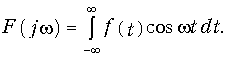
Аналогично при нечетности сигнала f(t) спектр F(jw) является чисто мнимым.
Важным свойством преобразования Фурье является взаимозаменяемость переменных t и w. Для четного сигнала f(t) и вещественного спектра F(jw) можем заменить в преобразовании (9.6) знаки перед jwt:
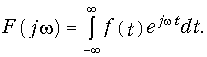
Тогда сравнивая (9.16) и (9.7) видим их подобие. Взаимозаменяемость переменных в преобразовании Фурье позволяет установить связь между частотными и временными характеристиками сигнала.
В соответствии с (9.8) и (9.9) сигнал может быть задан либо с помощью своего амплитудного |F(jw)| и фазового спектра j(w), либо с помощью вещественной A(w) и мнимой частей B(w) спектра сигнала. Причем, все они взаимосвязаны между собой согласно (9.11)—(9.12), т. е. нельзя задавать независимо амплитудный |F(jw)| и фазовый спектр j(w), или вещественную A(w) и мнимую часть спектра B(w).
Наиболее ясно эта связь проявляется для сигнала, заданного на положительной полуоси времени t:
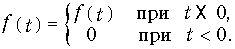
Перепишем (9.13) в форме
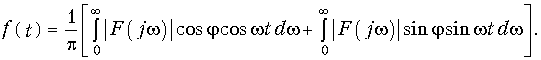
Или учитывая, что
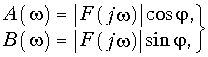
при t 
0 получим:
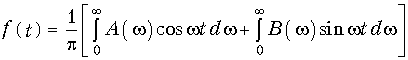
и при t < 0 с учетом (9.17)
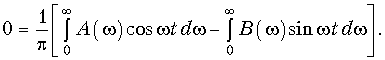
Суммируя и вычитая равенства (9.19) и (9.20), получаем:
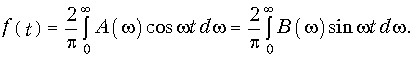
Отсюда следует связь между вещественной A(w) и мнимой B(w) частями спектра сигнала:
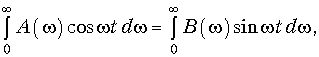
т. е. в данном случае сигнал f(t) полностью определяется только вещественной A(w) или мнимой B(w) частями комплексного спектра F(jw).
В заключение отметим, что при w = 0 спектр (9.6) принимает значение
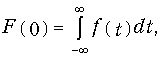
т. е. будет равен площади, ограниченной сигналом f(t). Формула (9.23) позволяет в ряде случаев оценить спектр сигнала по виду функции f(t).
Следует подчеркнуть, что временное и спектральное представление является просто двумя формами (моделями) представления реального физического процесса, и они лежат в основе временных и частотных методов анализа электрических цепей.
В заключение установим связь между преобразованием Фурье и преобразованием Лапласа. Если положить, что f(t) удовлетворяет условию (9.17), то прямое преобразование Фурье принимает вид
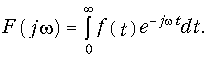
Соотношение (9.24) носит название одностороннего преобразования Фурье, так как оно определяется на положительной полуоси t. Если принять в качестве частного случая в формуле (7.1) a = 0, то р = jw, и прямое преобразование Лапласа (7.2)
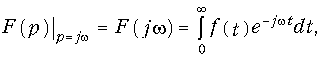
т. е. полностью совпадает с односторонним преобразованием Фурье (9.24).
Аналогично получим для обратного преобразования Лапласа (7.4) с учетом того, что dp = jdw:
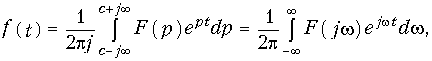
что полностью совпадает с (9.7).
Таким образом, преобразование Фурье есть частный случай преобразования Лапласа при a = 0. Следует подчеркнуть, что преобразование Фурье имеет более узкую область применения, чем преобразование Лапласа, так как условие (9.1), которым должны удовлетворять функции, преобразуемые по Фурье более жесткое, чем условие (7.3). Всякая функция, для которой применимо преобразование Фурье (9.6) всегда может быть преобразована по Лапласу, но не наоборот. В этой связи изображение F(p) можно трактовать как своего рода обобщенный спектр сигнала f(t).