3.1. Классификация широкополосных сигналов

3.2. Квазиортогональные двоичные последовательности

3.3. М-последовательности и их свойства

3.4. Предпочтительные пары М-последовательностей

3.5. Максимальные связные множества М-последовательностей

3.6. Составные последовательности на основе двух и более М-последовательностей

3.7. Примеры применения псевдослучайных последовательностей

3.8. Основная информация

3.1. Классификация широкополосных сигналов

При выборе ансамбля сигналов для ААСС обычно принимают во внимание следующие свойства широкополосных сигналов:

• объем ансамбля и база сигналов,
• корреляционные и взаимные корреляционные свойства сигналов,
• правило формирования сигналов ансамбля,
• техническая реализация генераторов ШПС и устройств их обработки.

В ААСС объем ансамбля сигналов определяется прежде всего числом абонентов в системе. Как указывалось в предыдущих главах, объем ансамбля сигналов должен быть равен числу абонентов или превышать его в 2 раза. При необходимости обеспечения «многоадресности» абонентов (см. §1.1) объем ансамбля должен быть увеличен на порядок и более.

База сигнала, в ААСС обычно значительно превосходящая 1, определяется допустимым уровнем внутрисистемных помех. Как было показано в §2.1, с увеличением базы уровень внутрисистемных помех уменьшается. Кроме того, при большой базе можно обеспечить режим скрытой связи, когда сигнал находится «под шумом». Величина базы определяет также объем ансамбля.

Корреляционные и взаимные корреляционные свойства сигналов - одни из основных характеристик, которые определяют возможность использования того или иного ансамбля сигналов. Взаимные корреляционные функции должны иметь «малые» значения максимальных и боковых выбросов, в некоторых случаях достаточно нормализации распределения значений ВКФ с малой дисперсией. Корреляционные и взаимные корреляционные функции – это временные характеристики сигналов, определяющие степень зависимости сигналов при различных временных сдвигах. Сигналы еще характеризуются частотной корреляционной функцией /2, 16/, определяющей степень связанности сигналов при частотном сдвиге. В пространстве над плоскостью (время-частота) временная и частотная корреляционные функции образуют поверхность, которая называется поверхностью (функцией) неопределенности /16, 18/. Частотные корреляционные функции приобретают очень важное значение при связи с объектами, движущимися с большой скоростью, например, в спутниковых системах связи.

Для обеспечения простоты технической реализации генератора ШПС следует использовать регулярные методы формирования сигналов, т.е. в соответствии с каким-то правилом. Для ААСС важна не только простота технической реализации самого генератора, но и простота и оперативность смены сигнала, перехода на другой адрес.

По характеру изменения сигнала во времени можно разделить ШПС на сигналы с аналоговой и дискретной модуляцией (амплитудной, фазовой, частотной). Среди сигналов с аналоговой модуляцией широко известны сигналы ЛЧМ - с линейной частотной модуляцией, у которых несущая частота в течение длительности Т меняется по линейному закону (рис.3.1). Эти сигналы несложно генерировать, но они имеют малый объем ансамбля: сигналы могут различаться только девиацией частоты. В силу этого ЛЧМ - сигналы в ААСС находят очень ограниченное применение и далее рассматриваться на будут.

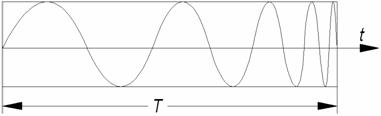
Рис. 3.1. ЛЧМ - сигнал

В ААСС широко используются сигналы с дискретной модуляцией - манипулированные по фазе, амплитуде и частоте.

Фазо- и амплитудно – манипулированные сложные сигналы часто формируются с использованием двоичных псевдослучайных последовательностей (ПСП), которые манипулируют по фазе или амплитуде несущую (поднесущую) частоту. На рис. 3.2 представлены примеры АМ и ФМ сложных сигналов. База сигнала B=FT определяется длиной последовательности N. Действительно, спектр сигнала определяется длительностью элемента последовательности F=1/τ_Э. В течении длительности сигнала Т укладывается N элементов, т.е. τ_Э=T/N и F=N/T, а В=N. На рис. 3.2 в ПСП используется 7 элементов, и база АМ и ФМ сложных сигналов В=7.

В передатчике AM и ФМ сложные сигналы получить довольно просто (рис.3.3.). На один вход перемножителя подается двоичная последовательность с генератора ПСП, а на другой – поднесущая частота. При AM двоичная последовательность представляется в виде последовательности 1 и 0, а при ФМ - двоичная последовательность должна быть преобразована в последовательность символов +1 и -1. Для этих видов сигналов техническая реализация генератора ШПС будет определяться в основном технической реализацией генератора псевдослучайной последовательности.

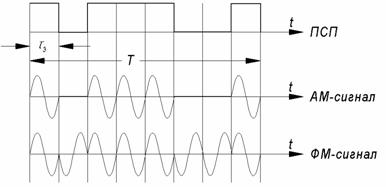
Рис.3.2. АМ- и ФМ – сложные сигналы

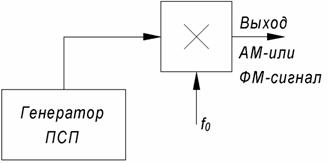
Рис.3.3. Формирователь сложного АМ- или ФМ - сигнала

Корреляционные функции AM и ФМ сложных сигналов определяются корреляционными функциями манипулирующих последовательностей. На рис.3.4 представлен процесс вычисления корреляционной функции AМ и ФМ сложных сигналов, манипулированных двоичной последовательностью 1110010 и сдвинутой на три элемента 0010111 последовательности.

Значения корреляционной функции получаем на выходе интегратора в момент t=T. Как видно из рис.3.4, на выходе перемножителя будут аналогичные сигналы и для манипулированных сигналов, и для ПСП. Отличие будет в абсолютном уровне сигналов. Оно будет проявляться на выходе интегратора в незначительном уменьшении напряжения в момент отсчета t=T для манипулированных сигналов (примерно 20 %). Относительные же соотношения между значениями КФ сохраняются.

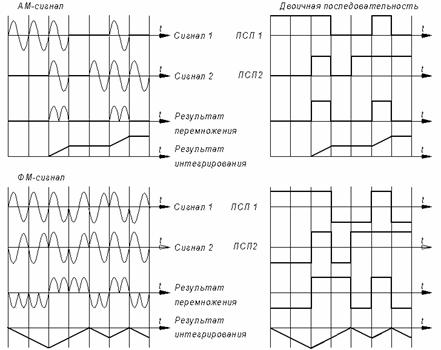
Рис.3.4. Процесс вычисления корреляционных функций сложных сигналов.

Поэтому, рассматривая КФ сложных AM или ФМ сигналов, достаточно анализировать корреляционные функции манипулирующих последовательностей.

Следует также отметить, что для подобных сигналов достаточно вычислить КФ в дискретных точках iτ_Э. В остальных точках значения получаются путем соединения вычисленных значений в дискретных точках прямыми линиями.

Фазоманипулированные сложные сигналы находят более широкое применение чем АМ – сигналы в силу более эффективного использования пиковой мощности передатчика и более высокой помехоустойчивости. Поэтому в дальнейшем при рассмотрении ПСП и их свойств ограничимся двоичными последовательностями, состоящими из элементов +1 и -1.

Сигналы с дискретной частотной модуляцией, называемые также дискретно-частотными сигналами (ДЧ – сигналы), получаются в результате скачкообразного изменения частоты несущей по какому-то закону в заданном диапазоне частот. Закон, или программа перестройки частоты, известен на передающей и приемной сторонах. На рис.3.5 представлен один из вариантов ДЧ - сигнала.

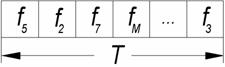
Рис.3.5. Дискретно-частотный сигнал

Сигнал длительностью Т состоит из М элементов, каждый из которых передается на своей частоте. Обычно используются М частот и М временных позиций, элементов сигнала. Основным преимуществом ДЧ - сигнала является получение большой базы при относительно небольшом числе элементов.

В интервале времени Т укладывается М временных элементов; каждый элемент длительности Т/М передается на своей частоте, ширина спектра при этом равна F₁=1/τ_Э=М/Т.

Весь сигнал имеет спектр в М раз шире, так как используется М различных частот: F=M·F₁. База ДЧ - сигнала

. (3.1)

При числе элементов М=10 база сигнала будет равна В=100, а для получения базы В=10³ следует использовать сигнал, состоящий примерно из 30 элементов.

Одна из возможных схем формирования ДЧ - сигнала представлена на рис.3.6 /16/ .

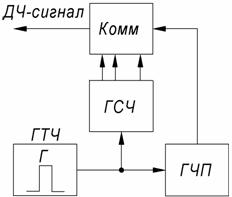
Рис.3.6. Формирователь ДЧ – сигнала

Генератор тактовой частоты (ГТЧ) синхронизирует работу генератора сетки частот (ГСЧ) и генератора числовой последовательности (ГЧП). Генератор числовой последовательности выдает случайную последовательность чисел от 0 до M-1, которые подаются на управляющий вход цифрового коммутатора (Комм); цифровой коммутатор ставит в соответствие каждому числу заранее определенный сигнал сетки частот. Синхронизация генератора сетки частот и генератора числовой последовательности позволяет получить сигнал на выходе цифрового коммутатора без скачков фазы. Сравнение рис. 3.6 и 3.3 показывает, что для формирования ДЧ - сигнала используется более сложное устройство. ДЧ - сигналы изучены недостаточно полно. Для оценки корреляционных свойств ДЧ - сигналов можно привести следующие данные, полученные в /23/. При ограничении выбросов ВКФ и боковых выбросов КФ значением 1/M объем ансамбля сигналов будет небольшим - порядка М. Увеличение объема ансамбля приведет к увеличению боковых выбросов КФ. Однако благодаря положительному свойству обеспечивать большую базу при относительно небольшом числе элементов ДЧ - сигналы привлекают внимание специалистов. Основной проблемой, которая требует своего разрешения является получение большого ансамбля сигналов с «хорошими» корреляционными свойствами.

Для увеличения объема ансамбля с сохранением корреляционных свойств используются комбинированные методы модуляции, например, частотная и фазовая, частотная и амплитудная и т.д. Для получения ДЧ-ФМ сложного сигнала каждый элемент ДЧ - сигнала манипулируется по фазе ПСП длиной N. База сигнала будет B=M²·N, при этом следует ожидать значительного уменьшения значений боковых выбросов.

Итак, в AAСC наибольшее применение находят ФМ сложные сигналы. Поэтому дальнейшее изложение будет касаться двоичных последовательностей, состоящих из элементов +1 и -1. Будут рассмотрены последовательности, которые при относительной простоте генерации позволяют обеспечить большие базы и большие ансамбли с «хорошими» корреляционными свойствами.

3.2. Квазиортогональные двоичные последовательности

Для формирования сложных сигналов используются ортогональные и квазиортогональные двоичные последовательности.

Ортогональные последовательности (Уолша, Хаара, Радемахера и др.) имеют небольшой ансамбль, равный или меньший их длине, и ортогональность только в точке, т.е. при нулевом сдвиге. Их взаимные корреляционные функции имеют большие боковые выбросы. В связи с этим ортогональные последовательности для систем со свободным доступом при разделении по форме находят очень ограниченное применение: их использование возможно только в синхронных адресных системах, а также при комбинационном объединении.

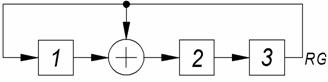
Для систем со свободным доступом целесообразно использовать такие двоичные сигналы, которые имеют минимальные боковые выбросы (см. §2.2, а также /2/). Такие последовательности называются квазиортогональными. Среди квазиортогональных сигналов наибольшее применение нашли так называемые М-последовательности. Свойства этих последовательностей составленных из двоичных элементов, будут подробнее изложены в последующих разделах. Здесь же укажем только на их отличительные особенности. М-последовательности формируются с помощью регистра сдвига с m разрядами, охваченного обратными связями через сумматор по модулю 2 (линейная обратная связь). Обратные связи устанавливаются в соответствии с проверочным полиномом. Проверочные полиномы найдены до степени . Длина последовательности , т.е. при небольшом числе разрядов регистра можно получить довольно длинные последовательности. Так, например, при получаем последовательность длиной 1023. Это определяет простоту технической реализации генератора М-последовательности. Кроме того, М-последовательности имеют хорошие периодические корреляционные функции: боковые выбросы ПКФ принимают одно значение, равное -1. Все это обусловило широкое применение М-последовательностей и глубокое изучение их свойств.

При установлении нелинейной обратной связи в регистре сдвига с m разрядами получаем нелинейную рекуррентную последовательность длиной . Эти последовательности позволяют получить очень большие объемы ансамблей: . При , можно получить 13 последовательностей, а при , более последовательностей. Это их положительное свойство. Однако это сопряжено пока с некоторыми трудностями, связанными с определением вида нелинейной обратной связи. Кроме того, нелинейный характер обратной связи приводит к значительным трудностям при их исследовании. Только этим можно объяснить очень скудные сведения об этих последовательностях.

Большим классом являются составные двоичные последовательности, которые образуются из двух и более исходных последовательностей. Составные последовательности формируются для увеличения объема ансамбля сигналов, для получения большой длины последовательности, в том числе и при ограничении быстродействия используемых микросхем.

Составные последовательности могут быть образованы из исходных М-последовательностей одинаковой длины для увеличения объема ансамбля. К этим последовательностям можно отнести последовательности Гоулда, сформированные путем поразрядного сложения по модулю 2 М-последовательностей, а также последовательности, сформированые на основе более двух последовательностей (некоторые из них будут рассмотрены ниже). Одна из исходных М-последовательностей может быть меньшей длины (например, при получении последовательностей Касами, которые также подробнее будут рассмотрены).

На рис. 3.7 представлена структурная схема генератора последовательностей Гоулда.

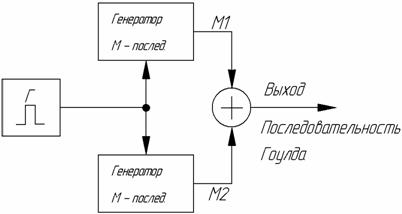
Рис.3.7. Схема формирования последовательностей Гоулда на основе двух М-последовательностей

Все исходные последовательности могут иметь различную длину. Этот метод получения составных сигналов используется для формирования очень длинных последовательностей. Например, последовательность длиной можно составить из 5 последовательностей с относительно простыми периодами: 25, 27, 29, 31 и 32 /14/. Исходные последовательности могут объединяться с помощью мажоритарного правила (при нечетном числе исходных последовательностей) или поэлементного суммирования по модулю 2. Составные последовательности, образованные по такому принципу, обеспечивают малое время поиска, быстрое вхождение в синхронизм. Но они имеют большие боковые выбросы на периодах исходных последовательностей. Для передачи информации в системах с разделением по форме сигналов эти последовательности могут найти ограниченное применение.

Для увеличения длины последовательности при ограниченном быстродействии микросхем можно использовать сложение исходных М-последовательностей со сдвинутыми тактовыми интервалами /4/.

На рис.З.8а представлена схема формирования таких последовательностей на основе двух М-последовательностей, а на рис.3.86 - последовательность, полученная путем сложения двух М-последовательностей одинаковой длины . Длина вновь образованной последовательности будет в два раза больше .

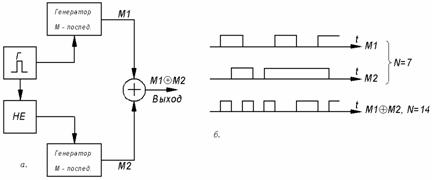
Рис.3.8. Принцип формирования длинных последовательностей при ограниченном быстродействии микросхем

Особое положение занимают последовательности Баркера, которые имеют хорошие апериодические КФ: уровень боковых выбросов при любой длине не превышает 1. Однако эти последовательности имеют небольшую длину (известны последовательности Баркера длиной 3,4,5,7,9,11,13). Для каждой длины существует одна последовательность. С учетом циклических сдвигов объем ансамбля равен длине последовательности. И длина, и объем ансамбля явно недостаточны для использования этих последовательностей в РТС со свободным доступом и РКФ.

3.3. М-последовательности и их свойства

М-последовательности находят широкое применение для формирования широкополосного сигнала. Они используются сами непосредственно для модуляции несущей или на их основе формируются двоичные последовательности, называемые составными /2/. Это обусловлено прежде всего тем, что М-последовательности имеют очень хорошие ПКФ и генерируются с помощью простой схемы: m - разрядного регистра, охваченного обратной связью через сумматор по модулю 2. Причем длина последовательности, определяемая как , практически не ограничена: известны М-последовательности длиной до . Из всех двоичных последовательностей М-последовательности наиболее полно изучены. Рассмотрим подробнее их свойства и характеристики.

М-последовательности называют также последовательностями максимальной длины, последовательностями сдвигового регистра, линейными рекуррентными последовательностями. Длина последовательности . Это максимальная длина, которую можно получить с помощью регистра сдвига с m разрядами с линейной обратной связью.

Каждая М-последовательность характеризуется проверочным полиномом

,

который определяет проверочное уравнение

, (3.2)

или

. (3.3)

В выражениях (3.2) и (3.3) суммирование проводится по модулю 2, коэффициенты могут принимать значения 0 или 1. Выражение (3.3) есть рекуррентное правило определения любого символа М-последовательности по предыдущим m символам.

Последовательность коэффициентов представляет собой так называемое характеристическое уравнение /18/, которое определяет обратные связи в генераторе М-последовательности: j-й разряд регистра сдвига подключен к обратной связи (ко входу сумматора по модулю 2), если , выход j-го разряда не связан с сумматором по модулю 2, если .

На рис.3.9 представлен генератор М-последовательности, построенный в соответствии с проверочным полиномом . Характеристическое уравнение 100101. Этот полином имеет степень и дает М-последовательность длиной . В схеме генератора выходы третьего и пятого разрядов регистра сдвига подключаются к обратной связи, так как , а означает, что выход сумматора по модулю 2 связан со входом регистра сдвига.

67

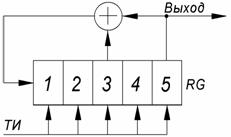
Рис.3.9. Генератор М-последовательности длиной , проверочный полином , характеристическое уравнение I00I0I

Полиномы для сокращения записи обозначают в восьмеричном представлении /10/: характеристическое уравнение справа разбивается на группы по три двоичных символа, если в последней группе число символов окажется меньше трех, то слева дописывается соответствующее число нулей, каждая группа прочитывается как двоичное число. Например, используемый выше полином , имеющий характеристическое уравнение 100101, можно записать в восьмеричном коде как 45, а характеристическое уравнение для 10000001001 (проверочный полином ) запишется как 2011. Все проверочные полиномы заданной степени пронумерованы. Условно выбирается полином 1 - это полином с минимальным числом ненулевых коэффициентов. Для этого полинома можно определить α, которое является корнем уравнения , α называется примитивным элементом. Полином за номером 3 имеет корень уравнения , - третью степень примитивного элемента и т.д. Таким образом, номер полинома совпадает со степенью примитивного элемента , которая обращает в нуль рассматриваемый проверочный полином. Номера полиномов и их восьмеричное представление приведены в /10/ для и в приложении /1/ для .

Пример. Полином 45 для приводится в приложении 1 под номером 1, полином под номером 3 записывается как . Покажем, что если α – корень уравнения , т.е. , то является корнем уравнения

, т.е. . Подставляем в , получим

.

Но и .

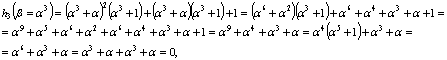т.е. показано, что является корнем уравнения .

Именно номера полиномов будут использоваться при рассмотрении составных последовательностей с хорошими корреляционными свойствами.

Остановимся подробнее на свойствах М-последовательностей /1, 4,12,18/. Схема генератора М-последовательности, аналогичная представленной на рис.3.9, может давать N различных последовательностей в зависимости от начального состояния регистра сдвига. Все эти последовательности будут циклическими сдвигами одной последовательности.

М-последовательность содержит «единиц» и «нулей». Вес последовательности (число «единиц») . В последовательности содержатся все возможные комбинации из m двоичных символов, кроме комбинации, состоящей из одних нулей. Это свойство обусловило название М-последовательностей как последовательностей максимальной длины.

Например, М-последовательность 0010111 содержит 4 «единицы» 3 «нуля». Вес последовательности равен 4. Количество «единиц» и «нулей" не будет меняться при циклических сдвигах последовательности: по 4 «единицы» и 3 «нуля» будет содержаться и в последовательности 1110010, и в других циклических сдвигах. Рассмотренные последовательности будут содержать все возможные комбинации по 3 символа: последовательность 0010111.001… можно представить последовательностью комбинаций 001, 010, 101, 011, 111, 110, 100. Порядок следования комбинаций будет различным для различных последовательностей. Это как раз определяет случайный характер М-последовательностей, поэтому они относятся к классу псевдослучайных последовательностей (ПСП).

В М-последовательности содержится блоков, т.е. последовательностей одинаковых элементов. Например, в последовательности 0010111 содержится 4 блока: 00, 1, 00, 111. Такое число блоков приближает М-последовательность к оптимальным последовательностям, которые имеют малые значения максимальных боковых выбросов КФ. Для оптимальной системы число блоков должно быть равным /2/.

М-последовательность имеет двухуровневую ПКФ: , , независимо от длины . Значение является минимальным для длины при любом m, что и определяет оптимальность М-последовательности. Разница между главным выбросом ПКФ и ее боковыми выбросами при увеличении возрастает, и при ПКФ М-последовательности приближается к КФ гауссовского белого шума, которая представляется в виде дельта-функции , - спектральная плотность шума.

На рис.3.10 представлена ПКФ М-последовательности.

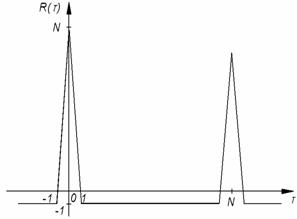
Рис.3.10. Периодическая корреляционная функция М-последовательности

Одно из важнейших свойств М-последовательностей - свойство сдвига и сложения, которое заключается в том, что поэлементная сумма по модулю 2 двух циклических сдвигов даст ту же М-последовательность со сдвигом, отличным от двух исходных. Если обозначить через - к-ый сдвиг, то свойство сдвига и сложения можно записать в виде:

. (3.4)

В /1/ дана методика определения номера сдвига i, который получается при сложении k – го и j – го циклических сдвигов одной последовательности с проверочным полиномом . В этой работе введено начало отсчета, т.е. нулевой циклический сдвиг – это М-последовательность с начальным блоком, состоящим из первых «нулей» и одной «1» (на последнем месте).

Таким, образом, 00...01 - начальный блок нулевого циклического сдвига М-последовательности. Фактически - это начальные состояния разрядов регистра сдвига генератора М-последовательности с вынесенными сумматорами (рис.3.9), при этом «1» записывается в первый разряд, а в остальные – «0». При таком определении нулевого циклического сдвига свойство сдвига и сложения (3.4) можно записать в виде:

. (3.5)

Это уравнение - сравнение по модулю означает, что двучлен является остатком от деления на , при этом следует иметь в виду, что все операции (сложение, умножение, деление) проводятся по модулю 2.

Каждый циклический сдвиг можно записать вариантами сумм из двух других циклических сдвигов и единственным образом в виде суммы из n циклических сдвигов, номера которых меньше m , при этом n может принимать значения от 1 до m:

, (3.6)

коэффициенты принимают два значения 0 или 1; при этом среди всех m значений этих коэффициентов только n равны 1, а остальные - 0, .

Пример. Определим, в виде каких сумм циклических сдвигов можно представить и при . Для этого проводим деление и на .

	- 1-й остаток
	- 2-й остаток
	- 3-й остаток .

В результате деления получили 3 вида остатков, которые дают представление шестого циклического сдвига в виде соответствующих сумм .

Пятый циклический сдвиг можно представить суммой уже из 3 циклических сдвигов, номера которых меньше .

Состав суммы (3.6), т.е. значения коэффициентов , можно определить, используя генератор М-последовательности со встроенными сумматорами. На рис. 3.11 представлена такая схема для , . Под соответствующими разрядами RG представлены их состояния в последующих тактах (слева записаны номера тактов). Состояние i -го разряда дает значение коэффициента , а номер такта совпадает с номером циклического сдвига. Справа записаны суммы вида (3.6) для различных циклических сдвигов.

Разберем еще одно свойство М-последовательностей, которое редко приводится в литературе. Это свойство определяет связи между последовательностями, их проверочными полиномами.

Оказывается, если - М-последовательность с номером , а - любое число, , то последовательность , полученная выбором элементов -й последовательности , также является М-последовательностью. При этом, при , получается та же -я последовательность, только другой ее циклический сдвиг. Если и наибольший общий делитель , то полученная последовательность имеет ту же длину , и ее номер определяется из соотношения

. (3.7)

Номер такта	Состояние RG
	а0	а1	а2
0	1	0	0
1	0	1	0
2	0	0	1
3	1	1	0
4	0	1	1
5	1	1	1
6	1	0	1
7	1	0	0

Рис.3.11

Если , получим М-последовательность меньшей длины . Операция преобразования одной последовательности в другую (или в другой циклический сдвиг) называется децимацией по индексу /12/. Рассмотрим связи между последовательностями и полиномами на примере.

Пример. Последовательность длиной , , находящаяся в приложении 1 под номером 1, характеризуется проверочным полиномом и имеет вид: 0000100101100111110001101110101. Составим последовательность из ее элементов: 0010010110011111000110111010100. Сопоставление полученной последовательности с исходной позволяет сделать вывод, что получена та же последовательность, но другой циклический сдвиг.

Составим последовательность из 3к-х элементов последовательности 1. Получим последовательность: 0001010110100001100100111110111, которая является 20-м циклическим сдвигом последовательности 3, характеризующейся проверочным полиномом .

Рассмотрим другие индексы децимации .

приводят к последовательности 1. приводит к последовательности 5 с проверочным полиномом . К этому же полиному приводят децимации по . Покажем это для . Полинома с номером 9 в таблице нет. Используем свойство, что умножение номера полинома на - приводит к той же последовательности. Проводим умножение 9 на 2 последовательно 5 раз (можно делить на 2), результата представляем по модулю 31. Получим: 9, 18, 36 = 5, 10, 20, 40 = 9. Из полученных значений выбираем минимальное, которое и определяет номер полученного полинома.

К полиному 3 приводят, кроме , еще децимации по индексам: . Децимации по индексу приводят к полиному 7 (а также ). Децимация даст последовательность 11 с проверочным полиномом (а также ). Децимация с приводит к последовательности 15 с проверочным , а также .

Из рассмотренного примера можно сделать вывод, что все М-последовательности длиной 31 связаны между собой с индексами децимации

. Все рассмотренные связи можно привести в виде диаграммы (рис.3.12).

Выше определены связи одного полинома с другими. Теперь нетрудно установить связи всех полиномов между собой. Для этого просмотреть цепи переходов полиномов при различных .

Пусть . Переход полинома 1 в полином 3 условно обозначим . Полином 3 при переходит в полином 5: . Цепь продолжается: . Дальнейшие вычисления дают, что . Таким образом, имеем замкнутую цепь, в которой участвуют все полиномы:

.

Эта цепь на рис.3.12 представлена в виде шестиугольника.

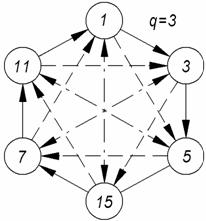
Рис.3.12. Диаграмма децимаций М-последовательности длиной - при обходе по часовой стрелке и - при обходе против часовой стрелки, и соответственно,

Следует отметить, что при обходе цепи в одном направлении имеем децимации с , а при обходе в другом направлении получаем децимации с (переход указывает на значение индекса децимации так же, как переход ).

Пусть теперь . С этим индексом децимации имеем цепь , в которой участвует только половина полиномов. При обходе в обратном направлении имеем . Вторая цепь объединяет другие полиномы: , Эти цепи представлены на рис.3.12 в виде треугольников.

Наконец, пусть . Это дает попарную связь полиномов: - полином 1 переходит в полином 15 с , и полином 15 переходит в полином l с таким же индексом децимации. Следует отметить, что . определяет связь обратных полиномов: полином 15 является обратном первому. Другие пары обратных полиномов: и .

Таким образом, все полиномы образуют объединенную систему, что хорошо видно на рис.3.12.

3.4. Предпочтительные пары М-последовательностей

М-последовательности находят широкое применение благодаря относительной просторе их генерации, а также «хорошей» периодической функции корреляции. Однако в ряде применений, в частности в многоканальных системах со свободным доступом, основной характеристикой сигналов является их функция взаимной корреляции. Для этой функции М-последовательности в общем случае дают большие выбросы. Как указано в /12/, максимальный выброс периодической функции взаимной корреляции достигает величины , где - длина последовательности.

Однако среди М-последовательностей заданной длины можно выбрать такие пары последовательностей, для которых взаимные периодические корреляционные функции имеют три уровня:

. (3.8)

где - целая часть числа .

Эти пары М-последовательностей называют предпочтительными парами /12/.

В ряде работ /12,18/ показано, что номера и предпочтительных пар полиномов должны быть связаны между собой соотношением

, (3.9)

где - определяющий номер, принадлежит полной группе номеров полиномов заданной степени. В указанных выше и других работах определены значения , дающие предпочтительные пары, для . Для некоторых значения приведены в табл.3.1.

Таблица 3.1

Чтобы выбрать полином, составляющий с заданным полиномом предпочтительную пару, надо провести умножение на одно из значений , приведенных в табл.3.1. Если результат не принадлежит полной группе полиномов заданной степени, то значение следует уточнить. Для этого полученное значение надо раз умножить или разделить на 2 по модулю . Минимальное значение из всех полученных результатов и будет уточненным номером парного полинома.

Для определения предпочтительных пар удобно пользоваться диаграммой децимаций. Воспользуемся рис. 3.12 для определения предпочтительных пар для . Для этой длинны предпочтительные пары образуются при (табл.3.1).

Поэтому полином 1 составляет предпочтительную паpу с полиномами 3 и 5, а также с полиномами 11 (переход от полинома 11 к полиному 1 при ) и с полиномом 7 (переход от полинома 7 к полиному I при ). Аналогично можно найти предпочтительные пары для любого полинома. Например, полином 3 образует предпочтительные пары с полиномами 5 и 15, а также с полиномами 1 и 11. Для только связь с не дает предпочтительной пары.

Определим предпочтительные пары для , .

Найдем для полинома 7 предпочтительные пары:

,

, .

Следовательно, получены следующие предпочтительные пары, содержащие полином 7:

7-35, 7-91, 7-119, 7-343, 7-127.

На рис.3.13 приведена диаграмма предпочтительных связей полиномов для . Все 60 полиномов разбиваются на две группы, в каждой группе полиномы располагаются по окружности. При обходе окружности по часовой стрелке номер последующего полинома определяется по формуле (3.9) при . Связи, соответствующие , показаны между всеми полиномами. Остальные предпочтительные связи при показаны только для полинома 1, чтобы не загромождать рисунок. Такие же связи существуют для каждого полинома. Для определения связей полиномов из внутренней группы следует поменять местами внутреннюю и внешнюю окружности.

Часто представляет интерес не только значение корреляционной, функции, но и вес каждой из них. В этом случае говорят о взаимно, корреляционном спектре. Предпочтительные пары имеют трехуровневый спектр:

77

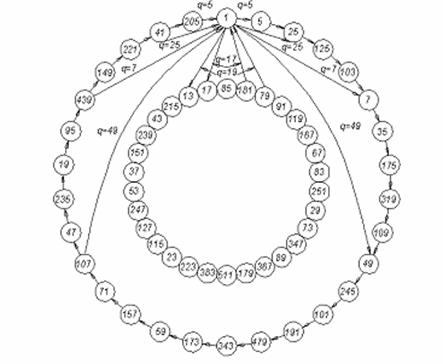
Рис.3.13. Предпочтительные пары для полинома 1,

уровень встречается раз,

уровень -1 встречается раз,

уровень встречается: раз,

где .

Пример. Найти взаимный корреляционный спектр для , , .

Уровень -65 встречается 120 раз,

уровень -1 встречается 767 раз,

уровень +63 встречается 136 раз.

3.5. Максимальные связные множества М-последовательностей

Предпочтительные пары М-последовательностей могут объединяться в множества, которые называются связными. В таком множестве любая пара является предпочтительной. Мощность таких множеств, т.е. число полиномов, входящих в одно множество, различно - от 0 до максимального значения . Связное множество максимальной мощности называется максимальным связным множеством. В табл.3.2, взятой из /12/ , приводятся мощности множества всех М-последовательностей и максимальных связных множеств, а также максимальные значения взаимной корреляционной функции для всех М-последовательностей и для предпочтительных паp .

Таблица 3.2

Мощности множеств М-последовательностей и максимальных связных множеств и максимальные значения их корреляционных функций

Анализ табл.3.2 позволяет сделать следующие выводы:

ансамбль М-последовательностей небольшой. Например, для имеется только 60 М-последовательностей;

предпочтительные пары при имеют меньшие значения боковых выбросов корреляционной функции, чем все множество М-последовательностей, и с ростом эта разница увеличивается. Иными словами, предпочтительные пары целесообразно использовать при большой длине последовательностей ;

число М-последовательностей, составляющих максимальное связное множество, является небольшим, . При предпочтительные пары отсутствуют, и для . Максимальное значение принимает для небольшой длины последовательности . Это значит, что можно определить такие шесть М-последовательностей, которые дадут трехуровневый взаимно-корреляционный спектр. На рис.3.14 представлена диаграмма предпочтительных связей для . На диаграмме стрелки указывают направление определения номера полинома при заданном .

Чтобы не загромождать рисунок, предпочтительные связи с показаны только для полинома 1. Аналогичные связи существуют для каждого полинома.

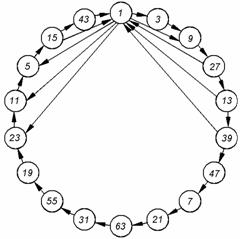
Рис.3.14. Диаграмма предпочтительных связей для (каждые 6 последовательных полиномов образуют максимальную связную систему)

Для длины . На рис.3.15 представлена диаграмма максимальных связных множеств для . Для связи не приведены, чтобы не загромождать чертеж, хотя эти связи также образуют максимальную связную систему мощностью . Значение дает только одну предпочтительную пару - мощность связного множества равна 2.

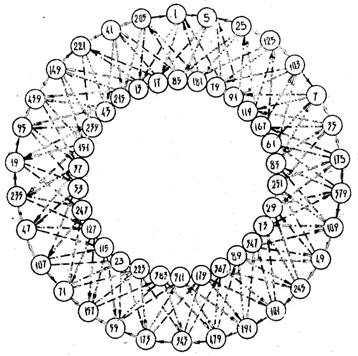
Рис.З.15. Максимальные связные множества для

В соответствии с рис.3.15 можно привести следующие примеры максимальных связных множеств, содержащих полином 1:

1-5-17, 1-13-17, 1-13-205, 1-205-181, 1-79-181, 1-5-79, а также 1-25-181, 1-41-17, (), 1- 49-107 (),

Аналогично можно составить максимальные связные множества для любого полинома.

3.6. Составные последовательности на основе двух и более М-последовательностей

Как показано в §3.1, на основе М-последовательностей можно построить ансамбль квазиортогональных двоичных последовательностей, объем которого во много раз превосходит число М-последовательностей.

Эти составные последовательности образуют последовательности немаксимальнои длины, проверочные полиномы которых могут быть представлены произведением проверочных полиномов исходных М-последовательностей . Для их формирования можно использовать регистр сдвига, охваченный обратными связями в соответствии с полиномом , число разрядов регистра определяется его степенью. Эти последовательности можно также формировать с использованием регистров сдвига, охваченных обратными связями в соответствии с полиномами . Выходы регистров сдвига суммируются по модулю 2. Длина последовательности равна - наименьшему общему кратному длин исходных последовательностей.

Среди таких последовательностей широко известны последовательности Гоулда, которые формируются на основе двух М-последовательностей одинаковой длины . Структурные схемы генератора последовательностей Гоулда для представлены на рис.З.16 (а - при использовании 10-разрядного регистра сдвига, б - при использовании двух 5-разрядных регистров).

Любое относительное изменение сдвигов исходных М-последовательностей приводит к формированию, новой последовательности. Поэтому ансамбль последовательностей Гоулда равен : он состоит из различных последовательностей, формируемых при различных сдвигах, и двух исходных М-последовательностей.

Самым интересным в этом методе формирования большого ансамбля сигналов является то, что при выборе предпочтительных пар исходных последовательностей корреляционная функция вновь образованной последовательности принимает такие же три значения , как и корреляционная функция исходных предпочтительных пар. В отличии от М-последовательностей для последовательности Гоулда трехуровневыми будут периодические и авто- и взаимно корреляционные функции.

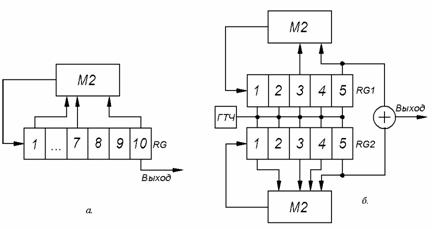
Рис.3.16. Формирование последовательностей Гоулда,

Для увеличения ансамбля сигналов можно использовать сложение по модулю 2 трех М-последовательностей одинаковой длины. Ансамбль сигналов при этом будет равен : слагаемое обусловлено различными сдвигами двух исходных последовательностей относительно третьей, a - это число последовательностей при сложении двух М-последовательностей из трех. Например: для ансамбль последовательностей Гоулда будет содержать более сигналов длиной .

Такая простая возможность получения большого ансамбля сигналов очень заманчива. В некоторых работах, например в /4/, указано на такую возможность. Однако сведения о корреляционной функции отсутствуют.

Исследования для , показали, что некоторые максимальные связные множества могут дать трехуровневые корреляционные функции. Назовем эти множества предпочтительными тройками. В этих тройках связи между исходными полиномами определяются соотношением

, (3.10)

где и связаны подобным соотношением

, (3.11)

причем , и принадлежат группе номеров , определяющих предпочтительные пары (см. табл.3.1).

Для определены номера , ,.

На рис.3.17 представлены предпочтительные тройки для . На этом рисунке для наглядности номера полиномов расставлены в две линии (а не 2 окружности, как на рис.3.13 и 3.15). Предпочтительные тройки образуются вершинами заштрихованных треугольников. Например, предпочтительными тройками, содержащими полином 1, будут: 1-181-79, 1-5-I7, 1-205-13. Для имеется всего 60 предпочтительных троек, и каждая тройка дает ансамбль объемом более последовательностей.

Исследование периодических корреляционных функций последовательностей Гоулда, сформированных на основе трех М-последовательностей, было проведено на ЭВМ для . Были проверены различные максимальные связные множества, в том числе предпочтительные тройки. Только предпочтительные тройки давали трехуровневые корреляционные функции. Однако при некоторых относительных сдвигах исходных М-последовательностей появлялся четвертый уровень корреляционных функций, равный 255 или -257. Сдвиги, при которых появлялся четвертый уровень, назовем аномальными. Исследования показали, что один аномальный сдвиг приходится на 3-4 нормальных сдвига (для взаимно-корреляционных функций, для автокорреляционных - реже). Если при построении ансамбля последовательностей Гоулда такие аномальные сдвиги исходных М-последовательностей не использовать, то корреляционные функции этого ансамбля будут трехуровневыми, а ансамбль будет содержать приблизительно последовательностей (для это приблизительно ).

В табл.3.3 приведены взаимные корреляционные спектры, последовательностей Гоулда на основе предпочтительных троек, которые получены моделированием на ЭВМ.

Таблица 3.3

Рис. 3.17. Максимальные связные множества, образующие предпочтительные тройки (— q=5 – слева на право, — q=13 – справа на лево, —— q=17 – справа налево)

Схему сложения трех М-последовательностей для получения большого ансамбля двоичных сигналов можно использовать при различной длине исходных последовательностей. Большое множество последовательностей Касами получается, если две последовательности имеют длину , - четное, а третья - /12/. Касами показал, что две последовательности длиной должны быть предпочтительной парой , третья последовательность является последовательностью меньшей длины (длина укладывается раз в ). Связь третьей последовательности с первой определяется . Третий полином будет непримитивным, но его номер и восьмеричное представление приводятся в таблицах для длины /10/.

Приведем пример расчета номеров исходных последовательностей для получения последовательностей Касами для :

, .

Значения в таблице /10/ имеются, а - нет. Уточнение значения дает .

Для составим табл.3.4 с примерами исходных последовательностей, дающих большое множество последовательностей Касами.

Таблица 3.4

Предпочтительные пары с выбраны по диаграмме рис. 3.15, а номера третьей последовательности вычислены путем умножения номера первой последовательности на 33 и уточнения полученного значения по методике, приведенной в §3.3.

В отличие от последовательностей Гоулда последовательности Касами имеют пять уровней корреляционной функции: и максимальное значение выбросов корреляционных функций последовательностей Касами не превышает максимального значения для последовательностей Гоулда.

Объем ансамбля последовательностей Касами при равен , a при .

Для ансамбль содержит 32800 последовательностей Касами. В заключение приведем сравнение рассмотренных последовательностей по объему ансамбля и максимальным значениям корреляционных функций для . Сравнительные данные сведены в табл.3.5.

Таблица 3.5

Сравнение М-последовательностей, последовательностей Гоулда и Касами для

3.7. Примеры применения псевдослучайных последовательностей

В заключении следует заметить, что псевдослучайные последовательности нашли применение не только для кодового разделения каналов в системах связи.

По-видимому, раньше всего они начали использоваться для получения псевдослучайного шума в устройствах радиоизмерительной и измерительой техники /19/. Прежде всего это касается М-последовательностей, что обусловлено простотой их генерации.

При увеличении числа разрядов сдвигового регистра m резко возрастает длинна ПСП N=2^m-1. Например, при m=20 формируемая в регистре ПСП повторяется только после прохождения 2²⁰-1 фактически не коррелированных двоичных цифр. Для интервалов наблюдения, более коротких, чем период ПСП N, законы распределения первого и второго порядков, полученные при ее обработке совершенно идентичны аналогичным законам распределения, которые получаются для истинного шумового случайного процесса, формируемого по схеме Бернулли путем независимой выборки результатов действительных случайных испытаний. В этих испытаниях с равной вероятностью появляются величины +а и –а. Сумма S из n<m<<2^m-1 смежных двоичных цифр (0 или 1), принадлежащих ПСП, во всех имеющих практическую значимость случаях обладает биноминальным распределением, характеризующим ситуацию, когда в n независимых испытаниях получается S благоприятных исходов. Таким образом, используя простые счетчики, можно получать случайные числа с биноминальным или (при больших n) примерно гауссовским распределением. Пропуская псевдослучайный сигнал через ФНЧ с постоянной времени значительно превышающей длительность элемента ПСП τ (но не большей значения m·τ), можно получить сигнал, у которого распределение первого порядка совершенно не отличается от гауссовского.

Спектральная плотность мощности псевдослучайного прямоугольного аналогового сигнала является обязательно линейчатой. Расстояние между спектральными линиями обратно пропорционально длительности периода N·τ /16/. Псевдослучайный шум действует совершенно также, как и белый шум с ограниченным спектром, неравномерность которого не превышает 0,1дБ вплоть до частоты 0,2·π·τ. При помощи формирующих фильтров можно легко трансформировать спектр мощности требуемым образом.

Упрощенная функциональная схема генератора псевдослучайного шума приведена на рис. 3.18. Она позволяет получить шум в цифровом виде, бинарный шумовой сигнал с точной фиксацией уровней (положительного и отрицательного), приблизительно гауссовский шум с заданным спектром мощности и шум с заданным распределением амплитуды.

Генераторы псевдослучайных шумовых сигналов обладают несколькими преимуществами по сравнению с аналоговыми: псевдослучайный шумовой сигнал формируется при помощи надежной цифровой схемы; ширина спектра двоичного шумового сигнала пропорциональна частоте тактовых импульсов; сдвиговый регистр может быть возвращен в исходное состояние, что позволяет точно повторять данную реализацию последовательности случайных событий.

В настоящее время существует большое число разнообразных схем генераторов случайных сигналов, основным элементом которых является генератор ПСП (см., например, /20, 21/).

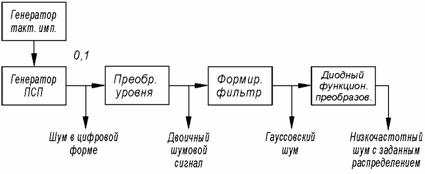
Рис.3.18. Функциональная схема генератора псевдослучайных сигналов

Широкополосные сигналы, полученные на основе ПСП, широко используются для повышения помехоустойчивости и эффективности связи в каналах с многолучевым распространением радиоволн. До изобретения ШПС для этой цели использовались различные методы разнесенного приема /22/, которые относятся к пассивным методам борьбы с замираниями сигналов.

Активные методы предполагают, во-первых, использование сигналов , специально предназначенных для передачи информации по многолучевым каналам, во-вторых, они предполагают получение более полных данных о свойствах и состоянии канала связи и использование этих данных для повышения эффективности системы связи и улучшения ее помехоустойчивости. Данные о состоянии канала получаются на основании изучения параметров принимаемого сигнала. Такое изучение обычно проводится параллельно с приемом информации, а его результаты используются при обработке сигналов.

Применение активных методов возможно только в широкополосных системах связи.

Главным преимуществом ШПС является то, что они дают возможность разделить пришедший в точку приема суммарный многолучевой сигнал на отдельные нефлюктуирующие лучи – сигналы, пришедшие по каждому из лучей распространения. Это достигается применением для обработки сигнала согласованного фильтра, который, как известно, сжимает широкополосные сигналы во времени в базу раз. При этом основные максимумы сигналов отдельных лучей разделяются во времени. Незначительное изменение задержки одного из лучей не приведет к изменению амплитуды суммарного сигнала (после фильтра). Сместится по времени лишь один из максимумов сигнала.

Ширина основного максимума АКФ сигнала, как известно, равна (F – ширина спектра сигнала). Поэтому для разделения лучей с минимальной разностью времени распространения Δτ необходимо использовать сигналы с F>1/Δτ. Такие же результаты можно получить в многоканальном корреляционном устройстве. Для эффективного разделения лучей ШПС должны обладать хорошими автокорреляционными свойствами.

При разделении лучей появляется возможность эффективно использовать энергию всех лучей, т.к. при этом можно осуществить некогерентное их накопление. Впервые на практике это было реализовано в коротковолновой системе связи «Rake» («Грабли») /23/, в которой применены широкополосные дискретные ЧМ сигналы, полученные на основе М-последовательности. В настоящее время это название системы стало нарицательным; rake – процедура используется, как указывалось выше, в системах с кодовым разделением каналов CDMA.

Последовательности Голда и М-последовательности нашли применение для формирования широкополосных сигналов в спутниковых радионавигационных системах (СРНС), в которых последние используются как для передачи различного рода навигационной информации, так и для кодового разделения сигналов различных спутников. Принципы работы СРНС и построения аппаратуры потребителей достаточно подробно освящено в /24/.

3.8. Основная информация

1. В асинхронных адресных системах связи должны использоваться сигналы, удовлетворяющие следующим условиям: сигналы, должны иметь большую базу и большой ансамбль сигналов, «хорошие» корреляционные и взаимные корреляционные функций, а также формироваться с помощью относительно простых схем с быстрой перестройкой на другие сигналы и обрабатываться с помощью не очень сложных устройств в приемнике.

Этим условиям в той или иной степени удовлетворяют сигналы, сформированные на базе двоичных последовательностей с использованием манипуляции по фазе или амплитуде. Наибольшее применение находят фазоманипулированные сложные сигналы. База этих сигналов равна числу элементов в последовательности. Дискретно-частотные сигналы, при формировании которых используется манипуляция по частоте, позволяют получить большую базу при ограниченном числе элементов в сигнале, но имеют небольшой ансамбль.

2. Среди двоичных последовательностей, используемых для формирования сложных фазоманипулированных сигналов, известны ортогональные и квазиортогональные двоичные последовательности. Ортогональные последовательности (Уолша, Хаара, Радемахера и др.) находят ограниченное применение вследствие того, что они имеют ограниченный объем ансамбля, да и ортогональность у них наблюдается только в точке, а при рассогласованиях во времени и частоте они дают большие боковые выбросы.

Среди квазиортогональных последовательностей известны последовательности Лежандра, М-последовательности, нелинейные рекуррентные последовательности и др. Последовательности Лежандра известны для небольшой длины, объем ансамбля их невелик, поэтому они находят пока ограниченное применение. М-последовательности (линейные рекуррентные последовательности) формируются с помощью регистра сдвига, охваченного обратными связями через сумматор по модулю 2, а для формирования нелинейных рекуррентных последовательностей используется нелинейная обратная связь. Нелинейные рекуррентные последовательности образуют очень большой ансамбль сигналов, но пока неизвестны нелинейные рекуррентные последовательности, обладающие «хорошими» корреляционными функциями.

3. Для увеличения объема ансамбля используются составные сигналы, сформированные на базе двух и более ортогональных или квазиортогональных последовательностей. При образовании составных сигналов можно использовать операции либо суммирования по модулю 2, либо мажоритарное правило.

4. Двоичные последовательности, формируемые с помощью регистров сдвига, находят широкое применение в широкополосных системах связи благодаря относительной простоте технической реализации схемы формирования.

5. При выборе обратных связей в регистре сдвига в соответствии с примитивным полиномом генерируются М-последовательности, которые имеют «хорошие» автокорреляционные функции, но малый ансамбль сигналов и большие выбросы взаимных корреляционных функций.

6. Среди всех М-последовательностей одной длины можно найти такие пары, называемые предпочтительными, которые имеют трехуровневые взаимные корреляционные функции, причем максимальный выброс равен .

7. Связные множества состоят из М-последовательностей таких, что каждая пара является предпочтительной, то есть внутри этого множества корреляционные функции являются трехуровневыми и имеют максимальное значение, равное . Но мощность этих множеств (число составляющих их М-последовательностей) небольшая. Для различной длины максимальная мощность принимает значения от 0 до 6.

8. С использованием 2-3 регистров сдвига и сумматора по модулю 2 можно сформировать так называемые последовательности Гоулда и Касами, которые имеют ансамбль значительно больший, чем множество М-последовательностей.

Последовательности Гоулда формируются при использовании регистров сдвига одинаковой длины , то есть при сложении по модулю 2 2-3-х М-последовательностей одинаковой дайны , Объем ансамбля при этом будет равен приблизительно , где -число исходных М-последовательностей (). Трехуровневые корреляционные функции с получаются, если исходные М-последовательности составляют предпочтительную пару, а для случая трех исходных М-последовательностей - предпочтительные тройки, при дополнительном условии выбора нормальных сдвигов М-последовательностей.

9. Последовательности Касами формируются из трех исходных М-последовательностей различной длины: первые две последовательности, составляющие предпочтительную пару с , имеют длину , - четное, а третья последовательность - длину . Последовательности Касами имеют пятиуровневые корреляционные функции, но максимальное их значение не превышает . Объем ансамбля последовательностей Касами равен .

3.9. Вопросы для самопроверки и самостоятельной работы

1. Какие характеристики сигналов являются важнейшими при использовании их при РКФ в ААСС?

2. Какой вид сложных сигналов чаще всего используется в AACС и почему?

3. Как можно упростить процедуру вычисления КФ ФМ сложных сигналов, КФ AM сложных сигналов? Чем будут различаться эти процедуры для ФМ и АМ сложных сигналов?

4. Какие виды сложных сигналов рекомендуется использовать для получения сигналов с большой базой В, если быстродействие используемых МС не позволяет получать непосредственно двоичную последовательность длиной N = В?

5. Что такое линейная рекуррентная последовательность? Какие другие названия этих последовательностей еще известны?

6. Что такое нелинейная рекуррентная последовательность? Какое отличие ее от линейной рекуррентной последовательности по построению схемы формирования, объему ансамбля и корреляционным свойствам?

7. Что такое последовательность Гоулда? Как последовательности Гоулда отличаются от М-последовательностей по схеме формирования, объему ансамбля и корреляционным свойствам?

8. Какое правило может быть использовано при объединения нескольких двоичных последовательностей для формирования производных, составных сигналов?

9.Что такое номер М-последовательности? Существует ля связь между номерами М-последовательностей одинаковой длины?

10. Каковы отличительные положительные качества М-последовательностей? Каковы недостатки М-последовательностей?

11. Почему М-последовательность называется псевдослучайной последовательностью?

12. Сколькими способами можно получить любой циклический сдвиг М-последовательности в виде суммы циклических сдвигов, номера которых меньше степени проверочного полинома? Сколько слагаемых может быть в этих суммах?

13. Какой циклический сдвиг принимается за нулевой? Что имеют общего нулевые циклические сдвиги различных последовательностей?

14. В чем состоит сущность свойства децимации М-последовательности?

15. Оценить порядок отношения максимального бокового выброса к значению главного выброса КФ двух последовательностей, составляющих предпочтительную пару, при большой длине последовательности?

16. При какой степени проверочного полинома можно получить предпочтительные пары?

17. Какие нужно взять М-последовательности, чтобы на их основе сформировать последовательности Гоулда с трехуровневыми КФ? Каким будет максимальный выброс авто- и взаимной корреляционной функций последовательностей Гоулда?

18. Пользуясь рис.3.13, 3.15, ответить на вопрос о максимальном выбросе корреляционных функций для пар последовательностей;. 245-29, 245-5, 245-25.

19. Чем отличаются авто- и взаимные корреляционные функции следующих ансамблей последовательностей: М-последовательности (предпочтительные пары) и последовательности Гоулда на основе двух М-последовательностей (также предпочтительные пары)?

20. Что дает объединение трех М-последовательностей? Чем отличается большое множество последовательностей Касами от последовательностей Гоулда, сформированных на основе трех М-последовательностей (по объему ансамбля, схеме формирования, корреляционным свойствам)?

3.10. Задачи

3.1. По проверочному уравнению записать характеристическое уравнение, определить длину М-последовательности, нарисовать схему ее формирования.

3.2. Записать М-последовательность, формируемую с помощью проверочного полинома , используя проверочное уравнение (3.3). Составить схему формирования М-последовательности и проверить, сформирует ли эта схема полученную последовательность.

З.З. Записать проверочные полиномы степени 5, если их восьмеричные представления 45, 75, 67. Какова длина М-последовательности?

3.4. Убедиться, что полином с восьмеричным представлением 75 имеет номер 3 (номер 1 имеет полином с восьмеричным представлением 45), .

3.5. Записать проверочные полиномы степени 7, если их восьмеричные представления 211, 367, 325. Записать обратные полиномы и представить их в восьмеричном виде. Проверить полученные результаты по таблице приложения 1.

3.6. Сформировать М-последовательность с проверочным полиномом 23. Определить число 0 и I в последовательности. Убедиться, что последовательность содержит все возможные комбинации по символов, кроме нулевой. Чему равно ?

3.7. Представить периодическую корреляционную функцию М-последовательности длиной 7 и 15 на одном рисунке. Как будет меняться КФ при увеличении длины?

3.8. Определить порождающий полином М-последовательности, если проверочный полином a) , б) . По заданному проверочному уравнению сформировать М-последовательность и убедиться, что нулевой ее сдвиг описывается порождающим полиномом.

3.9. По проверочному полиному определить, какой циклический сдвиг дадут суммы по модулю 2 следующих сдвигов: а) нулевого и второго, б) второго и третьего, 3) нулевого и первого, г) нулевого и четвертого. Записать все сдвиги М-последовательности и, суммируя соответствующие сдвиги по модулю 2, убедиться в правильности полученных ответов.

3.10. Проверочный полином М-последовательности . Определить, суммы каких двух циклических сдвигов дадут 6-й циклический сдвиг? Сколькими вариантами сумм из двух циклических сдвигов

можно получить каждый циклический сдвиг для заданной длины последовательности? Для любой длины последовательности? Задачу решить, выписав все циклические сдвиги.

3.11. Для длины 63 какие децимации приведут к образованию последовательностей той же длины?

3.12. Определить требуемое быстродействие микросхем, если требуется сформировать двоичную последовательность длительностью 10 мс. с базой . Какую базу можно реализовать при использовании МС серии 564, 133,106?

3.13. Для М-последовательности с проверочным полиномом определить последовательность, образованную в результате децимаций по индексу 3. Определить номер полученной последовательности, ее проверочный полином (по табл. приложения 1). Провести проверку, используя понятие нулевого сдвига.

3.14. Определить предпочтительные пары, для проверочных полиномов степени : а) , б) , в) , г) , д) .

3.15. Определить исходные последовательности (номера и их полиномы) для образования большого множества последовательностей Касами длиной 63. Чему равен объем ансамбля? Составить схему формирования последовательностей Касами, используя полученные проверочные полиномы.

Ответы на задачи

1 раздел

1.1. а) , б) . 1.2. В 3 раза уменьшается. 1.3. При ЧРК 40 МГц, при ВРК - 8 МГц (ИКМ), 2 - 4 МГц (дельта-модуляция). 1.4. 10 телеграфных каналов. 1.5. а) 6,9, б) 13,8, в) 7,6, 3,8, 2,5. 1.6. а) , б) , в) , , . 1.7. а) 1, 1, 2, 5, 10. б) многопозиционное кодирование, так как каждым сигналом передается дв. ед. информации. 1.8. 69, 138, 25. Комбинационное разделение потребует в 5,5 раз или в 2,76 раз меньше средней мощности передатчика, но источники должны быть синхронными и работать на одинаковых или кратных скоростях. 1.9. а) при любом сообщение не искажается, б) 1.11 б) .

2 раздел

2.1. Либо мощность увеличить в 2 раза и перейти на противоположные сигналы (синхросигнал передается параллельно с информационным), либо полосу частот увеличить в 2 раза. 2.2. Противоположные сигналы - ka=200, ортогональные сигналы ka=210. 2.3. или . 2.4. Уровни внутрисистемных помех и внутренних шумов должны быть одинаковыми. 2.5. Увеличится вероятность ошибки в 2 раза, ka=40 или . 2.6. . 2.7. . 2.8. а) , б) . 2.9. . 2.10. . 2.11. а) , б) .

3 раздел

3.1. 1011, 7. 3.2. 1010011. 3.3. 100101, 111101, 110111, 31. 3.5. 10001001, 11110111, 11010101, 221, 357, 253. 3.6. 4,8. 3.8. а) , б) . 3.9. а) 3, б) 0, в) 5, г) 6. 3.10. С6=С4+С0=С5+С3=С2+С1, 3, (N-1)/2. 3.11. 1,2,4,8,16,32, 5,10,20,40, 17,34,11,22,44, 25,50,37, 13,26, 52,19,38,41, 23,46,29,58,53,43. 3.12. нс. 3.13. 3,1101. 3.14. а) 1,3,7,15; б) 11,31,5,23; в)1,3,27,13, 39,47,7,5,15,43; г) 17,55,61,187,45,3; д) 103,125,1,149,91,119,61,83, 35,175,49,479. 3.15. 5,11,35; 147,155,013.

Список литературы

1. Бессарбова А.А., Клыков М.В. О свойстве сдвига и сложения М-последовательностей. – Радиотехника, 1984, т.39, №3.

2. Варакин Л.Е. Теория систем сигналов. – М.: Советское радио, 1970. – 376 с.

3. Венедиктов М.Д., Марков В.В., Эйдус Г.С. Асинхронные адресные системы связи. – М.: Связь, 1968. – 271 с.

4. Диксон Р.К. Широкополосные системы: Пер. с англ. / Под ред. В.И. Журавлева. – М.: Связь, 1979. – 304с.

5. Кловский Д.Д. Теория передачи сигналов. – М.: Связь, 1973. – 376 с.

6. Скляр Б. Цифровая связь: Пер. с англ. /под ред. А.В. Назаренко. – М.: Вильямс, 2004. – 1104 с.

7. Многостанционный доступ в спутниковых системах связи / Венедиктов М.Д., Даниэлян С.А., Марков В.В., Эйдус Г.С. – М.: Связь, 1973. – 97 с.

8. Немировский М.С. Цифровая передача информации в радиосвязи. М.: Связь, 1980. - 256 с.

9. Пенин П.И. Системы передачи цифровой информации. - М.: Советское радио, 1976. - 368 с.

10. Питерсон У. Коды, исправляющие ошибки: Пер. с англ./Под ред, Р.Л. Добрушина. - М.: Мир, 1964. - 338 с.

11. Радиосистемы передачи информации / Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В,А, - М,: Радио и связь, 1982. - 264 с.

12. Сарвате Д.В., Персли М.Б. Взаимнокорреляционные свойства псевдослучайных и родственных последовательностей. - ТИИЭР, I980, т.68, № 5, с.59-90.

13. Сикарев А.А., Лебедев О.Н. Микроэлектронные устройства формирования и обработки сложных сигналов. - М.: Радио и связь, 1983. - 216 с.

14. Спилкер Дж. Цифровая спутниковая связь: Пер. с англ. /Под ред, В.В.Маркова. - М.: Связь, 1976. - 592 с.

15. Теория передачи сигналов /Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. - М.: Связь, 1980. - 288 с.

16. Тузов Г.И. Статистическая теория приема сложных сигналов. - М.: Советское радио, 1977. - 400 с.

17. Цифровые методы в космической связи /Под ред. С.У. Голомба /Пер с англ. /Под ред. В.И. Шляпоберского. - М.: Связь, 1969. - 271 с.

18. Шумоподобные сигналы в системах передачи информации /Под ред В.Б. Пестрякова. - М.: Советское радио, 1973. - 424 с.

19. Корн Г. Моделирование случайных процессов на аналоговых и аналогово-цифровых машинах: Пер. с англ./ под ред. Е.В. Доброва. – М.: Мир, 1968. – 315 с.

20. Патент РФ №2208288, 10.08.03; Н 03 В 29/00, G 06 F 7/58.

21. Патент РФ № 2205495, 10.07.03; Н 03 В 29/00.

22. Финк Л.М. Теория передачи дискретных сообщений. – М.: Совю радио, 1970. – 102 с.

23. Петрович Н.Т. Размахнин М.К. – М.: Сов. Радио, 1969. – 230 с.

24. Радиотехнические системы / Ю.П. Гришин, В.П. Ипатов и др; Под ред. Ю.М. Казаринова. – М.: Высш. шк., 1990. – 496 с.