7.1. Требования к АКФ: дополнительный экскурс
7.2. Сигналы с непрерывной частотной модуляцией
7.1. Требования к АКФ: дополнительный экскурс
Вернемся к задачам измерения запаздывания (синхронизации) и разрешения по времени. Принципиальное условие, которое должно выполняться в обеих этих задачах, состоит в использовании сигналов, длительность T которых значительно превосходит время корреляции 
. Большая длительность обеспечивает возможность вложения в сигнал энергии, диктуемой необходимым отношением сигнал-шум, без увеличения пиковой мощности, как правило, жестко лимитированной сверху. В свою очередь, малое время корреляции позволяет осуществить временную компрессию сигнала в согласованном фильтре, а значит, позволяет осуществить измерение запаздывания с высокой точностью и качественное разрешение по времени сигналов, перекрывающихся на входе фильтра. Поскольку 
, то достижение «остроты» АКФ сигнала при 
возможно лишь при большом значении выигрыша от обработки 
, т.е. привлечении широкополосной технологии.
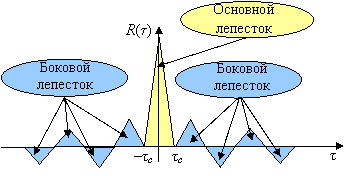
Уточним, какого рода АКФ можно считать «острой» или «хорошей» в контексте рассматриваемых задач приема. Нетрудно показать, что АКФ любого реализуемого сигнала не может в точности равняться нулю вне отрезка 
, если время корреляции меньше длительности сигнала 
. Таким образом, наряду с так называемым основным лепестком или центральным пиком, сосредоточенным внутри отрезка , АКФ будет иметь и боковые лепестки, находящиеся за его пределами (см. рисунок).
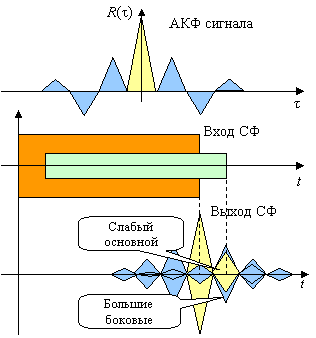
Присутствие боковых лепестков имеет преимущественно вредные последствия как при измерении запаздывания, так и при разрешении по времени. Действительно, оптимальная (МП) оценка запаздывания сигнала предполагает фиксацию временного положения максимума огибающей 
на выходе согласованного фильтра, а огибающая АКФ по форме повторяет отклик цепочки согласованный фильтр–детектор на незашумленный сигнал. В реальной ситуации зашумленных наблюдений всегда имеется вероятность возникновения такого ложного максимума вне «тела» основного пика АКФ, который может превзойти истинный, а значит, привести к аномальной ошибке измерения.
При временном разрешении суперпозиции двух сдвинутых во времени копий радиосигнала с разными амплитудами основной лепесток более слабой копии может оказаться полностью спрятанным под боковым лепестком сильной (см. рисунок). Сценарий такого рода дает характерный пример неразрешенных сигналов, хотя основной лепесток АКФ значительно уже длительности самого сигнала.
Суммируя сказанное, можно в следующей, наиболее общей редакции сформулировать требования к широкополосным сигналам со стороны задач измерения запаздывания и временнóго разрешения: АКФ сигнала должна иметь достаточно острый центральный пик и по возможности низкий уровень боковых лепестков. В следующих разделах главы обсуждаются пути и инструменты достижения этой фундаментальной цели.
7.2. Сигналы с непрерывной частотной модуляцией
Исторически одним из первых найденных сигналов, для которых осуществимо временнóе сжатие согласованным фильтром, оказался импульсный сигнал с линейной частотной модуляцией (ЛЧМ). Как следует из названия, мгновенная частота такого сигнала линейно изменяется в течение его длительности. Рассмотрим радиосигнал, мгновенная частота 
которого возрастает со временем по закону
,
где 
– девиация, т.е. полный диапазон изменения частоты, а 
– как обычно, центральная частота. Полная мгновенная фаза 
сигнала является интегралом от мгновенной частоты и, следовательно, фаза ЛЧМ импульса описывается квадратичным законом
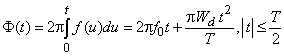
При прямоугольной действительной огибающей комплексная огибающая ЛЧМ сигнала имеет вид
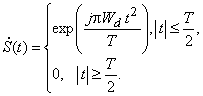
Подставляя последнее соотношение в выражение для АКФ, ее можно найти формально без особых затруднений. Однако менее формальная и весьма прозрачная физически логика позволяет прийти к нужному итогу быстрее.
Из теории частотной модуляции хорошо известно, что когда индекс модуляции 
достаточно велик (
), спектр частотно-модулированного колебания содержит компоненты всех мгновенных частот, причем его форма приближается к действительной огибающей сигнала. Таким образом, в нашем случае спектр располагается в диапазоне 
и имеет форму, близкую к прямоугольной (см. рисунок ниже). Теперь АКФ может быть найдена обратным преобразованием Фурье. Так как энергетический спектр сигнала прямоуголен, его обратное преобразование Фурье оказывается функцией вида 
, так что нормированная комплексная огибающая АКФ ЛЧМ сигнала представима в виде
,
что иллюстрируется рисунок.
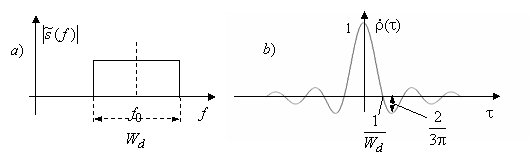
Как следует из рисунка, полная (т.е. измеренная между двумя ближайшими к началу координат нулями) ширина основного лепестка АКФ составляет 
. Условно можно принять ширину основного лепестка на некотором ненулевом уровне равной 
, придя к выводу, что согласованный фильтр осуществляет временную компрессию ЛЧМ сигнала в 
раз.
Пример 7.2.1. ЛЧМ импульс с девиацией частоты 
МГц и длительности 
мкс характеризуется выигрышем от обработки 
и временной компрессией согласованным фильтром примерно в 100 раз.
Вместе с тем ЛЧМ сигнал обладает и рядом серьезных недостатков:
1. Серьезным недостатком ЛЧМ сигнала являются заметные боковые лепестки АКФ. Ближайший из них к началу координат имеет уровень по отношению к основному 
(–13,5 дБ), который не зависит от выигрыша от обработки 
, т.е. не может быть уменьшен увеличением девиации 
. Существуют эффективные методы снижения боковых лепестков с помощью сглаживания огибающей сигнала либо применения специальных взвешивающих окон, иначе говоря, рассогласованной обработки в приемнике. При этом выигрыш в уровне боковых лепестков достигается в обмен на расширение основного пика и/или потери в отношении сигнал-шум.
2. Другой изъян ЛЧМ сигнала – гребнеобразная форма ФН 
. Для одновременного измерения запаздывания и частоты так же, как и для частотно-временного разрешения, наилучшей является игольчатая функция неопределенности, имеющая единственный центральный пик в начале координат и резко спадающая во всех направлениях частотно-временной плоскости.
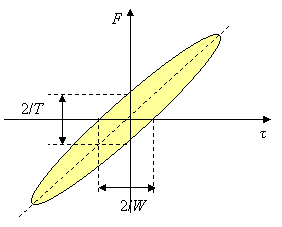
Как следует из рисунка, представляющего пример диаграммы неопределенности ЛЧМ сигнала, последний не может служить эффективным инструментом в решении упомянутых задач. Когда пара значений 
попадает в эллипс диаграммы направленности, точность оценивания названных параметров резко падает, поскольку копии сигнала со всеми подобными парами имеют высокую корреляцию, т.е. трудноразличимы. То же самое справедливо и в части разрешения подобных расстроенных по времени и частоте копий: высокая степень сходства делает задачу их разделения весьма проблематичной.
Непрерывные ЛЧМ сигналы и их модификации до настоящего времени весьма распространены в разнообразных широкополосных системах радио- и гидролокации. В современных же коммерческих телекоммуникациях или общедоступных системах дальней навигации они не находят широкого применения, отдавая приоритетные позиции дискретным сигналам.
7.3. Критерии хорошей апериодической АКФ АФМ сигналов
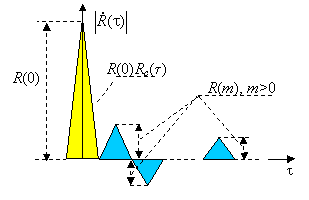
Вспомним, что АКФ 
АФМ сигнала сама оказывается АФМ сигналом, чипом которого служит АКФ 
исходного чипа, а кодовой последовательностью – АКФ 
исходного кода 
. Подобная конструкция явно свидетельствует, что при заданном чипе профиль полной АКФ полностью определяется АКФ кода. В частности, если длительность чипа не превышает периода следования чипов 
, «высота» 
любого бокового лепестка в точке 
просто повторяет значение АКФ кода 
при сдвиге на 
позиций (см. рисунок слева). Следовательно, минимизация уровня боковых лепестков АКФ является наивысшим приоритетом при конструировании сигналов всякий раз, когда в задачи системы входят измерение запаздывания или временное разрешение. Разумеется, в идеале хотелось бы, чтобы все боковые лепестки имели нулевой уровень, однако это абсолютно невозможно для апериодических (импульсных) АФМ сигналов.
Действительно, для АФМ сигнала конечной длины 
и 
, тогда крайний правый боковой лепесток нормированной апериодической АКФ кода будет
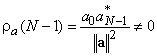
Этот результат напрямую оправдывает ориентацию на минимаксный критерий синтеза сигналов, предписывающий стремиться к минимизации уровня максимального из боковых лепестков АКФ апериодического кода. Формально задача формулируется как
.
В свете данного критерия предпочтительны кодовые последовательности с наименьшим максимальным боковым лепестком, однако подобное требование всегда сопровождается ограничением на метод модуляции или, более конкретно, на алфавит кода, которому принадлежат символы последовательности. Тогда требования к наилучшему сигналу можно оформить как следующую оптимизационную задачу: на множестве всех возможных последовательностей длины N с символами из заранее оговоренного алфавита найти последовательность (или последовательности) с минимальной величиной максимального бокового лепестка апериодической АКФ.
7.4. Оптимизация апериодических ФМ сигналов
Сформулированная выше оптимизационная задача, подобно многим задачам дискретной оптимизации, не имеет какого-либо общего аналитического решения, и типичным подходом к ней является полный перебор. Ограничимся классом ФМ сигналов, нередко признаваемых наиболее привлекательными.
Для любого ФМ сигнала 
, так что 
, и крайний правый боковой лепесток апериодической АКФ 
. Таким образом, для максимального бокового лепестка АКФ апериодического ФМ сигнала справедлива нижняя граница
.
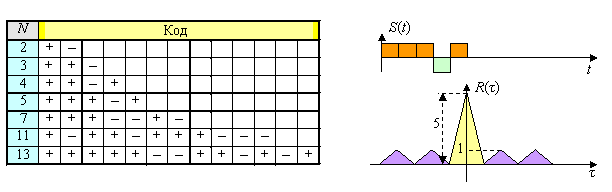
ФМ сигналы, достигающие данной границы, безусловно, оптимальны в свете минимаксного критерия. В литературе они обычно фигурируют под названием кодов Баркера по имени одного из первых их исследователей. Фактически Баркер описал оптимальные бинарные коды, лежащие на данной границе. Традиционно бинарные последовательности символов 
считаются особо привлекательными, поскольку их алфавит в наибольшей степени согласуется с цифровой элементной базой, минимизируя сложность формирования и обработки. В следующей таблице приведены все бинарные коды Баркера. АКФ дискретного сигнала, манипулированного кодом Баркера длины 
, представлена на рисунке ниже.
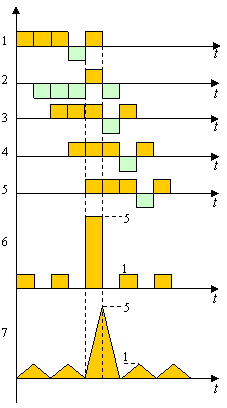
Проиллюстрируем вкратце процедуру согласованной фильтрации сигнала Баркера, прибегнув к конкретному примеру.
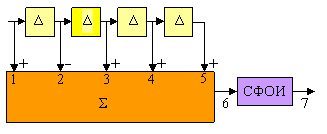
Пример 7.4.1. На рисунке показана структура согласованного фильтра для сигнала Баркера длины 
. Первый ее блок – линия задержки с отводами, шаг которых равен периоду следования чипов 
. Сигналы с отводов подаются на сумматор с весами, последовательность которых зеркальна по отношению к коду. Вторым блоком схемы служит фильтр, согласованный с одиночным чипом (СФОИ). На рисунке справа представлены осциллограммы, пронумерованные соответственно точкам схемы и воспроизводящие подробности согласованной фильтрации видеосигнала Баркера с прямоугольными чипами. Когда последний чип сигнала приходит на вход фильтра, все предшествующие чипы появляются на входах сумматора в положительной полярности и суммируются в фазе, генерируя главный пик АКФ. До и после этого момента на выходе фильтра наблюдаются боковые лепестки
К сожалению, бинарные коды Баркера существуют только для длин, перечисленных в вышеприведенной таблице. Еще в начале 60-х годов Турин и Сторер доказали их несуществование для любых иных нечетных длин и для четных, по крайней мере, в диапазоне 
. Согласно последним публикациям верхняя граница отодвинута до 1 898 884, и вероятность существования бинарных кодов Баркера четной длины вне этого диапазона крайне мала. Значительные усилия неоднократно предпринимались по поиску небинарных ФМ кодов Баркера с эквидистантным фазовым алфавитом (многофазные или М-ичные ФМ коды), однако достигнутые на этом пути результаты пока далеки от обнадеживающих. Оказалось, что даже весьма скромный прирост длины можно получить только в обмен на значительное увеличение объема 
фазового алфавита. Например, небинарный код Баркера длины 
требует, по меньшей мере, 
эквидистантных значений фазы. Большой размер алфавита неизбежно сопряжен с серьезными усложнениями аппаратной реализации, а также резким ужесточением требований к допустимым реализационным погрешностям, дрейфу параметров и т.п.
Существование кодов Баркера только малой длины подталкивает к поиску приемлемых бинарных последовательностей большей длины с уровнем боковых лепестков выше границы для 
. Поскольку ненормированная АКФ любой бинарной последовательности есть сумма слагаемых , возможные значения для «небаркеровких» кодов принадлежат множеству 
. Гарантию нахождения глобально оптимального (т.е. имеющего минимально возможное значение 
при заданном ) бинарного кода может обеспечить лишь полный перебор всех возможных кодов. К сожалению, вычислительный ресурс, необходимый для подобной оптимизации, экспоненциально возрастает с увеличением длины и выходит за грань реальности при длинах больше 50.
По этой причине популярной становится стратегия поиска бинарных кодов с приемлемо малым – без гарантии глобальной оптимальности уровнем апериодического бокового лепестка . Общая идея алгоритма решения такой задачи сводится к предварительному отбору некоторого достаточно узкого подмножества последовательностей, в котором подозревается наличие кодов с подходящими корреляционными свойствами, и последующему полному перебору, минимизирующему только в пределах отобранного подмножества. Одним из примеров подобной стратегии является поход, основанный на соотношении, которое связывает апериодическую АКФ с периодической:
,
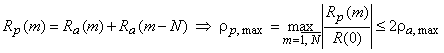где через 
обозначен максимальный боковой лепесток периодической АКФ кодовой последовательности. Откуда непосредственно следует, что
.
Последнее неравенство позволяет сделать весьма примечательный вывод: необходимым условием «хорошей» апериодической АКФ является хорошая (имеющая малый максимальный боковой лепесток ) периодическая АКФ. Иначе говоря, последовательности с хорошей апериодической АКФ могут быть найдены только среди последовательностей с хорошей периодической АКФ. Как будет показано позднее, существуют достаточно продуктивные аналитические инструменты построения последовательностей с хорошими периодическими АКФ. Эта возможность закрепляет за периодической АКФ приоритетную роль в синтезе последовательностей с приемлемыми корреляционными свойствами и оправдывает акцент следующего раздела на изучении свойств периодической АКФ.