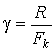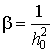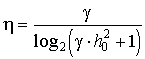1. Задачи приемного устройства

2. Статистические критерии оптимального приема дискретных сигналов

3. Отношение правдоподобия

4. Оптимальный приемник полностью известных сигналов

5. Оптимальный приемник известных сигналов с пассивной паузой

6. Оптимальный приемник известных сигналов с активной паузой

7. Вероятность ошибки в оптимальном приемнике

8. Потенциальная помехоустойчивость различных видов дискретной модуляции

9. Оптимальная фильтрация дискретных сигналов

10. Прием дискретных сигналов с неизвестной фазой

11. Прием сигналов ОФМ

12. Прием дискретных сигналов со случайной амплитудой

14. Мера количества информации в дискретном сообщении

15. Энтропия дискретного источника с независимым выбором сообщений

16. Энтропия дискретного источника с зависимыми сообщениями

17. Избыточность источника

18. Производительность источника

19. Совместная энтропия двух источников

20. Взаимная информация источников сообщений

21. Скорость передачи и пропускная способность канала связи

22. Статистическое кодирование дискретных сообщений

23. Статистическое кодирование кодовых слов

24. Пропускная способность однородного симметричного канала связи

25. Энтропия непрерывной случайной величины и её свойства

26. Энтропия и производительность эргодического источника непрерывного сигнала

27. Пропускная способность непрерывного канала связи

28. Эпсилон-энтропия источника непрерывных сообщений

29. Обмен мощности сигнала на ширину его спектра

30. Сравнение пропускной способности непрерывного и дискретного каналов связи

31. Эффективность систем связи

1. Задачи приемного устройства

На вход приемного устройства (приемника) любой системы связи обычно поступает смесь переданного сигнала S(t) и помехи n(t)

x(t) = S(t) + n(t), (1.1)

причем сигнал S(t) представляет собой, как правило, сложное колебание, содержащее, кроме времени t , множество параметров (амплитуду, фазу, частоту и пр.) S(t) = f(a, b, c, ... t).

Один или группа этих параметров используется для передачи информации, а задачей приемника является определение (измерение) этих параметров в условиях мешающего действия помех.

Если для решения своей задачи приемник использует все параметры сигнала, не несущие информацию, то он называется приемником полностью известного сигнала.

Если эта задача решается наилучшим образом, по сравнению с другими приемниками, то такой приемник называется оптимальным или приемником, реализующим потенциальную помехоустойчивость ("идеальный" приемник).

Потенциальная помехоустойчивость впервые была определена в 1946г. выдающимся советским ученым В.А.Котельниковым в условиях гауссовских помех. Согласно теории потенциальной помехоустойчивости любая система передачи информации с заданным ансамблем сигналов в условиях конкретных помех имеет предельную помехоустойчивость, которая не может быть улучшена путем совершенствования приемника и поэтому называется потенциальной помехоустойчивостью.

Если для определения информационного параметра используются не все параметры сигнала ,не несущие информацию, то это приемник неполностью известного сигнала. Такой приемник также может быть оптимальным (лучшим среди этого класса приемников), но его помехоустойчивость всегда ниже потенциальной.

В зависимости от назначения системы связи задачи приемника классифицируются следующим образом.

1. Обнаружение сигнала. При этом приемник решает, есть на его входе сигнал (вместе с помехой), или же на его входе имеется только одна помеха. Сам сигнал заранее известен.

На рис. 1.1 в некотором пространстве (система координат 1, 2) изображен вектор сигнала S, на который накладываются векторы помех с различными фазами и амплитудами (в любой момент времени к вектору сигнала добавляется один из векторов помех; на рисунке изображено несколько векторов помех, чтобы показать, что вектор помехи может иметь любую фазу и величину). Если сигнал S на входе приемника отсутствует, векторы помех исходят из начала координат (точка 0).

Для решения вопроса о наличии или отсутствии сигнала на входе приемника, все пространство разбивается на два подпространства: подпространство сигнала и подпространство помех. В зависимости от того, в какое подпространство попадает конец результирующего вектора, приемник выполнит решение о наличии или отсутствии сигнала на его входе.

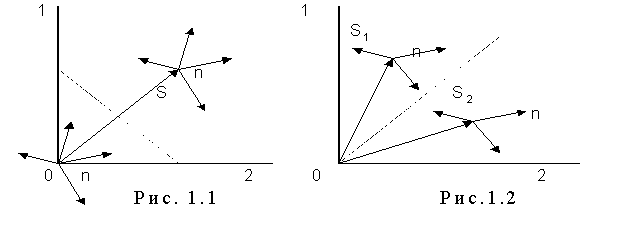
Граница подпространств (на рис.1.1 и 1.2 показана пунктиром) зависит от критерия верности, используемого при приеме. Если под действием помехи конец суммарного вектора попадает в подпространство помех, имеет место пропуск сигнала; если, наоборот, конец вектора помехи без сигнала попадает в подпространство сигнала, имеет место ложная тревога.

2. Различение двух сигналов (или m сигналов). Приемник решает, какой из сигналов (S1 или S2) имеется на его входе; на рис.1.2 показаны два вектора сигналов вместе с помехами. Все пространство сигналов и помех разбивается на подпространства по числу сигналов( в данном случае на два подпространства); приемник принимает решение в пользу того сигнала, в подпространстве которого находится конец вектора суммы сигнала и помехи. Если под действием помехи конец суммарного вектора попадет в чужое подпространство, произойдет ошибка.

Следует иметь в виду, что, когда приемник предназначен для приема дискретных сигналов (обнаружение сигналов, различение сигналов), то, как правило, форма выходных сигналов не совпадает с формой сигналов на его входе. Например, если приемник осуществляет различение сигналов S1(t) = A×cosw1t и S2(t) = A×cosw2t (дискретная частотная модуляция), то при приеме сигнала S1(t) на выходе приемника будет импульс напряжения положительной полярности, а при приеме сигнала S2(t) - импульс отрицательной полярности (или 0, в зависимости от конкретной реализации схемы приемника).

3. Оценка параметров сигнала - например, его амплитуды или величины запаздывания, применяется в телеметрических системах, в радиолокации; при этом скорость изменения измеряемого параметра сигнала значительно меньше скорости измерения (значение параметра не изменяется в процессе измерения).

4. Восстановление формы передаваемого сигнала осуществляется при приеме аналоговых сигналов (фильтрация) и отличается от оценки параметра тем, что измеряемый параметр непрерывно меняется в процессе измерения.

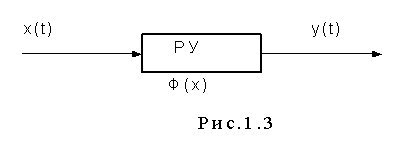
Таким образом, приемник представляет собой решающее устройство (рис.1.3), которое в соответствии с некоторым правилом Ф(х), (правило решения), определяет значение информационного параметра (принимает решение о значении выходного сигнала y(t), используя входной сигнал x(t)).

2. Статистические критерии оптимального приема дискретных сигналов

Количественно помехоустойчивость определяется некоторой мерой соответствия принятого сообщения (сигнала) переданному. Эта мера (мера качества решения) из-за случайного характера помех всегда является статистической и определяется потребителем сообщения (степенью чувствительности потребителя к тем или иным искажениям).

Оптимальный приемник (оптимальное правило решения) обеспечивает наилучшее качество решения, то есть обеспечивает минимум искажений переданного сообщения в соответствии с мерой качества, заданной потребителем. Оптимальное значение меры качества, которое достигается приемником в процессе оптимизации, называется критерием оптимальности приема (или просто критерием качества).

При приеме дискретных сигналов в качестве меры помехоустойчивости обычно используется средний риск Rср, тогда критерием оптимальности является min {Rср};

Rср = 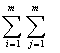Пij P (Si , yj), (2.1)

где P (Si , yj) - совмеcтная вероятность передачи S i и приема yj ;

Пij - функция потерь (риск потребителя) при приеме yj , когда передавался сигнал Si ; при этом i = j соответствует правильному приему (значения Пij =0), i ¹ j - ошибка (значения Пij > 0) ;

m - число передаваемых сигналов.

Приемник, работающий по этому критерию, называется байесовским, а правило решения - байесовским правилом.

Рассмотрим некоторые наиболее часто применяемые критерии при передаче двух сигналов S1(t) и S2(t), так как в технике связи такая задача встречается наиболее часто.

При различении сигналов обязательно возникают ошибки при любой мощности сигнала и помехи, так как из-за случайного характера помех возможны выбросы помехи значительной величины. На рис.2.1 приведен граф переходов в системе связи, когда передаются сигналы S1(t) и S2(t). Если передавался сигнал S1, а принят y1 - это означает, что первый сигнал принят правильно. Если же передавался сигнал S1, а принят у2 - это означает, что при приеме вместо первого сигнала получен второй сигнал - произошла ошибка.

Условные вероятности Р(у1/S1) и Р(у2/S2) есть вероятности правильного приема этих сигналов.

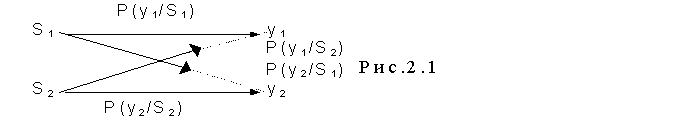
Существует несколько критериев помехоустойчивости при различении сигналов. Эти критерии фактически отличаются правилом решения, которые определяют положение границы подпространств (пунктир на рис.1.2), исходя из конкретных требований потребителя к качеству приема сигналов различного назначения.

1. Критерий минимального среднего риска.

Согласно (2.1) этот критерий для двух сигналов минимизирует средний риск

Rср = {П12Р(S1,y2) + П21Р(S2,y1) = П12Р(S1)Р(y2/S1) + П21Р(S2)Р(y1/S2) . (2.2)

В зависимости от значения функции потерь (в данном случае весовых коэффициентов П12 и П21) этот критерий может применяться в системах связи различного назначения с учетом тех потерь (или убытков), которые являются следствием искажения сигналов S1 и S2.

Например, если сигнал S1 - отсутствие тревоги, а S2 - сигнал тревоги (пожарная или охранная сигнализация), то Р(у2/S1) - это вероятность ложной тревоги, а Р(у1/S2) - вероятность пропуска сигнала тревоги. Если это система противопожарной сигнализации, то в результате ложной тревоги убытки составляют, например, 10 рублей (затраты на ложный выезд), а в результате пропуска тревоги (в результате чего может сгореть важный объект) убытки составляют миллион рублей. В этом случае весовые коэффициенты могут быть соответственно равны П12 =10, П21 = 106. Приемник должен принимать решение таким образом, чтобы получить min{Rср}. Очевидно, для этой цели границу подпространств (рис.1.2) целесообразно удалить от сигнала тревоги S2 за счет увеличения вероятности искажения сигнала S1, при этом уменьшится вероятность пропуска сигнала тревоги; в результате критерий min{Rср} обеспечит минимальные убытки системы противопожарной безопасности.

2. Критерий максимального правдоподобия (критерий МП).

Критерий МП получается из критерия минимального среднего риска, если принять, что П12 = 1/P(S1), П21 = 1/P(S2).

При этом оптимальный приемник принимает решение таким образом, что минимизируется значение

l п = P(y2/S1) + P(y1/S2) . (2.3)

Критерий МП иногда называется критерием минимума потерь информации, так как оптимальное правило решения в этом случае устанавливает границу подпространства (рис.1.2) так, чтобы уменьшить вероятность искажения того сигнала, вероятность передачи которого меньше (следовательно, этот сигнал содержит больше информации).

Критерий МП применяется в системах связи также в тех случаях, когда априорные вероятности Р(S1) и P(S2) неизвестны.

3. Критерий идеального наблюдателя.

Если весовые коэффициенты П12 = П21 =1, то критерий минимального среднего риска минимизирует среднюю вероятность ошибки

pош = P(S1)P(y2/S1) + P(S2)P(y1/S2) (2.4) и называется критерием идеального наблюдателя.

Критерий идеального наблюдателя широко применяется в системах связи, когда искажения любого сигнала одинаково нежелательны и совпадает с критерием МП, если вероятности Р(S1) = P(S2) = 0,5.

4. Критерий Неймана-Пирсона.

В некоторых системах передачи информации (системах радиолокации, некоторых системах сигнализации) имеется необходимость фиксирования (задания) одной из условных вероятностей Р(у1/S2) или Р(у2/S1). При этом оптимальный приемник принимает решение таким образом, чтобы минимизировать ту условную вероятность, которая не задана. Критерий оптимальности, который используется таким приемником называется критерием
Неймана-Пирсона.

Например, задана вероятность пропуска сигнала S1 , то есть Р(у2/S1) = a.. Тогда критерий Неймана-Пирсона требует минимизации условной вероятности Р(у1/S2), обеспечивая заданное значение a. Вероятность Р(у1/S2) обычно обозначается b, тогда (1-b) = Р(у2/S2) называется качеством решения. Правило решения Неймана-Пирсона обеспечивает (min b) или мах(1- b) при a = const.

Приемник при использовании критерия Неймана-Пирсона строится таким образом, чтобы получить достаточно малую вероятность пропуска cигнала(цели ) Р(у2/S1)=a.. С тем, что при этом может (несмотря на минимизацию b=Р(у1/S2)) оказаться много ложных тревог, приходится мириться. В этом и заключается сущность данного критерия.

3. Отношение правдоподобия

Различение сигналов в приемном устройстве обычно осуществляют путем установления некоторого "порога" на выходе приемника, фактически играющего роль "границы подпространств" сигналов S1 и S2.

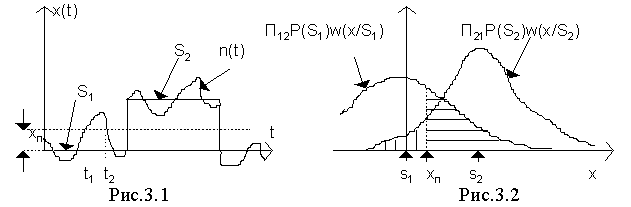
На рис. 3.1. приведен некоторый дискретный сигнал х(t) (импульсы постоянного тока), на который накладывается флюктуационная помеха и проведена пунктирная линия, соответствующая выбранному порогу хп.

Если величина x(t) < xп , приемник выдает сигнал S1, если же x(t) > xп , приемник выдает сигнал S2. Как видно из рисунка, на отрезке времени t1, t2 под действием сильной помехи величина х > xп , т. е. в этом случае приемник может выдать сигнал S2 , хотя передавался S1.

Различные критерии приема дискретных сигналов фактически отличаются способом установления величины порога. Данная задача проще всего решается с помощью "отношения правдоподобия". Для рассмотрения этого вопроса обратимся к рис. 3. 2.

Если бы на входе приемника отсутствовали помехи, мы имели бы дело с "чистыми" сигналами S1 и S2 и задача разделения сигналов была бы очень проста. При наличии же помех сигналы искажаются и для их описания приходится использовать вероятностное пространство. Сами сигналы вместе с помехами описываются уже функциями плотности вероятности w(x/S1) и w(x/S2), которые изображены на рис. 3.2. (эти функции умножены также на весовые коэффициенты П12Р(S1) и П21Р(S2)). На этом же рисунке показан порог хп.

Заштрихованная часть рисунка левее хп имеет площадь, равную

П21Р(S2)w(x/S2)dx = П21Р(S2)P(x/S2), (3.1)

а заштрихованная часть правее хп имеет площадь, равную

П12Р(S1)w(x/S1)dx = П12Р(S1)P(x/S1), (3.2)

Сумма этих величин, в соответствии с формулой (2.1), есть средний риск Rср. Из рис. 3.2. видно, что Rср будет минимальным, когда минимальна суммарная площадь под кривыми. Это будет в том случае, если величина хп соответствует точке пересечения кривых на рис. 3.2. Следовательно, условием получения min{Rср} является такой порог хп, при котором наступает равенство ординат приведенных кривых, т. е.

П12Р(S1)w(x/S1)dx = П21Р(S2)w(x/S2), (3.3)

откуда получаем следующее соотношение:

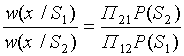. (3.4)

Стоящее слева выражение называется отношением правдоподобия

l(х) = 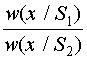, (3.5)

а w(x/S i), которая представляет собой плотность вероятности того, что принятый сигнал х образовался при передаче сигнала Si , обычно называется функцией правдоподобия (функцией правдоподобия является также любая монотонная функция от w(x/Si), например log[ w(x/Si)]).

Чем больше значение w(x/S i), тем более вероятно, что х содержит сигнал Si (это очевидно из рис. 3.2). Справа стоящее выражение называется пороговым отношением правдоподобия

l0 = 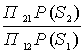. (3.6)

Приемник, использующий отношение правдоподобия, работает следующим образом.

1. Анализируя поступающий на его вход сигнал, вычисляет отношение правдоподобия l(х).

2. По известным значениям априорных вероятностей Р(S1) и P(S2), а также заданным весовым коэффициентом П21 и П12, вычисляется пороговое отношение правдоподобия l0.

3. Величина l(х) сравнивается с l0,

если l(х) > l0, приемник выдает сигнал S1, в противном случае сигнал S2 . (3.7)

Выражение (3.7) является правилом решения Ф(х) решающего устройства, показанного на рис.1.3.

Правило решения (3.7) является общим для двоичных систем связи, использующих любой критерий оптимального приема ; отличие только в значении порога l0 .

Если приемник работает по критерию минимального среднего риска, величина l0 определяется формулой (3.6).

Для критерия идеального наблюдателя, в этой формуле коэффициенты

П12 = П21 = 1 и тогда l0 = P(S2)/ P(S1) , (3.8)

Для критерия максимального правдоподобия

П12 = 1/ P(S1) , П21 = 1/ Р(S2), тогда l0 =1. (3.9)

Если приемник использует критерий Неймана-Пирсона, то отношение правдоподобия l(х) становится случайной величиной, так как в равенстве (3.1) Р(у1/S2) = a (задается потребителем). Пороговое отношение правдоподобия определяется как верхний предел интеграла

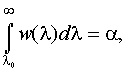(3.10)

где w(l) - плотность распределения отношения правдоподобия l(х).

Правило принятия решения приемником с использованием отношения правдоподобия рассмотрим на следующих примерах.

Условия задачи.

Пусть на вход приемника поступает аддитивная смесь сигнала (дискретная амплитудная модуляция) и помехи:

, где i=1,2;

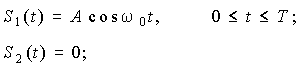
n(t) - флюктуационная помеха типа гауссовского шума с дисперсией .

На протяжении длительности одной элементарной посылки в решающей схеме приемника в синхронные моменты времени t1 и t2 произведено два отсчета(замера) сигнала x(t), причем Dt = t2-t1 больше интервала корреляции помехи n(t). Измеренные значения x(t1)= x1= 0,2 B; x(t2)= x2= 0,3 B. Амплитуда сигнала A=0,4 B.

Определить отношение правдоподобия и принять решение по критерию идеального наблюдателя, какой из двух сигналов (S1 или S2) поступил на вход приемника для двух случаев:

а) ;

б) ; .

Решение задачи(когерентный прием).

1. Найдем отношение правдоподобия .

Плотность вероятности сигнала x(t)=S1(t)+n(t) имеет вид

.

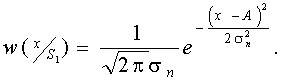Так как на протяжении элементарного сигнала производятся два отсчета, то для нахождения отношения правдоподобия требуется найти двухмерную плотность вероятностей w2(x1x2/s1). Учитывая, что отсчеты некоррелированы (Dt больше интервала корреляции), а помеха распределена по гауссовскому закону, эти отсчеты можно считать независимыми. В этом случае двухмерная плотность вероятностей равна произведению одномерных плотностей

.

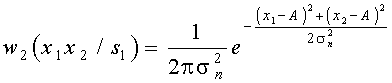Аналогично

.

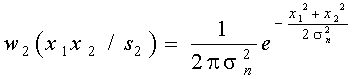Отношение правдоподобия

.

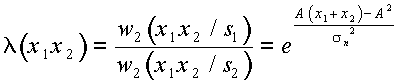Подставляя численные значения A,sn, x1, x2, получим: l (0,2;0,3)= 2,7.

2. Применяем правило решения (3.7 ).

а) Пороговое отношение правдоподобия при P(s1)=P(s2)=0,5

.

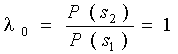В нашем случае l(x1x2)=2,7 > l0=1 и приемник выдает сигнал S1.

б) Пороговое отношение правдоподобия при P(s1)=0,2 и P(s2)=0,8

.

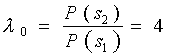В этом случае l(x1x2)=2,7 < l0=4 и приемник выдает сигнал S2.

Полученные результаты вполне объяснимы: в случае a) измеренное значение x(t1)=0,2B соответствует половине амплитуды А=0,4В, а измеренное значение x(t2)=0,3B ближе к сигналу S1, поэтому при равной вероятности сигналов приемник выдает решение в пользу сигнала S1; в случае б) измеренные значения сигнала ближе к S1, но зато сигнал S2(t) встречается в 4 раза чаще, чем сигнал S1(t), и точное решение задачи с учетом всех обстоятельств во втором случае получается в пользу сигнала S2.

Решение задачи (некогерентный прием).

Решим эту же задачу в предположении, что в приемнике используется обычный амплитудный детектор .

Найдем отношение правдоподобия для этого случая. Плотность вероятности x(t) при передаче сигнала S1(t) определяется обобщенным законом Релея

,

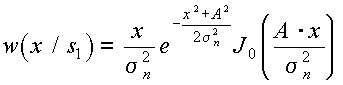а плотность вероятности x(t) при передаче сигнала S2(t) определяется простым законом Релея

.

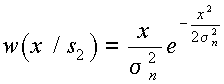Как и в предыдущем примере, отношение правдоподобия будет определяться отношением двухмерных плотностей вероятности. После простых преобразований получаем

.

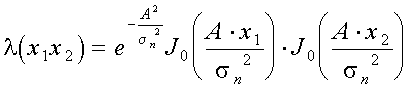Подставляя сюда численные значения А, sn, x1, x2, получим

.

Как и в предыдущем примере, а) l0=1 и б) l0=4.

В обоих случаях l(x1x2)<l0 и в обоих случаях приемник выдает решение в пользу сигнала S2(t).

Сравнивая случаи принятия решения решающей схемой приемника при когерентном и некогерентном приеме, невольно возникает вопрос: почему получаются разные результаты в случае а).

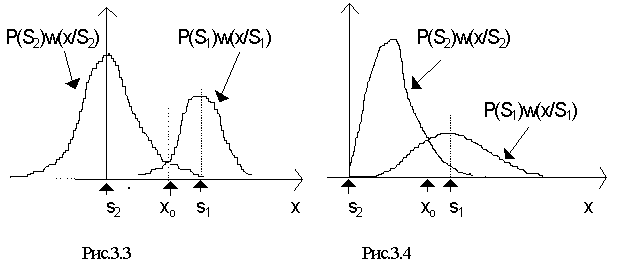
Дело в том, что при когерентном приеме сигналы x(t) распределены по гауссовскому закону и оптимальный порог xo, определяемый точкой пересечения функций P(S1)×w(x/s1) и P(S2)×w(x/s2) (рис. 3.3), в этом случае (когда P(S1) =P(S2) и l0=1) соответствует половине амплитуды сигнала S1(t); измеренные же значения сигнала x(t) близки к пороговому значению и ближе к сигналу S1(t). Однако при некогерентном приеме сигналы x(t) распределены по законам Релея и оптимальный порог xo значительно выше, чем половина амплитуды сигнала S1(t) (рис. 3.4). Поэтому те же измеренные значения x(t1) и x(t2) оказываются дальше от порога в области сигнала S2(t) и решающая схема приемника при заданных в условиях задачи вероятностях сигналов S1(t) и S2(t) выдает решение в пользу сигнала S2(t).

Учитывая, что при когерентном приеме уровень помех на входе решающей схемы существенно ниже, чем при некогерентном, более вероятно, что ошибочное решение принял некогерентный приемник.

4. Оптимальный приемник полностью известных сигналов

Рассмотрим систему связи, в которой передаются два сигнала S1(t) и S2(t) одинаковой длительности Т, произвольной (но известной) формы, априорные вероятности передачи Р(S1) и P(S2); помехи в канале связи флюктуационные, функция плотности распределения которых имеет гауссовский закон распределения вида

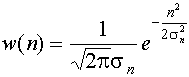, (4.1)

где sn 2 - дисперсия (мощность) помех.

Задан критерий оптимального приема: идеальный наблюдатель (или наблюдатель В.А.Котельникова), который минимизирует среднюю вероятность ошибки

Рош = P(S1)P(y2/S1) + P(S2)P(y1/S2).

Найдем оптимальное правило решения и структурную схему оптимального приемника(оптимального РУ) для указанных выше условий передачи сигналов S1(t) и S2(t).

1. Для решения задачи используем общее для приемников двоичных сигналов правило решения (3.7). В рассматриваемом случае

l0 = P(S2)/P(S1), (4.2)

если l(x)> l0 ,то принимается решение в пользу сигнала S1 ,иначе - S2 .

Для упрощения решения положим вначале, что P(S1)= P(S2) = 0,5; тогда l0=1. В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия.

2. Для определения функций правдоподобия w(x/S1) и w(x/S2) предположим, что на вход приемника поступает сигнал

x(t) = S1(t) + n(t) , например, вида рис. 4.1.

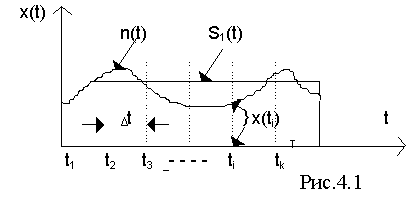
Возьмем n отсчетов сигнала x(t) через одинаковые интервалы Dt, равные интервалу корреляции помехи t0n. Рассмотрим отсчетные значения суммы сигнала S1(t) и помехи n(t) в различных сечениях t i . Так как расстояние между сечениями равно интервалу корреляции помехи, эти сечения некоррелированы между собой. А так как помеха распределена по гауссовскому закону (4.1), то эти сечения также и независимы.

В 1-ом сечении x(t1) = S1(t1) + n(t1);

в 2 -ом сечении x(t2) = S1(t2) + n(t2);

- - - - - - - - - - - - - - - - - - - - - - - - -

в k-ом сечении x(tk) = S1(tk) + n(tk).

Возьмем n отсчетов сигнала x(t) через одинаковые интервалы Dt, равные интервалу корреляции помехи t0n. Рассмотрим отсчетные значения суммы сигнала S1(t) и помехи n(t) в различных сечениях t i . Так как расстояние между сечениями равно интервалу корреляции помехи, эти сечения некоррелированы между собой. А так как помеха распределена по гауссовскому закону (4.1), то эти сечения также и независимы.

Плотность вероятности случайной величины х в k-м сечении при известном сигнале S1(tk) определяется выражением

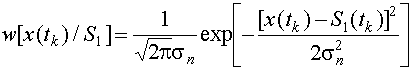, а k-мерная плотность вероятности, благодаря независимости сечений, будет равна произведению одномерных плотностей вероятности различных сечений

.

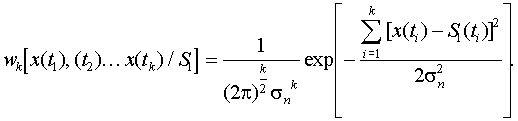Аналогичное выражение можно записать для сигнала S2 , заменив в последнем выражении S1 на S2.

Тогда отношение правдоподобия l(x)= 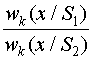и, согласно правилу решения (3.7), если вычисленное значение l(х) > 1 (у нас l0 = 1), то приемник должен выдать сигнал S1 , в противоположном случае - сигнал S2. Отсюда получаем оптимальное правило решения в виде неравенства

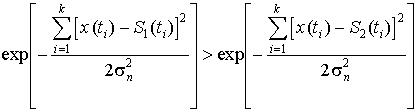, то S1 .

Прологарифмируем это выражение

- [x(t i) - S1(ti)]2 + [x(ti) - S2(ti)]2 >0 , т о S1

или в другом виде

[x(ti) - S1(ti)]2 < [x(ti) - S2(ti)]2 , то S1. (4.3)

Таким образом, оптимальный приемник (идеальный приемник Котельникова) работает следующим образом: определяется среднеквадратическое отклонение поступившего на его вход сигнала x(t) от обоих ожидаемых сигналов ( S1(t) и S2(t) ) и выносится решение в пользу того сигнала, где это среднеквадратическое отклонение меньше.

Если при вычислении условных вероятностей расстояние между сечениями Dt устремить к нулю, т. е. сделать Dt меньше интервала корреляции помехи, работа приемника не улучшится, так как соседние сечения будут сильно коррелированы, но и не ухудшится. Поэтому в правиле решения (4.3) можно заменить суммирование интегрированием.

В интегральной форме получим

[x(ti) - S1(ti)]2 dt < [x(ti) - S2(ti)]2 dt , то S1

или более компактно ( пунктир означает усреднение по времени)

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

[x(ti) - S1(ti)]2 < [x(ti) - S2(ti)]2 , то S1. (4.4)

В соответствии с полученным правилом решения структурная схема приемника будет иметь вид, приведенный на рис. 4.2. Схема содержит два генератора опорных сигналов S1(t) и S2(t), которые генерируют точно такие же сигналы, которые могут поступить на вход приемника, а также два вычитающих устройства, два квадратора, два интегратора и схему сравнения, которая, в соответствии с (4.4), выдает сигналы S1 или S2 .

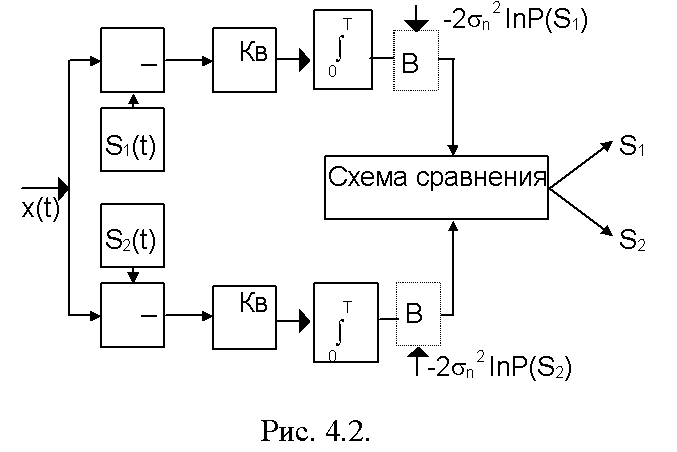
При этом следует подчеркнуть, что приемник Котельникова, как и многие другие приемники дискретных сигналов, выдает на выходе сигналы S1 и S2 , форма которых обычно отличается от формы сигналов в линии связи S1(t) и S2(t). Например, в линии связи эти сигналы могут представлять собой импульсы дискретной частотной модуляции, а на выходе приемника получаем импульсы постоянного тока прямоугольной формы.

Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, т.е. P(S1) не равно P(S2), то неравенство (4.4) принимает несколько другой вид

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

[x(ti) - S1(ti)]2 - 2s2n lnP(S1) < [x(ti) - S2(ti)]2 - 2s2n lnP(S1), то S1, (4.5)

а в структурной схеме рис.4.2 перед схемой сравнения добавляются выравнивающие устройства - В (показаны пунктиром).

Может показаться, что приведенная на рис. 4.2 схема приемника достаточно проста. Однако применяющиеся в схеме местные генераторы S1(t) и S2(t) должны выдавать сигналы по форме идентичные передаваемым сигналам, ожидаемым на входе приемника; поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно.

5. Оптимальный приемник известных сигналов с пассивной паузой

Пусть сигналы S1(t) = A cos w0t и S2(t) = 0 (дискретная амплитудная модуляция - ДАМ).

Подставим S2 = 0 в неравенство (4.4). Получим

_ _ _ _ _ _ _ _ _ _ _ _ _

[x(t) - S1(t)]2 < [x(t) - 0]2 , то S1 .

Преобразуем это выражение

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _

x2(t) - 2x(t)S1(t) + S21(t) < х2(t) , то S1.

_ _ _ _ _ _ _ _ _ _ _

Сокращая на x2(t), получим x(t)S1(t) > S21(t)/2 , то S1 или, окончательно, BxS1(0) > РS1/ 2 , то S1 . (5.1)

Это - оптимальное правило решения приемника для известных сигналов с пассивной паузой. BxS1(0) - функция взаимной корреляции сигнала на входе приемника x(t) и ожидаемого сигнала S1(t), а РS1 - мощность сигнала S1(t) на входе приемника.

В соответствии с правилом (5.1) структурная схема приемника примет вид (рис. 5.1). В отличие от схемы (рис. 4.1) здесь вместо вычитания производится перемножение входного сигнала x(t) на опорное напряжение местного генератора сигналов S1(t) (в данном случае S1(t) = A cos w0t). Приведенная схема называется корреляционным приемником, так как вычисляется функция взаимной корреляции входного сигнала x(t) и местного сигнала S1(t), а в схеме сравнения функция корреляции сравнивается с некоторым порогом x0, значение которого равно 0,5РS1 ( когда P(S1) не равно P(S2), то в соответствии с неравенством (4.5) значение порога становится равным 0,5РS1 +s2n lnl0 ).

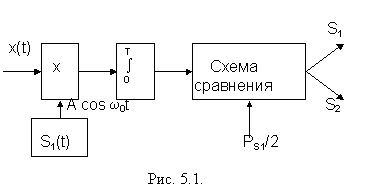
Правило решения (5.1) имеет простой физический смысл. Если функция взаимной корреляции сигнала x(t) и сигнала S1(t) достаточно велика, значит x(t) кроме помехи содержит также сигнал S1(t) и приемник выдает сигнал S1(t). Если же эта функция взаимной корреляции достаточно мала, значит x(t) не содержит сигнала S1(t), т.е. x(t) содержит только одну помеху. В этом случае приемник выдает сигнал S2(t).

Недостатком рассмотренной схемы является то, что для ее работы требуется знание мощности сигнала S1(t) на входе приемника. Однако очень часто эта мощность не является постоянной из-за замираний, изменения остаточного затухания в линиях связи и пр. Устройство для измерения мощности сигнала S1(t) на входе приемника становится сложным и недостаточно точным, что затрудняет практическую реализацию оптимального правила решения.

6. Оптимальный приемник известных сигналов с активной паузой

Пусть S1(t) = A cos w1t, S2(t) = A cos w2t, 0 £ t £ T (дискретная частотная модуляция - ДЧМ).

Преобразуем выражение (4.4)

x2(t) - 2x(t)S1(t) + S21(t) < х2(t) - 2x(t)S2(t) + S22(t) , то S1.

Здесь S21(t) = S22(t), так как это мощности сигналов S1(t) и S2(t), а эти мощности равны между собой из-за равенства амплитуд этих сигналов. После очевидных сокращений получаем следующее оптимальное правило решения x(t)S1(t) > x(t)S2(t) , то S1 или, более кратко BxS1(0) > BxS2(0), то S1 . (6.1)

Смысл полученного выражения очевиден: если функция взаимной корреляции входного сигнала x(t) и сигнала S1(t) больше, чем функция взаимной корреляции сигналов x(t) и S2(t), то x(t) содержит, кроме помехи, сигнал S1(t).

Cигналы S1(t) и S2(t), используемые для вычисления функций взаимной корреляции, должны генерироваться в схеме приемника и совпадать по частоте и фазе с оптимальными сигналами, которые поступают или могут поступать на вход приемника.

Схема, реализующая правило решения (6.1), также называется корреляционным приемником и приведена на рис. 6.1.

Схема содержит два коррелятора по числу передаваемых сигналов При приеме сигналов ДЧМ местные генераторы генерируют сигналы A cos w1t и A cos w2t. Эта же схема пригодна для приема дискретной фазовой мо-дуляции (ДФМ), если в качестве опорных сигналов использовать сигналы S1(t) = A cos w0t и S2(t) = - A cos w0t.

Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, т.е. P(S1) не равно P(S2), то неравенство (6.1) принимает несколько другой вид

x(t)S1(t) - s2n lnP(S1) > x(t)S2(t) - s2n lnP(S2) , то S1 , (6.2)

а в структурной схеме рис.6.1 перед схемой сравнения добавляются выравнивающие устройства, аналогично показанным на рис.4.2 .

Однако для приема сигналов ДФМ схему рис. 6.1. можно упростить, если использовать один общий коррелятор (рис. 6.2).

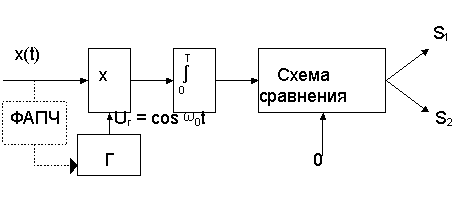
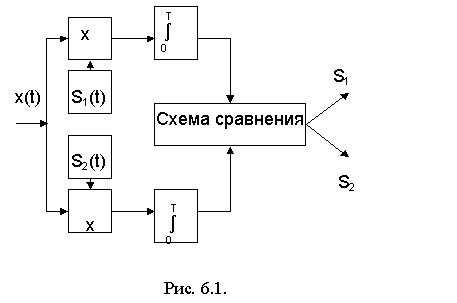
Если x(t) содержит сигнал S1(t) = A cos w0t, на выходе интегратора имеем напряжение, равное BxUг (0) > 0 . Если же x(t) содержит сигнал S2(t) = - A cos w0t, то на выходе интегратора имеем напряжение, равное BxUг (0) < 0. Напряжение на выходе интегратора сравнивается с пороговым напряжением, равным нулю, и в зависимости от результатов сравнения выдает сигналы S1 или S2.

В рассмотренных здесь корреляционных приемниках осуществляется когерентный прием сигналов, поэтому применяемые в приемниках генераторы должны выдавать опорные сигналы S1(t) и S2(t), совпадающие с аналогичными принимаемыми сигналами с точностью до фазы. Поэтому для работы рассмотренных здесь корреляционных приемников требуется синхронизация местных генераторов сигналов. На рис. 6.2, например, пунктиром показана цепь синхронизации опорного генератора Г входным сигналом x(t) с помощью специального устройства фазовой автоподстройки частоты (ФАПЧ).

7. Вероятность ошибки в оптимальном приемнике

Средняя вероятность ошибки в соответствии с формулой (2.4) зависит от вероятности неправильного приема сигналов S1 и S2 . Однако при применении идеального приемника Котельникова канал связи предполагается симметричным, т.е. P(y2/S1) = P(y1/S2). Поэтому формула (2.4) упрощается. В нашем случае Pош = P(y2/S1). Эту формулу мы возьмем за основу при определении вероятности ошибки в приемнике Котельникова.

Допустим, нам известно, что на вход приемника поступает сигнал S1(t). В этом случае, в соответствии с правилом решения приемника Котельникова (4.4), должно выполняться следующее неравенство

[x(t) - S1(t)]2 < [x(t) - S2(t)]2 . (7.1)

Однако, несмотря на поступление сигнала S1(t), при сильной помехе знак неравенства может измениться на противоположный, в результате чего приемник вместо сигнала S1(t) выдает сигнал S2(t), то есть произойдет ошибка. Вероятность искажения сигнала S1(t) можно определить как вероятность изменения знака неравенства (7.1), если подставить туда x(t) = S1(t) + n(t).

После очевидных преобразований получаем

Pош = P(y2/S1) = P{n2(t) > [n(t) + S1(t) - S2(t)]2} =P{0 > 2 n(t) [S1(t) - S2(t)] + [S1(t) - S2(t)]2} =

= P{1/T 2n(t) [S1(t) - S2(t)]dt + 1/T [S1(t) - S2(t)]2dt < 0}.

Сокращая на Т, получаем

Pош = P{ n(t) [S1(t) - S2(t)]dt + 0,5 [S1(t) - S2(t)]2dt < 0}.

Обозначим в этом выражении:

n(t) [S1(t) - S2(t)]dt = m , [S1(t) - S2(t)]2dt = Еэ (7.2)

С учетом этих обозначений вероятность искажения сигнала S1 будет определятся формулой

Pош = P{m < 1/2× Eэ}. (7.3)

В этой формуле Eэ - энергия разности сигналов S1(t) - S2(t), называемая "эквивалентной энергией" , а m - некоторая случайная величина, зависящая от помехи n(t) и разности сигналов S1(t) - S2(t).

Так как помеха n(t) имеет гауссовское распределение, а величина m есть результат линейной операции над n(t) , то и величина m распределена также по гауссовскому закону

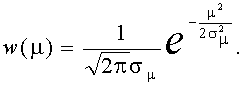
Тогда, в соответствии с (7.3)

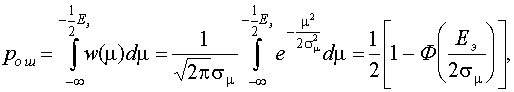(7.4)

где 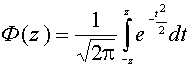- табулированный интеграл вероятностей.

Можно доказать,что при флюктуационной помехе на входе приемника со спектральной плотностью помехи N0 дисперсия величины m определяется формулой s2m = N0Eэ /2.

Подставляя это значение s2m в (7.4) получим окончательно 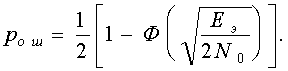(7.5)

Таким образом, в приемнике Котельникова вероятность ошибки полностью определяется эквивалентной энергией сигналов и спектральной плотностью помехи и от полосы пропускания приемника не зависит. На практике обычно на входе приемника все-таки ставят полосовой фильтр, так как в канале связи, кроме флюктуационных помех, часто встречаются также другие помехи (от соседних каналов, импульсные и др.)

Формула (7.5) является достаточно общей. Для конкретных видов модуляции в канале связи эту формулу видоизменяют, для чего вычисляют соответствующее значение Eэ . При этом для различных видов модуляции Eэ определяют через энергию одного из сигналов, а в окончательную формулу вводят величину

h20 = E1/N0 . (7.6)

Следовательно, в приемнике Котельникова, который также называется когерентным (в приемнике известна фаза принимаемого сигнала) вероятность ошибки зависит не от отношения мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличить его энергию за счет увеличения его длительности, что дает дополнительные возможности в построении помехоустойчивых систем связи.

8. Потенциальная помехоустойчивость различных видов дискретной модуляции

1. Дискретная амплитудная модуляция.

S1(t) = A cos w0t , S2(t) = 0 , 0 < t < T;

Eэ = S21(t)dt = E1 (Eэ равна энергии первого сигнала);

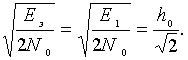
Подставив эту величину в формулу (7.6), получим

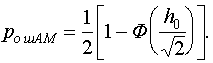(8.1)

2. Дискретная частотная модуляция.

S1(t) = A cos w1t ; S2(t) = A cos w2t , 0 < t < T.

Eэ = [S1(t) - S2(t)]2dt = S21(t)dt + 2 S1(t)S2(t)dt + S22(t)dt= E1 + 2TBS1S2(0) + E2.

При частотной модуляции сигналы S1(t) и S2(t) являются взаимоортогональными, поэтому их функция взаимной корреляции равна нулю. Кроме того, благодаря равной амплитуде сигналов S1(t) и S2(t) E1=E2. В результате Eэ = 2E1 , а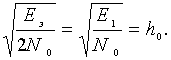

Подставив эту величину в формулу (7.6), получим

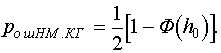(8.2)

3. Дискретная фазовая модуляция.

S1(t) = A cos w0t, S2(t) = - A cos w0t = - S1(t) , 0 < t < T;

[ Eэ =2S1(t)]2dt = 4E1,

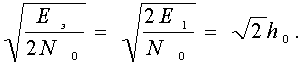
Подставив эту величину в формулу (7.6), получим

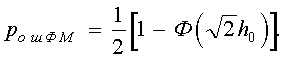(8.3)

Сравнивая между собой формулы (8.1), (8.2), (8.3), видим, что для достижения заданной вероятности ошибки при ДЧМ требуется величина h0 в больше, чем при ДФМ, а при ДАМ - в 2 раза больше, чем при ФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ - четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.

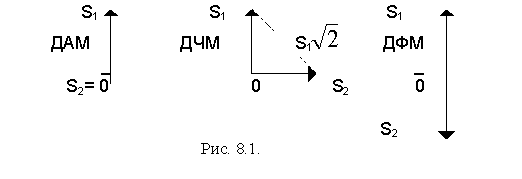
Из рис. 8.1 видно, что при ДАМ расстояние между векторами сигналов S1 и S2 равно длине вектора S1, при ДЧМ (взаимоортогональные сигналы) это расстояние равно S1 , при ДФМ (противоположные сигналы) это расстояние равно 2S1. Энергия же пропорциональна квадрату разности сигналов.

Следует заметить, что приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ и ДФМ относились к максимальным (пиковым) мощностям этих сигналов. В этом смысле, например, при переходе от ДЧМ к ДАМ мы имеем двухкратный выигрыш в пиковой мощности.

Однако, сигналы ДАМ имеют пассивную паузу (мощность сигнала в паузе равна нулю), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двухкратный выигрыш. С учетом этого обстоятельства, при переходе от ДЧМ к ДАМ двухкратный проигрыш по пиковой мощности компенсируется двухкратным выигрышем за счет пассивной паузы сигналов ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными. Однако следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная.

Отметим еще раз, что приемник Котельникова обеспечивает наибольшую предельно-допустимую (потенциальную) помехоустойчивость. Это достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а также длительность сигнала Т, так как интегрирование (фильтрация) осуществляется в течение этого времени. Решение о принятом сигнале обычно осуществляется в конце каждого интервала Т, для чего в приемнике должна иметься специальная система синхронизации элементов сигнала.

9. Оптимальная фильтрация дискретных сигналов

Оптимальный приемник (рис.9.1) является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого сигнала x(t) и ожидаемого Si(t), благодаря чему обеспечивается максимально - возможное отношение сигнал/шум h20.

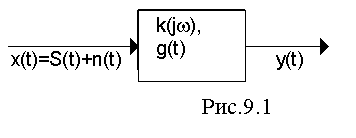
Поскольку операция определения функции корреляции является линейной, ее можно реализовать в некотором линейном фильтре, характеристики которого (комплексная передаточная характеристика K(jw) и импульсная характеристика g(t) являются такими, что отношение сигнал/шум на его выходе получается максимальным, причем h2max = h20.

Найдем характеристики фильтра, когда помеха n(t) является флюктуационной со спектральной плотностью Gn(w) = N0,, w ³ 0.

Пусть сигнал на входе фильтра имеет комплексный спектр S(jw). Тогда сигнал на выходе фильтра y(t) можно определить с помощью преобразования Фурье

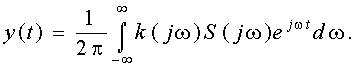
Нас интересуют значение y(t) в момент принятия решения (момент отсчета t0), поэтому, заменив t на t0, получим

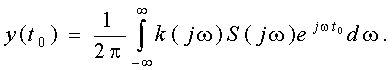(9.1)

Чтобы получить максимальную величину y(t0), нужно найти оптимальную характеристику фильтра k(jw). Для этой цели можно воспользоваться известным неравенством Шварца-Буняковского, имеющим вид

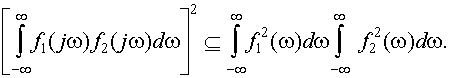
Легко проверить, что данное неравенство превращается в равенство при условии,что

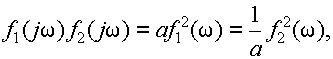
где a - любая произвольная постоянная. В нашем случае, применительно к формуле (9.1), величина y(t0) будет максимальной при условии

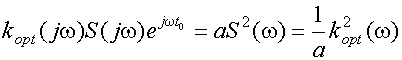(9.2)

(это уже есть условие оптимальности характеристики K(jw), поэтому здесь и в дальнейшем K(jw) заменено на Kopt(jw) ).

Подставляя в левую часть формулы (9.2)

(9.3)

(9.4)

получаем

или, сокращая на S(w), будем иметь

. (9.5)

Последнюю формулу можно представить в виде двух составляющих, позволяющих найти амплитудно-частотную характеристику оптимального фильтра Kopt(w) и фазо-частотную характеристику jk(w):

; (9.6)

(9.7)

откуда (9.8)

Здесь js(w) - фазо-частотный спектр входного сигнала; wt0 - "запаздывающий" множитель, учитывающий то, что "отсчет" величины сигнала на выходе фильтра производится в момент t0 , когда возникает максимум выходного сигнала фильтра.

Условие (9.6) имеет простой физический смысл: фильтр должен лучше пропускать составляющие спектра сигнала, имеющие большую амплитуду и в меньшей степени пропускать составляющие сигнала, имеющие меньшую амплитуду.

Условие (9.7) имеет также простой физический смысл: в момент отсчета (t0) все частотные составляющие спектра выходного сигнала имеют нулевую фазу, благодаря чему выходное напряжение в момент t0 имеет наибольшее отношение мощности сигнала к мощности помехи .

Условия (9.6) и (9.8) можно объединить в одно, представив передаточную характеристику в комплексной форме

(9.9)

Можно, наконец, последнюю формулу представить в следующем виде

(9.10)

Здесь S*(jw) - комплексно-сопряженный спектр по отношению к S(jw).

Отношение сигнал/помеха определяется , как обычно, формулой

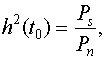(9.11)

где - мощность сигнала на выходе фильтра в момент t0 ;

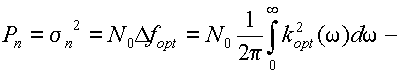(9.12)

мощность (дисперсия) помехи на выходе фильтра,

Dfopt - эффективная полоса пропускания оптимального фильтра.

Подставляя в (9.11) выражения (9.1) и (9.12) с учетом (9.2), получим

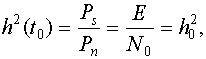(9.13)

где 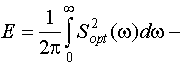энергия сигнала S(t) на входе фильтра.

Из (9.13) видно, что отношение h2(t0) численно равно отношению энергии сигнала к спектральной плотности помехи (как в приемнике Котельникова) и не зависит от формы сигнала. А так как энергия сигнала равна произведению мощности сигнала на его длительность, то для повышения помехоустойчивости систем связи с использованием согласованных фильтров можно увеличивать длительность элементарных сигналов, что и делается в широкополосных системах связи.

При применении в демодуляторе приемника согласованных фильтров в сочетании с когерентным способом приема можно добиться потенциальной помехоустойчивости.

Импульсная характеристика оптимального фильтра (отклик фильтра на дельта-функцию) определяется известным выражением

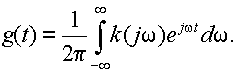
Подставив сюда значение Kopt(jw) из (9.10), получим

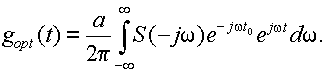
Интегрирование в последней формуле производится по всем частотам от -¥ до +¥; поэтому знак перед w в этой формуле можно заменить на противоположный, что не приведет к изменению результата вычисления интеграла. В результате получим

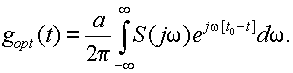(9.14)

А так как, на основании преобразования Фурье

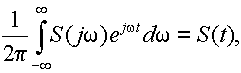(9.15)

то, сравнивая (9.14) и (9.15), получаем

(9.16).

Таким образом, функция g(t) отличается от сигнала S(t) только постоянным множителем а , смещением на величину t0 и знаком аргумента t (то есть функция g(t) является зеркальным отображением сигнала S(t) , сдвинутым на величину t0.

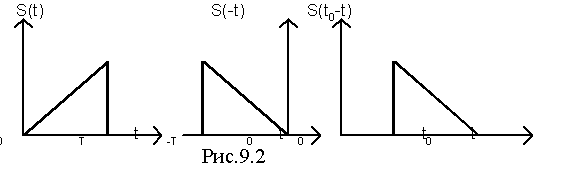
На рис. 9.2 в качестве примера приведен некоторый сигнал S(t), зеркально перевернутый сигнал S(- t) и функция g(t) = aS(t0 - t).

Как уже говорилось, величину t0 обычно берут равной длительности сигнала Т. Если взять t0 < T, то получается физически неосуществимая система (отклик начинается раньше поступления входного воздействия).

Сигнал y(t) на выходе линейной системы при поступлении на ее вход сигнала x(t) определяется известным интегралом Дюамеля

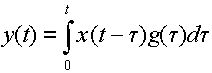. (9.17)

Пусть на вход оптимального фильтра поступает аддитивная смесь, содержащая сигнал S(t) , с которым фильтр согласован, и помеха n(t) ( это может быть флюктуационная помеха или какой-нибудь детерминированный сигнал, с которым фильтр не согласован) x(t)=S(t)+n(t) ,

Подставляя x(t) и (9.16) в (9.17), получим

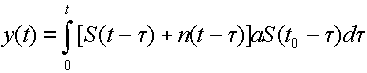, (9.18)

заменяя t­0 на Т, получим

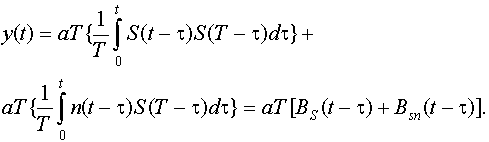(9.19)

Таким образом, на выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, а под действием помехи функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха(без сигнала), на выходе получаем только функцию взаимной корреляции помехи и сигнала, с которым фильтр согласован.

В формуле (9.19) а - любой произвольный множитель, поэтому произведение а Т можно заменить на произвольный множитель b. В момент времени t=T (момент отсчета) формула (9.19) дает

(9.20)

Примечание. Если на вход согласованного фильтра поступает флюктуационная помеха, то теоретически функция взаимной корреляции Bsn(0) должна быть равна нулю, так как сигнал и помеха являются независимыми функциями времени. Однако на практике Bsn¹ 0 , так как при вычислении функции взаимной корреляции требуется бесконечно большое время интегрирования. В нашем же случае интегрирование ведется за время, равное Т. Поэтому формулы (9.19) и (9.20) являются приближенными.

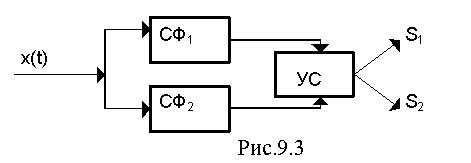
Результаты фильтрации не зависят от формы сигнала. Следовательно фильтр может быть применен и без детектора. Тогда оптимальный приемник полностью известных сигналов (рис. 6.1) может быть реализован в виде двух согласованных фильтров - СФ 1 , СФ 2 и устройства сравнения - УС (рис.9.3).

Примеры согласованных фильтров.

Рассмотрим согласованный фильтр для прямоугольного импульса длительности Т (рис 9.4 а).

Спектральная плотность такого импульса равна

.

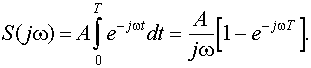Для согласованного фильтра, в соответствии с (9.10) для случая t0 = T

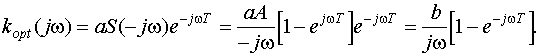(9.21)

Пользуясь последним выражением, можно легко построить схему фильтра для данного случая. Так из теории электрических цепей известно, что деление на jw означает интегрирование сигнала, а множитель е-jwT означает задержку сигнала на время Т. В результате схема фильтра будет содержать интегратор, линию задержки и вычитатель (рис. 9.4).

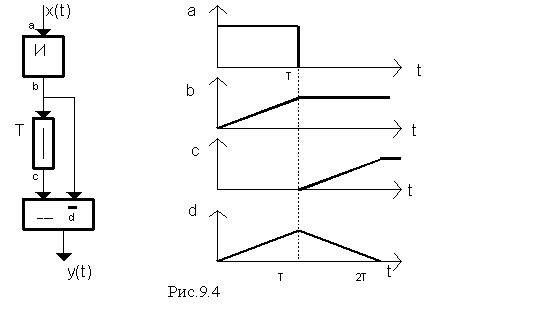
Таким образом, на выходе фильтра получился треугольный импульс с основанием 2Т (это - функция корреляции входного импульса прямоугольной формы). То, что выходной импульс имеет в два раза большую длительность, чем входной, является недостатком оптимального фильтра, так как "хвост" выходного сигнала на отрезке времени от Т до 2Т будет накладываться на выходной сигнал следующего импульса. Поэтому на практике часто применяют упрощенную схему фильтра, содержащую интегриру ющую RC -цепь (RC>> T) и ключ К (рис. 9.5).

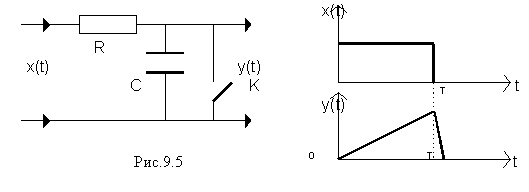
В момент T окончания входного импульса ключ К замыкается, конденсатор интегратора быстро разряжается через ключ и схема оказывается готовой к приему следующего импульса.

Оптимальный фильтр для приема радиоимпульсов с прямоугольной огибающей может быть построен аналогичным образом, однако RC - цепочка должна быть заменена колебательным контуром с достаточно высокой добротностью. Фильтры с ключами называются "кинематическими" фильтрами.

10. Прием дискретных сигналов с неизвестной фазой

В приемнике Котельникова местные генераторы опорных сигналов S1(t) и S2(t) должны генерировать сигналы с точностью до фазы принимаемых сигналов. Для этого фаза принимаемого сигнала Si (t) измеряется и используется для синхронизации опорных генераторов. Такой приемник называется приемником с известной фазой (когерентным приемником) в отличие от приемника с неизвестной фазой ( некогерентного приемника).

Прием сигналов с неизвестной фазой возможен в следующих случаях:

1. формирование сигналов Si(t) в передатчике производится без учета фазы несущего колебания, в результате чего фаза несущего колебания в каждом сигнале Si (t) является случайной;

2. в канале связи наблюдаются случайные скачки фазы с большой дисперсией;

3. реализация когерентного приемника экономически нецелесообразна из-за необходимости использования синхронизируемых опорных генераторов сигналов Si(t).

Посмотрим, что произойдет при наличии случайного сдвига фаз.

Пусть сигнал S1(t) = A cos w0t, а опорный сигнал приемника Uоп (t) = A cos (w0t + j).

После перемножения и интегрирования этих сигналов получаем

S1(t)×Uоп1(t) = A2cosw0t×cos(w0t + j)dt = A2 [0,5cosj + 0,5cos(2w0t + j)]dt = 0,5A2cosj.

Отсюда видно, что при наличии сдвига j функция взаимной корреляции умножается на cosj<0. Только при j=0 cosj=1 и приемник будет оптимальным и когерентным. При наличии сдвига фаз помехоустойчивость приемника уменьшается.

Рассмотрим в качестве примера оптимальный некогерентный приемник двух сигналов ДЧМ (рис. 10.1).

На входе приемника разделение сигналов двух частот (w1 и w2) осуществляется с помощью квадратурной схемы приема и двух ветвей обработки сигналов S1(t) и S2(t). Для этого каждая ветвь имеет два перемножителя, генератор опорного напряжения частоты (w1 или w2), фазовращатель на 900. Далее с помощью интеграторов, квадраторов (Кв) и сумматора определяется значение амплитуды сигнала U2i = U2u1 + U2u2 .

С выходов аналоговых сумматоров сигналы подаются на схему сравнения, которая реализует правило решения:

если U21 > U22 , то сигнал S1; иначе сигнал S2. (10.1)

Если интеграторы в схеме рис. 10.1 являются оптимальными, то для сигналов с неизвестной фазой (и одинаковой энергией каждого сигнала) реализуется оптимальное правило решения вида

Фопт(х) = max Ui (10.2)

Приведенная схема нечувствительна (инвариантна) по отношению к фазам приходящих сигналов (или фазам опорных генераторов Г1 и Г2). Чтобы в этом убедиться, рассмотрим работу верхней половины схемы, когда на ее вход поступает сигнал S1(t) = A cos(w0t + j1), где j1 - случайная (неизвестная) фаза сигнала. Помехи на входе приемника учитывать не будем.

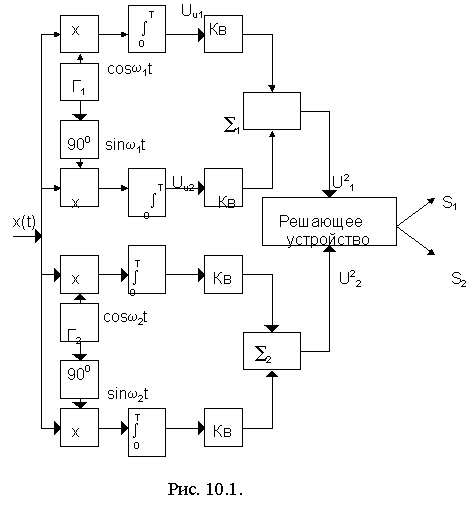
Найдем величину U1 на выходе первого сумматора, если два опорных напряжения изменяются по закону cosw1t и sinw1t (cдвинуты на 900, т.е. находятся в квадратуре). Вычислим сначала напряжения на выходе первого и второго интеграторов.

Uu1 = Acosw1t×cos(w1t + j1)dt = 0,5A cosj1dt + 0,5A cos(2w1t + j1)]dt = 0,5×A×T×cosj1. (10.3)

Аналогично получим Uu2 = 0,5×A×T×sinj1.

Отсюда

U21 = U2u1 + U2u2 = 0,25×A2T2(cos2j1 + sin2j1) = 0,25×A2T2. . (10.4)

Таким образом, на выходе первого сумматора получим сумму квадратов напряжений Uu1 и Uu2 , пропорциональную энергии сигнала S1. От фазы сигнала эта величина не зависит. В этом и заключается преимущество подобного способа приема.

Следует заметить, что на первом входе решающей схемы при поступлении на вход приемника сигнала S1(t), кроме найденной величины Uu1, будет поступать также помеха n1(t), прошедшая вместе с сигналом весь тракт обработки сигнала S1 . На втором входе решающего устройства будет существовать помеха n2(t).

При наличии помехи на входе приемника при обработке сигнала и помехи происходит сложное их взаимодействие. Подробно рассматривать этот вопрос мы не будем. Заметим только, что в процессе анализа помеха n(t) разлагается на квадратурные составляющие, синфазные с опорными напряжениями coswt и sinwt.

Оптимальное правило решения (10.2) для двух сигналов ДЧМ может быть реализовано и с помощью схемы рис.10.2.

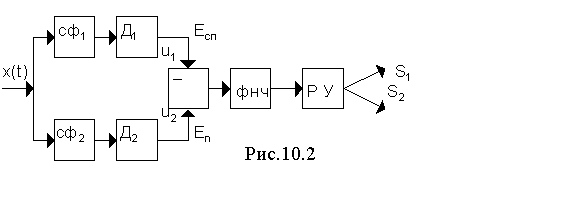
На входе приемника сигнал x(t) представляет собой сумму S1(t) = A cos w1t или S2(t) = A cos w2t и помехи n(t).

В схеме приемника имеются оптимальные фильтры СФ1 и СФ2 , согласованные с сигналами S1(t) и S2(t). Далее идут амплитудные детекторы D1 и D2 , схема вычитания, фильтр нижних частот и решающее устройство РУ (схема сравнения), которое, в зависимости от полярности сигнала на его входе, выдает сигналы S1 или S2.

Пусть на вход приемника поступает сигнал S1(t). Тогда на выходе первого фильтра мы будем иметь сумму сигнала S1(t) и помехи n1(t), а на выходе второго фильтра - только помеху n2(t) . Реализации помех n1(t) и n2(t) - различные, так как каждая помеха прошла через свой полосовой фильтр. После детектирования сигналов на выходе детектора D1 мы будем иметь огибающую суммы сигнала и помехи U1 = Eсп, распределенную по обобщенному закону Релея

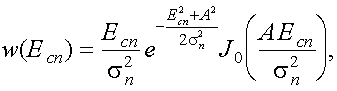(10.5)

а на выходе детектора D2 получим огибающую помехи U2 = Eп , распределенную по простому закону Релея

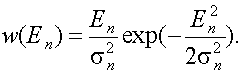(10.6)

При малой помехе напряжение на выходе первого детектора Eсп будет больше, чем напряжение на выходе второго детектора Eп , разность Eсп - Eп будет положительной и решающее устройство выдаст сигнал S1 . Однако, при сильной помехе может случиться, что Eп превысит Eсп и схема ошибочно выдаст сигнал S2. Сказанное поясняется рисунком 10.3, на котором приведены зависимости Eсп(t) и Eп(t) . Как видно из рисунка, на интервале времени Dt Eп(t) > Eсп(t); вероятность этого события и есть вероятность ошибки на выходе данного приемника.

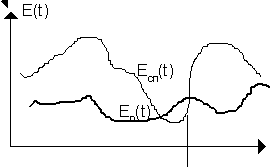
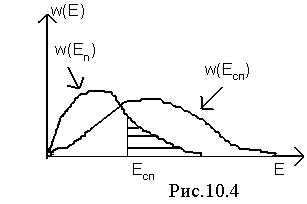
На рис. 10.4 приведены графики плотностей вероятности простого и обобщенного законов Релея в соответствии с формулами (10.6) и (10.7). Допустим, в какой-то момент времени величина Eсп на выходе первого детектора известна. Тогда можно определить вероятность ошибки как вероятность того, что огибающая помехи Eп превысит данное значение Eсп (заштрихованная часть рисунка)

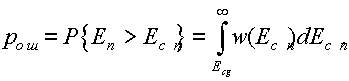(10.7)

Подставляя сюда w(Eп) по формуле (10.7) и производя интегрирование, получаем 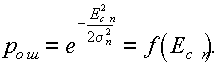(10.8)

В результате мы получили зависимость вероятности ошибки как функцию Eсп. Величина Eсп на рис. 10.4 известна. Однако в действительности Eсп - случайная величина, определяемая распределением (10.5). Поэтому величину Pош = f(Eсп) надо усреднить по всем возможным изменениям Eсп (от 0 до ¥).

Тогда

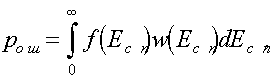(10.9)

Если сюда подставить формулы (10.5) и (10.8), то после интегрирования получим

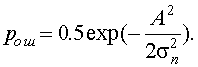
Но А2/2 есть мощность сигнала S1(t).

Введем обозначение 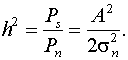(10.10)

Тогда окончательно получим

pошЧМ нкг (10.11)

Помехоустойчивость некогерентного приема ниже, чем помехоустойчивость оптимального приемника Котельникова.

Если фильтры на входе приемника являются оптимальными, то

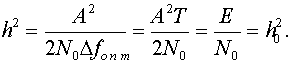(10.12)

Можно показать, что при дискретной амплитудной модуляции вероятность ошибки при некогерентном приеме определяется формулой

(10.13)

Отсюда видно, что при переходе от ДАМ к ДЧМ имеется энергетический выигрыш (по максимальной мощности), равный двум. С точки зрения средних мощностей, как уже говорилось, ДАМ и ДЧМ эквивалентны.

При сравнении помехоустойчивости когерентного и некогерентного приемов можно убедиться, что при когерентном приеме вероятность ошибки значительно меньше, чем при некогерентном приеме. Это объясняется тем, что при некогерентном приеме флюктуационная помеха полностью влияет на помехоустойчивость приема. При когерентном приеме на вероятность ошибки влияет только синфазная составляющая помехи, квадратурная же составляющая подавляется синхронным детектором. В результате этого когерентный прием обеспечивает практически двухкратный энергетический выигрыш по сравнению с некогерентным приемом, так как мощность огибающей помехи в два раза выше мощности ее квадратурных составляющих.

11. Прием сигналов ОФМ

Дискретная фазовая модуляция обеспечивает наиболее высокую помехоустойчивость приема дискретных сигналов. Однако при практической реализации схемы приемника возникают трудности с получением опорного напряжения. Как видно из рис. 6.2, для получения опорного напряжения используется генератор, синхронизируемый входным сигналом. Под действием случайных помех фаза опорного генератора может скачком измениться на 180о, тогда опорное напряжение будет совпадать по фазе не с сигналом S1(t), а с сигналом S2(t). А так как при ДФМ S2(t)= -S1(t), то неправильная фаза опорного генератора приводит к появлению "обратной работы", когда сигналы S1(t) принимаются как S2(t) и наоборот ( для двоичного сигнала это означает, что сигналы "1" превращаются в "0", а "0" превращаются в "1").

Для устранения опасности "обратной работы" широко применяется "относительная" фазовая модуляция (ОФМ). Если при обычной дискретной фазовой модуляции прием осуществляется путем сравнения фазы приходящего сигнала с фазой опорного генератора, то при ОФМ осуществляется сравнение фазы каждой посылки с фазой предыдущей посылки. Если фаза очередной посылки совпадает с фазой предыдущей, то приемник выдает "1", если же фазы противоположны, приемник выдает "0".

Возможен когерентный и некогерентный прием сигналов ОФМ. При когерентном приеме в приемнике используется опорный генератор, а снятие (устранение) относительности осуществляется после детектирования сигналов (рис. 11.1). Для этой цели сигнал с выхода синхронного детектора подается на ячейку памяти ЯП и схему сравнения полярностей ССП. На другой вход схемы ССП подается сигнал с ячейки памяти, задержанный на время, равное длительности элементарной посылки принимаемых сигналов.

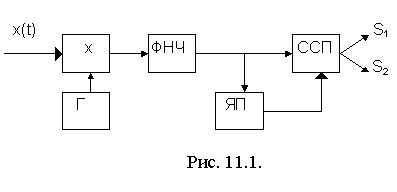
Таким образом, схема сравнения полярностей сравнивает полярности принимаемой посылки и предыдущей посылки. При совпадении полярностей схема выдает "1", при несовпадении - "0".

Особенностью ОФМ является сдваивание ошибок, возникающих из-за помех, так как любая искаженная посылка поступает на схему сравнения полярностей дважды: сначала непосредственно, а затем - через ячейку памяти. При малой вероятности ошибок эта вероятность вдвое больше, чем вероятность ошибки при приеме сигналов дискретной фазовой модуляции

или

(11.1)

Схема приемника ОФМ для некогерентного приема приведена на рис. 11.2. В этой схеме вместо опорного генератора используется линия задержки, задерживающая входной высокочастотный сигнал на время, равное длительности элементарной посылки. В отличие от предыдущей схемы, опорное напряжение в схеме рис. 11.2 содержит, кроме высокочастотного напряжения предыдущей посылки, также составляющую помехи, в результате чего эта схема обеспечивает меньшую помехоустойчивость, чем схема когерентного приема.

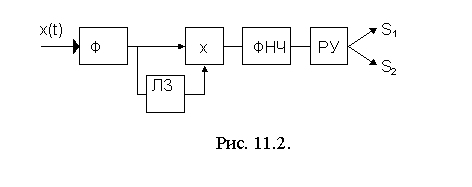
Вероятность ошибки при этом определяется формулой

(11.2)

Иногда для некогерентного приема ОФМ применяют квадратурную схему приема (для сигналов ДЧМ такая схема была приведена на рис. 10.1).

Максимальная помехоустойчивость приемников рис. 10.1 и 10.2 при флюктуационных помехах имеет место в том случае, когда в качестве фильтров ФНЧ используются оптимальные фильтры. При этом обеспечивается и минимум вероятности ошибки, вычисляемой по формулам (11.1, 11.2).

12. Прием дискретных сигналов со случайной амплитудой

В некоторых системах связи амплитуда принимаемого сигнала является случайной из-за мультипликативных помех. В этом случае, для нахождения вероятности ошибки в зависимости от способа приема сигналов, вначале определяют по известным формулам вероятность ошибки pош(h), как для канала с постоянными параметрами.

Например, для ЧМ КГ

для ЧМ НКГ

и так далее.

Затем определяется закон распределения w(h), учитывающий случайные изменения амплитуды сигнала. Наконец,, находится среднее значение Pош как математическое ожидание pош(h) по формуле

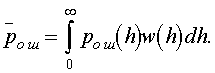(12.1)

Вычислим вероятность ошибки в канале с релеевскими замираниями.

Пусть S(t) = A coswt., мощность помехи s2п . В случае релеевских замираний амплитуда сигнала А является случайной и ее плотность вероятности равна

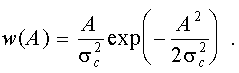(12.2)

Здесь s2с - дисперсия замираний, характеризующая разброс амплитуд сигнала в процессе замираний.

Найдем w(h).

По определению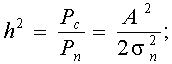

откуда (12.3)

Здесь мы имеем дело с функциональной зависимостью h от А. В соответствии с известным правилом определения функций распределения функционально-связанных случайных величин можно записать

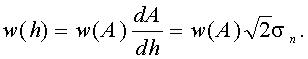
Подставив сюда w(A) из (12. 2) и заменив потом А на h по формуле (12.3), получим

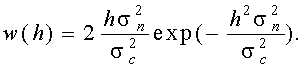(12.4)

Введем понятие среднего значения отношения сигнал / шум

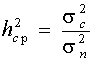(12.5)

и подставим это выражение в (12.4); тогда

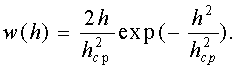(12.6)

Отсюда видно, что величина h подчиняется, как и величина А, релеевскому закону распределения. Этого и следовало ожидать, так как h и А связаны линейной зависимостью (12.3).

Подставив теперь (12.6) в (12.1), получим общее выражение для вероятности ошибки в канале с релеевскими замираниями

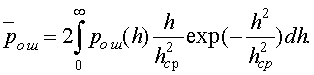(12.7)

Рассмотрим несколько частных случаев.

1. Для приема сигналов ДЧМ некогерентным приемником получим

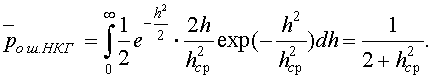(12.8)

2. Для случая приема сигналов ДЧМ когерентным приемником получим

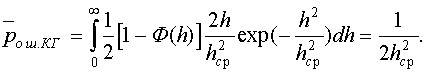(12.9)

Сравнивая формулы (12.8) и (12.9), видим, что, как и в каналах с постоянными параметрами, в каналах с замираниями переход от некогерентного к когерентному приему дает энергетический выигрыш, примерно равный двум. Если сравнить помехоустойчивость систем связи с каналами без замираний и системы с замираниями, то можно сделать вывод, что в каналах с замираниями для достижения малой вероятности ошибок мощность сигнала должна быть увеличина по сравнению с каналами без замираний в сотни раз. Поэтому в каналах с замираниями для уменьшения вероятности ошибок используются другие методы повышения помехоустойчивости (например, разнесенный прием). Кроме того, ошибки в таких каналах часто "пакетируются", то есть встречаются интервалы времени, внутри которых вероятность ошибок резко увеличивается.

14. Мера количества информации в дискретном сообщении

Система связи служит для передачи сообщений от отправителя к получателю. Однако не всякое сообщение содержит информацию. Информация - это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

В математической теории связи (теории информации) исходят из того, что в некотором сообщении xi количество информации I(xi) зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.

В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью p(xi). Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.

При определении количества информации исходят из следующих требований:

1. Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.

2. Количество информации о достоверном событии (p(xi)=1) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.

Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой

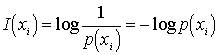. (1)

Чаще всего логарифм берется с основанием 2, реже - с основанием e:

двоичных единиц информации (бит),

натуральных единиц информации (нит).

Одну двоичную единицу информации содержит сообщение, вероятность выбора которого равняется 1/2. В этом случае

дв. ед. инф. (бит).

При применении натуральных логарифмов одну натуральную единицу информации содержит сообщение, вероятность выбора которого равняется 1/e:

нат. ед. инф. (нит).

Учитывая, что в практике передачи и преобразования информации широко применяются двоичные символы, двоичная логика, двоичные источники сообщений и двоичные каналы передачи, наиболее часто используется двоичная единица информации(бит).

Хотя при определении количества информации под сообщениями можно понимать любые фразы или телеграфные сообщения, мы здесь элементарными сообщениями будем называть отдельные буквы или слова. При использовании двухуровневых дискретных сигналов, например, мы будем пользоваться элементарными двоичными сигналами “1” и “0”, называя их буквами. Таким образом, алфавит двоичного источника состоит всего из двух букв, из которых можно строить более длинные комбинации, называемые кодовыми словами.

Вопросы

1. Что такое информация? Как определяется количество информации в сообщении?
2. Почему для определении количества информации в сообщении используется логарифмическая мера?
3. Какое сообщение содержит одну двоичную единицу информации?
4. Какое сообщение содержит одну натуральную единицу информации?

15. Энтропия дискретного источника с независимым выбором сообщений

В теории информации чаще всего необходимо знать не количество информации I(xi), содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.

Если имеется ансамбль (полная группа) из k сообщений x1, x2 ... xi, xk с вероятностями p(xi) ... p(xk), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений H(x), определяется формулой

(2) или (3)

Размерность энтропии - количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения.

Рассмотрим свойства энтропии.

1. Чем больше неопределённость выбора сообщений, тем больше энтропия. Неопределённость максимальна при равенстве вероятностей выбора каждого сообщения: p(x1)=p(x2)= . . .=p(xi)=1/k.

В этом случае

(4) (т.е. максимальная энтропия равна логарифму от объёма алфавита).

Например, при k=2 (двоичный источник) бит.

2. Неопределённость минимальна, если одна из вероятностей равна единице, а остальные - нулю (выбирается всегда только одно заранее известное сообщение, например, - одна буква): p(x1)=1; p(x2)= p(x3)= ... = p(xk)= 0. В этом случае H(x)=Hmin(x)=0.

Эти свойства энтропии иллюстрируются следующим образом.

Пусть имеется двоичный источник сообщений,

т.е. осуществляется выбор всего двух букв (k=2): x1 и x2, p(x1)+ p(x2)= 1. Тогда

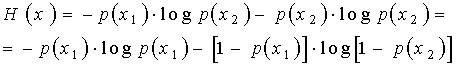(5)

Зависимость H(x) от вероятностей выбора для двоичного источника приведена на рис. 1.

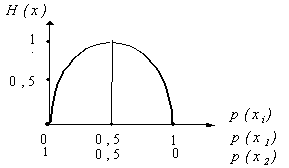
Рис. 1

3. Укрупним алфавит. Пусть на выходе двоичного источника имеется устройство, которое группирует буквы в слова из n букв. Тогда k = 2n слов (объём алфавита). В этом случае бит. (6)

Таким образом, укрупнение алфавита привело к увеличению энтропии в n раз, так как теперь уже слово включает в себя информацию n букв двоичного источника. Тем самым доказывается свойство аддитивности энтропии.

4. Энтропия дискретного источника не может быть отрицательной.

Термин “энтропия” заимствован из термодинамики и применительно к технике связи предложен американским учёным К.Шенноном, в трудах которого были заложены основы теории информации (математической теории связи).

Вопросы

1. Что такое энтропия источника с независимым выбором сообщений?
2. Как определяется энтропия дискретного источника с независимым выбором сообщений? Размерность энтропии источника.
3. Когда энтропия дискретного источника максимальна и чему она равна?
4. Когда энтропия дискретного источника минимальна (в частности, когда она равна нулю)?
5. Чему равна энтропия источника при укрупнении алфавита( при объединении букв в слова)?

16. Энтропия дискретного источника с зависимыми сообщениями

Ранее при определении энтропии предполагалось, что каждое сообщение (буква или слово) выбирается независимым образом. Рассмотрим более сложный случай, когда в источнике сообщений имеются корреляционные связи. В так называемом эргодическом источнике выбор очередной буквы сообщения зависит от конечного числа предшествующих букв n. Математической моделью такого источника является марковская цепь n-го порядка, у которой вероятность выбора очередной буквы зависит от n предшествующих букв и не зависит от более ранних, что можно записать в виде следующего равенства:

p(xi /xi-1,xi-2, ... xi-n)= p(xi /xi-1,xi-2, ... xi-n, ... xi-n-c), (7)

где с - произвольное положительное число.

Если объем алфавита источника равен k, а число связанных букв, которые необходимо учитывать при определении вероятности очередной буквы, равно порядку источника n, то каждой букве может предшествовать M=kn различных сочетаний букв (состояний источника), влияющих на вероятность появления очередной буквы xi на выходе источника. А вероятность появления в сообщении любой из k возможных букв определяется условной вероятностью (7) с учётом предшествующих букв, т.е. с учётом M возможных состояний. Эти состояния обозначим как q1, q2 ... qM.

Сказанное поясним двумя простыми примерами.

Пример 1. Пусть имеется двоичный источник (объём алфавита k=2) -например, источник, выдающий только буквы а и б ; порядок источника n=1. Тогда число состояний источника M=kn=21=2 (назовём их состояния q1 и q2). В этом случае вероятности появления букв а и б будут определяться следующими условными вероятностями:

p(а/q1=а), p(а/q2=б), p(б/q1=а), p(б/q2=б),

где q1=а - 1-е состояние q1,

q2=б - 2-е состояние q2.

Вероятности состояний источника равны p(q1)=p(a), p(q2)=p(б).

Пример 2. Пусть по-прежнему k=2 (буквы а и б), однако число связанных букв n=2. Тогда M=22=4 (4 возможных состояния: (а, а)=q1, (а, б)=q2, (б,а)=q3, (б, б)=q4 .

В этом случае имеем дело со следующими условными вероятностями:

p(а/а,а); p(а/а,б); p(а/б,а); p(а/б,б); p(б/а,а) . . . и т.д.

Вероятности состояний определяются равенствами p(q1)=p(a,a), p(q2)=p(a,б), p(q3)=p(б,a), p(q4)=p(б,б).

Энтропия эргодического дискретного источника определяется в два этапа.

1. Вычисляется энтропия источника в каждом из M состояний, считая эти состояния известными:

для состояния q1 ;

для состояния q2 ;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

для состояния qM .

2. Далее находим H(x) путём усреднения по всем состояниям q:

.

Окончательно получаем

. (8)

При наличии корреляционных связей между буквами в эргодическом источнике энтропия уменьшается, так как при этом уменьшается неопределённость выбора букв и в ряде случаев часть букв можно угадать по предыдущим или ближайшим буквам.

Вопросы

1. Что такое эргодический дискретный источник?
2. Что такое состояние эргодического дискретного источника, как вычислить количество состояний?
3. Как вычисляется энтропия эргодического источника?
4. Когда энтропия эргодического источника максимальна? Чему равен этот максимум?

17. Избыточность источника

Как было показано в разделах (2 и 3), энтропия максимальна при равновероятном выборе элементов сообщений и отсутствии корреляционных связей. При неравномерном распределении вероятностей и при наличии корреляционных связей между буквами энтропия уменьшается.

Чем ближе энтропия источника к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо использует источник свой алфавит, вводят понятие избыточности источника сообщений

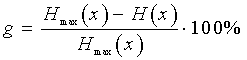(9)

или

.

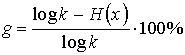Наличие избыточности приводит к загрузке канала связи передачей лишних букв сообщений, которые не несут информации ( их можно угадать и не передавая).

Однако, преднамеренная избыточность в сообщениях иногда используется для повышения достоверности передачи информации — например, при помехоустойчивом кодировании в системах передачи информации с исправлением ошибок. Большую избыточность имеет любой разговорный язык. Например, избыточность русского языка (как и других) - около 50%. Благодаря избыточности облегчается понимание речи при наличии дефектов в произношении или при искажениях речевых сигналов в каналах связи.

Вопросы

1. Что такое избыточность источника?
2. Какие факторы увеличивают избыточность источника?
3. Чему равна избыточность русского языка?
4. Большая избыточность – это хорошо или плохо для систем передачи информации по каналам связи?

18. Производительность источника

Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все элементы сообщения имеют одинаковую длительность t, то производительность

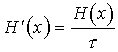. (10)

Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность , равную математическому ожиданию величины t :

.

Однако в последней формуле p(ti) можно заменить на p(xi) (вероятность i-го сообщения), так как эти вероятности равны. В результате получаем

, (11)

а производительность источника будет равна

. (12)

Mаксимально возможная производительность дискретного источника равна

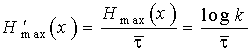. (13)

Для двоичного источника, имеющего одинаковую длительность элементов сообщения (k=2, ) имеем

бит¤с. (14)

При укрупнении алфавита в слова по n букв, когда k=2n, , имеем

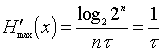бит¤с, что совпадает с формулой (14).

Таким образом, путём укрепления алфавита увеличить производительность источника нельзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз (n).

Увеличить производительность можно путём уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счет более экономного использования полосы пропускания, например, путем применения сложных многоуровневых сигналов.

Вопросы

1. Что такое производительность дискретного источника, чему она равна?
2. Когда производительность источника максимальна, чему она равна?
3. Можно ли увеличить производительность источника путём укрупнения алфавита?
4. Как можно увеличить производительность источника при заданной длительности элементов сообщения?

19. Совместная энтропия двух источников

Пусть имеется два дискретных источника с энтропиями H(x) и H(y) и объёмами алфавитов k и l (рис. 2).

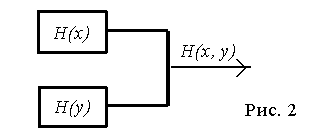
Объединим оба эти источника в один сложный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение xi и сообщение yj. Алфавит сложной системы будет иметь объём k×l, а энтропия будет равна

, (15)

или

. (16)

По теореме умножения вероятностей

p(x, y)=p(x)×p(y/x)=p(y)×p(x/y).

Подставляя эти соотношения в (15), получим

. (17)

Аналогично можно получить

. (18)

Здесь H(x) и H(y) - собственная энтропия источников x и y;

(19)

- условная энтропия источника y относительно источника x. Она показывает, какую энтропию имеют сообщения y, когда уже известно сообщение x.

Если источники независимы, то p(y/x)=p(y) и H(y/x)=H(y). В этом случае H(x, y)=H(x)+H(y).

Если источники частично зависимы, то H(x, y)<H(x)+H(y).

Если источники полностью зависимы (x и y - cодержат одну и ту же информацию), тоH(y/x)=0 и H(x, y)=H(x)=H(y).

Вопросы

1. Что такое совместная энтропия двух источников?
2. Что такое условная энтропия, её физический смысл?
3. Чему равна совместная энтропия двух независимых дискретных источников и двух полностью зависимых источников?

20. Взаимная информация источников сообщений

На рис. 3 показана условно собственная энтропия H(x) и H(y), условные энтропии H(x/y) иH(y/x) и совместная энтропия H(x, y). Из этого рисунка, в частности, следуют соотношения (17) и (18).

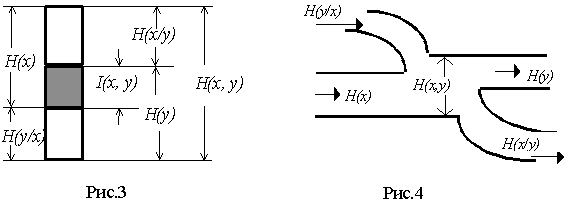
Часть рисунка, отмеченная штриховкой, называется взаимной информацией I(x, y). Она показывает, какое (в среднем) количество информации содержит сообщение x о сообщении y (или наоборот, сообщение y о сообщении x).

Как следует из рис. 3,

. (20)

Если сообщение x и y полностью независимы, то взаимная информация отсутствует и I(x, y)=0.

Если x и y полностью зависимы ( x и y - содержат одну и ту же информацию), то I(x, y)=H(x)=H(y).

Понятие взаимной информации очень широко используется в теории передачи информации. Требования к взаимной информации различны в зависимости от того, с какой информацией мы имеем дело. Например, если x и y - это сообщения, публикуемые различными газетами, то для получения возможно большей суммарной (совместной) информации взаимная (т.е. одинаковая в данном случае) информация должна быть минимальной. Если же x и y - это сообщения на входе и на выходе канала связи с помехами, то для получения возможно большей информации её получателем необходимо, чтобы взаимная информация была наибольшей. Тогда условная энтропия H(x/y) - это потери информации в канале связи (ненадежность канала), H(y/x) - это информация о помехах(энтропия источника помех - H(n)) , поступающая в канал извне или создаваемая внутренними помехами в канале (схематически этот процесс показан на рис.4).

Вопросы

1. Что такое взаимная информация двух источников ( или двух сообщений), чему она равна?
2. Что такое ненадежность канала передачи информации, как ее определить через условные вероятности?
3. Как определить информацию о помехах в канале передачи информации, используя условные вероятности перехода p(yj/xi)?

21. Скорость передачи и пропускная способность канала связи

В дискретной системе связи при отсутствии помех информация на выходе канала связи (канала ПИ) полностью совпадает с информацией на его входе, поэтому скорость передачи информации численно равна производительности источника сообщений:

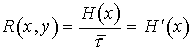. (21)

При наличии помех часть информации источника теряется и скорость передачи информации оказывается меньшей, чем производительность источника. Одновременно в сообщение на выходе канала добавляется информация о помехах (рис.5).

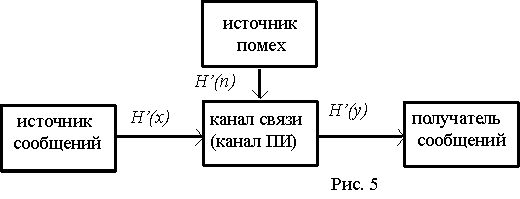
Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию:

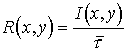бит/с. (22)

На основании формулы (20) имеем

или

, (23)

где H¢(x) - производительность источника;

H¢(x/y) - "ненадёжность" канала(потери) в единицу времени;

H¢(y) - энтропия выходного сообщения в единицу времени;

H¢(y/x)=H’(n) –энтропия помех ( шума) в единицу времени.

Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по каналу

. (24)

Для достижения максимума учитываются все возможные источники на выходе и все возможные способы кодирования.

Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согласованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.

В канале без помех C=max H¢(x), так как H¢(x/y)=0. При использовании равномерного кода с основанием k, состоящего из n элементов длительностью tэ, в канале без помех

,

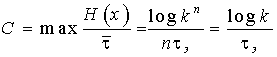при k=2 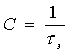бит/c. (25)

Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов связи без помех, так и для каналов с помехами на основании двух теорем, доказанных К.Шенноном.

1-ая теорема (для канала связи без помех):

Если источник сообщений имеет энтропию H (бит на символ), а канал связи – пропускную способность C (бит в секунду), то можно закодировать сообщения таким образом, чтобы передавать информацию по каналу со средней скоростью, сколь угодно близкой к величине C, но не превзойти её.

К.Шеннон предложил и метод такого кодирования, который получил название статистического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмена и в настоящее время широко используется на практике для “cжатия сообщений”.

2-ая теорема (для каналов связи с помехами):

Если пропускная способность канала равна C, а производительность источника H’(x)<C, то путём соответствующего кодирования можно передавать информацию по каналу связи со скоростью, сколь угодно к C и с вероятностью ошибки, сколь угодно близкой к нулю. Если же H’(x)>C, то можно закодировать источник таким образом, что ненадёжность будет меньше, чем H’(x)-C+e, где e. – сколь угодно малая величина.

Не существует способа кодирования, обеспечивающего ненадёжность, меньшую, чем H'(x)-C.

К сожалению, теорема К.Шеннона для каналов с шумами(помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако известно, что при приближении к пределу, устанавливаемому теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах кодирования и декодирования из-за увеличения длины кодового слова n. При этом вероятность ошибки на выходе канала стремится к величине

. (26)

Cледовательно, имеет место “обмен” верности передачи на скорость и задержку передачи.

Вопросы

1. Что такое пропускная способность канала связи, как она определяется?
2. Чему равна пропускная способность канала связи без помех?
3. Как влияют помехи на величину пропускной способности?
4. Что утверждает теорема Шеннона для канала связи без помех?
5. Что утверждает теорема Шеннона для канала связи с помехами?

22. Статистическое кодирование дискретных сообщений

Основой статистического (оптимального) кодирования сообщений является теорема К. Шеннона для каналов связи без помех.

Кодирование по методу Шеннона-Фано-Хаффмена называется оптимальным, так как при этом повышается производительность дискретного источника, и статистическим, так как для реализации оптимального кодирования необходимо учитывать вероятности появления на выходе источника каждого элемента сообщения ( учитывать статистику сообщений) .

Производительность и избыточность дискретного источника согласно определениям равны, соответственно,

, ;

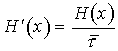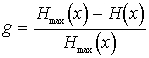откуда получаем

.

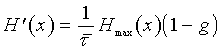Из этой формулы видно, что для увеличения производительности нужно уменьшать избыточность g и среднюю длительность сообщений .

Известно, что H(x)<Hmax(x), если априорные вероятности различных элементов сообщения различны (H(x)= Hmax(x) при равной вероятности этих элементов). Но при неравной вероятности сообщений можно применить оптимальное (статистическое) кодирование, при котором уменьшается средняя длительность сообщений.

Идея такого кодирования заключается в том, что, применяя неравномерный неприводимый код, наиболее часто встречающиеся сообщения (буквы или слова) кодируются короткими комбинациями этого кода, а редко встречающиеся сообщения кодируются более длительными комбинациями.

Рассмотрим принципы оптимального кодирования на приводимом ниже примере.

Пусть источник сообщений выдаёт 8 различных сообщений x1 ... x8 с вероятностями 0,495; 0,4; 0,026; 0,02; 0,018; 0,016; 0,015; 0,01 (сумма вероятностей равна 1).

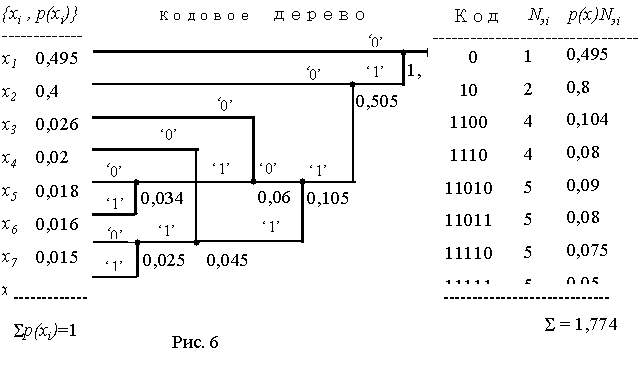
Располагаем эти сообщения столбцом в порядке убывания вероятностей (рис. 6). Объединяем два сообщения с самыми минимальными вероятностями двумя прямыми и в месте их соединения записываем суммарную вероятность: p(x7)+p(x8)=0,015+0,01=0,025. В дальнейшем полученное число 0,025 учитываем в последующих расчётах наравне с другими оставшимися числами, кроме чисел 0,015 и 0,01. Эти уже использованные числа из дальнейшего расчёта исключаются.

Далее таким же образом объединяются числа 0,018 и 0,016, получается число 0,034, затем вновь объединяются два минимальных числа (0,02 и 0,025) и т.д.

Построенное таким образом кодовое дерево используется для определённых кодовых комбинаций. Напомним, что для нахождения любой кодовой комбинации надо исходить их корня дерева (точка с вероятностью 1) и двигаться по ветвям дерева к соответствующим сообщениям x1 ... x8. При движении по верхней ветви элемент двоичного кода равен нулю, а при движении по нижней – равен единице. Например, сообщению x5 будет соответствовать комбинация 11010. Справа от кодового дерева записаны кодовые комбинации полученного неравномерного кода. В соответствии с поставленной задачей, наиболее часто встречающееся сообщение x1 (вероятность 0,495) имеет длительность в 1 элемент, а наиболее редко встречающиеся комбинации имеют длительность в 5 элементов. В двух последних столбцах рисунка приведено число элементов Nэi в кодовой комбинации и величина произведения p(xi)×Nэi , а представляет собой число элементов, приходящееся на одну комбинацию, т.е. в данном случае .

Если бы для кодирования был применён равномерный двоичный код, который чаще всего применяется на практике, число элементов в каждой кодовой комбинации для кодирования восьми различных сообщений равнялось бы трём (23=8), т.е. .

В рассматриваемом примере средняя длительность комбинаций благодаря применённому статистическому кодированию уменьшилась в 3/1,774=1,72 раза. Во столько же раз увеличилась и производительность источника (24).

Вопросы

1. Какая цель достигается при оптимальном кодировании дискретных сообщений?
2. Почему оптимальное кодирование называется оптимальным и почему статистическим?
3. В чём заключается идея оптимального кодирования?
4. Как осуществляется процесс кодирования дискретных сообщений оптимальным кодом по методу Шеннона - Фано - Хаффмена?
5. Почему код Шеннона - Фано должен быть неравномерным и неприводимым?

23. Статистическое кодирование кодовых слов

Дальнейшим развитием оптимального статистического кодирования является кодирование кодовых слов. В этом методе применяется также оптимальное кодирование по методу ШеннонаФаноХаффмена, однако не к отдельным буквам, а к кодовым словам (сочетаниям n букв первичного сообщения). Статистическое кодирование слов позволяет ещё больше уменьшить среднюю длительность сообщений, так как алфавит источника быстро увеличивается с увеличением длины слова. Число возможных кодовых слов (алфавит источника после объединения букв) определяется выражением m=kn, где k - алфавит букв первичного сообщения. Пусть, например, у нас имеется двоичный источник, дающий буквы а1 и а2 (например, “1” и “0”). При передаче этих букв по каналу связи используются сигналы длительностью tэ, а .

Рассмотрим пример, когда p(а1)=0,8 и p(а2)=0,2 (если вероятности p(а1) и p(а2) равны между собой, никакое кодирование не может уменьшить среднюю длительность сообщения). Образуем из элементов а1 и а2 слова из двух букв(n=2), беря различные сочетания из этих букв. Если у нас источник с независимым выбором элементов сообщений, то

p(а1а1)=0,8×0,8=0,64;

p(а1а2)= p(а2а1)=0,8×0,2=0,16;

p(а2а2)=0,2×0,2=0,04.

Применяя к полученным словам кодирование по методу ШеннонаФано, получаем кодовое дерево (рис. 7), из которого видно, что новые комбинации неравномерного кода имеют длительность tэ, 2tэ и 3tэ.

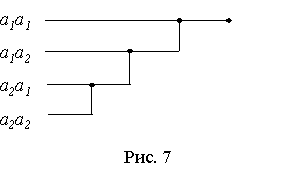
Средняя длина кодового слова

.

Но так как каждое слово содержит информацию о двух буквах первичного сообщения, то в расчёте на 1 букву получаем . Отсюда видно, что средняя длина элемента сообщения сократилась по сравнению с первоначальной в 1/0,78=1,38 раза.

Если усложнить кодирование и использовать n=3, то в этом случае получим . Это – уже почти предел, дальше уменьшать уже нецелесообразно. Чтобы убедиться в этом, рассчитаем производительность источника сообщений для всех трёх случаев.

Энтропия источника

.

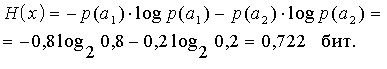При отсутствии статистического кодирования ,

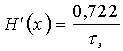бит/с.

При кодировании слов по две буквы ,

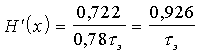бит/с.

При кодировании по две буквы

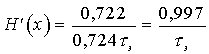бит/с.

Последняя величина близка к предельно возможной величине 1/tэ.

Статистическое кодирование слов целесообразно применять также в случае использования эргодического дискретного источника (источника с корреляционными связями букв), так как объединение букв в слова приводит к разрушению корреляционных связей (величина n должна быть не менее порядка эргодического источника, а n×tэ , соответственно, больше интервала корреляции букв первичного сообщения). Корреляционные связи между буквами трансформируются в различные вероятности появления возможных слов (n - буквенных сочетаний).

При этом необходимо помнить, что вероятность nбуквенных сочетаний определяется не произведением вероятностей отдельных букв, а, в соответствии с теоремой умножения, вероятностей надо учитывать также условные вероятности. Так, например, для источника с независимым выбором букв p(a1a1)=p(a1)×p(a1), а для эргодического источника с корреляционными связями букв p(a1a1)=p(a1)×p(a1/a1).

Вопросы

1. Какая цель достигается объединением букв в слова при оптимальном кодировании источников независимых сообщений?
2. Что является математической моделью источников сообщений с корреляционными связями?
3. Какая цель достигается объединением букв в слова при оптимальном кодировании источников зависимых сообщений, как выбирается длина кодовых слов?
4. Как осуществляется оптимальное кодирование сообщений с корреляционными связями?
5. В чём отличия алгоритмов оптимального кодирования кодовых слов для источников независимых и зависимых сообщений?

24. Пропускная способность однородного симметричного канала связи

В однородном канале связи условные(переходные) вероятности p(y1/x1) не зависят от времени. Граф состояний и переходов однородного двоичного канала связи приведен на рис. 8.

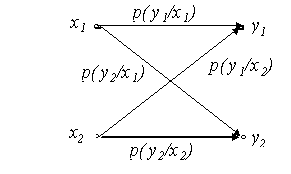
Рис.8

На этом рисунке x1 и x2 – сигналы на входе канала связи, y1 и y2 – сигналы на выходе. Если передавался сигнал x1 и принят сигнал y1, это означает, что первый сигнал (индекс 1) не исказился. Если передавался первый сигнал (x1), а принят второй сигнал (y2), это означает, что произошло искажение первого сигнала. Вероятности переходов указаны на рис. 7. Если канал симметричный, то вероятности переходов попарно равны.

Обозначим :

p(y2/x1)= p(y1/x2)=pэ – вероятности искажения элемента сигнала,

p(y1/x1)= p(y2/x2)=1-pэ – вероятности правильного приёма элемента сигнала.

В соответствии с формулами (21) и (23)

.

Если сигналы x1 и x2 имеют одинаковую длительность tэ, то . Тогда пропускная способность канала будет равна

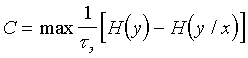. (27)

В этой формуле maxH(y)=logk. Для двоичного канала (k=2) maxH(y)=1 и формула (24) примет вид

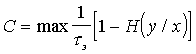. (28)

Остаётся определить условную энтропию H(y/x). В соответствии с (19) для двоичного источника имеем

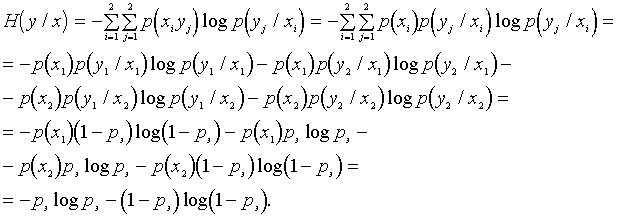
Подставив это значение условной энтропии в (28), получим окончательно

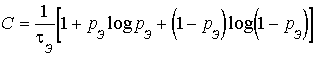. (29)

C, бит/с

Для канала связи с k>2 пропускная способность определяется почти аналогичной формулой:

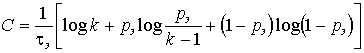. (30)

В заключении рассмотрим один пример. Пусть имеется двоичный источник с производительностью 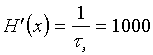бит/c.

Если вероятность искажения pэ=0,01, то из этого следует, что из 1000 элементов сигнала, переданных за одну секунду, в среднем 990 элементов будут приняты без искажений и только 10 элементов будут искажены. Казалось бы, пропускная способность в этом случае будет составлять 990 бит в секунду. Однако вычисление по формуле (29) даёт нам величину, значительно меньшую (C=919 бит/с). В чём здесь дело? А дело в том, что мы получили бы C=990 бит/с, если бы точно знали, какие именно элементы сообщения искажены. Незнание этого факта (а это практически знать невозможно) приводит к тому, что 10 искажённых элементов настолько сильно снижают ценность принимаемого сообщения, что пропускная способность резко уменьшается.

Другой пример. Если pэ=0,5, то из 1000 переданных элементов 500 не будут искажены. Однако теперь уже пропускная способность будет составлять не 500 бит/с, как можно было бы предполагать, а формула (29) даст нам величину C=0. Действительно при pэ=0,5 сигнал по каналу связи фактически уже не проходит и канал связи просто эквивалентен генератору шума.

При pэ>1 пропускная способность приближается к максимальной величине. Однако в этом случае сигналы на выходе системы связи необходимо инвертировать.

Вопросы

1. От чего зависит пропускная способность дискретного канала связи с помехами?
2. Как определяется пропускная способность дискретного канала связи с помехами?
3. Как влияют помехи на величину пропускной способности канала связи?
4. Чему равна пропускная способность двоичного канала связи при вероятности искажения элемента сообщения, равной 0,5?

25. Энтропия непрерывной случайной величины и её свойства

Энтропия дискретного случайного сигнала определяется выражением (2). Для непрерывной случайной величины воспользуемся этим же выражением, заменив вероятность p(x) на w(x)dx.

В результате получим

.

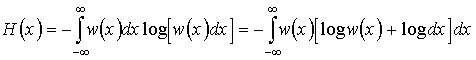Но логарифм бесконечно малой величины (dx) равен минус бесконечности, в результате чего получаем

.

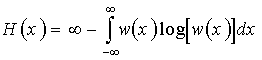Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но так как в последнем выражении первое слагаемое (¥) от величины x или от w(x) не зависит, при определении энтропии непрерывной величины это слагаемое отбрасывают, учитывая только второе слагаемое (некоторую “добавку” к бесконечности). Эта добавочная энтропия, определяемая формулой

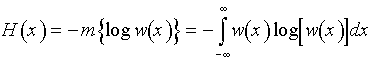(31)

-называется дифференциальной энтропией непрерывной случайной величины.

В дальнейшем слово “дифференциальная” в определении энтропии будем иногда опускать.

Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины.

1. Условная энтропия случайной величины y относительно случайной величины x.

, или

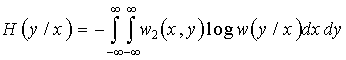. (32)

2. Совместная энтропия двух непрерывных случайных величин равна

, или 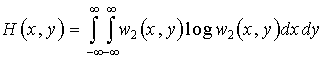. (33)

Для независимых x и y H(x,y)=H(x)+H(y).

Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (17) и (18).

3. Взаимная информация I(x,y), содержащаяся в двух непрерывных сигналах x и y, определяется формулой (16).

Для независимых x и y взаимная информация I(x,y)=0.

4. Если случайная величина ограничена в объёме V=b-a, то её дифференциальная энтропия максимальна при равномерном закона распределения этой величины (рис. 10).

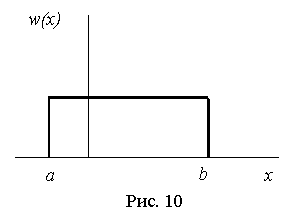
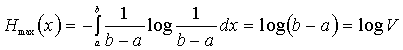. (34)

Так как эта величина зависит только от разности (b-a), а не от абсолютных величин b и a, следовательно, Hmax(x) не зависит от математического ожидания случайной величины x.

5. Если случайная величина не ограничена в объёме (т.е. может изменяться в пределах от -¥ до +¥), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Определим этот максимум.

В соответствии с (31)

;

.

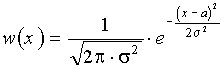Отсюда

.

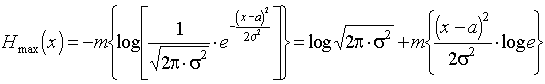Но математическое ожидание m{(x-a2)}=s2, отсюда получаем

,

или окончательно

. (35)

Cледовательно, энтропия зависит только от мощности s2.

Эта очень важная формула будет использоваться позднее для определения пропускной способности непрерывного канала связи.

Заметим, что, как и ранее, Hmax(x) не зависит от математического ожидания a случайной величины x. Это важное свойство энтропии. Оно объясняется тем, что математическое ожидание является не случайной величиной.

Вопросы

1. Как определяется дифференциальная энтропия непрерывной случайной величины? Разновидности энтропии непрерывной случайной величины.
2. Чему равна максимальная дифференциальная энтропия, если случайная величина ограничена в объёме, при каком законе распределения она максимальна?
3. Чему равна максимальная дифференциальная энтропия, если случайная величина не ограничена в объёме?
4. Как влияет математическое ожидание случайной величины на её энтропию?

26. Энтропия и производительность эргодического источника непрерывного сигнала

Сигнал, отображающий непрерывное сообщение, можно рассматривать как некоторый эргодический случайный процесс, спектр которого ограничен полосой частот. В соответствии с теоремой Котельникова для описания этого процесса длительностью T требуется отсчётов, где 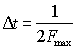– интервал Котельникова. Так как сигнал с ограниченным спектром полностью характеризуется своими отсчётными значениями, то знание значений сигнала между отсчётами не увеличивают наших знаний о сигнале. Следовательно, при определении энтропии непрерывного сигнала достаточно учитывать только его отсчётные значения.

Известно, что энтропия обладает свойством аддитивности. Так, если у какого‑то дискретного сигнала длительностью t энтропия равна H(x), то энтропия сигнала, составленного из N элементов, будет равна N×H(x). Аналогичным образом можно вычислить энтропию непрерывного сигнала длительностью T, которая будет равна

,

где H1(x) – энтропия одного сечения случайного сигнала, определяемая по формуле (28) через одномерную плотность вероятности. Размерность энтропии H1(x) – бит на один отсчёт случайного сигнала (одно сечение случайного процесса).

Производительность непрерывного случайного процесса будет равна

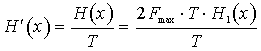
или

бит/с. (36)

Таким образом, производительность эргодического источника непрерывного сигнала полностью определяется энтропией одного отсчета и удвоенной полосой частот этого сигнала.

Вопросы

1. Что такое энтропия непрерывного случайного процесса?
2. Как в энтропии проявляется свойство эргодичности случайного процесса?
3. Как определяется энтропия непрерывного эргодического случайного процесса, её размерность?
4. Как определяется производительность непрерывного эргодического случайного процесса, её размерность?

27. Пропускная способность непрерывного канала связи

Если x(t) – сигнал на входе канала связи, а y(t)=x(t)+n(t) – сигнал на его выходе (n(t) – аддитивная помеха), то скорость передачи информации по непрерывному каналу связи будет определяться выражением (23), в котором величину 1/t надо заменить на 2Fmax (или 2Fk, предполагая, что источник сигнала согласован с каналом и его полоса пропускания Fk= Fmax)

, (37)

где, как и ранее, H(y) – это энтропия выходного сообщения, H(y/x) – энтропия шума (почему она так называется, будет видно из дальнейшего изложения).

Пропускная способность равна максимально возможной скорости передачи по каналу связи, когда источник сигнала полностью согласован с характеристиками канала связи:

. (38)

Максимум H(y) достигается в случае гауссовского закона распределения случайной величины y. При этом

. (39)

При учёте влияния помехи необходимо рассматривать наихудший случай, когда помеха распределена также по гауссовскому закону.

Условная вероятность w(y/x) – это попросту вероятность распределения случайной величины y при якобы известном заранее значении x, хотя величина x является случайной. Но, так как y(t)=x(t)+n(t), можно записать

,

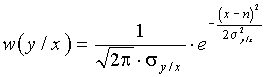где s2y/x – дисперсия величины y при известном x, т.е. дисперсия помехи s2n.

Определим условную энтропию H(y/x)

.

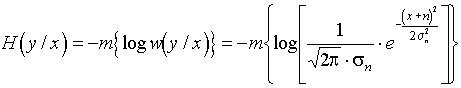В этом выражении предполагается, что x известно заранее. Таким образом, величина x в приведенном выражении является попросту математическим ожиданием величины y. Однако известно, что энтропия непрерывного случайного процесса от математического ожидания не зависит.

Тогда получаем, что

.

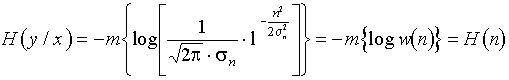Отсюда видно, почему условная энтропия H(y/x) называется энтропией шума.

Для гауссовского закона распределения помехи максимальное значение энтропии шума, в соответствии с (35), будет равно

. (40)

Подставляя (39) и (40) в (38), получаем .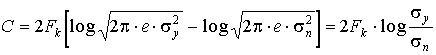

Перенося число 2 под знак логарифма, получим 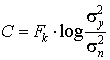. В этом выражении s2n=Pп – мощность помехи, а s2y=s2x+s2n=Pс+Pп, где Pс – мощность сигнала на выходе канала связи. С учётом этого получаем окончательно формулу для вычисления пропускной способности непрерывного канала связи (формулу Шеннона):

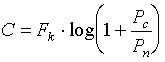. (41)

В заключение можно отметить следующее.

Для достижения скорости передачи информации по непрерывному каналу связи, близкой к пропускной способности канала связи, сигнал x(t) по статистической структуре должен быть близок к флюктуационной помехе (белому шуму) с гауссовским законом распределения.

Вопросы

1. От чего зависит пропускная способность непрерывного канала связи?
2. Приведите формулу для нахождения пропускной способности непрерывного канала связи.
3. Как изменяется пропускная способность непрерывного канала связи при увеличении эффективной полосы пропускания канала?
4. Какие предъявляются требования к сигналу (его статистической структуре), чтобы приблизить скорость передачи непрерывного сигнала к пропускной способности канала?

28. Эпсилон-энтропия источника непрерывных сообщений

Сигнал на выходе источника (И) рис.11 непрерывных сообщений (например, микрофона, телефона, датчика температуры и пр.) представляет собой непрерывный случайный процесс, энтропия которого в любом из сечений в общем случае равна бесконечности как это было показано в разделе 12. Такое количество информации не может быть передано по реальному каналу связи, пропускная способность которого всегда ограничена. Это и не нужно, так как скорость восприятия информации любым потребителем на выходе канала всегда ограничена его физическими возможностями. Поэтому непрерывный сигнал на выходе канала связи даже без помех отличается от сигнала на входе, так как содержит не всю информацию о нем (причем под каналом связи можно понимать любое преобразование одного ансамбля сигналов в другое: модуляцию, усиление, дискретизацию и пр.). Уже преобразование непрерывного сообщения в сигнал соответствующим устройством (микрофоном или др. датчиком сигнала) связано с потерей части информации, а сигнал отображает сообщение лишь с некоторой точностью

e(t)= x(t)- x*(t),

где x(t) - сигнал на входе преобразователя;

x*(t) - сигнал на выходе преобразователя(Пр) или оценка входного сигнала преобразователем, который всегда представляет собой некоторое решающее устройство, работающее по определенному правилу и заданному критерию качества.

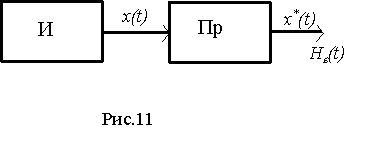
Критерий качества, как известно, определяется потребителем информации, например, среднеквадратическое отклонение

eср=m{[ x(t)- x*(t)]2} , (42)

или дисперсия ошибки

.

Эпсилон-энтропией He(x)( e- энтропией) называется минимальное количество информации, которое должно содержаться в выходном сигнале x*(t) о входном сигнале x(t), чтобы этот сигнал можно было восстановить с заданной точностью eср.

He(x)=min I(x,x*)=H(x)- max H(x/x*), (43)

где

I(x,x*)-взаимная информация x и x* ;

H(x) и H(x/x*)- соответственно, дифференциальная энтропия сигнала x(t) и условная энтропия x(t), когда x*(t) известно;

min и max берутся по всевозможным условным распределениям w(x/x*).

В общем случае, когда сигнал (или сообщение) x(t) является гауссовским с дисперсией , ошибка e(t) также является гауссовской с дисперсией , а с учетом аддитивного характера ошибки e(t) условная энтропия H(x/x*) полностью определяется дифференциальной энтропией H(e). Соответственно, max H(x/x*)= max H(e)= .

Тогда e- энтропия одного сечения гауссовского источника (e- энтропия одного отсчета)

He(x)= - = 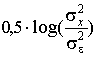. (44)

Величина показывает отношение мощности(дисперсии) сигнала x(t) к мощности (дисперсии) ошибки, при котором среднеквадратическое отклонение сигналов x(t) и x*(t) не превышает se.

Следовательно, производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передавать в единицу времени, чтобы восстановить сообщение с заданной точностью.

H’e(x)=v× He(x), (45)

где v=1/Dt - скорость передачи отсчетов на выходе источника, Dt - интервал между отсчетами.

Для стационарного сигнала с ограниченным спектром Dt=1/(2Fmax), тогда H’e(x)= 2Fmax × He(x).

Если, кроме того, источник является гауссовским, то

H’e(x)= Fmax 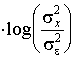. (46)

Количество информации, выдаваемое гауссовским источником за время Tc , равно Tc × H’e(x)= Tc × Fmax 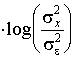, (47)

что совпадает с формулой для объёма сигнала, когда динамический диапазон сигнала Dc= .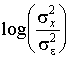

Это значит, что объем сигнала на выходе источника равен количеству информации (46), которое содержится в сигнале для его воспроизведения с заданной точностью.

Для канала с пропускной способностью С, на входе которого подключен источник с производительностью H’e(x), теорема К.Шеннона для канала с шумами принимает вид:

Если при заданном критерии точности источника (например,se) его эпсилон- производительность меньше пропускной способности канала H’e(x)< С, то существует способ кодирования (преобразования сигнала), при котором неточность воспроизведения сколь угодно близка к se; при H’e(x)> С такого способа не существует.

Теорема К.Шеннона определяет предельные возможности согласования источника непрерывных сообщений с каналом связи. Практически это достигается применением помехоустойчивых видов модуляции и кодирования.

Вопросы

1. Что такое эпсилон-энтропия?
2. Как вычисляется эпсилон -энтропия источника непрерывных сигналов?
3. Как определяется эпсилон -производительность источника стационарных сигналов?
4. Как определяется эпсилон- энтропия и производительность гауссовского источника?
5. Что утверждает теорема Шеннона для канала связи, на входе которого подключен источник с известной эпсилон- производительностью?

29. Обмен мощности сигнала на ширину его спектра

Из выражения (41) может создаться ошибочное впечатление, что пропускная способность непрерывного канала связи может неограниченно возрастать при увеличении Fk. Однако это не верно, так как с увеличением Fk растёт мощность флюктуационной помехи, а величина Pп стоит в знаменателе под знаком логарифма в выражении (41).

Мощность помехи

, (48)

где N0 – спектральная плотность мощности помехи.

Подставив это в (41), получим

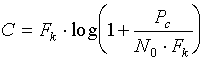. (49)

Анализ полученного выражения показывает, что при увеличении полосы пропускания пропускная способность стремится к некоторому пределу, а не растёт бесконечно (рис.12).

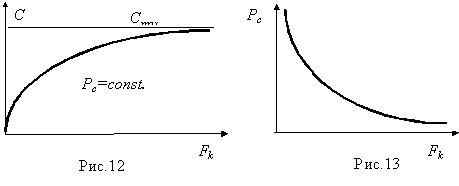
Несколько другой результат получается при рассмотрении зависимости необходимой мощности сигнала от Fk – при заданной пропускной способности C и спектральной плотности помехи N0. Преобразуя выражение (43), получим

.

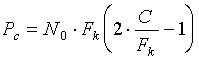Эта зависимость изображена на рис. 13, из которого видно, что необходимая мощность сигнала Pс при увеличении Fk монотонно убывает. Это позволяет передавать с необходимой скоростью информацию на очень большие расстояния с очень малой мощностью сигнала, если только применить достаточно широкополосные сигналы.

Возможность уменьшения мощности сигнала за счёт увеличения полосы частот называется обменом мощности сигнала на полосу частот. Эта возможность часто учитывают при разработке систем космической связи, когда мощность сигнала ограничена мощностью источников питания космических аппаратов.

Вопросы

1. Что такое обмен мощности сигнала на полосу частот?
2. Каким образом можно уменьшить мощность сигнала при заданной пропускной способности канала в случае передачи сигналов на большие расстояния?

30. Сравнение пропускной способности непрерывного и дискретного каналов связи

Пропускная способность двоичного дискретного канала связи определяется формулой (29). В настоящее время в двоичном канале связи скорость передачи символов v может достигать значения 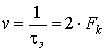. В связи с этим формула (29) может быть переписана в следующем виде:

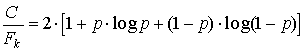. (50)

Для определённости будем считать, что в дискретном канале передача ведётся методом дискретной частотной модуляции, в этом случае вероятность ошибки определяется известной формулой

.

Подставив это выражение в формулу (50), получим зависимость пропускной способности дискретного двоичного канала связи от величины h (рис.14 - кривая 1). Из этого рисунка видно, что при h®¥ пропускная способность двоичного канала стремится к ( 2 × Fk × log2k).

Пропускная способность непрерывного канала связи определяется формулой Шеннона ( 41), откуда получаем

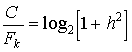. (51)

Эта зависимость также приведена также на рис. 14 (кривая 2).

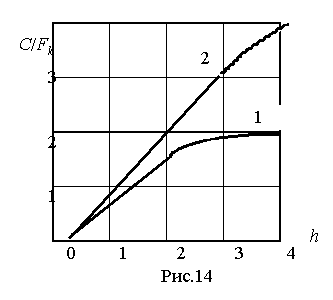
Сравнивая оба графика, видим, что при стремлении h к бесконечности для дискретного канала связи отношение C/Fk стремится к пределу (равному двум), а для непрерывного канала связи C/Fk неограниченно растёт, причём для любого значения h пропускная способность непрерывного канала связи превышает пропускную способность дискретного канала. Это объясняется тем, что сигналы дискретной модуляции отличаются от белого гауссовского шума, а согласно теореме Шеннона, наибольшей пропускной способностью обладают системы, в которых сигналы близки к белому гауссовскому шуму. Непрерывные сигналы по своей структуре ближе к гауссовскому шуму, чем дискретные сигналы.

Вопросы

1. Как изменяется пропускная способность дискретного канала связи при увеличении мощности сигнала?
2. Как изменяется пропускная способность непрерывного канала связи при увеличении мощности сигнала?
3. Почему пропускная способность непрерывного канала выше, чем пропускная способность дискретных каналов при любых значениях h > 0?

31. Эффективность систем связи

Термин ”эффективность” означает ”экономичность”. Эффективность можно оценивать в денежных единицах (стоимость строительства канало-километра линии связи, срок окупаемости, эксплутационные расходы и т.д.). Хотя это – важные показатели эффективности, мы будем определять эффективность систем связи, пользуясь их техническими характеристиками. Например, если какая-то система связи обеспечивает передачу информации по каналу тональной частоты со скоростью 1200 бит/с, а вторая система со скоростью 9600 бит/с, с нашей точки зрения вторая система считается более эффективной (с точки зрения использования пропускной способности канала связи), однако стоимость второй системы может быть более высокой, чем первой. Да и с точки зрения технических показателей вторая система может считаться менее эффективной, чем первая, если сравнение производить не по пропускной способности канала (или полосе частот канала связи), а, например, по мощности сигнала, передаваемого по линии связи. Во втором случае может потребоваться большая мощность сигнала и с этой точки зрения вторая система может оказаться менее эффективной и с точки зрения её технических показателей.

Современные системы связи должны обеспечивать достаточно высокую скорость передачи информации при заданной полосе частот, минимальной мощности сигнала и минимальной вероятности искажений.

Для оценки эффективности систем связи наиболее часто пользуются тремя показателями эффективности: это b - эффективность, g - эффективность, h - эффективность, определяемые формулами:

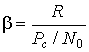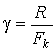, , , (52)

В этих формулах: R – скорость передачи информации; Pc / N0 – отношение мощности сигнала к спектральной плотности мощности помехи;

Fk – полоса пропускания канала связи; C – пропускная способность канала связи.

Все перечисленные показатели эффективности являются безразмерными величинами и определяются в предположении, что в канале связи обеспечивается достаточно малая (заранее заданная) вероятность искажения сигналов (при передаче дискретных сигналов) или заданное отношение мощности сигнала к мощности помехи (при передаче непрерывных сигналов).

Приведённые выше показатели имеют простой физический смысл. b - эффективность показывает, как используется мощность сигнала при передаче информации с заданной скоростью R, g - эффективность показывает, как используется полоса частот канала связи, h - эффективность показывает, как используется пропускная способность канала связи.

Все показатели эффективности взаимосвязаны. Для определения этой взаимосвязи исключим из формул (52) величину R, в результате чего получим

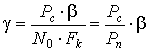, (53)

где 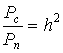– отношение мощности сигнала к мощности помехи.

От величины h2 зависит пропускная способность непрерывного (гауссовского) канала связи, определяемая формулой Шеннона (41). Подставляя в эту формулу соотношения (52) и (53), получим

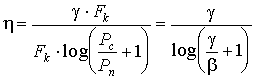. (54)

Рассмотрим предельную зависимость между b и g, которую получим из (54), положив h =1 (теоретически предельно достижимая величина – согласно теореме Шеннона для канала, в котором сигнал и помеха по своей структуре близки к белому гауссовскому шуму, величина R может быть сколь угодно близка к C при соответствующем кодировании сигнала). В результате простых преобразований получаем

. (55)

Полученная предельная зависимость между b и g для непрерывного канала приведена на рис. 15 (величины b и g откладываются на этом рисунке в логарифмическом масштабе).

Представляет интерес найти значения b и g для различных видов дискретной модуляции. При расчёте этих величин будем считать, что вероятность искажения сигналов очень мала (положим, вероятность искажения элементарного сигнала pэ= 10-5). В этом случае, если воспользоваться формулой (29), получаем, что R » C = 1/Т, где Т – длительность элементарного сигнала.

Эффективная полоса частот канала связи для разных видов модуляции определяется формулами:

Fk - для двухпозиционной АМ;

Fk 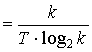- для ЧМ;

Fk 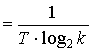- для ФМ и ОФМ. (56)

Определим величину b для рассматриваемого случая(малой вероятности искажения сигналов).

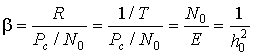, (57)

где Е = Рс×Т – энергия сигнала.

Величину h02 найдём для случая заданной вероятности ошибок pэ = 10-5 при оптимальном приёме сигналов АМ, ЧМ, ФМ из формул:

pошАМ ;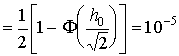

рошЧМ ;

рошФМ , (58)

откуда h02АМ =39 ; h02ЧМ =19,5; h02ФМ =9,75.

Все вычисления для случая использования двухпозиционных сигналов приведены в таблице 1. Там же приведены значения h – эффективности, определяемой формулой (54).

Полученные значения h – эффективности показывают, какая была бы h – эффективность, если бы при рассчитанных значениях b и g информация передавалась бы непрерывными сигналами.

Приведённые вычисления можно продолжить для случаев использования многопозиционных сигналов. Результаты вычислений приведены в виде кривых на рис.15 для сигналов АМ, ЧМ, ФМ, ОФМ. Цифры на этих кривых указывают на число позиций используемых сигналов.

Таблица 1. Вычисление коэффициентов b и g для двухпозиционных сигналов

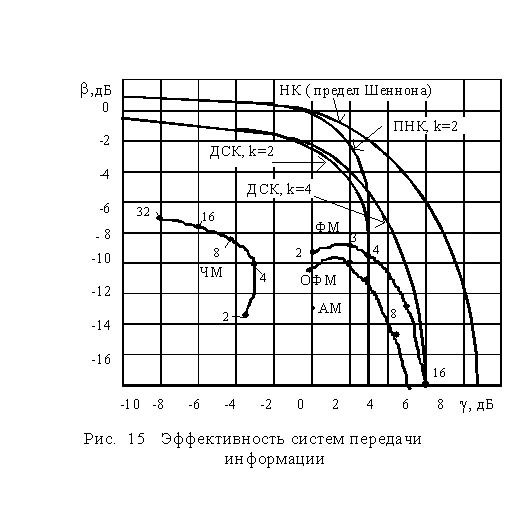
Относительно b эффективности при АМ необходимо сделать одно уточнение. Дело в том, что сигналы АМ, в отличие от сигналов ЧМ и ФМ, имеют “пассивную” паузу (при передаче сигнала “0” мгновенная мощность сигнала равна нулю). С учетом этого обстоятельства, т.е. при учете средней мощности сигнала АМ, а не пиковой, величина b увеличивается на 3 дБ. Это обстоятельство учтено на рис.15.

Из рисунка видно, что при увеличении позиций кода в случае ЧМ величина b растёт, а g – убывает, т. е. в случае ЧМ улучшается использование мощности сигнала, но ухудшается использование полосы частот. Следовательно, многопозиционную ЧМ целесообразно применять в тех случаях, когда ограничена энергетика линии связи — например, в системах космической связи; полоса частот, занимаемая сигналом, в этих системах почти не лимитируется. И наоборот, для сигналов ФМ с ростом числа позиций применяемого сигнала g - эффективность возрастает, а b - эффективность — уменьшается. Такие сигналы целесообразно использовать в системах с ограниченной полосой частот — например, в системах многоканальной телефонной связи с ИКМ.

На рис. 15 приведены также кривые для систем с дискретными сигналами (k =2), использующих оптимальную обработку сигналов в полунепрерывном канале (ПНК ) и для систем с дискретными сигналами (k =2 и k =4), использующих обработку сигналов в дискретном канале. Из рисунка видно, что эти системы по своей эффективности ближе к пределу Шеннона при ограничении g из-за дискретности сигналов

g max=Rmax /F = log k / TF. (59)

Отличие систем с ПНК и ДСК по b - эффективности определяется тем, что в системах с ПНК оптимальная обработка кодовых слов реализуется в непрерывном канале (прием в целом); в системах с ДСК оптимальная обработка сигналов производится по элементам кода в непрерывном канале (поэлементный прием), а оптимальное декодирование кодовых слов - в дискретном канале. Предполагается, что и в том и в другом случае используется помехоустойчивое кодирование в соответствии с теоремой Шеннона для каналов с помехами.

Вопросы

1. Что такое эффективность систем связи?
2. Что такое бета – эффективность?
3. Что такое гамма – эффективность?
4. Что такое эта – эффективность?
5. Какой вид дискретной модуляции целесообразно использовать в системах связи при ограниченной мощности сигнала и при ограниченной полосе частот?
6. Какие системы связи по эффективности ближе к пределу, определяемому формулой Шеннона?

Список литературы

1-12. Основы теории помехоустойчивости дискретных сигналов

1. В.А. Котельников. Теория потенциальной помехоустойчивости. -- М. , Госэнергоиздат , 1956.

2. Основы теории передачи сигналов, часть 2 / Б.Н.Бондарев, А.А.Макаров: Учебное пособие. - Новосибирск, НЭИС, 1969. -140с.

3. Теория передачи сигналов: Учебник для вузов/ А.Г.Зюко, Д.Д.Кловский, М.В.Назаров, Л.М.Финк. -М.: Радио и связь, 1986. -304с.

14-31. Основы теории передачи информации

1. Теория передачи сигналов: Учебник для вузов/ А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк.- 2 -ое изд., перераб. и доп. - М.: Радио и связь, 1986. - 304с.

2. Бондарев Б.Н., Макаров А.А. Основы теории передачи сигналов: Учебное пособие. - Новосибирск: НЭИС, 1970. - 132с.

3. Теория передачи сигналов: Учебник для вузов/ М.В. Назаров, Б.И. Кувшинов, О.В. Попов. - М.: Связь, 1970. - 368с.